Течение газа в ступени турбомашины
ГЛАВА ДЕВЯТАЯ
ТЕЧЕНИЕ ГАЗА В СТУПЕНИ ТУРБОМАШИНЫ
9-1. ОСНОВНЫЕ УРАВНЕНИЯ
В ступени турбомашиньи происходит преобразование потенциальной энергии газа в механическую работу (турбина) или механической работы в потенциальную энергию газа (компрессор). В обоих случаях поток газа совершает энергетический обмен с окружающей средой.
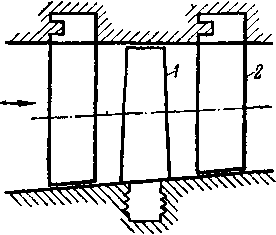
Рассмотрим принципиальную схему ступени турбины с осевым потоком газа. На рис. 9-1 показаны основные элементы такой ступени. По входному патрубку 1 газ подводится к неподвижной направляющей решетке 2, где часть его потенциальной энергии преобразуется в кинетическую энергию. Приобретая в направляющей решетке значительные скорости, поток газа проходит через зазор 3 и попадает на рабочие лопатки 4, укрепленные на колесе 5. Здесь происходит перенос энергии к ротору турбины.
Радиусами г и r+dr проведем два цилиндрических сечения, ось которых будет совпадать с осью турбины. Этими сечениями выделим элементарную ступень турбины; развертывая ее на плоскость (рис. 9-2,а), можно проследить характер изменения скоростей в проточной части ступени114.
Введем в отличие от предыдущего следующие обозначения скоростей:
с — скорость абсолютного движения газа; скорость газа в относительном движении;
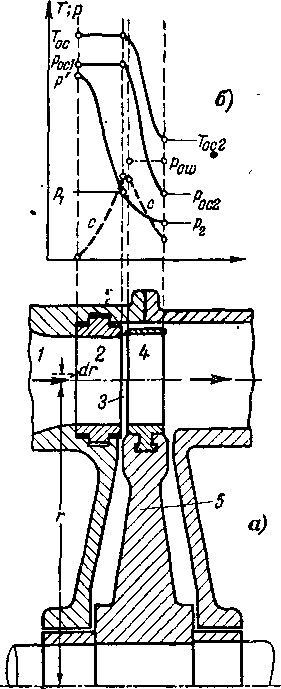
Рис. 9-1. Схема ступени турбины в осевом потоке газа (а) и распределение параметров торможения, статических давлений и скоростей •в проточной части (б).
w
¦ скорость переносного движения (окружная скорость); и wи — проекции ско
a -
ростей абсолютного и относительного потоков на направление скорости и;
- проекции скоростей абсолютного и относительного потоков на направление оси вращения;
W
.,w — радиальные составляющие скоростей абсолютного и относительного потоков.
Индексом 1 обозначим скорости, относящиеся ко
входу, a индек!сол^ 2 — к выходу из рабочих лопаток.
Рабочий процесс ступени турбины можно (проследить по рис. 9-1 и 9-2. В межлопаточных каналах направляющей решетки поток газа ускоряется и одновременно поворачивается, покидая ее со скоростью с\, направленной под углом си к оси решетки (рис. 9-2,а). При этом ло-6П2.2 Дейч Михаил Ефимович
Д 27 Техническая газодинамика. Изд. 2-е, переработ. М.—Л.
Госэнергоиздат, 1961
с черт. и илл. 6П2.2
design pashaok
Редактор Б. Я¦ Шумяцкий Техн. редактор А. М. Фридкин
ГЛАВА ДЕВЯТАЯ
ТЕЧЕНИЕ ГАЗА В СТУПЕНИ ТУРБОМАШИНЫ
9-1. ОСНОВНЫЕ УРАВНЕНИЯ
В ступени турбомашиньи происходит преобразование потенциальной энергии газа в механическую работу (турбина) или механической работы в потенциальную энергию газа (компрессор). В обоих случаях поток газа совершает энергетический обмен с окружающей средой.
Рассмотрим принципиальную схему ступени турбины с осевым потоком газа. На рис. 9-1 показаны основные элементы такой ступени. По входному патрубку 1 газ подводится к неподвижной направляющей решетке 2, где часть его потенциальной энергии преобразуется в кинетическую энергию. Приобретая в направляющей решетке значительные скорости, поток газа проходит через зазор 3 и попадает на рабочие лопатки 4, укрепленные на колесе 5. Здесь происходит перенос энергии к ротору турбины.
Радиусами г и r+dr проведем два цилиндрических сечения, ось которых будет совпадать с осью турбины. Этими сечениями выделим элементарную ступень турби-ньи; развертывая ее на плоскость (рис. 9-2,а), можно проследить характер изменения скоростей в проточной части ступени115.
Введем в отличие от предыдущего следующие обозначения скоростей:
с — скорость абсолютного движения газа; w — скорость газа в относительном движении; и — скорость переносного движения (окружная скорость); проекции скоростей абсолютного и относительного потоков на направление скорости и;
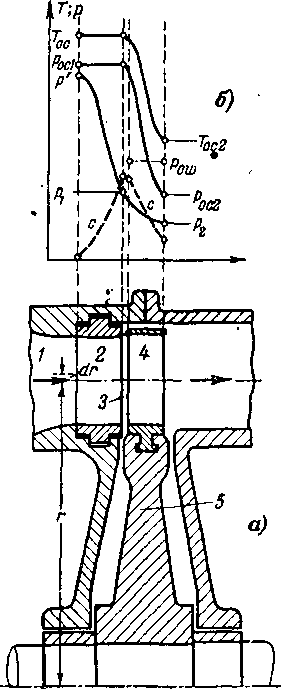
Рис. 9-1. Схема ступени турбины в осевом потоке газа (а) и распределение параметров торможения, статических давлений н скоростей ¦в проточной части (б).
си И W
проекции скоростей абсолютного и относительного потоков на направление оси вращения;
W
радиальные составляющие скоростей абсолютного и относительного потоков.
W
Индексом 1 обозначим скорости, относящиеся ко
входу, а индекйоА^ 2 — к выходу из рабочих лопаток.
Рабочий процесс ступени турбины можно проследить по рис. 9-1 и 9-2. В межлопаточных каналах направляющей решетки поток газа ускоряется и одновременно поворачивается, покидая ее со скоростью сь направленной под углом си к оси решетки (рис. 9-2,а). При этом ло-генциальная энергия газа преобразуется в кинетическую энергию потока.
На рабочие лопатки поток входит с относительной скоростью wI, которую легко получить, ‘построив входной треугольник скоростей.
В межлопаточных каналах рабочей решетки происходи? поворот потока в относительном движении; при
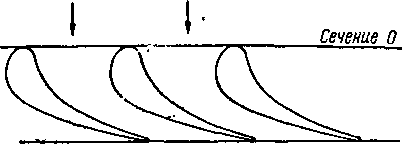
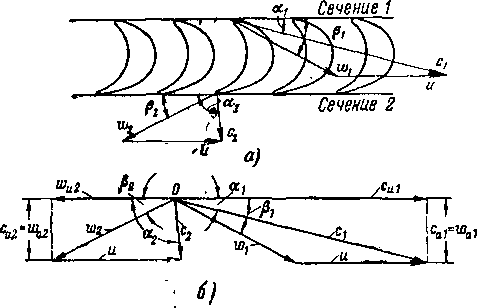
Рис. 9-2. Развертка проточной части (а) и треугольники скоростей осевой ступени (б).
этом силы давления газа производят работу вращения ротора турбины. Поток выходит из рабочих лопаток с относительной скоростью w2 под углом Рг к оси решетки. Зная окружную скорость и, легко построить выходной треугольник скоростей и определить скорость абсолютного потока на выходе из ступени с2 (рис. 9-2,а). Часто входной и выходной треугольники скоростей изображают из одного полюса, как показано на рис. 9-2,6.
Таким образом, энергия газа передается к ротору турбины благодаря тому, что силы давления три повороте потока на лопатках производят работу вращения ротора. В результате температура и давление торможения абсолютного потока уменьшаются так, что
1 ос ‘ ос 2
Р ос\ > Рос2-
' Характерной особенностью рассмотренного процесса является его ступенчатый характер: потенциальная энергия вначале преобразуется 1 кинетическую энергию движущегося газа, а затем на рабочем колесе кинетическая энергия преобразуется в механическую работу. Такой процесс в чистом виде имеет место в активной ступени: статические давления на входе и выходе из рабочей решетки примерно одинаковы, а скорости Wi и W2 различаются только за счет потерь в рабочей решетке.
В чисто реактивной ступени оба составляющих процесса протекают одновременно на рабочем колесе. Поток газа в рабочих каналах в относительном движении ускоряется и одновременно совершает работу вращения ротора. Широкое применение находят промежуточные типы ступеней, в которых рационально сочетаются оба принципа — активный и реактивный. В этом случае преобразование потенциальной энергии газа в кинетическую осуществляется частично в неподвижной решетке и частично в рабочих каналах.
Изменение статических параметров потока и параметров торможения в проточной части такой ступени показано на рис. 9-1,1.
Ступень может быть выполнена также с радиальным потоком газа. В такой ступени газ движется в радиальных плоскостях от оси вращения к периферии или, наоборот, к оси вращения. Радиальная ступень может бьить активного, реактивного или промежуточного типа.
Схемы проточньих частей ступеней турбины с радиальным потоком газа показаны на ри,с. 9-3. В радиальном сечении видны формы профилей направляющей и рабочей решеток ступени и треугольники скоростей на входе и выходе из рабочих каналов. Заметим, что в радиальной ступени окружная скорость меняется от входного к выходному сечению решетки.
В некоторых ступенях поток газд направлен поя углом к оси вращения. При этом радиальные составляющие скорости сг не равны нулю и при анализе свойств потока должны учитываться (рис. 9-4).
В ступени компрессора (осевого или центробежного) происходит преобразование механической работы в по-
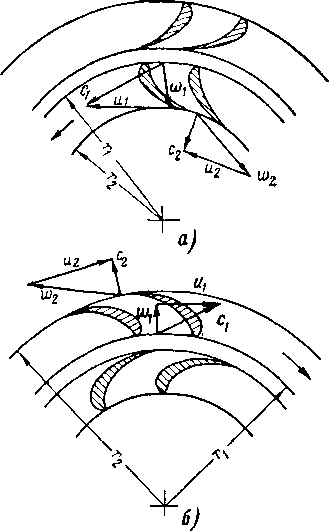
Рис. 9-3. Схемы центробежной (а) и центростремительной (б) радиальных ступеней турбины.
тенциальную энергию газа Каналы рабочей решетки 1 осевого компрессора — расширяющиеся^(рис. 9-5). Давление газа в относительном движении возрастает, а скорость уменьшается. Этот процесс продолжается в направляющем аппарате 2. Энтальпия полного торможения в абсолютном движении возрастает.
В ступени центробежного компрессора движение газа осуществляется от центра к периферии (рис 9-6), рабочие лопатки колеса 1 образуют расширяющиеся каналы, в которых происходит торможение относительного потока. Сжатие газа может продолжаться в лопаточном диффузоре 2.
В точной постановке задачи течение газа в ступени турбомашины описывается дифференциальными уравнениями пространственного потока - вязкой сжимаемой
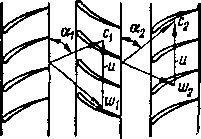
»Рис 9-5. Схема и развертка проточной части ступени осевого компрессора.
жидкости. Приближенные решения основываются на уравнениях идеальной сжимаемой жидкости, выведенных в гл. 1.
Исходные уравнения {сохранения количества энергии) целесообразно системе координат. В
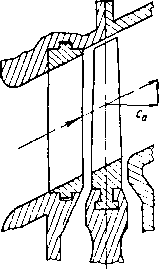
Рис 9-4 Схема диагональной ступени.
движения, неразрывности и записать в цилиндрической качестве независимых переменных, как и ранее, выбираются: радиус-вектор г полярный угол 0 и аппликата г. Направление оси х совпадает с осью вращения турбины. Тогда система уравнений сохранения в абсолютном установившемся движении
(dpjdt = dcjdt = dcjdt= dcjdt = 0)
при R = e = Z = 0 сводится к уравнениям (1-14) и (1-17а).
Для исследования потока в рабочей решетке основные уравнения идеальной жидкости целесообразно записать для
относительного движения. При этбм используются очевидные соотношения (рис. 9-2):
Wa = Ca’ Wr = Cr И Wu = Cu~U = Cu-Wr>
где ш — угловая скорость вращения рабочей решетки.

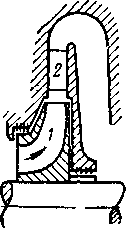
Рис 9-6 Схема ступени центробежного компрессора
После подстановки этих соотношений в уравнения (1-17а) для установившегося относительного движения получим:
dw ®udwr dw w„
Wr4F+-T~W^~Wa~dz T~ -ш*г + 2шюв = —
wu dwu
dw
w -r^-4-r дг Г
(9-1)
r
dw^ r dr
dw„
W
)
+ ~u vwa » Л1 "a
1 dp f dz '
¦ 2ww =--—
Г pr d0
w„ dw
Дифференциальное уравнение неразрывности для установившегося относительного потока имеет вид:
d (ри>г) dr
д (Р Wg) dz
1 д (раи„) г д0
Система уравнений движения (1 - 17а) и (1-14) или (9-1) и (9-2) дополняется уравнениями сохранения энергии in изоэнтропического процесса При этом система уравнений, определяющая пространственное установившееся движение идеальной сжимаемой жидкости в ступени турбомашины, является замкнутой
Перейдем теперь к выводу уравнения энергии для струйки газа в проточной части ступени Уравнение энергии может быть записано в параметрах абсолютного или относительного движения В первом случае в уравнение энергии вводятся члены, учитывающие энергетический обмен между потоком и окружающей средой Во втором случае (для относительного потока) необходимо учитывать дополнительные силы, введение которьих позволяет рассматривать относительное движение, так, как если бьи оно было абсолютным Такими дополнительными силами являются кориолисова сила инерции и центробежная сила
Уравнение энергии для абсолютного потока напишем в форме первого начала термодинамики. С учетом сделанных допущений получим:
di -{- cdc — gdL = 0.
(9-3)
Здесь LT — работа, совершаемая газом.
Величина Lr может быть определена с помощью уравнения моментов количества движения. Момент сил, действующих на рабочие лопатки при установившемся движении, будет:
![]()
где G — секундный расход газа через решетку.
Умножив Ми на угловую скорость вращения решетки ш, найдем секундную работу или мощность, которой обмениваются лопатки с газовым потоком:
![]()
Следовательно, работа, отнесенная к весу протекающего газа, равна:
(9-4)
Уравнение (9-4) получено Эйлером. В дифференциальной форме уравнение Эйлера имеет вид:
dLr — g d (cji).
(9-5)
Так как в турбине газ совершает работу, то вдоль струйки абсолютного течения d(cuu)<^ 0. Для ступени компрессора выражение внешней работы аналогично, но в этом случае d(cuu)^> 0. Использовав выражения (9-3) и (9-5), получим дифференциальное уравнение энергии для потока в абсолютном движении:
di -f- cdc — d (си) = 0.
(9-6)
В соответствии с законом сохранения энергии изменение кинетической и внутренней энергии газа в относительном движении ,равно количеству подведенного («ли отведенного) тепла и работе действительных и дополнительных сил. Так как кориолисова сила инерции натравлена нормально к оси струйки в относительном движении (к вектору w), то работа этой силы равна нулю.
Таким образом, из числа дополнительных сил в уравнение анергии для потока газа в относительном движении необходимо ввести центробежную силу, направленную вдоль радиуса нормально к оси вращения. В частном случае аксиальной ступени вектор центробежной силы нормален к линиям тока и работа центробежных сил также равна нулю.
Уравнение энергии для потока в относительном движении получаем на основании первого начала термодинамики (9-3).
Учитывая, что = ст с*а-\- с и используя связь между абсолютными и относительными скоростями, преобразуем выражение (9-6). Получим:
di wdw — udu — 0.
(9-7)
Интегрирование уравнения энергии (9-6) для потока в абсолютном движении дает:
С
(9-8)
CuU — const-
Интеграл уравнения энергии потока в относительном движении (9-7) равен:
f_j_ = const. (9-9)
Переход от уравнения (9-8) к уравнению (9-9), очевидно, совершается с помощью формулы (рис. 9-2,6)
хюг = с2-\-и2 — 2 сии. (9-Ю)
Полученные уравнения для относительного движения могут быть использованы для расчета ступени не только турбины, но и других турбомашин (компрессор, вентилятор). Направление энергетического обмена (отвод или подвод механической работы) при этом не имеег значения. Это замечание вполне справедливо только в предположении изоэнтропического течения в ступени турбо-машиньв. В реальных условиях движение газа сопровождается потерями. При этом направление энергетического обмена существенно влияет на структуру потока (на характер распределения параметров в проточной части), а следовательно, и на к. п. д. ступени.
При отсутствии потерь изменение состояния газа в абсолютном и относительном движении подчиняется изоэнтропическому закону, который для идеального газа может бьпь представлен формулой p/pK=const.
В этом случае интегралы уравнений количества движения и энергии совпадают. Действительно, для одномерного потока в абсолютном движении уравнение импульсов имеет вид: ^
cdc-j- ^ — d (саи) = 0. (9-П)
Считая относительное движение газа в ступени установившимся, запишем уравнение импульсов в такой форме:
wdw— по2 cos (r,x) dx — 0,
где гш2 cos (г х) dx — импульс центробежных сил.
Так как гш = и, то
Интегралы уравнений (9-11) и (9-12) совпадают с уравнениями (9-8) и (9-9), если di = dpjp, что соответствует изоэнтропическому процессу.
Уравнения импульсов для абсолютного и относительного движений с учетом потерь можно получить, введя в (9-11) и (9-12) импульс сил трения; в этом случае i, с и w и являются параметрами действительного течения.
При исследовании ступени в рамках упрощенной одномерной схемы потока используется уравнение неразрывности:
m = Fpc = Fpw = Fqp а = F п а а
с" UPWV*W
где Fc — площадь сечения, нормального к вектору скорости с;
Fw — площадь сечения, нормального к вектору относительной скорости w; qc и qw — приведенные расходы при абсолютном и относительном движениях.
Из уравнения неразрывности находим:
![]()
где Р<?> Р wy а с* aw — критические плотности и скорости
для абсолютного и относительного потоков.
Очевидно, статические параметры р, .р, Т как в абсолютном, так и в относительном движении одинаковы.
Действительный процесс движения газа в проточной части ступени отличается рядом особенностей, не учитываемых выведенными выше уравнениями. Так, поток газа в зазоре между направляющей и рабочей решетками обладает неравномерностью. В рабочих каналах, воспринимающих поток из зазора, течение газа оказывается периодически нестационарным, с непрерывной пульсацией скоростей и давлений.
Кроме того, поток совершает теплообмен с внешней средой в связи с непроизводительными потерями тепла и вследствие организуемого искусственного охлаждения лопаток, подверженные высоким нагрузкам. В уравнении энергии эта особенность может быть учтена введением соответствующего члена, учитывающего вмешний теплообмен.
При движении в .проточной части основной поток разветвляется; при этом некоторое количество газа, минуя рабочую решетку, протекает в зазоры между статором и ротором. В зависимости от распределения давлений в проточной части может происходить подсос газа через зазоры в основной тоток.
Таким образом, в общем случае поток газа в ступени подвергается различным внешним воздействиям, влияющим на процесс преобразования энергии. Оценка этих воздействий производится на основании данных эксперимента.
9-2. ПАРАМЕТРЫ ПОТОКА В АБСОЛЮТНОМ И ОТНОСИТЕЛЬНОМ ДВИЖЕНИИ. ОДНОМЕРНАЯ СХЕМА
ПОТОКА
Величину постоянной в правых частях уравнений энергии (9-8) и (9-9)
С2 . . W2 — и2 , . . /г> 1
~Y~ cuu.-\-t =-2--г1 = const (9-13)
можно определить из граничных условий.
При расчете ступени турбины обычно известны параметры течения на входе в рабочее колесо. Для входа имеем:
(Р1 ^
--Си\Ui + *1
= 2 + *1 =
Const.
Обозначив, как и раньше,
Т-+<9-14>
где ioc — энтальпия полного изоэнтропического торможения в произвольном сечении потока в абсолютном движении,
запишем (9-13) в такой форме:
"2~ ’ + * = *o*i с и 1М1» (9-15)
или для совершенного газа:
^де locv Тoci — энтальпия и температура изоэнтроЬичбсМб торможения на входе в рабочее колесо в абсолютном движении.
С другой стороны, при полном изоэнтропическом торможении потока в относительном движении его кинетическая энергия обратимо переходит в тепло. Энтальпия торможения определяется очевидным уравнением
W® I
-2- + ‘=‘о»- (9'16)
Следовательно, уравнение энергии принимает вид:
2
W2 — И2 . . и\ 1
2 ' — lowI ~2~ ’ (9"17)
где i — энтальпия полного торможения относительного
потока на входе в рабочее колесо.
Заметим, что если поток на входе не закручен и си]= = 0, то из (9-15) следует
Т- ~ CuU + 1 = 1ос ~ Сии = •
Такой случай может иметь место только для чисто
реактивной ступени или для ступени центробежного компрессора.
С учетом выражений (9-14) и (9-16) уравнение (9-13) можно записать так:
i —с u — i (9-18)
*ос и OW 2 4
Связь между iocV iowl, ioc и iow можно представить в виде:
Соответственно получаем зависимость между температурами торможения в абсолютном и относительном потоках:
_ Спа С„|М, ц2 и?
Г___— Т 1 — Т _— — Т__- /Р-9ГП
ос ос 1 с^ ow 2ср ow1 2ср " ' '
Уравнение (9-20) показывает, что температура торможения в обшем случае является переменной вдоль струйки величиной не только для абсолютного, но и для относительного движения. Представим (9-20) в несколько иной форме:
y^ = l-irr-' (9-20а)
1 owl р1 ow\
Tar + Ct, \U\ — C„U
= 1--?LL-4— . (9-206)
ОС I Cp* OCX
Разность температур торможения
^ r2 _ W2 (2 c„ — u) u
To~Tow=^~- =
-\Cp (9-21)
Из уравнения (9-20a) следует, что температура торможения относительного потока меняется соответственно изменению окружной скорости вдоль трубки тока. При и = const температура Тош постоянна. На этом основании можно заключить, что температура торможения Т постоянна в ступени с осевым потоком газа. В радиальной ступени Tow вдоль трубки тока меняется. Если в такой ступени поток направляется от оси вращения к периферии, то Tow увеличивается. В случае, когда поток движется к оси вращения, Т убывает.
Полученный результат имеет простое физическое объяснение.
Полная энергия относительного потока, пропорциональная Tow, изменяется вследствие работы центробежных сил, в поле которых движется газ. Если радиальные составляющие скорости не равны нулю (сг—шгФ0) и струйка газа движется не только вдоль оси вращения, но и радиально, то центробежные силы совершают работу перемещения частиц в радиальном направлении и увеличивают или уменьшают полную энергию частицы в зависимости от направления потока. Если направление относительного потока совпадает с направлением центробежных сил (радиальная ступень с потоком газа к периферии), то Tow увеличивается. В-противном случае (радиальная ступень с потоком газа к оси вращения) полная энергия уменьшается.
Формула (9-206) показывает, что температура торможения в абсолютном движении во всех случаях убывает. Из рассмотрения принципа работы турбинной ступени следует, что в произвольном сечении трубки тока сиы<си1и1 и убывает по направлению течения, так как газ совершает работу вращения колеса.
В ступени компрессора, наоборот, сии>см!ы1 и возрастает в направлении потока, так как работа к газу подводится.
Вернемся к уравнению энергии (9-13). Заметим, что величина постоянной в правой части уравнения (9-13) различна для разных струек, так как сихих может изменяться при переходе от одной струйки к другой. Отсюда заключаем, что, строго говоря, уравнение энергии следует применять для каждой струйки в отдельности. Для канала в целом уравнение (9-13) может бьпь использовано, если все величины, входящие в это уравнение, подсчитывать как средние по сечению канала.
Уравнению энергии в относительном движении можно придать известную форму, заменяя t по формуле
._ k р _ а2
тогда согласно уравнению (9-16)
w2 k р k Pow
(9-22)
(9-22а)
ИЛИ
W2 I о2 _ °L
2 “TfeZiq — feZTi ’
где pgw, po(B, aow—давление, плотность и скорость звука в изоэнтропически заторможенном относительном потоке.
Подчеркнем еще раз, что скорость звука и статические параметры течения р, р и Г для абсолютного и относительного движений имеют одну и ту же величину.
Скорость звука заторможенного относительного потока меняется вдоль струйки в соответствии с изменением энтальпии iow< При любых изменениях iow вдоль струйки сумма кинетической и потенциальной энергии относительного потока в данном сечении по уравнению (9-16) равна
i В частном случае скорость относительного потока в некотором сечении может достигнуть местной скорости звука; тогда
w = а = a,w-
Из уравнений (9-16) можно получить значение правой части уравнения энергии в виде:
2 ~ k—\ 2 k—\ '
Приравняв правые части уравнений (9-22), (9-22а) и (9-226), получим:
aOW a*W k-\-l k P°W _
low CpTOW ft—1 2 k—1 k—1 Рою
xsP1
^макс
- = i--гг ( “l — “2)‘
owl 2 * '
Аналогичные преобразования для потока в абсолютном движении приводят к соотношению
j, аос _ а*с ?+1 k Рос _
loc — Cp1oc—~kZT 2~Т^Л k— 1 ?ос ~~ =-%- = ^-(««««*-«.«“)•
С помощью этих соотношений нетрудно получить выражение для характерных скоростей а,с, смакс, a.w и т. д. Так, например, для относительного потока находим:
2fe Ро
Ж Ро
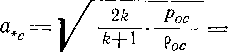
Из уравнения (9-24) следует, что характеристики абсолютного потока, зависящие от величины полной энергии ioc (от параметров торможения), меняются вдоль трубки тока. Следовательно, а,с, смакс и а являются переменными величинами для струйки газа в абсолютном движении.
В относительном движении критическая и максимальная скорости могут меняться или оставаться постоянными в зависимости от того, меняется ли или не меняется вдоль струйки окружная скорость и. Если вдоль струйки и = = const (ступень с осевым потоком), то i = const и соответственно a,w = const и дамакс = const. При переменной вдоль струйки окружной скорости эти основные характеристики потока газа изменяются соответственно изменению и.
Уравнение (9-21) позволяет установить связь между температурами торможения в относительном и абсолютном потоках в следующей форме:
(2си — и) и
Заменив
получим:
2 сии = с2 -(- и2 — w'
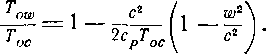
(9-25)
После замены (см., например, треугольники скоростей на рис. 9-2,6)
Тош л 2 (п си < \ 1 2 sin2 [i sin2 а „ ,
= 1 ““О
- 1 ) =
1 ““О sm2 (g — а) '
(9'25a)
и
где и0 = --.
макс
Уравнение (9-25а) показывает, что вдоль струйки отношение температур торможения меняется. При и = 0 и а=. = 2с„ отношение Т /7’„ = 1. Первый случай-соответ-
и Ot?</ ОС ^ *
ствует неподвижному колесу (м = 0), когда механическая работа газом не совершается (cuii = 0). Второе значение и определяет то сечение струйки, в котором температура торможения в абсолютном и относительном движениях одинакова.
Безразмерные скорости Мс, Mw, Хс и Xw связаны с температурой торможения в данном сечении известными соотношениями (гл. 2):
для относительного потока
If.
= 1 + *=lim2w =
kl_f 2 ;
(9-27)
1-МЛ К1
для абсолютного потока
Отсюда по известным формулам изоэнтропического процесса:
k k Pow_^ Tow^k 1 Рос _ ^ Тос 1 и Т. Д.
Pow Л Рос Л
можно получить связи между -у и Лш, —— и и т. д.
С помощью уравнений (9-27) и (9-28) можно также получить зависимость между параметрами изоэнтропического торможения в абсолютном и относительном потоках:
в виде:
k
k-i
(9-32)
С помощью уравнения (9-20) легко получить зависимость между параметрами полного торможения на входе и на выходе из колеса.
Для относительного потока получим [см. формулу (9-20а)]
i“*-l-к-=±и Л--*')
(9-33) (9-34) (9-35)
где
1
U
owl
V2i
owl
vraKcl
Соответственно для абсолютного потока [см. формулу (9-206)]
, —СИ2“2 , “| V,-,
1 oc2 I’ocX
: 1----= 1 — -Г— V (Сии), (9-36)
1ОС\ 1ОС1 """
где
Г . 11 _ Г _ 11.
(9-37)
си\ ui сы2 u2
Выразим ioel через смакс1; тогда
В формулы (9-27) — (9-39) входят безразмерные скорости абсолютного и относительного потоков. Связь между Мс и Мш выражается так:
_sin а
(9-40)
Мс sin [I '
Из уравнения
(9-41)
w2 = с2 -J- и2 — 2 сии
находим:
![]()
![]()
Последнее уравнение показывает, что отношение температур торможения T0JT0C служит переходным коэффициентом от абсолютного потока к относительному. Эта величина меняется вдоль струйки. На входе и на выходе т
из рабочего колеса для данного режима приобретает
* пп
определенные значения.
Основные газодинамические зависимости, приведенные выше, справедливы как для аксиальной, так и для радиальной ступеней турбомашины.
Практические расчеты показывают, что влияние центробежного эффекта в осевой ступени невелико116. К этому выводу легко также прийти с помощью уравнения (9-33), из которого следует, что если отношение йа/йх мало отличается от единицы, то изменение температуры торможения относительного потока пренебрежимо мало. Только при значительном изменении окружной скорости вдоль трубки тока, как это, например, имеет место в ступени центробежного компрессора или радиальной турбины, влияние указанного эффекта будет существенным.
Для обычных турбинных радиальных ступеней отношение окружных скоростей ujux колеблется в пределах
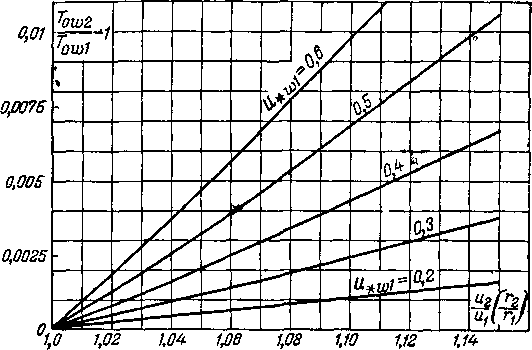
Рис. 9-7. Изменение температуры торможения относительного потока в зависимости от h2/“i иМ w\-
1,02—1,10. На основании рис. 9-7 заключаем, что для и2[и 1 = 1,10 относительное изменение температуры торможения Тощ при м,ш1 = 0,3 0,5 составляет 0,25 — 0,70%,
т. е. невелико.
Изобразим изменение состояния газа вдоль струйки в тепловой диаграмме с учетом потерь энергии в элементах ступени турбины. Параметры полного торможения на входе в направляющую решетку находим в точке О (рис. 9-8): Рос и госг Соответствующие статические параметры определены точкой 0[. Если обозначить статическое давление за направляющей решеткой рх, то точка V фиксирует состояние газа при изоэнтропическом расширении, а точка 1 показывает действительное состояние потока (с учетом потерь). Потеря энергии выражается отрезком 1 — Г.
Давление торможения абсолютного потока за направляющей решеткой будет рш (энтальпия торможения остается
неизменной). Разность р0с — Р0с1 Эквивалентна потерям энергии Дhc.
Коэффициент потерь в направляющей решетке равен:
k~\
ft
¦Ppci j _j
Ct =
H
bh fk + \ i , \
'V*-1
где Я0 — безразмерная скорость, эквивалентная изоэнтропи-ческому перепаду тепла в ступени Н0.
Разность энтальпий торможения абсолютного и относительного потоков определяется по уравнению (9-19). Откладывая величину i0cl — i0wl от точки О' на линии f0c] = const, находим точку 2, которая определяет состояние заторможенного относительного потока на входе в рабочее колесо.
В рабочих каналах в результате потерь часть кинетической энергии необратимо переходит в тепло. В результате давление торможения в относительном движении падает. Если вдоль струйки газа окружная скорость не меняется, то соответствующий процесс изображается линией 2—3 (i0 , = const). При увеличении и вдоль струйки (радиальный поток от оси вращения к периферии) iQw возрастает (пунктирная линия 2—3!). Если и уменьшается, то i0w снижается (линия 2—<3").
Статические параметры на выходе из рабочей решетки определяются в точке 4, причем отрезок 3—4' (или соот-
Aw\t
ветственно 3' — 4' и 3" — 4’) равен .
Коэффициент потерь кинетической энергии в рабочей решетке будет:
т
1 Oail
k -f- 1 ^2
1
T,
OCI Xg
Дhw A (w\t— а|)
//, — 2gJi0 ft—1 /Wl \ k
Pow2
Поток покидает ступень с некоторой абсолютной скоростью с2. Часть кинетической энергии, эквивалентная скорости с2, является потерей (Дha).
Коэффициент потерь с выходной скоростью
fe-i
Р0с2\к ^с2
ЛЛВ
С =- :
4 нл
Т()с2
‘ocl *о \Р'о'с / Х0
где рт — давление тормол ения абсолютного потока за ступенью;
/?0 — фиктивное давление торможения за ступенью (рис. 9-8).
Как видно из формул, коэффициенты потерь С2 и С3 зависят в неявной форме от — , так как от этой величи-
Сл
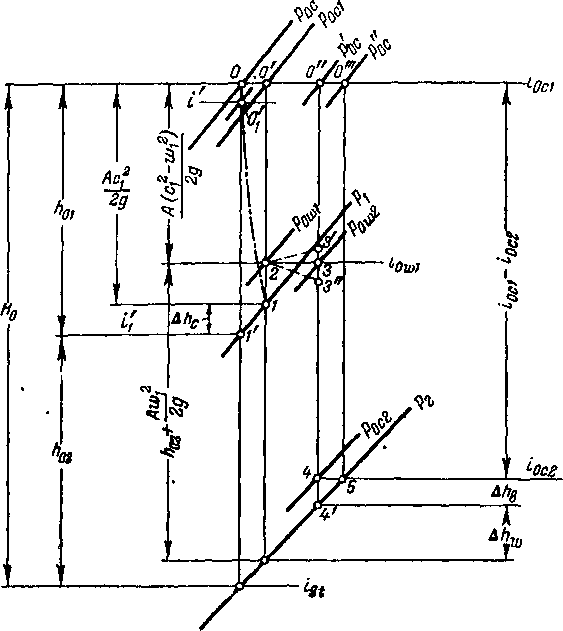
Рис. 9-8 Процесс в тепловой диаграмме для турбинной ступени 588
и Re на выходе из направляющей решетки.
^Ои>1 ^Qcl п
йы зависят отношения температур -*— и -— . Величи-
1 0?l 1 Oel
также зависит от —; при изменении р- меняются числа М
![]()
на Clt характеризующая потери в неподвил ной решетке,
В тепловой диаграмме отложим от точки 4' вверх величину Дйв; тогда получим точку 4, характеризующую состояние заторможенного абсолютного потока за ступенью-Предположим, что вся кинетическая энергия абсолютного потока за ступенью необратимо переходит в тепло; тогда на изобаре ра в точке 5 определяется состояние газа за ступенью (процесс торможения за ступенью принят изобарическим).
Введем теперь понятие степени реакции. Степенью реакции называют отношение располагаемого теплового перепада на рабочей решетке к полному располагаемому перепаду тепла в ступени. Следовательно, степень реакции указывает ту часть располагаемой потенциальной энергии газа (тепла), которая Преобразуется в механическую работу непосредственно в рабочей решетке (на колесе).
По определению (рис. 9-8)
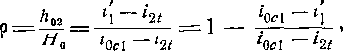
где /г02 — изоэнтропический располагаемый перепад тепла
в рабочей решетке.
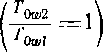
Формулу для степени реакции можно преобразовать к виду:
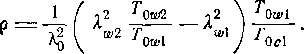
Отсюда следует, что для аксиальной ступени
степень реакции обращается в нуль при Яв2 = Яда1. Для радиальной ступени р = 0 при
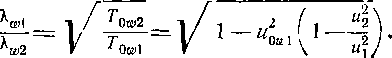
Из этой формулы следует, что степень реакции MoJKet быть равна нулю при движении газа в радиальной ступени от оси вращения к периферии («2 > при Яа] >Ящ2. При движении газа к оси вращения р = 0, если Я^ <С\,2-Действительная удельная работа, развиваемая в ступени при любой степени реакции р, может быть подсчитана по формуле
г0с2 —
k—1
¦« ^0 с2*\_ Ak пт117
1 _ к \Ръс
Отсюда с помощью уравнения (9-36) находим:
ALT — 2/^, w0(Scuk .
Тогда к. п. д. ступени на ободе можно найти по фор-
ALT
муле Tju=. Подставив сюда значения ALT и Нй, по-
** О
лучим:
Из формулы видно, что даже в случае, когда потери энергии в направляющей и рабочей решетках отсутствуют (С1 = С2 = 0), к. п. д. ступени на ободе равен нулю при 'Lcji - 0.
Формула (9-37) показывает, что такое условие выполняется, если
Си1М1 = Си2иг-
Очевидно, что в этом случае поток газа в ступени работы не совершает. Величина Ъсии — 0 и для неподвижного колеса (и1~и2 = 0). Максимальное значение iju соответствует (Zcuii )чакс = cuiut.
Легко видеть, что в рассматриваемом случае си2иг = 0, или си2 = 0 (и2 ф 0).
По треугольникам скоростей можно заключить, что при этом выходные потери минимальны, так как при си2 — 0
9-3. УРАВНЕНИЯ ДЛЯ РАСЧЕТА РАСПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ПОТОКА ПО РАДИУСУ В РАМКАХ СТРУЙНОЙ ТЕОРИИ •
Рассмотрим поток газа через ступень осевой турбомашины (рис. 9-9). Выберем три контрольных сечения: О—0 — перед направляющей решеткой, 1—1 — между направляющей и рабочей решетками и 2—2— за рабочей решеткой.
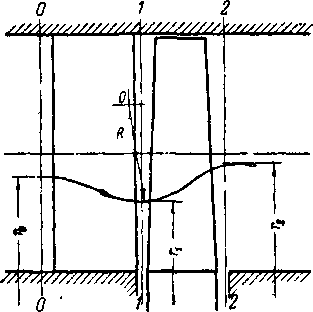
Рис. 9-9 Схема проточной части ступени с длинными лопатками.
Найдем распределение параметров таэтока по радиусу в двух контрольных сечениях (1—¦
1 и 2—2), если известны: распределение
параметров в сечении О—0, давление газа на корневом или среднем радиусе сечения 2—2, геометрические размеры ступени, число оборотов ротора турбины и аэродинамические характеристики решеток.
Имея в виду трудности, связанные с исследованием пространственного течения сжимаемой жидкости, можно в первом приближении рассмотреть упрощенную осесимметричную схему ,потока в ступени турбомашины.
Так, если принять, что течение в гступени является установившемся и осесимметричным (д/дд='0), а радиальные составляющие скорости (cr = w ), а также их произ-'дс, дс, dw, dw.
~дг ’ ~дг ’ ~дг J весьма малы> то уравнения (1-17а) и (9-1) упрощаются и принимают вид (R=Q=z-~ 0):
водные
дг
1 dp си . dcu n.
(9-43)
dca
'adz
<toa “ dz
1 dp p dz
W
¦Первое уравнение (9-43) выражает условие радиального равновесия частицы газа, при котором центробежные силы на любой из соосных цилиндрических поверхностей уравновешиваются силами статического давления газа. Так, согласно обозначениям на рис. 9-9 для единицы длины зазора (сечение 1—1) можно записать: 2nrdp\ = 2nrdr p\C2ui/r и получить из него первое уравнение (9-43).
Второе уравнение (9-43) выражает условие неизменяемости си по оси ступени. Из третьего уравнения нетрудно получить dca/dz = 0 три dp/dz=0, т. е. если давление по оси не меняется, то осевые составляющие скорости также сохраняются неизменными.
Принятым допущениям в наибольшей степени отвечает поток в контрольных сечениях 1—1 и 2—2\ движение в межлопаточных каналах не подчиняется таким упрощенным закономерностям.
Введем дополнительно ряд упрощений. Пренебрегаем периодической нестационарностью потока, вызванной вращением рабочего колеса, или, точнее, считаем, что рассмотрение осредненных по времени скоростей также не вносит существенной ошибки. Предполагаем также, что после перестройки поток в контрольных сечениях движется по цилиндрическим поверхностям (т. е. радиусы кривизны меридионального сечения поверхности тока R на рис. 9-9 достаточно велики). Считаем, что внешний и внутренний теплообмен отсутствует, а решетки ступени обтекаются безотрывно.
Рассмотрим поток за направляющей решеткой. Воспользуемся упрощенным уравнением радиального равновесия (9-43), записав его в следующей форме: для сечения 0—0
Cg cos2 а0
1 dp0_
где р0, р0, pt, pj, с0, я0, си аг — давления, плотности, скорости и углы потока перед и за направляющей решеткой.
Предполагаем, что функция ai = ai(r) известна. Вид этой функции определяется принятым законом закрутки направляющих лопаток. Очевидно, что поток газа должен удовлетворять уравнениям энергии и неразрывности. Для каждой элементарной кольцевой струйки, протекающей через направляющую решетку, уравнение энергии можно записать в такой форме:
/о' = 't + 4 =^ f‘ ¦ (9-45)
где i’Q — энтальпия торможения в зазоре;
clt, clt iu, ii —скорости и энтальпии газа в конце изоэнтропического и действительного процессов расширения в направляющей решетке;
-ц1 — к. п. д. направляющей решетки (приближенно определяемый как ij^cp2).
Продифференцируем уравнение (9-45) по радиусу г:
dig dlu , i /2-гhc^ci—cfdi], \ ^
Q_
dr dr ”Г~ 2 \ „2
T), dr
diu
Производная характеризует изменение энтальпии
потока в зазоре за направляющей решеткой по радиусу и, как известно, может быть записана таким образом:
1 dPi Pi ' dpi (9-47)
dr pu dr pu Pl dr • ' "
Здесь pu — плотность газа в конце изоэнтропического расширения в направляющей решетке; — плотность газа в конце действительного расширения (при наличии потерь).
1
Х,= А= —=(-Т-Ц—1 • (9-48)
Ро 118
где ^lt = Cu/u сХ—теоретическая безразмерная скорость за направляющей решеткой.
Следовательно, производная
dHt 1 dpt !r ~ycJ^~dF ’
или с учетом (9-436) di
11
• (9-49)
dr
Подставляя (9-49) в уравнение энергии (9-46), получаем дифференциальное уравнение распределения абсолютных скоростей по радиусу в зазоре:
где hol = (? /2ij1 — располагаемый теплоперепад в направляющей решетке в данном сечении по радиусу.
Интегрируя уравнение (9-50), находим:
с1 = К1 ехр
где KL — постоянная, отвечающая исходному (среднему или корневому) сечению.
Уравнение (9-51) в рамках рассматриваемой струйной задачи является наиболее общим.
Из (9-48) следует, Ч'го при дозвуковых скоростях и умеренных потерях в направляющей решетке отношение плотностей Рг1?и близко к единице. Расчеты позволяю!-установить ту область значений Яи и %, в которой можно принять = 1. Без большой погрешности такое упрощение допускается прй Яи<[1.
При сверхзвуковых скоростях функция ус должна быть сохранена в уравнении (9-50). Однако в некоторых случаях можно использовать упрощенные зависимости хс{^и, ти), а при слабом изменении Хи и по радиусу ic принимается для каждого участка постоянной. Имея в виду, что 1С зависит от %и и следует заключить, что при точном расчете ступени на сверхзвуковых скоростях метод последовательных приближений становится неизбежным.
Следует подчеркнуть также, что влияние сжимаемости косвенно учитывается в уравнении (9-51) функциями и ijj. В зависимости от числа Мх меняются потери и угол выхода из направляющей решетки. Следовательно, вид функций -у)! (г) и а1(г) зависит от Mt; согласно (9-51) при изменении этих функций меняется и характер распределения абсолютных скоростей (г) в зазоре.
Необходимо также отметить, что уравнения (9-50) и (9-51) справедливы для любого закона закрутки.
Перейдем теперь к расчету потока за рабочей решеткой. При сделанных выше допущениях условие радиального равновесия в сечении 2 — 2 выражается первым уравнением (9-44):
сечение 2— 2 будет малым (и1 и2). Тогда уравнение
энергии для относительного потока можно представить в известной форме:
, ¦ , w2 h + — = + ~2tfe ’ (9-53)
где о»! — относительная скорость на входе в рабочую решетку;
— энтальпия газа перед рабочей решеткой;
Tjg — к. п. д. рабочей решетки (т^^ф2); ht — энтальпия газа за рабочей решеткой в изоэн-тропическом процессе.
Теоретическая и действительная скорости за решеткой связаны соотношением
= V Ч* w2t ¦
Очевидно, что i2t = i2t (г) и ш2 = ш2 (г) являются искомыми функциями, а тг13 = т)2 (г) и wl = w1 (г) могут рассматриваться как заданные функции радиуса г.
Энтальпия потока за направляющей решеткой определяется по уравнению энергии:
i0=i 1
После подстановки i1 в (9-53) находим:
г’о = гм +
2i)2 2
Продифференцировав уравнение энергии, получим (полагаем <#' /dr = 0):
i dffi)2 С?1)г I d /" C?
I w2 uw2 * u'l2 I ц I 1 1 \__ Г1 /Q СЛД
dr I“ i)j dr ' 2tj2 dr "I dr \ 2 J (9-54)
Заменим в уравнении (9-54)
dhL = A _L ^3 = V (®г cos h - И)г
dr р2 р2; dr Л® r
![]()
Уравнения (9-54), (9-55) и (9-56) решаем совместно. После некоторых упрощений получаем искомое дифференциальное уравнение:
![]()
![]()
— 2x^2“ cos %w2 + ц, = 0. * (9-57)
Уравнение (9-57) является нелинейным. Оно линеаризуется только в частном случае, когда d(calr)jdr = 0.
Интегрируя (9-57) в этом случае, т. е. с учетом d (c,i г)
—j— = 0, находим:
Г
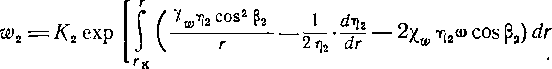
(9-58)
где Кг — постоянная, определяемая для исходного (среднего или корневого) сечения.
Условие d(cuir)/dr = 0 выполняется строго при закрутке ступени по методу постоянной циркуляции *. Однако, как показывает опыт, это условие приближенно осуществляется и в ряде других практически важных случаев.
Постоянные К\ и К2 в уравнениях (9-51) и (9-58) определены, если известны скорости С] и w2 в каком-либо сечении по высоте лопаток. Эта задача решается применением ур-авнения неразрывности для сечений 1-1
и 2-2:
G = 2*ga,cl?tci ] ?isin aidr> (9'59)
ГК
r
G = 2^а,т2^т2 j q 2sin p ,dr. (9-60)
<K
Входящая в уравнение (9-58) функция %w при упрощенных решениях может быть принята равной %w = const для всей ступени или отдельных кольцевых струек К
Следует также отметить, что дифференциальное уравнение (9-57) для неподвижного рабочего колеса (со = 0) переходит в уравнение (9-50).
9-4 РАСЧЕТ ПОТОКА В СТУПЕНИ С ДЛИННЫМИ ЛОПАТКАМИ ПОСТОЯННОГО ПРОФИЛЯ
Рассмотрим ступень с осевым потоком газа, полагая, что поток на входе в направляющую решетку имеет равномерное лоле скоростей. Поставим следующую задачу: установить распределение параметров в зазоре и за рабочей решеткой по радиусу, если лопатки имеют постоянный профиль по высоте. Решение этой задачи позволяет дополнительно получить исходные данные для расчета ступени с лопатками постоянного профиля по аэродинамическим характеристикам решеток и может быть использовано для определения той предельной веерности решеток, при которой можно применять лопатки постоянного профиля.
Расчет ступеней с лопатками .постоянного профиля можно выполнить, полагая постоянными углы по радиусу си и Рг. Более точный прием расчета, излагаемый ниже, состоит в том, что углы cti и Рг задаются в виде функций радиуса г. Этот способ целесообразно применять в тех случаях, когда веерность ступени оказывается значительной.
Многочисленные опыты показывают, что угол можно выразить в зависимости от относительного шага или радиуса формулой
tg<*i= tg Я1к + (0 — 1) (7 — 1), (9-61)
1 Поток газа в ступени за направляющей и рабочей решетками является закрученным, т. е. имеет неравномерное поле скоростей как при абсолютном, так и в относительном движении. Как показано в § 5-16, в таком потоке поле полной энергии будет неравномерным.
A tgcr, =tg«lB-tgaiK;
а1в> а1к — углы выхода потока у вершины и соответственно в корне воч сечении, r = rjrk; rk — радиус корневого сечения, г — радиус текущего сечения;
I I
Подставив (9-61) в уравнение (9-50) и проинтегрировав последнее, получим:
- с, F(r)
(9-62)
L\k
Здесь
-(r-l)*
F(r)-
1 + га.
2n,b, — b, (0
1 -f- га,
(9-63)
1 + [га,-6,(0-I)]2 ’
1
=-2_ (tg«|B —tga1&)
Для определения скорости необходимо знать величину в корневом сечении. С этой целью преобразуем уравнение неразрывности (9-59), записав 'его для сечений 0 — 0 и 1 — 1:
q0 о
T-Ve-119)’
(9-64)
Picalri drii
са\ = Cj sin а, =
с 1 tga,
V1 + tg2a,
или приближенно
F(r)
cal =clAclsinai = /'tft^^ sin al> C9-65)
где dj принимается до формуле (9-61,.
Приведенные выше зависимости справедливы, если^поток в зазоре дозвуковой. При смешанных течениях в зазоре, когда в нижней
части ступени (у корневых сечений) Ci>e,i, формула (9-62) неприменима. В этом случае необходимо учитывать отклонение потока в косом срезе направляющей решетки.
Перейдем теперь к расчету потока за ступенью. Воспользуемся основным уравнением (9 57) и проинтегрируем его при т)2= const и d (сп1и) = 0 для принятого закона изменения углов по радиусу
Здесь b»2fe — значение ш2 в корневом сечении;
Р2й — угол вектора w2k\
q ={1 — [пг — 62(0 — I)]2}; пг= sin?2fe;
1 1
Ьг A sin {52= -j- (sin р2в — sin p2fe).
При известных значениях ш2 легко определяется располагаемый теплоперепад в ступени.
С помощью выведенных уравнений можно рассчитать распределение параметров по радиусу в зазоре н за ступенью с лопатками постоянного профиля.
Располагаемый теплоперепад в направляющей решетке согласно (9 62) будет:
7- _ ^01 ~2 (r)]2 ,Q R7.
~ Л01к ~ 1 ~ ~г2к ' ( ^
Найдем изменение степени реакции по радиусу:
Л 01 , Л01к— , , Л01к Нок
р-‘-Н0 А« Н0к Н0 ’
*01к
Н 0к= Рк’
где рк — степень реакции в корневом сечении.
Использовав (9-67), получим:
Отсюда можно получить приближенную формулу для определения реакции на среднем диаметре ступени с незакрученными лопатками, исходя из заданной величины рк в исходном — корневом — сечении. Замечая, что гт = 0/0 — 1 и полагая Ь1 5= 0, из формулы (9-68) получаем:
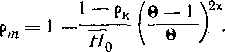
(9-69)
Формула (9-69) имеет ограниченную область применения Очевидно, что она справедлива для относительно больших 0, так как только в этом случае разность а, у вершины и у корня мала и можно принять b,^0.
Минимальную степень реакции в среднем сечении можно определить, полагая, что в корневом сечении 0. Тогда из (9-69)
получим:
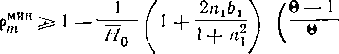
или приближенно 5=0)
![]()
Изменение работы на венце по радиусу можно найти по формуле:
![]()
- си\ са2
¦‘¦'r/к cu2k
где са2 = w2k wt cos р2 — и.
Функция ся1 (г) также известна. Следовательно, величина Lu (г) определена.
Поле осевых составляющих скоростей за ступенью рассчитывается по формулам:
Са2 = Сй2 tg “2 = ^„2 tg h = (°U2 + «) tg h
В заключение отметим, что исходная формула для степени реакции (9-68) позволяет определить разность р у вершины и у корня лопатки. Так как
- 0 + 1 гв — 0 — 1 ’
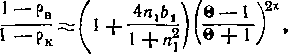
то после подстановки в (9-68) получим:
где рв — степень реакции у вершины.
Для прикидочных расчётов^можйо^рёйомендойать формулу 1 — рв (в—1 \2
1 — Pk^Vw+I/ <9'70)
Используя полученные соотношения, можно проанализировать изменения параметров ,по радиусу в зазоре и за ступенью и оценить дополнительные потери, возникающие в ступени с лопатками постоянного профиля.
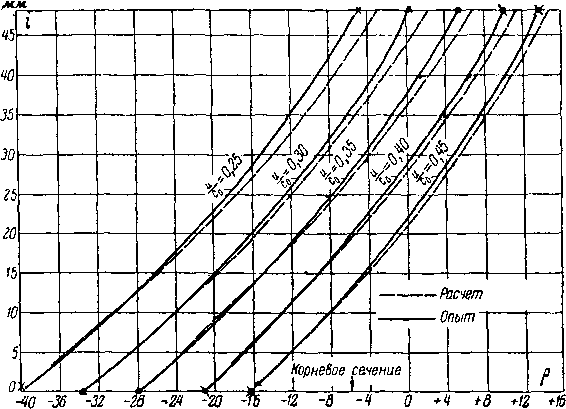
Рис 9-10. Сравнение опытных и расчетных значенлй степени реакции в различных сечениях по радиусу ступени с лопатками постоянного профиля; в = 7,73; М0 = 0,65.
Результаты соответствующих расчетов показывают, что дополнительные потери в ступени с незакрученными лопатками обусловливаются увеличением выходных потерь, изменением угла входа потока на рабочую ’решетку, а также изменением отдаваемой работы по радиусу. За ступенью поток вихревой; выравнивание поля скоростей сопровождается потерями кинетической энергии, которые должны быть включены в общий баланс потерь ступени.
Результаты расчетов по предлагаемой методике удовлетворительно совпадают с экспериментальными данными.
Подробное экспериментальное исследование потока в зазоре и за ступенью с цилиндрическими лопатками было выполнено в МЭИ при Q = d/l = 7,73. Был произведен расчет испытанных ступеней по приближенному методу, изложенному выше. Соответствующие кривые изменения реакции по радиусу приведены на рис. 9-10. Сравнение показывает удовлетворительную сходимость опытных и расчетных значений реакции. Опытные и расчетные значения углов, давлений и скоростей также удовлетворительно совпадают.
В заключение отметим, что при больших в изменение углов ai и Рг по радиусу невелико.
Расчет скоростей Ci и w2 в таких ступенях можно производить по формулам, которые легко получить из основных уравнений (9-50) и (9-57) при следующих допущениях: г) 1 = const; т)2” const; ai = const и Рг = const.
9-5. НЕКОТОРЫЕ СПОСОБЫ ПРОФИЛИРОВАНИЯ ДЛИННЫХ ЛОПАТОК СТУПЕНЕЙ С ОСЕВЫМ ПОТОКОМ ГАЗА
Изложенная выше методика расчета ступеней с лопатками постоянного профиля позволяет оценить дополнительные потери в ступени, обусловленные изменением параметров и углов потока по радиусу в зазоре, а также возрастанием выходных потерь.
Результаты такого расчета приведены на рис. 9-11. Здесь даны кривые, устанавливающие дополнительные потери в ступени с лопатками постоянного профиля в зависимости от Q=d/l. Кроме того, на график нанесены опытные значения дополнительных потерь Ат]м. При е<ю дополнительные потери превосходят 1%. Следовательно, в таких ступенях необходимо специальным образом организовать поток, обеспечивая минимальные потери энергии. С этой целью лопатки направляющей и рабочей решеток выполняют закрученными (винтовыми) с переменным профилем по высоте.
Закрутка лопаток может быть осуществлена различными методами. Исходное дифференциальное уравнение распределения скоростей в зазоре (9-50) имеет бесчисленное множество решений. В соответствии с этим число методов закругки лопаток теоретически может быть бесконечно большим. Однако только незначительная часть этих методов отвечает условиям рациональной организации потока в ступени турбины. По этой причине, а также имея в виду, что уравнение (9-60) является приближенным, следует развивать те методы профилирования, которые строятся на четких физических предпосылках.
В практике турбостроения наибольшее распространение получили следующие методы организации потока в зазоре: а) постоянной циркуляции скорости при рав-%
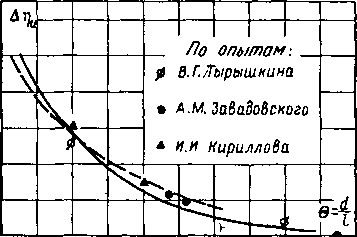
3 V 5 В ? 8 9 10 11 12" 13
Рис. 9-11. Уменьшение к. п. д. ступени от незакрутки лопаток в зависимости от e = d/i; сравнение расчетных и опытных значений Дт)я.
10 В 6 ч
2
0
номерном поле осевых скоростей [си\Г=const); б) постоянного по радиусу направления абсолютного потока (си = const); в) специального выбранного закона изменения направления абсолютного потока [ai=/(r)], включая направляющие лопатки постоянного профиля.
Организация потока за рабочими лопатками осуществляется в предположении: а) равномерного поля абсолютных скоростей; б) постоянства работы, развиваемой потоком в различных сечениях по радиусу; в) постоянства располагаемого теплолерепада по радиусу.
Количество сочетаний любых перечисленных способов организации потока в зазоре и за ступенью ограничивается условием неразрывности, связывающим поток в этих сечениях.
Рассмотрим в качестве примера изоэнтропиче-ское течение газа в ступени при равномерном поле осевых скоростей в зазоре и за ступенью (метод постоянной циркуляции скорости).
В этом случае коэффициенты т) = х=1, dt0 = 0 и уравнение (9-50) приобретает простой вид:
— -j-cos2^-^ = 0. (9-50а)
С1 г
Так как
с1йс1 = сяХйсяХ-\-са1йсл
и согласно принятому допущению саХ = const, то уравнение (9-50а) преобразуется к виду:
Интегрируя это уравнение, получаем: calr = const.
Последнее условие выражает постоянство циркуляции скорости вокруг направляющей решетки. Действительно, в простейшем случае осевого входа в направляющую решетку (с 0 = 0) циркуляция скорости равна:
Г =1 (с,п ~ с»о) = tc,n —^Гси\ — const-
где z — число лопаток в решетке.
Основоположником рассматриваемого метода является Н. Е Жуковский. Еще в 1912 г. при исследовании воздушных винтов Н. Е. Жуковский показал, что осевые скорости постоянны в радиальном направлении, если изменение окружных составляющих скоростей соответствует закону постоянства циркуляции. Хорошо известно, что воздушные бинты, а затем и вентиляторы, построенные согласно вихревой теории Н. Е. Жуковского, отличались высокой экономичностью. Для расчета длинных лопаток паровых и газовых тур'бин этот метод был впервые применен В. В. Уваровым.
С помощью уравнения (9-50а) нетрудно пайти распределение абсолютных скоростей в зазоре:
— ci — at
ci = —l Cal = -— = const.
cik ш c\k
Изменение реакции по радиусу устанавливается с помощью очевидных соотношений
.2 „2
с, с'
1 L\k
Р=1-
ИЛИ
1--=r^ [1 + (/¦“ — 1) sin» а1Л ]. (9-71)
В соответствии с условием cat г = const можно найти изменение углов абсолютной скорости по радиусу в таком виде:
гсп
tg «1 = - 120
'а\ У1
а\
Закрутку лопаток по условию постоянства циркуляции скорости можно осуществить с учетом потерь в решетках.
Для адиабатического течения (с учетом потерь) расчетные зависимости, полученные путем интегрирования исходных дифференциальных уравнений, даны в табл. 9-1.
Для течения с потерями, как это видно из формул, приведенных в табл. 9-1, условия cur = const и cai=eonst являются несовместимыми. При условии равномерного поля осевых скоростей в зазоре циркуляции скорости вокруг направляющей лопатки должны увеличиваться к ее вершине. Если в основу профилирования ступени положено условие постоянства циркуляции скорости, то осевые скорости в зазоре также несколько .увеличиваются к вершине.
Адиабатическое течение в зазоре при aj = const и rji = const подчиняется уравнению, получаемому инте-грированием (9-50), в следующем виде:
--Тс,--T),cOS2 a,
С! = — — Г
;с1к
сп\
cal =cal/culK cos 01,
I
sin a|K
VI — tj, eos2ajK (I — r2); r ' 1 — coss а1к [r,, + (l — тц) r)
“Ik
r }/ 1 — TjiCOs2alK (1 — r2)
1 — Tj! cos2 <x]K (1 — r)
_XJ[__
j/” 1 — r^cos^iK (1 — r3)
r 1 — cos2 aj K lr]2 + (1 —TjO r2]
tgPi
/
^/2cosai_K_
«Ок
2
w2k
tt 2k —
"Й—(1_r '> я0к
Следовательно, располагаемый теплоперепад в направляющей решетке будет:
— “о--2llicos2 ai
Л01 = С, = Г
Отношение скоростей меняется по радиусу в соответствии с формулой
и — l+’li cos2 a,
~^==ХкГ
где x = u.Jc|K — отношение скоростей для корневого сечения.
Угол относительного потока
sin aj
COS a,—Хк г
Следует подчеркнуть, что осуществление метода закрутки при ai = const приводит к направляющим лопаткам переменного профиля по высоте, так как при малых 0 значительно меняются шаг лопаток и скорость с j вдоль радиуса. Следовательно, чтоб ы> осу щес т в ит ь условие ai=const, необходимо менять установочный угол профиля ау, т. е. выполнять лопатку закрученной. При больших скоростях необходимо также учитывать влияние сжимаемости на средний угол за решеткой, что также приводит к необходимости закручивать направляющие лопатки.
Для большого числа ступеней представляется возможным направляющие лопатки выполнять без закрутки. Расчет направляющих решегок производится по формулам, приведенным в § 9-4. С помощью этих соотношений рассчитываются параметры потока в зазоре.
Расчет рабочих лопаток как при ai = const, так и при «1 —f(r) производится, исходя из принятых условий за ступенью. Как указывалось, могут быть приняты условия отсутствия закрутки потока на выходе (си2 = 0), постоянства работы по радиусу (Lu = const) и др.
Расчет ступени при течении, близком к цилиндрическому, можно осуществить, разбив поток на ряд элементарных кольцевых струек. В пределах каждой струйки можно считать задачу одномерной и применять обычную методику расчета. Закрутка направляющей решетки, вообще говоря, может быть выбрана любой: ai = const; си\Г=const; a\=f(r). При этом, естественно, для определения параметров в зазоре можно воспользоваться одним из частных решений (9-50). Определив параметры в зазоре, записываем уравнения неразрывности для каждой струйки в контрольных сечениях 1—1 и 2—2:
ДО , .
Pu
AG ,
р2( ЯРгЩ! 12i
где AG — расход пара через элементарную струйку;
и Ргt — плотности в конце изоэнтропического расширения в направляющей и рабочей решетках;
cu, w2t — теоретические скорости выхода потока; ft и /2 — площади выходных сечений в пределах одной элементарной струйки; jj-i, ja2 — коэффициенты расхода в данном кольцевом сечении направляющей и рабочей решеток.
Из уравнения неразрывности и треугольников скоростей определяем параметры, необходимые для проектирования рабочей решетки. Полный расход газа через ступень О равен сумме расходов по всем элементарным струйкам. Общий к. п. д. ступени находится по к. п. д. элементарных струек как усредненный по расходу.
При подобном методе расчета коэффициенты расхода щ и fig и коэффициенты скорости <р и <]> следует принимать переменными, зависящими от геометрических и режимных параметров в рассматриваемых сечениях решеток. Описанный метод расчета весьма прост и дает надежные результаты.
Построение направляющей и рабочей лопаток осуществляется по данным расчета закрутки. По вычисленным значениям Ме1 (г) и а, (г) подбираются профили в корневых, средних и верхних сечениях направляющей решетки. При больших теплоперепадах в ступени в корневых сечениях >1, а в периферийных М^, <[ 1 • Соответственно корневые сечения образуют профили группы В (с обратной вогнутостью в косом срезе и небольшим расширением канала), средние сечения — профили группы Б (прямолинейные участки спинки в косом срезе), а верхние — профили группы А (выпуклая спинка в косом срезе). Аналогично строится рабочая лопатка, для которой исходными служат параметры: (г), Mw] (г), Mw2 (г) и р2 (г). При построении
желательно выбирать шаги и установочные углы профилей в диапазоне оптимальных значений.
Рассмотренные выше способы профилирования дают практически совпадающий характер изменения реакции по радиусу, что непосредственно вытекает из приближенного уравнения (9-50).
Некоторые различия обнаруживаются в распределении углов абсолютного и относительного потоков ai и (5ь а также осевых составляющих скорости.
Сравнение трех Методов закрутки (си\г — const, а\ — const и для цилиндрического течения ргcei = const) приведено на рис. 9-12. Несколько большую закрутку рабочей решетки дает метод ai = const. При этом направляющие лопатки оказываются наименее закрученными. Для метода профилирования cuir = const закрутка рабочих лопаток уменьшается, а направляющих — возрастает. Промежуточные результаты получены для цилиндрического течения, отвечающего закономерностям потока, организованного по методу си\Г= const при рь=const.
Опыты показывают, что ступени, спрофилированные указанными методами, имеют практически одинаковую эффективность. Дальнейшее повышение к. п. д. ступеней можно, по-видимому, обеспечить путем выбора рационального распределения реакции по радиусу. Такому условию отвечает закон р(Р), при котором радиальные градиенты давления в корневых сечениях будут минимальными.
9-6. ОСЕВАЯ СТУПЕНЬ С МАЛЫМ ИЗМЕНЕНИЕМ РЕАКЦИИ ПО РАДИУСУ
Возможность осуществления ступени турбомашины с уменьшенным изменением реакции по радиусу представляет большой практический интерес. В турбинной ступени выравнивание реакции приводит к более равномерному полю скоростей в зазоре, к уменьшению разно-
Zfi
%8
| Г |
се.=const | ||||||||
| cons |
t | ||||||||
| к |
75-v | / | / | / | |||||
| ( |
Joty'ts | 25/ | ) | ||||||
| / | / |
1 f | / |
'о,С | / | ||||
| ( f / | / t | / |
|||||||
| / |
/ | А | / | / | °ul |
•r- | con |
ft | |
| // |
у | / | / | ||||||
| 1 | h |
'/ | / | ||||||
| if | V, // | ||||||||
| Ч/ | У |
1iff | Ctf | ||||||
| f | |||||||||
Ш
1,0 tг /,*
2J0
I
1,в
| r | |||||||||
| °ш-г | =con | $ |
j | ||||||
| Р,°аГт | |||||||||
| а,=г |
wnst | ||||||||
| 7/ | |||||||||
| /-¦ |
J | ||||||||
| У/ | |||||||||
| V | |||||||||
| А/ | |||||||||
|
r | |||||||||
гп
3JB
о.г о.« o,s о,8 р Рис. 9-12. Сопоставление некоторых методов закрутки лопаток.
сти углов входа потока Pi в верхнем и корневом сечениях, к снижению лотерь от утечек, уменьшению осе-зых усилий и т. п. Для компрессорной ступени с реакцией р=0,5 за счет выравнивания поля скоростей по высоте может быть отодвинута предельная граница по числу М, повышены окружные скорости и, следовательно, увеличен коэффициент напора при сохранении высокой экономичности ступени.
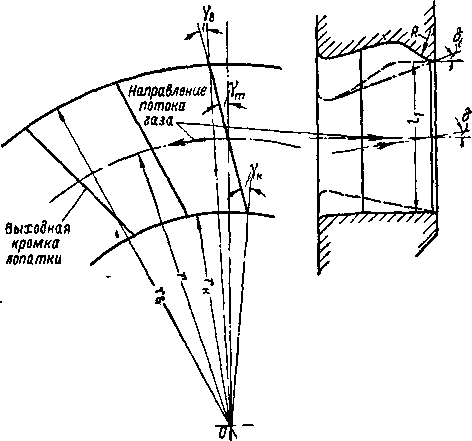
Рис. 9-13 Схема кольцевой решетки направляющих профилей с наклонными кромками и меридиональным профилированием.
Для ступеней турбин с небольшими высотами лопаток (Т < 0,8 и @5* 13) выравнивание реакции может быть осуществлено применением меридионального профилирования каналов направляющей решетки по высоте.
Условие равенства центробежных сил, действующих внутри канала на элемент массы от окружной и осевой составляющих скорости, т. е. условие постоянства статического давления по высоте канала, можно представить в таком виде:
Р<с?,
R
(9-72)
Здесь R — радиус кривизны верхнего обвода в меридиональной плоскости; гк — радиус корневого сечения (рис. 9-13).
Из (9-72) находим:
Как указывалось (§ 8-8), применение меридионального профилирования в ступенях с небольшими высо-
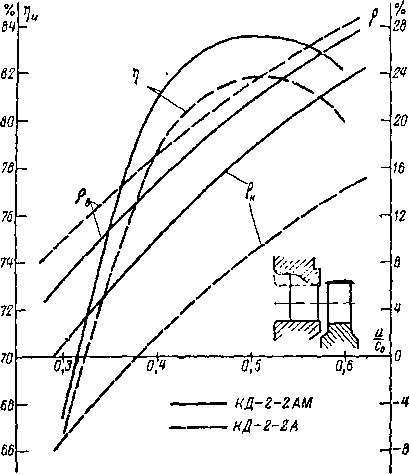
Рис. 9-14. Зависимость к. п. д. к)ог и реакции от и/с0 для ступени с меридиональным профилированием (КД-2-2Ам) и ступени с цилиндрическими обводами (КД-2-2А); 8 = 16; = 0,5.
тами лопаток позволяет не только уменьшить разность [реакций, ,но и значительно уменьшить потери ® 'Направляющих решетках. На рис. 9-14 представлены резуль-гаты испытаний двух ступеней (ii»0,5; 0=16) с криволинейным и цилиндрическим обводами верхнего бандажа. Видно, что ступень с мериодинальным профилированием имеет более высокий к. П. д. (на 1,5—2%), а разность реакций Др — рв — рк уменьшается более чем в 3 раза (с 16 до 5%).
Для ступеней с 0<1О меридиональным профилированием трудно добиться значительного выравнивания
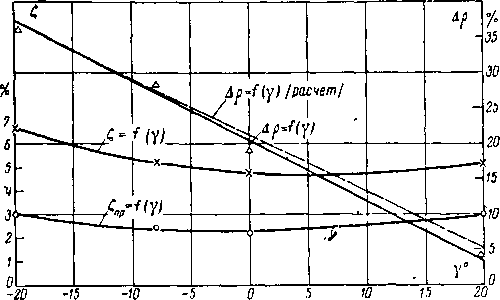
Рис. 9-15. Изменение разности реакции Др~профильных и суммарных потерь в решетках в функции угла наклона лопаток у (® = 8,5; =
= 1,0; а, = 15 ).
реакции без существенного увеличения потерь в направляющей решетке.
Для предельных значений 2,5<©<5 с целью снижения градиента статического давления ,по радиусу целесообразно применять наклон лопаток в радиальной плоскости. Действительно, из уравнения радиального равновесия, записанного с учетом сил воздействия лопаток на поток,
дсг
дг
др ' дг
(9-73)
г L F
дс> 'а дх
(где Fr—радиальная составляющая силы воздействия лопаток на поток) видно, что при 7v<0 (наклон лопаток по потоку, рис. 9-12) градиент давления меньше, чем при радиальной установке лопаток. Физически это
означает, что на элемент газа действует сила, направление которой противоположно направлению центробежной силы. Следовательно, в этом случае уменьшается разность статических давлений, обеспечивающих равновесие элемента газа ’.
Таким образом, наклоном направляющих лопаток в плоскости вращения можно изменить распределение статического давления в зазоре и распределение реакции по радиусу.
На рис. 9-15 представлены результаты испытаний четырех кольцевых решеток с различными углами наклона у = 20; 0; —8; —20°, проведенных в МЭИ. Как видно из графика, с увеличением угла наклона лопаток по потоку разность реакций в периферийном и корневом сечениях значительно уменьшается; для 0«8, Др~0 может быть достигнуто при у~25°. На этом же графике нанесены профильные и суммарные потери в решетках.
В пределах изменений угла наклона у от —8 до +8°' профильные потери практически не меняются и составляют 2—2,5%. При у~+20° и у ——20° профильные потери возрастают до 3%. Этот результат объясняется искажением формы межлопаточных каналов при большом наклоне лопаток.
Суммарные потери в решетках остаются практически постоянными в пределах изменения угла у от —8 до +20°. Интенсивный рост потерь наблюдается при углах наклона —8°>у>+20°. Графики изменения потерь по высоте решеток (рис. 9-16) показывают, что для отрицательных углов наклона потери возрастают в корневых сечениях, где возникает отрыв потока. Для решеток с наклоном лопаток по потоку, когда осуществляется поджатие потока в корневых сечениях, .потери увеличиваются в периферийных сечениях.
Опыты показали, что одновременным введением меридионального профилирования верхнего обвода решетки и наклоном лопаток можно уменьшить потери в верхних сечениях (у>0). При этом оба фактора — наклон лопаток по потоку и профилирование верхнего
1 Исследование ступеней с наклонными лопатками проведены Ю. И. Митюшкиным (ЛМЗ) и Г. А. Филипповым (МЭИ).
обвода — позволяют более резко снйзить разность реакций Др — рв рк.
Приближенная формула для определения реакции в ступени с различными углами наклона лопаток у может быть получена путем совместного решения уравне-
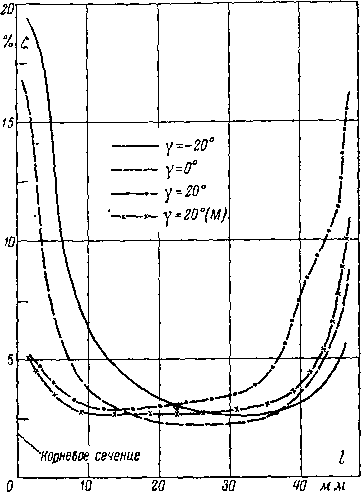
Рис. 9-16. Характер изменения потерь по высоте решетки при различных углах наклона лопаток (в = 8,5; /, = 1,0; а, = 15°).
ний количества движения и радиального равновесия цилиндрического потока (9-73). Сила воздействия лопаток на поток определяется через окружную составляющую по уравнению (сг«0):
р _ Рч .. °a dC"
Г tg (90—y) tg (90—у) dx ’
где Рп — окружная составляющая силы воздействия лопаток на поток.
ГТринйв линейный з&кон изменения tu ho Ширийё решетки для средней линии канала са = хся1/В, получим:
Cj COS Ct j
F=cl sin а. -п—,кп-\ •
r 1 1 В tg (90 — y )
Подставляя Fr в уравнение (9-73), находим:
2 •> 2 i
dp Cj cos c?j C| sin a, cos a,
dr
dr.
zJtg(90 —y)
Из последнего уравнения совместно с уравнением энергии получим:
cfc,
sin a. cos a, , „dr
—: —r~/Is-т dr — cos2 a. — .
ct о tg (90 — y) r
Проинтегрировав это уравнение для случая at = const получим распределение скоростей по высоте лопаток:
i Г sin dj cos a, (r,— rR) eX^ I о tg (90 — y)
J \cos2 ax
(9-74)
Реакция в произвольном сечении зазора рассчитывается по формуле
2sin a, cos (r, — r )
I \ 2 cos2 ax
Ч|к
Р=1-(1-Рк)
exp
й tg (90 — y)
(9-75)
Разность реакций при pA = 0 и 6^1,5В (b — хорда профиля)
( 3tgi,'
У
Др=1
(9-76)
ехр
2 tg (90 — y)
Полученные формулы дают несколько завышенные значения разности реакций, что связано в основном с отклонением потока в зазоре ступени от коаксиального, наличием радиальных перетеканий газа в пограничном слое лопаток, утечками в ступени, влиянием рабочего колеса. Погрешность расчета объясняется также принятым приближенным законом изменения си по оси канала и пр.
Влияние перечисленных факторов учитывается по -опытным данным введением коэффициента Л = 0,65 в формулу (9-76).
Расчет реакции в ступени с наклоном лопаток по потоку и меридиональным профилированием зерхнего обвода осуществляется по формуле
![]()
![]()
(9-77)
полученной с учетом влияния кривизны верхнего обвода на распределение скоростей по радиусу в зазоре.
Опыт подтверждает' удовлетворительную точность формулы (9-77) при 0 > 6.
Для ступеней с малыми в<5 и сзерхкритическими теплоперепадами применение наклона лопаток также целесообразно. Действительно, при большой веерности проточной части (рис. 9-17) поджатие потока лопатками позволяет улучшить обтекание корневых сечений; обтекание верхних сечений практически не изменится, так как угол наклона ув у периферии значительно меньше, чем у корня. (Так, например, для ступени с 0 = 2,6 и ут = 9° наклон у вершины yb = 5°40', а у корня ук= 14°.) Уменьшение реакции в верхних сечениях и соответственно уменьшение угла входа потока на рабочие лопатки (3j приведет к уменьшению закрутки рабочей лопатки.
Перераспределение теплоперепада между' направляющей и рабочей решетками и уменьшение угла пери
ферийных сечениях, обусловленное наклоном лопаток по потоку, облегчают профилирование верхних сечений рабочей решетки при сверхзвуковых скоростях.
Влияние наклона направляющих лопаток з ступени 0 = 2,6 и s2 = 0,27 на распределение параметров по радиусу показано на рис. 9-17. При наклоне в среднем сечении Ym==-j-3° реакция в верхнем сечении снизилась с 75 до 56е/„, угол входа потока уменьшился со 155° до 127°. Число Мс1 возросло у вершины лопатки до 0,9, а число М^г уменьшилось до Мда2=1>08.
Последние ступени турбин часто приходится выполнять с коническими обводами (рис. 9-12). Наличие конусности приводит к уменьшению реакции в ступени.
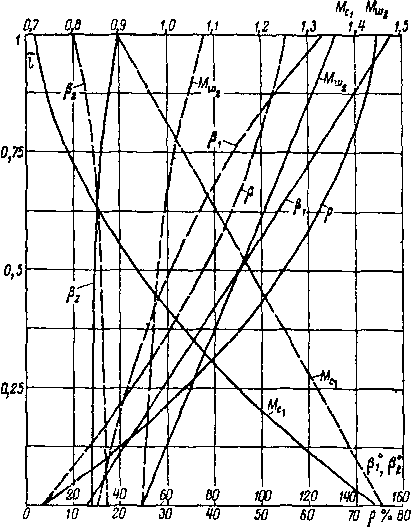
Рис. 9-17. Изменение параметров по высоте лопатки (0 = 2,6; е2 = 0,27).
-----с наклоном кромок, -—кромки радиальные.
Для конусной направляющей решетки изменение реакции по радиусу можно приближенно определить по формуле
/ 1 \ 2 cos’ ct, ¦«
где /C,=l-{-siii2a,tg28B — коэффициент, учитывающий влияние конусности; 8в — угол конусности у вершины.
МЕТОДЫ
ЭКСПЕРИМЕНТАЛЬНОГО ИССЛЕДОВАНИЯ ГАЗОВЫХ ПОТОКОВ И ПРОТОЧНОЙ ЧАСТИ ТУРБОМАШИН
10-1. ЭКСПЕРИМЕНТАЛЬНЫЕ СТЕНДЫ ДЛЯ ИССЛЕДОВАНИЯ ПРОТОЧНЫХ ЧАСТЕЙ ТУРБОМАЩИН
Задачи опытного исследования проточной части турбомашин можно разбить на тр'и группы В первую грулпу включаются вопросы, связанные с исследованием структуры потока в отдельных, рассматриваемых изолированно элементах ступени и в первую очередь в направляющей и рабочей решетках
Вторая группа задач заключается в дифференцированном изучении физических явлений, происходящих в ступени
Третья группа задач сводится к определению опытных коэффициентов, необходимых для теплового расчета турбомашины, и к выяснению зависимости этих коэффициентов от основных конструктивных, геометрических и режимных параметров ступени
Основные требования к эксперименту в лабораторных условиях формулируются теорией подобия Практически не все эти требования могут быть реализованы с одинаковой степенью точности, так как действительные процессы в турбомашине отличаются большой сложностью Поэтому при постановке эксперимента в каждом отдельном случае следует установить наиболге существенные особенности процесса, пренебрегая его второстепенными признаками Правильное решение этого вопроса определяет направление и методику экопримента, а также теоретическую и практическую ценность результатов исследования Если основной целью эиспер лмента является получение интегральных характеристик ступени, то очевидно, что в модельных условиях должны быть воспроизведены все наиболее существенные признаки процесса Поэтому опытное исследование характеристик ступени необходимо проводить на специальных экспериментальной турбине или экспериментальном компрессоре, позволяющих установить надежные значения характеристик и изучить основные особенности потока в решетках
Последняя задача, однако, решается в экспериментальной ча^-шине нелегко, так как требует применения сложной специальней измерительной аппаратуры. Поэтому при детальном изучении обтекания решеток, при изучении механизма образовании и развития потерь в изолированно рассматриваемых решетках необходимо прибегать и к другим, более простым методам эксперимента, поступаясь некоторыми требованиями теории подобия Отсюда следует, что наряду с использованием экспериментальной турбомашичы в качестве основного метода исследования необходимо применять и более простые и поэтому широко распространенные методы испытания неподвижных решеток
Исследования элементов проточной части паровых и газовых турбин могут производиться на водяном паре или на воздухе, при-
Чем схема йсйктателыШй Менда сущ&стйемно За1й?йт От Приме няемого рабочего тела Исследования элементов ком пресс о,р а производятся, естественно, на воздухе
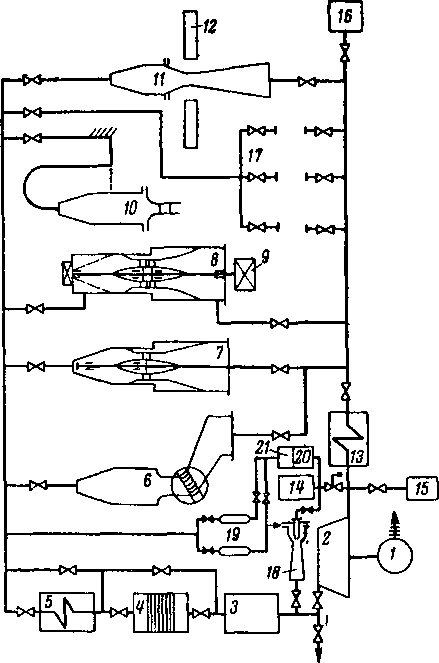
Рис 10-1 Принципиальная схема воздушного экспериментального стенда 1 — двигатель; 2—компрессор, 3— ресивер, 4—фильтр; 5 — подогреватель; 6 и 7 —статические установки, 8, ^—экспериментальная турбина 10 — установка для взвешивания реактивных усилий, 11 — аэродинамическая труба, 12 — оптическая установка, 13—холодильник, /<#—дополнительный компрессор;
15—фильтр, /6—глушитель, 17—стенд испытания клапанов, эжекторов и т п , 18—эжекюр, 19—баллоны, 20 и 21—фильтр и влагоотделнтель
Принципиальная схема воздушного экспериментатьного стенда для исследования проточных частей турбин и компрессоров представлена на рис 10 1
Воздух сжимается компрессором 2 и, проходя через ресивер 3, очищается в филь-пре 4 В случае необходимости температура воз ’ духа может быть поднята в воздухоподогревателе 5 Это особенно важно при достижении в исследуемой решетке больших скоростей, когда температура воздуха резко падает, что вызывает конденсацию водяных паров, всегда находящихся в воздухе
Очищенным и подогретым воздухом питаются эксперименталь-мые установки для исследования плоских неподвижных решеток 6 и для исследования кольцевых неподвижных решеток 7, воздушная экспериментальная турбина 8, установка, работающая на принципе взвешивания реактивных усилий 10, аэродинамическая труба 11 с оптическими приборами 12 и блок 17 для испытаний эжекторов, патрубков, клапанов и т п
Кольцевая аэродинамическая труба 7 спроектирована так, что, помимо пневмометричесиих измерений, позволяет измерять крутящий момент и осевое усилие на исследуемой решетке Аналогично спроектирована и воздушная экспериментальная турбина 8 с гидравлическим или индукционным тормозом 9
Аэродинамическая труба является необходимым элементом стенда и предназначается дня тарировочных испытаний различных измерительных приборов и необходимых методических работ На плоской установке 6 или аэродинамической трубе И проводятся эксперименты с применением оптической аппаратуры 12 Стенд может работать как по открытой, так и по замкнутой схеме Замкнутая схема, являясь более сложной, дает, однако, возможность независимого изменения чисел М и Re, т е позволяет раздельно исследовать влияния сжимаемости и вязкости Для постановки ряда экспериментов это требование является оановным
При использовании открытой схемы воздух выбрасывается в атмосферу через глушитель 16 При работе по замкнутой схеме воздух через охладитель 13 подается во всасывающую линию компрессора
-Для создания в замкнутом контуре стенда повышенного давления и возмещения утечек через неплотности и уплотнения необходим дополнительный компрессор 14 с давлением, превышающим максимальное давление во всасывающем патрубке основного компрессора Если компрессор 14 имеет достаточные степень сжатия и производительность, то для ряда режимов вместо основного ком прессора 2 могут быть использованы компрессор 14 и эжектор 18, питающие экспериментальные установки воздухом пониженного давления
В случае необходимости проведения эксперимента, требующего больших секундных расходов и высоких акоростей, может быть применена баллонная схема, состоящая из компрессора 14 и пруппы баллонов 19 В течение определенного времени баллоны 19 наполняются компрессором 14 через фильтр 20 и влагоотделитель 21 Затем воздух из баллонов через регулирующие вентили направляется в экспериментальную установку Так как при работе давление в баллонах будет падать, то для поддержания постоянного режлма экспериментальной установки необходимо использование автоматически управляемых вентилей Кратковременность действия— основной недостаток баллонной схемы
Методика эксперимента на воздухе при температурах порядка 50—>100° С значительно проще, че>м «а паре при температурах 250—350° С Это определило широкое применение воздуха в лабораторных исследованиях проточных частей цурбомашин
Однако ряд задач, связанных с длительной работой эксперимента тыкых установок с большими секундными расходами и при больших скоростях, требует чрезвычайно мощных и громоздких компрессорных установок Работы, связанные с исследованием последних ступеней конденсационных паровых турбин, могут проводиться на воздухе только частично, а ряд вопросов вообще не может быть решен на воздушном стенде
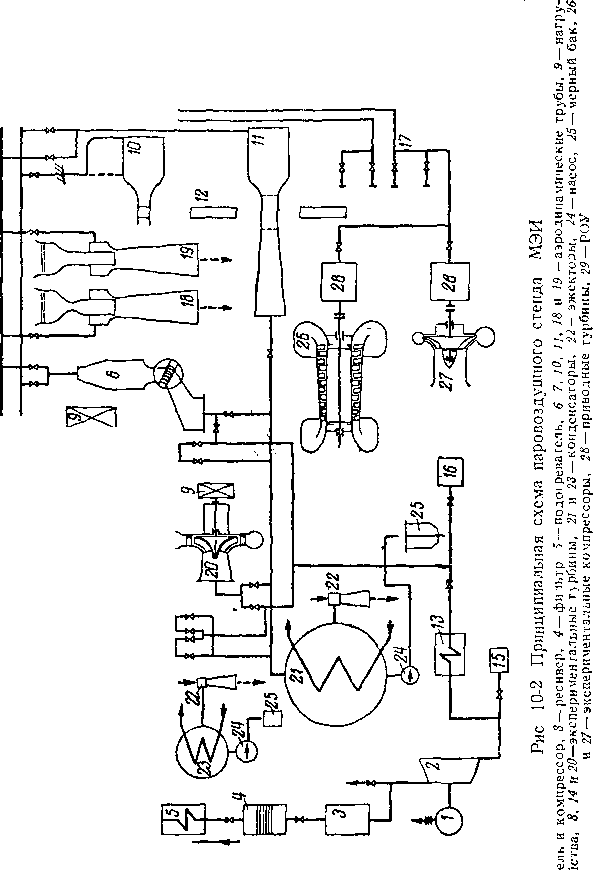
Оптимальным решением, дающим наибольшею возможность ведения различных исследований проточных частей турбин с минимальной затратой времени и средств, является использование ком бинированного паровоздушного стенда, принципиальная схема которого приведена на рис 10-2
Большинство установок такого стенда может работать как на паре, так и на воздухе, что позвочяет выбирать оптимальный для данного эксперимента вид рабочего тела Воздушный контур стемда-не отличается от приведенного на рис 10-1 Использование пара позволяет легко получать большие секундные расходы, большие скорости, независимо менять числа М и Re, обеапечивает проведение всех исследований, связанных с влажностью Пар через редукционно-охладительную установку 29 подается к экспериментальным установкам стенда, проходит через них и направляется в основной конденсатор 21 Конденсат конденсатным насосом 24 подается в мерный бак 25, а затем в линию возврата конденсата ТЭЦ
Паровоздушный стенд состоит из установки для исследования кольцевых неподвижных решеток 7, высокооборотной одноступенчатой экспериментальной осевой турбины 8, двухвальной экспериментальной турбины 14, предназначенной в основном для исследования последних ступеней, экспериментальной турбины для исследования радиально осевых ступеней 20, осевого 26 и центробежного 27 экспериментальных компрессоров с паротурбинным приводом 28 и установки для испытания плоских решеток 6
При необходимости в паровоздушном стенде могут быть использованы эжекторные аэродинамические трубы 18 и 19, воздушный поток в которых создается паровым эжектором, засасывающим воздух из атмосферы
В схему стенда включен блок 17, позволяющий устанавливать для периодических испытаний различные вспомогательные детали турбин
Для отсоса пара из уплотнений экспериментальных турбин используется вспомогательный конденсатор 23 Вакуум в конденсаторах поддерживается паровыми эжекторами 22
Выхлопные патрубки турбин жепательчо снабжать дроссельными устройствами, позволяющими поднимать противодавление за рабочим колесом до 3—5 ата Для подавляющего большинства экспериментов достаточно давление свежего пара 5—7 ата при температуре 250—350° С
Редукционно-охладительная установка должна допускать питание стендов не только перегретым паром пониженных параметров, но и влажным паром
т щ
| >1 п |
Lr- (Г |
|
«-1 | |
| 0,-^2 <ОТ Jil п_ | j п |
10-2. МЕТОДЫ ИЗМЕРЕНИЯ ПАРАМЕТРОВ РАБОЧЕГО ТЕЛА ПРИ ИССЛЕДОВАНИИ ГАЗОВЫХ ПОТОКОВ
Основными параметрами рабочего тела, непосредственно измеряемыми в процессе эксперимента, являются давление и температура полного торможения, статическое давление, а также направление и величина вектора скорости При исследовании нестационарных явлений измеряются частота, амплитуда и форма изменения тех же параметров во времени
Для измерения давлений в газовых потоках применяются различные насадки
Размеры исследуемых решеток обычно невелики, особенно при испытаниях на больших скоростях Следовательно, размеры насадка должиы быть минимальными, чтобы не происходило ощутимого искажения исследуемого поля Значительная неравномерность потока за решеткой также заставляет предельно уменьшать размеры приемника и менять его конструкцию в отличие от широко известных насадков, применяемых для измерения в относительно равно мерных потоках
Рассмотрим некоторые конструкции насадков Давление полного торможения измеряется насадками, схематически изображенными на рис 10 3 Совершенство насадка характеризуется безразмерными коэффициентами
Ро Роь _ Рйч
р°= ~ Г ’ v*>= '
2 Рс
где Кр0~~коэффициент, характеризующий чувствительность насадка к изменению угла атаки, ч—коэффициент, характеризующий качество приемника, ро — действительное давление полного торможения Ъри угле атаки 6 = 0, рт измеряемое давление торможения при данном 5^0, рои— измеряемое давление торможения при 6=0
Экспериментально установлено, что при 6=0 коэффициент примерно одинаков для всех приведенных на рис 10 3 форм носика иасадка и близок к единице Величина Кр существенно зависит от формы носика, что иллюстрируется характеристиками на рис 10 3
Для измерения давления торможения вблизи стенок, где имеются значительные градиенты ро, применяются микронасадки Для измерений в ограниченных областях, например в зазорах между направляющими и рабочим аппаратами, применяются насадки типов д и е. Насадок д более пригоден при малых скоростях и отличается от насадка е только меньшей жесткостью
Для измерения статического давления применяются насадки, схемы и характеристики которых приведены на рис 10 4 Измерение статического давления представляет трудности из за необходимости более строгой ориентировки оси насадка по направлению вектора скорости потока
Чувствительность насадка к изменению угла атаки потока и ка-
чесгво приемника статического давления характеризуются следую щими безразмерными коэффициентами
Р-Рч
к,
Ро~ Р'
Рь Р '' 1 Трс2
где — давление, показываемое прибором при данном угле атаки; р — статическое давление невозмущениого потока, ри—измеряе
мое давление при 8 = 0
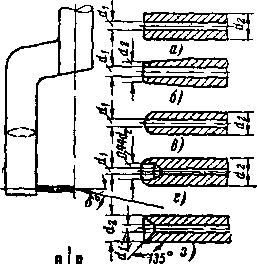
dj/dfOJS 0.2
¦?г
J-
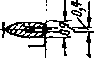
е)
^77
¦0,9
77777Я!77777777777'/ Г ж) -41-1
S* ' и
У-ЦР
*)
и
4,1
0,3
| Кр, | ihjjf | 'Ill j iz | |
| - |
ё г)' |
li/ | 1 Wj |
| - | /7 |
ту | // / r |
| C^.L. ... | , |
V,V
уо
0,05
| ** i |
h | ЧЩ | —d |
| // |
t-pi- | rf | |
| — d Г1 | |||
| « | 2 | C_i_r_ 0 30 ’¦ | )‘J |
Рис 10 3 Насадки для измерения давления торможения а—з — формы приемников и результаты тарировки.
Для измерения статического давления в потоках дозвуковой скорости удовлетворительные результаты дает насадок типа б Насадок состоит из трубки со сферическим носиком, диаметром d = = 0,9—1,2 мм с двумя приемными отверстиями диаметром di — = 0,2 — 0,3 мм. Измерения в зазорах и других труднодоступных
Рис. 10-4. Насадки для измерения статического давления
а—е—формы приемников и результаты тарировки.
Местах иногда требуют применения насадков типов в, г и д, отличающихся большей жесткостью, меньшими линейными размерами, но и худшими характеристиками.
Для измерений статического давления при сверхзвуковых скоростях применяется насадок а, имеющий благоприятную характеристику. Независимо от конструкции насадка приемные отверстия его удобно располагать на оси вращения.
При обтекании насадка полного торможения сверхзвуковым потоком перед носиком образуется криволинейный скачок Предполагая, что нейтральная линия тока пересекает элемент прямого скачка,
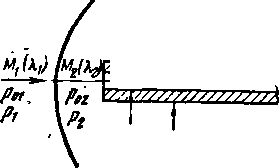
Рис. 10-5. Криволинейный скачок перед носиком насадка полного давления.
можно использовать уже известные уравнения для определения давления полного торможения, если известны безразмерная скорость набегающего потока Mt и статическое давление рг (рис. 10-5).
В условиях эксперимента обьнно удается измерить рг и давление торможения за скачком р0г- С помощью уравнений прямого скачка нетрудно найти связь между Р„г!Рг иpJfi и окончательно
Pi _ Рг Pi
получить зависимость для —--- —— , позволяющую определить
Р 02 Р 02 Pi
М, (или Aj):
— 1
Рог \ k + 1 X2. ) ,2
f [4AM? — 2 (A — 1)]*—Г1 =2 | &+1 2ft | •
I (6 + l)ft-1Mf“1 J
Вместо непосредственных расчетов по этой формуле удобно пользоваться таблицами функций прямого скачка или диаграммой скачков.
Для измерения направления вектора скорости в газовом потоке применяются разнообразные конструкции угломерных насадков: сферические, цилиндрические, трубчатые и клиновые. Наиболее удобными являются трубчатый и клиновой угломерные насадки (рис. 10-6). Сферические и цилиндрические насадки не могут быть рекомендованы .из-за сложности изготовлений, Мрйрав4сй й значительных погрешностей при измерениях в неравномерном потоке.
С помощью трубчатого или клииового .насадка направление скорости определяется ото .разности давлений, измеряемых на поверхности клина на одинаковом расстоянии от кромки.
В потоках больших дозвуковых и сверхзвуковых скоростей насадки типов а и б имеют примерно одинаковую характеристику.
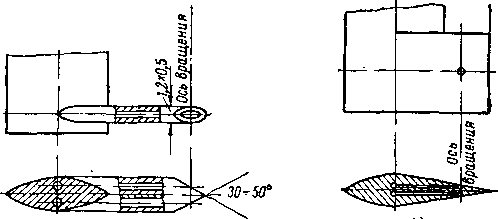
6)
У
мм рт ст
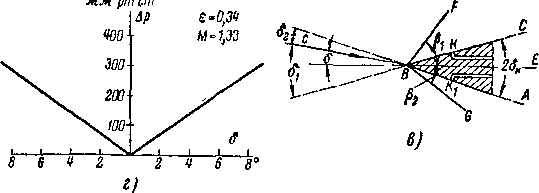
Рис. 10-6. Насадки для измерения направления вектора скорости в точке; г — результат тарировки.
Насадок типа а имеет большие линейные размеры, менее вибро-устойчив, но более точен и в меньшей степени нарушает поток вблизи точки измерения. Насадок типа б более жесткий и компактный, но не допускает измерений вблизи ограничивающих поток стеиок.
Если клин ABC (рис. 10-6,в) расположен под углом атаки б к линии тока, то головная волна, возникающая в точке В, при jWi> 1 будет несимметрична относительно оси клииа BE. Следовательно, давление в точке К будет более высоким, чем в точке К\. При б>б» вместо окачка BG может возникнуть всиша разрежения. Разность давлений Рк—рк\ при этом еще больше увеличивается. Так как первоначальная ориентировка оси насадка известна, то, поворачивая насадок до наступления равенства давлений рк и рК) по лимбу, устанавливают направление скорости потока. Желательно, чтобы угол заострения насадка был меньше предельного угла, при котором образуется криволинейный скачок, существенно снижающий чувствительность насадка.
Измерение еШйчебКои Фёмпёрктуры ДбйЖУтцёгойй газ! йызывйет значительные трудности. Сравнительно просто может быть измерена температура торможения, методы измерения ее рассматриваются ниже.
Существует большое количество конструкций термонасадков для измерения температуры торможения, основанных на одном и том же принципе: струя исследуемого газа тем Или иным способом затормаживается, и термочувствительный элемент помещается в зону заторможенного потока.
Температура торможёния Та связана со скоростью йотока и статической температурой Т известным соотношением:
![]()
Термоприемник, введенный в область заторможенного потока, из-за теплообмена с внешней средой и неполного торможения будет иметь некоторую температуру Ти ограниченную пределами
![]()
фицйент восстановления термоприемника. Измерив температуру Тt и зная из тарирово шых испытаний величину Г, нетрудно подсчитать истинную температуру торможения Т0 по формуле
![]()
Основные требования, предъявляемые к термонасадку, сводятся к следующему; 1) величина г должна быть возможно 'ближе к единице, так как при r= 1 Ti — T0; 2) величина г должна оставаться неизменной в возможно более широком диапазоне чисел М и Re;
3) габаритные размеры термонасадков должны быть минимальными.
Как правило, чувствительным элементом термонасадка служит термопара. В последнее время получают распространение полупроводниковые термоэлементы (термисторы), обладающие более высокой чувствительностью.
На рис. 10-7 и 10-8 приведены некоторые схемы и характеристики термоиасадков, наиболее подходящих к условиям экспериментального исследования проточных частей гурбомашин. Для исследования температурных полей за ступенью можно рекомендовать термона-садки типа г, обладающие весьма стабильными характеристиками. Такие насадки нечувствительны к углу скоса потока р пределах ±(10-н12)°. Для измерений в зазорах ступеней турбомашши наиболее подходящим является термонасадок типа б.
Несюолыко улучщениая модификация пояеречмо обтекаемого малоинерциоиного насадка, допускающего измерения при повышенных давлениях с полной герметизацией, приведена на рис. 10-7,в. Один электрод этого .насадка выполнен в виде помсоотенвой, иадри-мер медной, трубки размером 1,1X0,8 мм, внутри которой в фарфоровой соломке вставлен второй электрод.
.После установки внутреннего электрода торец трубки зашлифовывается и покрывается тонким слоем электролитической меди. «Спай» такой термопары при диаметре внутреннего электрода по-
€t8
0,7
V,6
| Г | и а) у | ||
|
А -2,4 | |||
| ' 4 _| |
|||
| • |
» | . м |
0,9 О,В
|
Г | и 6) | ||
| 1 | , м |
0,2 0,3 0.« 0.5 0,6 0,7 0,8 0,9 1,0
Q2 0,3 OJi 0,5 0,6 0.7 0,8 0,9 1,0
| Hs |
Z | 3 | |
| 6 | 8 |
10 | |
| A |
9 | 13 |
17 |
| d |
8 | 12 |
16 |
| d, |
3 | 4,5 |
6 |
| 0,7 | 4), 7 | 1,2 |
|
№ | 1 |
2 | 3 |
|
В | 6 |
10 | /5 |
|
Ъ | V |
8 | 12 |
|
d | 5 | ||
| 0,75 |
1,5 | 2^5 | |
| гг | 3f,7 |
47,3 | |
| 1, |
15,7 | 25 |
37,5 |
| h |
8 | 10j |
15,7 |
| d„ |
0,7 | 12 |
? |
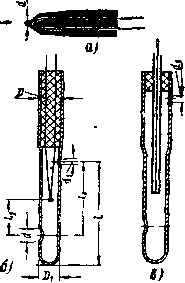
к г)

| * г | -Л | .... *1 1 | |||
| 1L | —--50 | 13 | ¦”Т *** | |
Рис. 10-7. Термонасадки для измерения температуры торможения и результаты их
тарировки.
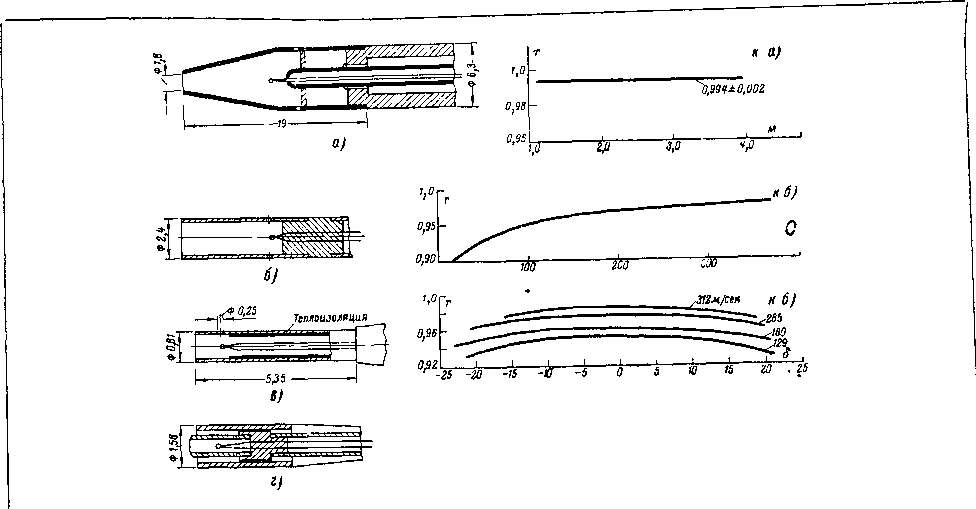
Рис. 10-8. Продольно обтекаемые термонасадки и результаты их тарировки.
рядка 0,05- мм обладает ничтожной инерцией, а сам термоприемник весьма лепко уплотняется. На рис. 10-8 приведены конструкции и характеристики насадков, применяющихся при больших сверхзвуковых скоростях и значительных температурах Хорошие результаты показал насадок типа а.
Корпус экра,на и чувствительного элемента этого насадка выполнен из иварца, покрытого слоем платины, что значительно уменьшает когавективный и лучистый теплообмен при высоких значениях То.
Для измерения температуры торможения в пограничном слое и ® потоках с малым живым сечением может с успехом применяться термонасадок в, однако изготовление насадка столь малых размеров представляет определенные трудности
При исследованиях в области повышенных температур, где приходится считаться с лучистым теплообменом, может быть использован термонасадок г, нечувствительный к скосу потока в пределах ±12° и экранированный двойным экраном
При сравнительно больших размерах исследуемого поля удобно применять комбинированные насадки, дающие одновременно значения двух и более параметров Некоторые конструкции таких насадков приведены на рис 10-9 Насадок а применяется для одновременного измерения давления полного торможения и направления плоского дозвукового потока
Насадок б широко применяется в МЭИ при одновременном измерении давления полного торможения и направления плоского дозвукового и сверхзвукового потоков и является наиболее совершенным из насадков подобного типа.
Гребенчатый иасадок удобен при измерении давлений полного торможения в потоках с малым изменением углов по сечению.
Дисковый насадок может применяться для одновременного измерения статического давления и направления плоского потока. Насадки а и б на рис 10-10 применяются для одновременного измерения давления полного торможения .и статического давления Насадок в, состоящий из трубок полного торможения и трубки Вентури, нечувствителен к углам сксса потока вплоть до 40—45°, что делает его весьма удобным в ряде экспериментов, где поворот иасадка для ориентации егй оси затруднителен.
На рис 10-10,г представлен комби тированный насадок для измерения давления и температуры полного торможения, предложенный И. Цубером.
Процессы, протекающие в ступенях турбомашин, являются периодически нестационарными Поэтому значительный интерес представляют методы измерений параметров неустановившихся газовых потоков
Так как при исследовании нестационарных процессов приходится иметь дело с частотами, достигающими тысяч герц, непосредственное измерение параметров обычными приборами становятся невозможным.
1 Ниже рассмотрены только некоторые из числа разработанных способов измерений в неустановившихся потоках. Электрические схемы измерительных устройств, описанные в прилагаемой специальной литературе, выходят за рамки книги и не рассматриваются-
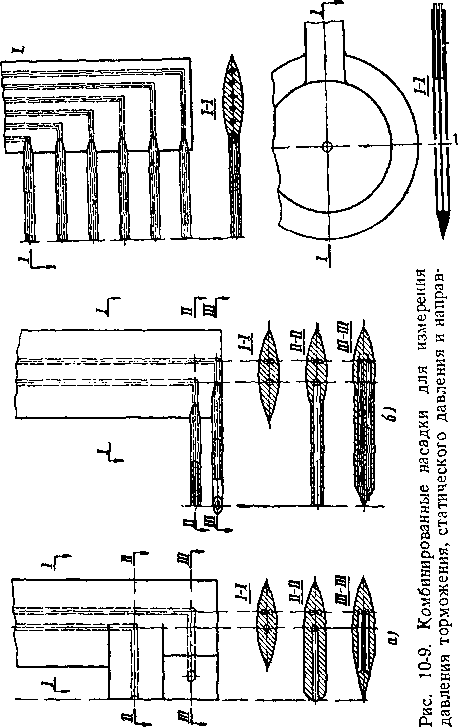
ления вектора скорости.
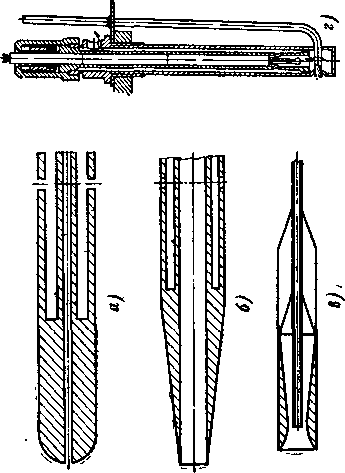
Рис. 10-10. Комбинированные насадки для измерения давления торможения и статического
давления.
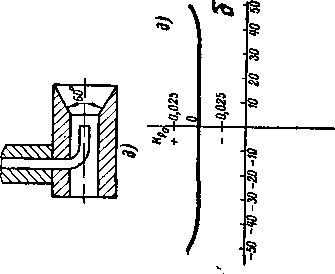
В этом случае пользуются специальными малоинерционными насадками, однозначно преобразующими измеряемый параметр в ток или э. д. с некоторой величины По изменению во времени тока или
э. д. с судят об изменении измеряемого параметра.
В основу проектирования малоинерционного насадка с электрическим преобразователем могут быть положены разные физические принципы (изменение сопротивления, емкости и т. п. в функции, например, давления|)
Желательно, чтобы выбранный принцип обеспечивал измерение возможно большего числа параметров нестационарного потока
Для возможно более точной регистрации формы исследуемого процесса собственная частота преобразователя должна по меньшей маре на порядок превосходить максимальную частоту изменения исследуемого параметра. Усилительная аппаратура, обычно применяемая совместно с датчиками, должна иметь линейную частотную характеристику.
Осуществление усилительной и регистрирующей частей измерительной установки с подобными требованиями не представляет особенных трудностей, но высокая собственная частота воспринимающей системы преобразователя достигается нелегко.
Насадок должен обладать возможно большей чувствительностью, линейностью характеристик в области измерения, стабильностью во времени, допускать температурную компенсацию « иметь минимальные габариты В целом измерительная система должна допускать одновременные измерение и фиксацию различные параметров в нескольких точках для выявления в1ременной связи между ними, быть по возможности простой в эксплуатации и нечувствительной к механическим, тепловым и электрическим внешним воздействиям.
Основная трудность в создании подобной аппаратуры заключается в удовлетворении всех или во всяком случае большинства этих требований. Для измерения в ядре потока быстроперемечных давлений полного торможения, статических давлений и углов в МЭИ разработана серия малоинерционных насадков с тензометрическими преобразователями, один из них изображен на рис. 10-11.
Собственно насадком такого прибора а является короткая трубка полного торможения. Преобразователь давления в э. д. с. расположен в малогабаритной коробке 1 обтекаемой формы, укрепленной на линзовой державке. Пульсирующее измеряемое давление подводится под мембрану 2, на обратной стороне которой намотан спиральный тензометрический датчик сопротивления 3.
Диаметр слюдяной мембраны — около 5 мм, толщина 0,012—
0,050 мм Спиральный тензометрический датчик диаметром 3 мм намотан из константановой проволоки 0 0,03 мм и имеет сопротивление —-100 ом. Тензодатчик включен в мостовую вводную схему измерительного устройства, .состоящего из стабилизированного блока питания, электронного многоканального усилителя и осциллографа.
Описываемые насадки с тензопреобразователями имеют вполне удовлетворительные характеристики. Это иллюстрируется приведенной на рис. 10-11,6 осциллограммой, полученной на специальной та-рцровочной установке, дающей тузядаеидальные импульсы давления разных 'величины и частоты.
Как указывалось выше, одной из важнейших характеристик насадка с преобразователем является собственная частота колебаний упругой системы.
Повышения собственной частоты преобразователя и увеличения его относительной чувствительности можно достигнуть, заменив тензометрический принцип измерения деформации мембраны емкостным, не требующим расположения на мембране какой-либо дополнительной массы.
| 1 |
( | 1 | ||
| а) 1 |
V/, | |||
| •*—ФЗ— _да~5_ | ||||
В МЭИ разработаны образцы малоинерционных насадков с емкостными преобразователями. Принципиальная схема преобразователя ясна из рис. 10-12. Подвижным электродом преобразователя служит слюдяная мембрана 1, покрытая тонким слоем алюминия. Неподвижный электрод 2 тщательно изолирован от корпуса. Рабочий диаметр мембраны 5 мм. Усилительную алектронную схему удобно располагать непосредственно на державке насадка, так как это избавляет от погрешностей, возникающих из-за переменной емкости соединительных проводов.
ЛЛЛЛЛЛЛЛ/
6)
Рис. 10-11. Тензометрический насадок для' измерения давления торможения и результаты тарировки.
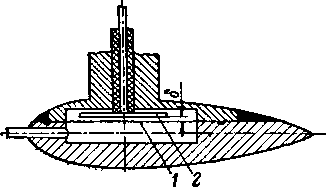
Рис. 10-12. Насадок с емкостным рреоб разователем.
Для измерения переменных давлений на поверхностях обтекаемых тел весьма широко применяются индуктивные преобразователи.
Несмотря «а относительную сложность их конструкции» они удобны тем, что при соблюдении определенных условий могут ра-богать непосредственно ла шлейф осциллографа без электронных усилителей.
Индуктивные преобразователи позволяют измерять как постоянную, гак и переменную составляющие давления и особенно удобны в случае необходимости многоточечных дистанционных измерений.
С
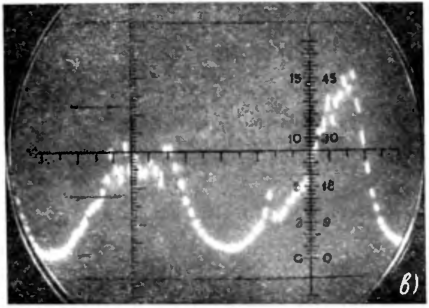
Рис 10-13. Насадок электротермоанемометра (а), его принципиальная электросхема (б) и осциллограмма пульсаций скорости (в).
а)
б)
В настоящее время наиболее разработанным методом исследования нестационарных газовых течений является термоанемометрия Современная термоанемометрическая установка, позволяющая определять пульсацию скорости, величину и направление скорости и температуру исследуемого потока, является довольно сложным комплексом, состоящим из нескольких насадков, измерительного моста, специального электронного усилителя и осциллографов.
Насадок термоанемометра (рис. 10-13,al) состоит из тонкой (0 0,01 -н0,02 мм) платиновой или вольфрамовой проволоки 1, приваренной к двум никелевым держателям 2, являющимся токопро-водами.
Существуют две основные принципиальные схемы измерительной системы термоанемометров. В обоих случаях насадок R„ (рис. 10-13,0) включается в одно из плен моста, остальные плечи которого выполнены из сопротивлений, не зависящих от температуры.
Сбалансированный при с=0 мост разбалансируется при введении насадка в поток с некоторой скоростью с Баланс моста можно восстановить либо увеличением тока при помощи реостата R$, либо компенсацией изменения сопротивления RH при помощи R2.
Первый метод — «постоянного сопротивления». Более распространен второй метод—постоянного тока.
При измерениях в нестационарных потоках в измерительную диагональ включается электронный усилитель со специально подбираемой характеристикой, поз!Воляющей в определенных пределам компенсировать тепловую инерцию нити
Тер1Моанемометры допускают проведение экспериментов в широком диапазоне скоростей и частот пульсаций газовых потоков.
10-3. ОПТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ГАЗОВЫХ
ПОТОКОВ
При больших скоростях в поле газового потока возникают значительные градиенты плотности. Неоднородность потока при этом позволяет широко щрименять оптические методы исследования. В некоторых случаях неоднородности поля создаются в потоке искусственно путем местного нагрева. При таком способе визуализации оптические методы могут быть применены и для дозвуковых потоков небольших скоростей.
Оптические приборы основаны на использовании известных свойств световых лучей, отклоняющихся от первоначального направления при пересечении ореды переменной плотности и, следовательно, переменной преломляющей способности.
Если п — показатель преломления световых лучей в данной точке поля, то значение плотности потока в точке определяется по соотношению
1 п2 —• 1
р п2 -+- 2 = const’
которое может быть заменено приближенным выражением: п — 1 п, — 1
-=-= const, (Ю-1)
Р Pi '
Где /ij, р! — показатель преломления и плотность в некоторой начальной точке; обычно эти величины относятся к нормальным атмосферным условиям (^,=0°С и рг = = 760 мм рт. ст.).
Из формулы (10-1) следует, что поле плотностей потока будет опрещелено, если опытным путем найти поле показателей преломления световых лучей в иослещуемой области. Давления и температуры могут быть определены, если известны еще два уравнения, связывающие параметры течения р, р и Т. Для этой цели служат уравнение состояния и уравнение изоэнтропического процесса.
Дифференцирование уравнения (10-1) приводит к очевидным соотношениям:
дп др дп др
ду ^ду ’ дг ^дг
и
д2п д2р дгп д2р
ду2 ^ dy2 ’ дг2 ^ дг2 ’
где К — постоянная величина.
Отсюда заключаем, что в зависимости от принципа действия и схемы оптигеские приборы могут быть использованы для непосредственного измерения плотности или первой или второй производной р. Для качественного изучения потока пригодны все приборы вне зависимости от того, каким методом определяется поле плотностей при количественном исследовании. Однако четкость и наглядность получаемой качественной картины потока, а также точность и трудоемкость обработки результатов качественного анализа существенно зависят от схемы и конструкции прибора.
Наиболее простыми являются оптические системы, в которых используется теневой метод определения плотностей. Схема такого устройства приведена на рис. 10-14,а Расходящийся пучок света от источника 5 проходит через линзу L и становится параллельным. Параллельный пучок лучей пересекает воздушный поток, в котором находится модель Л, и падает на экран или фотопластинку J. При об -текании модели возникают градиенты плотности. Так, например, если линия тока 1—2 пересекает головной скачок у модели, то плотность в зоне пересечения изменяется скачкообразно (рис. 10-14,6). При др д2р этом ?#0и?2#0.
В тех точках поля, где ]> 0, лучи параллельного пучка рас-
ходятся и на экране образуется темная область. Там, где 0,
лучи сходятся и освещенность на экране увеличивается. В точке 1 рис. 10-14,6) d2p/dz2 > 0, а в точке 2 d2p/dz2 С 0. Отсюди следует, что изображение головной волны у модели будет состоять из двух расположенных рядом линий: черной и белой. В простейшем случае теневой метод может быть осуществлен в расходящемся пучке света (без линзы). Этот метод, наиболее простой и дешевый, на ХОДИ'1’ применение при изучении скачков в потоке.
Другой, более чувствительный и точный оптический прибор, позволяющий измерять первые производные плотности, основан также на теневом методе. В этом приборе лучи, прежде чем попасть на экран, фокусируются в точку, к которой подводится нож При наличии неоднородности в потоке точка фокусировки части лучей сместится и попадет на нож, который не препятствует их
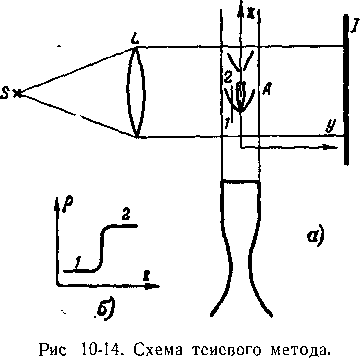
дальнейшему распространению. В результате картина, образующаяся на экране, будет иметь большую контрастность, чем в простом приборе (рис. 10-14).
Широкое распространение получили зеркальные системы теневых оптических приборов. Наиболее совершенным является прибор с зеркально-менисковой системой, предложенной проф. Д. д Максутовым (рис. 10-1S). От источника пучок света проходит через конденсор К и щель D. Плоское диагональное зеркало 5, изменяет направление хода лучей. Лучи попадают на вогнутое сферическое зеркало S2, преобразующее расходящийся пучок света в параллельный. Сферическое зеркало 52 вместе с рассеивающей менисковой линзой Lt образует зеркально-менисковую систему.
Эта часть прибора, состоящая из осветительного узла, зеркала 52 и линзы Li, создает параллельный пучок света и 'называется
коллиматором.
Приемную часть прибора составляют- менисковая линза L3, сферическое зеркало S3, плоское диагональное зеркало S4, нож Я, поворотное зеркало S5, экран I и фотоприставка Ф. Поворотное зеркало S0 в осветительном узле служит для контроля фокусировки щели
Для того чтобы источник света, который должен находиться «а сютичеакой оси системы, не закрывал центра поля изображения, оптическая ось системы смещена к ее краю Поэтому система несимметрична относительно геометрической оси, что хорошо видно на рис 10 15
Основное достоинство зеркально-менисковой системы заключается в том, что при одинаковой светосиле она -имеет значительно меньшие сферические и хроматические аберрации по сравнению с линзовой системой
Таким образом, в рассматриваемой схеме основными узлами являются крупная оптика прибора (зеркально менисковая), осве
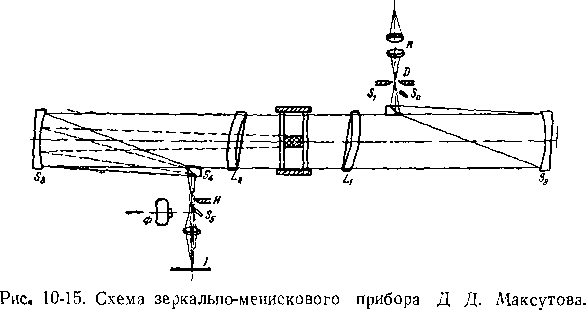
тительный узел, включающий механизм перемещения и изменения щели и фокусировки источника света и механизм перемещения ножа с фотаприставкой
В процессе эксперимента работа с прибором сводится к воздействию иа осветительный узел, на механизм перемещения щели, на фотоприставку и на механизм перемещения ножа.
В качестве источника света могут быть применены различные осветители, в том числе ртутная лампа, кинопроекционная лампа, искровой разрядник и пр. В ряде случаев оказывается целесообразным последовательное использование двух осветителей.
При качественном исследовании потока основная задача заключается в правильном выборе степени освещенности поля, которая зависит от размеров щели, положения ножа и типа осветителя Наибольшая освещенность получается при максимальной щели и выведенном яоже
Необходимо, однако, учитывать, что с увеличением освещенности чувствительность прибора уменьшается. [Поэтому область потока с небольшими градиентами плотности следует фотографировать при небольших размерах щели и введенном ib пучок света ноже Если основной интерес представляет исследование системы скачков, то размеры щели увеличиваются
Существенное значение-имеет также расположение ножа относительно изучаемого объекта В зависимости от положения ножа (горизонтальное, вертикальное или диагональное) лучи, прошедшие неоднородное поле и отклонившиеся, могут быть задержаны еожом или, наоборот, проходят к экрану. В первом случае яеоднородность получается на экране тамно-й, а во втором — светлой. Четкость изображения при этом сохраняется одинаковой. Лучшие результаты получаются тогда, когда кромка ножа расположена нормально к направлению максимального градиента плотностей.
Таким образом, тип осветителя, размер щели и положение ножа необходимо в каждом отдельном случае находить подбором
в зависимости от режима по-
тока, объекта и задачи исследования.
При количественном исследовании потока нож оказывается непригодным, так как он задерживает лучи и не позволяет измерить углы отклонения, необходимые для определения поля коэффициента преломления. В этом случае диафрагмирование пучка света производится тонкой иитью Такой метод количественного исследования с помощью опти-ческого прибора получил на-L _|”7_3 звание метода нити и щели.
ЦЦд.-Д Для непосредственного из
мерения поля плотностей потока применяется оптический прибор, известный под названием интерферометра. Принцип действия интерферометра можно уяснить из рассмотрения схемы, приведенной на рис. 10-16
Прибор состоит из двух отражательных зеркал Si и S2 и двух полупрозрачных зеркал и Я2, расположенных в углах прямоугольника под углом 45°. Рассмотрим вначале случай, когда ловерхиости зеркал строго параллельны. Расходящийся пучок света от источника 5 проходит через линзу L и становится параллельным. Лучи параллельного пучка раздваиваются при прохождении полупрозрачного зеркала П\. Часть лучей АСЕ' проходит через полупрозрачное зеркало Я, и, отражаясь от зеркал Si и Я2, попадает на экран Э в точке I. Другая часть лучей отражается от Я1 и S2 и, пройдя зеркало Я2> попадает в ту же точку экрана / (траектория этого луча—АЕА'С'1). Отражение лучей будет происходить также в-точках С и В (лучи СВ и BD) и С' я В' (лучи С'В' и B'D') полупрозрачных зеркал. Эти лучи приходят ,на экран в точке К. Следовательно, часть лучей, идущих в точку 1, пересекает полупрозрачные зеркала №, Я2) одни раз, а та часть, которая попадает в точку К, пересекает Яi или Я2 дважды. При этом в точке К сила света будет меньшей.
Т I К
Рис. 10-16. К пояснению принципа действия интерферометра.
Так как все четыре зеркала имеют параллельные поверхности,
•ро длина оптического пути (произведение траектории луча на показатель преломления) обоих пучков, идущих в точку /, будет одинаковой. В этом случае экран будет освещен равномерно.
Характер освещенности экрана резко меняется, если зеркала (Si или S2) повернуты на некоторый небольшой угол относительно оси, перпендикулярной плоскости чертежа. При этом изменяется длина оптического пути одного из пучков лучей, отраженных соответствующим зеркалом Si или S2 и идущих в точку 1. В результате происходит интерференция лучей, встречающихся в точке 1, заключающаяся в том, что часть лучей гасит друг друга и ка экране образуются перемежающиеся темные и светлые полосы ', расположенные на некотором одинаковом расстоянии Й одна от другой (рис. 10-17,а).
а)
Если между зеркалами Я( и Si будет помещено исследуемое поле R, плотность в котором р отличается от плотности среды между Я2 и S2, то благодаря изменению оптического пути луча СЕ' разность хода лучей СЕ' и ЕА' изменится. При этом полосы интерференции сместятся на некоторое расстояние параллельно самим себе (рис. 10-17,6).
Величина смещения полос интерференции определяется по уравнению
1(п' — 1) р — р'
(10-4)
е =
V р'
где I и I' — длины оптического пути луча в средах с плотностями соответственно р И р'.
Отсюда получаем разность плотностей:
Рис. 10-17 Схематическое изображение интерференционного спектра.
р - р' = т 2-
где m = 'i
— величина,
завчсящая от
условий
эксперимента:
угла поворота зеркал, плотности р' и коэффициента преломления среды п'
Величины (я, 5 и Q определяются в ходе эксперимента.
В тех случаях, когда исследуемое поле характеризуется неравномерным распределением плотностей, смещение полос интерференции будет различным ча разных участках экрана; в результате полосы будут искривлены. При этом линии одинаковых смещений полос интерференции (|/Я=const) отвечают линиям постоянной плотности (р — p'=const) в исследуемой области. Та^м образом, принцип действия интерферометра основан «а измерении разностей длин оптических путей света. Интерференционный метод позволяет детально аюследова+ь структуру потока в межлопаточных каналас? решеток и с достаточно высокой точностью определять количественные характеристики во всех тачках поля потока.
С помощью интерферометра легко установить изменение толщины пограничного слоя вдоль профиля, а также положение точек отрыва слоя. Этот прибор позволяет раздельно определять потери трения, кромочные и волновые потери в плоских решетках.
В качестве примера на рис. 10-18 приведен интерференционный
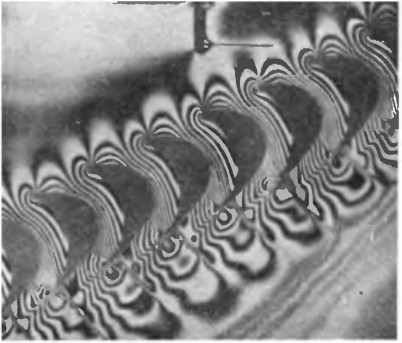
Рис. 10-18. Интерференционный 'снимок течения газа в турбинной решетке (опыты ЦКТИ).
снимок тотока в турбинной .решетке. Сравнение картин распределения давлений по профилю, полученных пиевмометрическим и интерференционным методами, показывает хорошее совпадение результатов оптических измерений с данными непосредственных измерений.
Схема интерферометра путем .небольшого дополнения позволяет одновременно получать интерференционные и теневые фотографии спектров потока. С этой целью в схему прибора можно ввести еще одно полупрозрачное зеркало Я3 (рис. 10-16). Тогда часть лучей, отраженных зеркалом П3, даст на экране в точке Т теневое изображение спектра. Другая часть лучен, пройдя через зеркало Я3, отразится зеркалом Я2 так же, как и в обычной схеме прибора.
10-4. УСТАНОВКИ ДЛЯ ИССЛЕДОВАНИЯ РЕШЕТОК В СТАТИЧЕСКИХ УСЛОВИЯХ
Испытания неподвижных решеток выполняются на установках различных типов, схема и конструкция которых определяются задачами .исследования и принятой методикой эксперимента.
Испытания в статических условиях, как уже указывалось, производятся с целью сравнительной оценки решеток и для изучения особенностей физического процесса обтекания различных решеток. Получаемые опытные характеристики в некоторых случаях могут быть использованы и для теплового расчета ступени.
Для определения характеристик и .для ‘исследования структуры потока в решетке используются различные 'методы аэродинамического эксперимента. К 'Ним относятся:
A. Методы изучении спектра потока, включающие: 1|) измерения поля потока .в характерных сечениях решетки насадками, а также различными электрическими приборами, фиксирующими полное и статическое давление, температуру полного торможения, направление скорости в точке; 2) изучение поля плотности оптическими методами (теневыми и интерференционными); 3) визуализацию потока путем подмешивания инородных частиц.
Б. Методы изучения потока у границ профиля, в том числе: 1) -измерение температур и давлений на поверхности профиля лопатки путем дренирования; 2) изучение профиля скоростей в попран'вчнам слое с помощью 1мшфотрубки или электрических приборов; 3) визуальное исследование структуры пограничного слоя на профиле путем окрашивания поверхности лопатки.
B. Методы взвешивания, включающие: 1|) определение суммарного импульса потока за решеткой; 2) определение сил, действующих на решетку в целом и «а отдельную лопатку в бесконечной решетке, с помощью специальных весов.
Г. Методы изучения нестационарных процессов, связанных с обтеканием отдельной лопатки или решетки. Исследуются колебания обтекаемого профиля, а также пульсации скоростей, давлений и температур обтекающего потока.
. Не останавливаясь .на сравнительной оценке различных ¦методов исследования, отметим, что одновременное их использование в одной установке представляется нерациональным. Осуществление такого требования делает установку хотя -и универсальной, ио конструктивно слишком сложной, дорогой и неудобной в эксплуатации.
Следует учитывать, что к схеме и конструктивному оформлению установки предъявляются дополнительные требования, обусловленные конструктивными параметрами исследуемых решеток и газодинамическими параметрами потока перед решеткой и за нею. Так, в исследуемой решетке могут изменяться: форма профиля, шаг и высота лопаток, угол их установки.
Важнейшими газодинамическими параметрами являются: угол входа потока на решетку, изменение которого должно предусматриваться в любой установке, скорость потока за решеткой М2 (или на входе в решетку Mi) число Re. При этом в ряде случаев представляется необходимым обеспечить раздельное изучение влияния сжимаемости и вязкости на характеристики решетки путем независимого изменения чисел М и Re. Диапазон изменения режимов диктуется в конечном итоге заданными условиями эксперимента и требованиями практического моделирования.
К числу последних, кроме очевидных условий M=idem и Re=idem, относятся специальные требования к организации потока перед решеткой. В некоторых случаях оказывается необходимым вводить искусственную цурбулизацию потока, в других - тщательно выравнивать пОгок на входе, а также обеспечивать условия обтекания бесконечной решетки.
Изложенное выше доказывает, что принципиальные схемы и конструктивные формы установок для статических испытаний решеток можно классифицировать по объектам исследования (установки для испытания плоских или цилиндрических решеток), по условиям испытания решеток (установки с открытой рабочей частью или с камерой противодавления для испытания в равномерном или
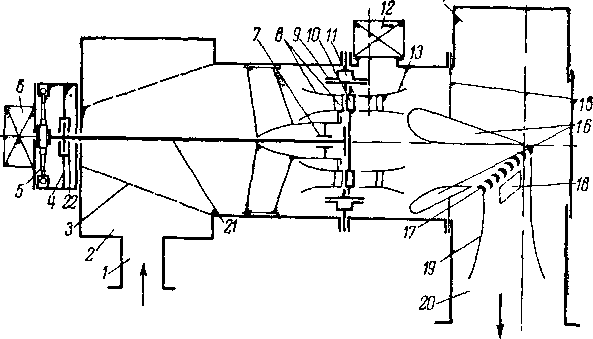
Рис. 10-19. Принципиальная схема аэродинамической трубы для статического исследования плоских и кольцевых решеток. !—по\воч воздуха; 2—кольцевая камера; 3—сетка; 4 — измеритель Р0; 5— измеритель Мкр;'6—тарировочное устройство; 7—подшипник; 8 и 13—обечайка; 9—11— \плотнение; 10—исслед-\емая решетка; 12—коораинатник; ' 14 и 20 —вы" хлопная камера; /5—съемный фланец; 1Ь — сопло птоского пакета; 17—плоский пакет; 18— поле координат ника; 19— дифф130р; 21 — вал; 22 —упорный подшипник.
турбулиаиро'ванном дозвуковом или оверхвузковом потоке иа входе) и по принятой методике исследования (установки для детального изучения аэродинамических полей, для определения усилий, действующих на профиль iB решете, для исследования решеток оптическими методами и т. п.).
Установки можно классифицировать также в зависимости от применяемого рабочего тела (паросые, «оадушные, паровоздушные и др.) и способа организации рабочего потока (установки с избыточным или атмосферным давлением на входе, эжекторные установки, паровые установки, работающие на конденсатор).
Лабораторные стенды должны, как правило, включать несколько экспериментальных установок. При этом крут задач, решаемых «а каждой установке, ограничен ее конструкцией, Принятой методикой исследования и предельными значениями параметро® рабочего тела.
Рассмотрим принципиальные схемы некоторых испытательных установок. На рис. 10-19 приведена схема аар динамической трубы,
в которой предусмотрена возможность простой смены рабочих частей. Воздух от компрессора подается в трубу через патрубок 1 и попадает в кольцевую камеру 2. Пройдя через конус 3, имеющий большое число отверстий, воздух попадает в ресивер и обтекает исследуемую кольцевую решетку 10. Нужное направление потока на входе в исследуемую решетчу создается обечайкой с направляющей решеткой 8.
Исследуемый кольцевой пакет крепится к фланцу вала 21, установленного в шариковых опорном подшипнике 7 и опорно-упорном 22. Осевое усилие через подшипник 22 передается на упругий элемент 4, а крутящий момент с вала на корпус передается через симметричные упругие элементы 5. На iyinpyrne элементы наклеены проволочные тензодатчики, ери помощи которых с достаточной точностью определяются крутящий момент и осевое усилие.
Решетка 10 снабжена уплотнением 9, в камеру // которого подается воздух под давлением, .равным давлению в ресивере. Таким образом, перетекание из ресивера в выхлопную камеру устраняется и расход, прошедший через решетку 10, равен измеренному расходу через патрубок 1. Такое определение расхода необходимо при применении метода взвешивания. Для повышения точности измерения Мкр и Ра предусмотрено специальное тарировочное устройство 6
Для исследования поля потока перед решеткой и за нею используются насадки, перемещаемые автоматизированным коорди-натником 12.
При исследовании кольцевой решетки фланец 15 отсутствует и воздух сбрасывается в выхлопную коробку 20.
При необходимости исследований решеток в плоском пакете кольцевой пакет 10, обечайки 8, 13 и уплотнение 9 удаляются. Устанавливается фланец 15, а на него — плоская рабочая часть нужной конструкции с соплом 16, исследуемой решеткой 17, коор-динатником 18 и диффузором 19.
Рабочие части для исследования плоских пакетов имеют различное конструктивное оформление. На рис. 10-20 /приведен общий вид одной из рабочих частей для плоских решеток.
Здесь верхняя стенка сопла 5 болтами 6 неподвижно крепится к корпусу 3 так, что ее выходная кромка совпадает с общей осью двух дисков 8, 0 Диски 8 с помощью сухарей 7 неподвижно и соосно скреплены между собой. Нижняя стенка сопла 4 скользящими шпонками 10 и винтами 11 крепится к вертикальному ползуну /, скрепленному с корпусом 3 винтом 2.
Перемещая стенку 4 относительно ползуна 1 и ползун — относительно корпуса 3, можно изменять расстояние ОС в пределах ОБ при заданном угле входа в зависимости от длины исследуемого пакета. Изменение угла входа производится поворотом дисков 8 относительно корпуса 3.
Коордииатник за решеткой, жестко скрепленный с дисками 8, обеспечивает четыре независимых перемещения насадка: лииейиые перемещения в направлениях осей xyz и поворот вокруг оси z
Три из этих перемещений (в направлениях * и z и поворот вокруг оси z), осуществляются электродвигателями, дистанционно управляемыми оператором по заданной программе.
На установках рассмотренного типа решетки могут быть испытаны в равномерном или турбулизированном потоке. С целью искусственной гурбулизации потока в параллельном участке перед решеткой можно расположить турбулизирующие сетии. В зависимости от густоты сетки (размеров ячеек) и диа.метра проволоки при неизменной скорости потока может быть получена различная степень турбулентности перед решеткой.
Наряду с раюомотремньши схемами установок, работающих с избыточным давлением, находят применение схемы с атмосфер-
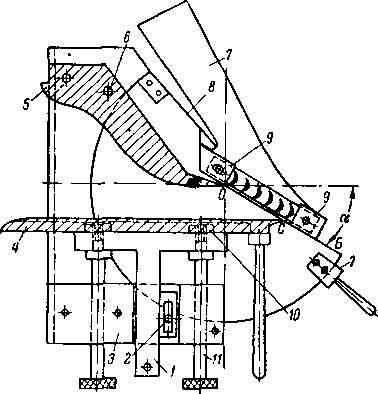
Рис. 10-20. Плоская рабочая часть с переменной длиной пакета и автоматическим коор-динатником (продольный разрез).
1 — ползун; 2, 6 и // — винт; S—корпус; 4 и 5 — соп* ло; 7—сухари; 5—диск; 0—крепление пакета; 10 —
шпонка.
ным давлением в форкамере, в том числе установки эжекторного типа. В таких установках воздух засасывается в форкамеру из атмосферы, ускоряется в сопле и направляется к ре ненке. Поток в решетке индуцируется эжектором. Такая установка работает с незамкнутым потоком м позволяет получить низкие давления за решеткой (и соответственно низкие числа Re).
Приведенный краткий обзор показывает, что количество возможных схем установок для статических испытаний решеток достаточно велико. Выбор той или иной схемы определяется задачами эксперимента, причем в основу сравнения различных схем должны быть положены соображения экономичности и требования теории моделирования.
Имея в виду принятые ранее обозначения, можно записать выражения для чисел М и Re в известном виде: где L — характерный линейный размер; р, Т, с — параметры потока в рабочей части установки (за решеткой).
![]()
а |/ kgR , _
с
Из выражений для М и Re исключим скорость с; тогда
![]()
(10-5)
Обозначим Ку коэффициент качества установки, определяемый как отношение мощности потока к потребной мощности компрессора в рабочем сечении установки. Потребная мощность компрессора определяется по формуле
Nk = K
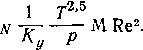
(10-6)
В уравнениях (10-5) и (10-6) KL и KN являются постоянными величинами.
Из формулы (10-6) следует, что при одинаковых параметрах газа (р « Т) габариты установки в 'рабочем сечонии увеличиваются пропорционально отношению Re/M. С увеличением давления размеры [установки сокращаются. Мощность установки пропорциональна MRe2.
Повышение коэффициента качества установки Ку достигается путем введения диффузора, снижения потерь в установке и использования компрессора с высоким к. п. д. в пределах рабочих режимов.
С помощью формул (10-5) и (10-6) можно сравнить две принципиально различные схемы установок: с избыточным и атмосферным давлением в форкамере.
При соблюдении подобия одновременно по М и Re мощность установки с атмосферным давлением получается значительно больше [мощности установки с избыточным давлением Вместе с тем в первом случае размеры исследуемых моделей также возрастают, что особенно важно при исследовании пограничного слоя в решетке. Установки с избыточным давлением могут работать с камерой противодавления и с открытой рабочей частью. В последнем случае техника эксперимента значительно упрощается.
Следовательно, в установках с избыточным [давлением можно осуществить раздельное исследование влияния сжимаемости и вязкости, в то время как в установках с атмосферным [давлением в форкамере раздельное моделирование неосуществимо. При малых значениях М экономичность обеих схем одинакова.
Таким образом, мы видим, что установки с избыточным давлением в форкамере в общем случае (подобие по М и Rej) обладают большей экономичностью и более универсальны. Они имеют поэтому более широкое распространение. В некоторых случаях, однако, установки с атмосферным давлением более экономичны (если исследуется влияние только -сжимаемости) и явлчютси единственно возможным решением. Только по такой схеме может, например, работать паровоздушная установка с паровым эжектором.
Опытное исследование характеристик турбинной или компрессорной ступени производится на специальных экспериментальных турбинах или компрессорах.
Стенд экспериментальной турбины состоит из турбины, электрического или гидравлического нагрузочного устройства, воздушной, паровой «ли паровоздушной тепловой схемы и специальной системы измерительных устройств.
В некоторых случаях турбина и нагрузочное устройство ко«-структивно объединяются. В установках большой мощности турбина я напрузочное устройство обычно выполнены отдельно и соединяются муфтой.
Общим и весьма важным требованием, предъявляемым к нагрузочным устройствам экспериментальныi турбин, является возможность максимально точного измерения крутящего момента на валу турбины. Желательной является возможность измерения осевого усилия ротора.
Экспериментальная турбина должяа обеспечивать возможность испытания ступеней с различными геометрическими размерами, надежную работу в широком диапазоне чисел оборотов, удобную и правильную расстановку измерительной аппаратуры и простоту монтажных работ.
Принципиально можно спроектировать универсальную экспериментальную турбину, обеспечивающую испытания как отдельных ступеней, так и групп их, работу с различными оборотами, (позволяющую испытывать модели регулирующих, промежуточных и по-следних ступеней. Однако конструкция и эксплуатация такой машины будут весьма сложными и создание ее едва ли целесообразно Очевидно, рациональнее иметь .несколько экспериментальных машин, каждая из которых ориентирована на исследование определенных типов ступеней.
На .рис. 10-21 в качестве примера приведен продольный разрез быстроходной экспериментальной воздушной турбины, предназначенной для детального исследования ступеней с относительно длинными лопатками (0 = d//=2,8-f-4,9). Турбина рассчитана на максимальный расход воздуха G = 4,5 кг\сек\ Г0 = 200°С при максимальном давлении р0 = 3 ата и «макс = 20000 об/мин.
Ресиверная часть турбины 1 сварная, без горизонтального разъема. Воздух через патрубок 2 подается в кольцевую камеру 3, откуда он через сверления 18 равномерно подводится в воздушную коробку 19. Для организации потока перед 'направляющей решеткой 22 служат обтекатели 20 и решетка пластин 21, позволяющая изменять угол входа в направляющую решежу. Корпус турбины 25 сварной с горизонтальным разъемом. Воздух, прошедший через рабочую часть, выбрасывается через выхлопной патрубок 37. Конструкцией предусмотрена работа машины в качестве экспериментальной турбины или аэродинамической трубы для исследования кольцевых решеток.
Конструкция позволяет взвешивать крутящий момент и осевое усилие как яа рабочем колесе, так и на направляющем аппарате.
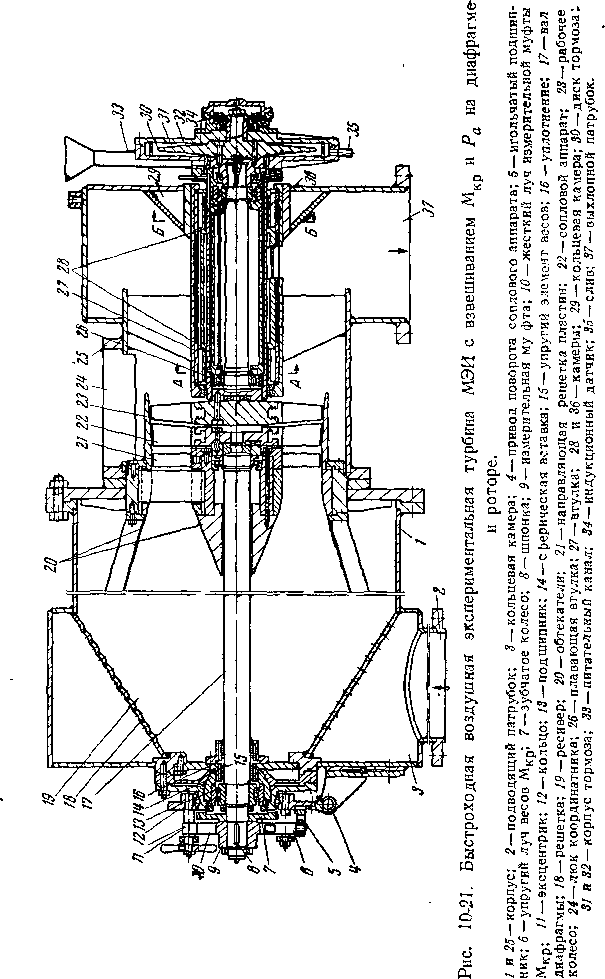
Последний укреплен на полом валу 17 Передний шариковыи поД* шипник вала не воспринимает осевой нагрузки Осевая налрузка воспринимается задним упорно-опорным подшипником 13 и через сферическую вставку 14 передается на упругий элемент 15
Крутящий момент через шпанку 8 передается на трехлучевую измерительную муфту 9, два упругих симметричных луча которой 6 предназначены для измерений крутящего момента и один жест кий 10— для тарировки измерительной муфты
Для того чтобы трение в контактах упругих лучей измеритель ной муфты не вносило погрешности в измерение осевого усилия, контакт осуществлен через игольчатый подшипник в сферическом корпусе 5 Крутящий момент передается через кольцо 12 на червячную пару 4 Для измерения крутящего момента и осевого уси-чия на диафрагме применяются электрические тензометры сопротивления, пакленные на гибкие элементы 6 и 15
Весовое устройство описываемой машины позволяет легко про водить тарировки в процессе эксперимента, а при необходимости — перед каждым измерением
При необходимости параллельно с электротензометрами для измерения Л4кр и Ра могут применяться высокоточные механические или оптико-меччнические индикаторы
Рабочее колесо 23 экспериментальной турбины выполнено с фтанцевым креплением Вал — гибкий, вращающийся в специальных прецизионных подшипниках качения Нагрузочное устройство— однодисковый гидротормоз консочьной конструкции
Специфическим для экспериментальных турбин является вопрос об измерении момента трения в подшипниках В ряде существую щих машин момент в подшипниках вообще не измеряется и в расчет вводится поправка, полученная на основании тарировки Однако цля точных экспериментальных турбин такой метод является недо пустимым, так как момент в упорном подшипнике зависит от осевой нагрузки, а следовательно, и от режима работы турбины
В экспериментальной турбине (рис 10-21) корпуса опорного и опорно-упорного подшипников размещены в разъемной «плавающей» втулке 26 В неразъемной и неподвижно связанной с корпусом втулке 27 в сечениях АА и ББ выполнено по четыре симметричные камеры 28, питаемые через дроссельные шайбы сжатым воз дулом с давлением~6 ата из кольцевой камеры 29 В рабочих условиях из-за разности зазоров между втулками 26 и 27 вверху и внизу давление в верхних камерах 28 будет меньше давления в нижних камерах 36 Разность давлений, направленная вверх, при определенных условиях уравновесит силу веса конструкции, заклю ченной во втулке 26, и заставит ее «всплыть»
Основной нагрузочный момент с диска гидротормоза 30 передается на корпус гидротормоза 32, жестко связанного с «плавающей» втулкой 26 Поэтому моменты подшипников и налрузочпый момент диска тормоза суммируются и уравновешиваются моментом весового устройства, приложенным к корпусу 32 Таким образом, весовое устройство измеряет сумму трех моментов момента опорного подшипника, момента опорно упорного подшипника и момента на диске гидротормоза Момент, развивающийся в результате трения диска 23 о воздух, весами не учитывается, но с необходимой точностью может быть определен путем тарировки
Осевое усйлие рабочего колеса, Передаваемое На «плавающую» втулку через опорно-упорный подшипник, измеряется специальной весовой головкой
Вода в гидротормоз подается открытой спруей в питательный канал 33 и удаляется через сливной вентиль 35 Счетчик оборотов, тйхометр и автомат безопасности ib описываемой машине — электрические, работающие от общего индукционного датчика 34
Для измерения аэродинамических полей за колесом или направляющим аппаратом при работе без колеса применяется специальный координатнчк с автоматическим эчектроприводом, устанавливаемый в люке 24
1. Таблицы газодинамических функций для ? = 1,4 и ?=1,3
2. Диаграммы скачков уплотнения для ? = 1,3 и ?=1,4
¦о
сл
4*
ПРИЛОЖЕНИЯ
ГАЗОДИНАМИЧЕСКИЕ ФУНКЦИИ ДЛЯ ?=1,4
| X | Р Ро |
_Р_ Ро | Т То | Q |
а ~<*7 | ? | Jo | ф(Х) |
“т | 5 |
м |
| 0,02 |
0,9998 | 0,9998 |
0,9999 | 0,0315 |
1,0954 | 0,00816 |
0,0002 | 50,02 | 0,0182 | ||
|
0,04 | 0,9990 |
0,9993 | 0,9997 |
0,0631 | 1,0953 |
0,0163 | 0,0009 |
25,04 | _ |
_ | 0,0265 |
| 0,06 | 0,9979 |
0,9985 | 0,9994 |
0,0945 | 1,0951 |
0,0245 | 0,0021 |
16,72 | _ |
0,0548 | |
| 0,08 |
0,9963 | 0,9974 |
0,9993 | 0,1259 |
1,0949 | 0,0327 |
0,0037 | 12,58 |
_ | _ |
0,0731 |
| 0,10 |
0,9941 | 0,9958 |
0,9983 | 0,1571 |
1,0945 | 0,0408 |
0,0058 | 10,10 |
_ | _ |
0,0914 |
| 0,12 |
0,9916 | 0,9940 |
0,9976 | 0,1882 |
1,0941 | 0,0490 |
0,0083 | 8,453 |
— | — |
0,1097 |
| 0,14 |
0,9886 | 0,9919 |
0,9967 | 0,2190 |
1,0936 | 0,0571 |
0,0113 | 7,282 | 0,1280 | ||
|
0,16 | 0,9851 |
0,9893 | 0,9957 |
0,2497 | 1,0931 |
0,0653 | 0,0148 |
6,410 | _ |
_ | 0,1464 |
| 0,18 | 0,9812 |
0,9865 | 0,9946 |
0,2801 | 1,0925 |
0,0735 | 0,0186 |
5,736 | _ |
__ | 0,1648 |
| 0,20 | 0,9768 |
0,9834 | 0,9933 |
0,3102 | 1,0918 |
0,0816 | 0,0229 |
5,200 | _ |
__ | 0,1832 |
| 0,22 | 0,9720 |
0,9799 | 0,9919 |
0,3401 | 1,0910 |
0,0898 | 0,0277 |
4,765 | _ |
_ | 0,2016- |
| 0,24 | 0,9668 |
0,9762 | 0,9904 |
0,3696 | 1,0902 |
0,0980 | 0,0328 |
4,407 | — | - | 0,2201 |
| 0,26 | 0,9611 | 0,9721 | 0,9887 | 0,3987 | 1,0893 | 0,1061 | 0,0383 | 4,106 |
0,2387 | ||
| 0,28 | 0,9550 |
0,9667 | 0,9869 |
0,4274 | 1,0883 |
0,1143 | 0,0442 |
3,851 | 0,573 | ||
| 0,30 |
0,9485 | 0,9629 |
0,9850 | 0,4557 |
1,0872 | 0,1225 |
0,0505 | 3,633 |
_ | 0,2759 | |
| 0,32 | 0,9415 |
0,9579 | 0,9829 |
0,4835 | 1,0861 |
0,1306 | 0,0572 |
3,445 | _ |
_ | 0,2946 |
| 0,34 | 0,9341 |
0,9425 | 0,9807 |
0,5109 | 1,0848 |
0,1388 | 0,0642 |
3,281 | _ |
0,3134 | |
| 0,36 |
0,9264 | 0,9469 |
0,9784 | 0,5377 |
1,0835 | 0,1470 |
0,0716 | 3,138 |
— | — |
0,3322 |
| 0,38 |
0,9183 | 0,9409 |
0,9759 | 0,5640 |
1,0822 | 0,1551 |
0,0793 | 3,012 | 0,3511 | ||
|
0,40 | 0,9097 |
0,9346 | 0,9733 |
0,5897 | 1,0807 |
0,1633 | 0,0872 |
2,90 | _ |
0,3701 | |
| 0,42 |
0,9008 | 0,9281 |
0,9706 | 0,6149 |
1,0792 | 0,1715 |
0,0955 | 2,801 | — | 0,3892 |
<л
•сп
| 0,44 | 0,8911 |
0,9213 | 0,9677 |
0,6394 | 1,0776 |
0,1796 | 0,1040 |
2,713 | ||
|
0,46 | 0,8819 |
0,9142 | 0,9647 |
0,6633 | 1,0760 |
0,1878 | 0,1128 |
2,634 | — |
-- |
| 0,48 |
0,8719 | 0,9067 |
0,9616 | 0,6865 |
1,0742 | 0,1960 |
0,1219 | 2,563 |
— | - |
|
0,50 | 0,8616 |
0,8991 | 0,9583 |
0,7091 | 1,0724 |
0,2041 | 0,1311 |
2,500 | — |
- |
| 0,52 |
0,8509 | 0,8911 |
0,9549 | 0,7309 |
1,0705 | 0,2123 |
0,1405 | 2,443 |
.— | - |
|
0,54 | 0,8400 |
0,8829 | ' 0,9514 |
0,7521 | 1,0685 |
0,2204 | 0,1502 |
2,392 | — |
- |
| 0,56 |
0,8287 | 0,8744 |
0,9477 | 0,7724 |
1,0664 | 0,2286 |
0,1599 | 2,346 |
_ | _ |
|
0,58 | 0,8171 |
0,8657 | 0,9439 |
0,7920 | 1,0643 |
0,2368 | 0,1699 |
2,304 | - |
- |
| 0,60 |
0,8053 | 0,8567 |
0,9400 | 0,8108 |
1,062 | 0,2449 |
0,1799 | 2,267 |
-- | - |
|
0,62 | 0,7931 |
0,8474 | 0,9359 |
0,8288 | 1,060 |
0,2531 | 0,1900 |
2,233 | - |
- |
| 0,64 |
0,7808 | 0,8379 |
0,9317 | 0,8460 |
1,057 | 0,2613 |
0,2002 | 2,202 | - | •- |
| 0,66 | 0,7681 | 0,8283 | 0,9274 | 0,8623 | 1,055 | 0,2694 |
0,2105 | 2,175 |
— | - |
| 0,68 | 0,7553 |
0,8183 | 0,9229 |
0,8778 | 1,052 |
0,2776 | 0,2207 |
2,151 | _ | * _ |
| 0,70 |
0,7422 | • 0,8082 |
0,9183 | 0,8924 |
1,050 | 0,2858 |
0,2310 | 2,129 |
- | - |
|
0,72 | 0,7289 |
0,7978 | 0,9136 |
0,9052 | 1,047 |
0,2939 | 0,2413 |
2,109 | -- |
- |
| 0,74 |
0,7153 | 0,7872 |
0,9087 | 0,9189 |
1,044 | 0,3021 |
0,2514 | 2,091 |
-- | — |
|
0,76 | 0,7017 |
0,7764 | 0,9037 |
0,9308 | 1,041 |
0,3103 | 0,2616 |
2,076 | - |
- |
| 0,78 |
0,6879 | 0,7655 |
0,8986 | 0,9418 |
1,038 | 0,3184 |
0,2717 | 2,082 |
- | - |
|
0,80 | 0,6738 |
0,7593 | 0,8933 |
0,9518 | 1,035 |
0,3266 | 0,2816 |
2,050 | _ |
_ |
| 0,82 |
0,6597 | 0,7429 |
0,8879 | 0,9610 |
1,032 | 0,3348 |
0,2914 | 2,039 |
- | - |
|
0,84 | 0,6454 |
0,7314 | 0,8824 |
0,9692 | 1,029 |
0,3429 | 0,3011 |
2,030 | - |
- |
| 0,86 |
0,6310 | 0,7197 |
0,8767 | 0,9764 |
1,026 | 0,3511 |
0,3105 | 2,023 |
- | - |
|
0,88 | 0,6165 |
0,7079 | 0,8709 |
0,9826 | 1,022 |
0,3593 | 0,3198 |
2,016 | - |
¦- |
| 0,90 | 0,6020 | 0,6959 | 0,8650 | 0,9880 | 1,019 | 0,3674 |
0,3'288 | 2,011 |
- | - |
|
0,92 | 0,5873 |
0,6837 | 0,8589 |
0,9923 | 1,015 |
0,3756 | 0,3376 |
2,007 | __ |
- |
| 0,94 |
0,5726 | 0,6715 |
0,8527 | 0,9956 |
1,011 | 0,3837 |
0,3461 | 2,004 |
- | - |
|
0,96 | 0,5579 |
0,6591 | 0,8464 |
0,9981 | 1,008 |
0,3919 | 0,3543 |
2,002 |
| X |
Р Ро | Р Ро | Т То | Я | а а» | ? |
/о | ф(Х) |
“т | Ъ | м |
| 0,98 |
0,5430 | 0,6465 |
0,8399 | 0,9995 |
1,004 | 0,4901 |
0,3626 | 2,0004 | 0,9761 | ||
|
1,00 | 0,5283 |
0,6339 | 0,8333 |
1,0 | 1,0 | 0,4082 | 0,3698 | 2,000 |
90° | 0 | 1,00 |
| 1,02 | 0,5135 | 0,6212 | 0,8266 | 0,9995 | 0,9960 | 0,4164 | 0,3770 | 2,0004 | 70°33' | 0°10' | 1,024 |
| 1,04 |
0,4987 | 0,6084 |
0,8197 | 0,9981 |
0,9918 | 0,4246 |
0,3838 | 2,0015 |
72°36' | 0°30' |
1,049 |
| 1,06 |
0,4840 | 0,5955 |
0,8127 | 0,9957 |
0,9876 | 0,4327 |
0,3903 | 2,0034 |
68°22' | 0°55' |
1,073 |
| 1,08 | 0,4693 | 0,5825 | 0,8056 | 0,9924 | 0,9832 | 0,4409 | 0,3963 | 2,006 |
65°33' | 1 °25' |
1,098 |
| 1 ,10 | 0,4546 | 0,5694 | 0,7983 | 0,9381 | 0,9788 | 0,4491 | 0,4019 | 2,009 |
62°5Г | Г 55' |
1,124 |
| 1,12 |
0,4400 | 0,5503 |
0,7909 | 0,9829 |
0,9742 | 0,4572 |
0,4071 | 2,013 |
60°26' | 2°25' |
1,150 |
| 1,14 |
0,4255 | 0,5432 |
0,7834 | 0,9768 |
0,9690 | 0,4654 |
0,4118 | 2,017 |
58° 15' | 2°55' |
1,176 |
| 1,16 |
0,4111 | 0,5300 |
0,7757 | 0,9698 |
0,9648 | 0,4736 |
0,4160 | 2,022 | 56° 15' | 3°30' | 1,202 |
| 1,18 |
0,3968 | 0,5168 |
0,7718 | 0,9619 |
0,9600 | 0,4817 |
0,4197 | 2,027 |
54°26' | 4° 10' |
1,229 |
| 1,20 |
0,3827 | 0,5035 |
0,7600 | 0,9531 |
0,9550 | 0,4899 |
0,4229 | 2,033 |
52°43' | 4° 50' |
1,257 |
| 1,22 |
0,3687 | 0,4903 |
0,7519 | 0,9435 |
0,9499 | 0,4981 |
0,4257 | 2,040 |
51 °08' | 5°35' |
1,284 |
| 1,24 |
0,3548 | 0,4770 |
0,7437 | 0,9331 |
0,9447 | 0,5062 |
0,4279 | 2,046 |
49°38' | 6° 15' |
1,313 |
| 1,26 |
0,3410 | 0,4638 |
0,7354 | 0,9218 |
0,9394 | 0,5144 |
0,4295 | 2,054 |
48°12' | 7°50’ |
1,341 |
| 1,28 |
0,3275 | 0,4505 |
0,7969 | 0,9097 |
0,9340 | 0,5226 |
0,4306 | 2,061 |
46°51' | 7° 55' |
1 ,370 |
| 1,30 |
0,3141 | 0,4373 |
0,7183 | 0,8968 |
0,9284 | 0,5307 |
0,4311 | 2,069 |
45°35' | 8° 45' |
1,400 |
| 1,32 |
0,3010 | 0,4241 |
0,7096 | 0,8832 |
0,9228 | 0,5389 |
0,4311 | 2,078 |
44°21' | 9°35' |
1,430 |
| 2,34 |
0,2880 | 0,4110 |
0,7007 | 0,8688 |
0,9170 | 0,5470 |
0,4305 | 2,086 |
43°11' | 10°30' |
1,461 |
| 1,36 |
0,2753 | 0,3980 |
0,6917 | 0,8538 |
0,9111 | 0,5552 |
0,4294 | 2,095 |
42°04' | 11 °30' |
1,493 |
| 1,3§ |
0,2628 | 0,3849 |
0,6826 | 0,8380 |
0,9050 | 0,6534 |
0,4276 | 2,105 |
40°59' | 12°25' |
1,525 |
| 1,40 |
0,2500 | 0,37ч20 | 0,6733 | 0,8216 | 0,8989 | 0,5715 | 0,4253 | 2,114 |
39°53' | 13° 15' |
1,557 |
| 1,42 | 0,2385 | 0,3592 | 0,6639 | 0,8045 | 0,8926 | 0,5797 | 0,4225 | 2,124 |
38°57' | 14° 10' |
1,591 |
| 1,44 | 0,2267 | 0,3464 | 0,6544 | 0,7869 | 0,8861 | 0,5879 | 0,4190 | 2,134 |
37°59' | 15° 15' |
1,625 |
. Дейч
| 1,46 |
0,2152 | 0,3338 |
0,6447 | 0,7687 |
0,8796 | 0,5960 |
0,4151 | 2,145 |
37°03' | 16° 15' |
1,660 |
| 1,48 |
0,2040 | 0,3212 |
0,6349 | 0,7499 |
0,8729 | 0,6042 |
0,4104 | 2,156 |
36°08' | 17°20' |
1,695 |
| 1,50 |
0,1930 | 0,3088 |
0,6250 | 0,7307 |
0,8660 | 0,6124 |
0,4053 | 2,167 |
35° 16' | 18°25' |
1.732 |
| 1,52 |
0,1823 | 0,2965 |
0,6149 | 0,7110 |
0,8590 | 0,6205 |
0,3996 | 2, 178 |
34° 25' | 1940' |
1,769 |
| 1,54 | 0,1720 | 0,2844 | 0,6047 | 0,6908 | 0,8519 | 0,6287 | 0,3934 | 2,189 |
33° 35' | 20°55' |
1 ,808 |
| 1,56 | 0,1619 | 0,2724 | 0,5944 | 0,6703 | 0,8446 | 0,6369 | 0,3867 | 2,201 |
32°47' | 22°02' |
1 ,847 |
| 1,58 | 0,1521 | 0,2606 | 0,5839 | 0,6494 | 0,8371 | 0,6450 | 0,3794 | 2,213 |
32°00' | 23° 11' |
1 ,887 |
| 1,60 | 0,1427 | 0,2489 | 0,5733 | 0,6282 | 0,8294 | 0,6532 | 0,3717 | 2,295 |
31014' |
24°22' | 1,929 |
| 1,62 | 0,1335 |
0,2374 | 0,5626 |
0,6067 | 0,8216 |
0,6614 | 0,3634 |
2,237 | 30°29' |
25°37' | 1,971 |
| 1,64 | 0,1249 |
0,2261 | 0,5517 |
0,5849 | 0,8137 |
0,6695 | 0,3547 |
2.250 | 29°45' |
26°48' | 2,015 |
| 1,66 | 0,1162 |
0,2150 | 0,5407 |
0,5630 | 0,8055 |
0,6777 | 0,3456 |
2,262 | 29°02' |
28°0Г | 2,061 |
| 1,68 | 0,1081 |
0,2041 | 0,5296 |
0,5409 | 0,7972 |
0,6859 | 0,3360 |
2,275 | 28°20' |
29°20' | 2,107 |
| 1,70 | 0,1002 |
0,1934 | 0,5183 |
0,5187 | 0,7887 |
0,6940 | 0,3261 |
2,233 | 27°38' |
30°30' | 2,155 |
| 1,72 | 0,0927 |
0,1830 | 0,5069 |
0,4964 | 0,7799 |
0,7022 | 0,3157 |
2,301 | 26°58' |
31 °50' | 2,205 |
| 1,74 | 0,0856 |
0,1727 | 0.4954 |
0,4741 | 0,7710 |
0,7103 | 0,3051 |
2,315 | 26° 18' |
32°48' | 2,257 |
| 1 ,76 | 0,0787 |
0,1627 | 0,4837 |
0,4518 | 0,7619 |
0,7185 | 0,2940 |
2,328 | 25°39' |
34°29' | 2,310 |
| 1,78 | 0,0722 |
0,1530 | 0,4719 |
0,4296 | 0,7525 |
0,7267 | 0,2828 |
2,342 | 25°01' |
35°49' | 2,365 |
| 1,80 | 0,0660 |
0,1435 | 0,4600 |
0,4076 | 0,7430 |
0,7348 | 0,2712 |
2,355 | 24°23' |
36°37' | 2,423 |
| 1,82 | 0,0601 |
0,1342 | 0,4479 |
0,3855 | 0,7331 |
0,7430 | 0,2595 |
2,369 | 23°45' |
38° 38' | 2,482 |
| 1,84 | 0,0546 |
0,1253 | 0,4357 |
0,3637 | 0,7231 |
0,7512 | 0,2475 |
2,383 | 23°09' |
40°00* | 2,544 |
| 1,86 | 0,0494 |
0,1166 | 0,4234 |
0,3423 | 0,7128 |
0,7593 | 0,2354 |
2,398 | 22°32' |
41 °32' | 2,609 |
| 1,88 | 0,0445 |
0,1082 | 0,4109 |
0,3210 | 0,7022 |
0,7675 | 0,2232 |
2,414 | 2Г56' |
43°04' | 2,677 |
| 1,90 | 0,0399 |
0,1001 | 0,3983 |
0,3001 | 0,6913 |
0,7757 | 0,2109 |
2,426 | 21°20' |
44°14' | 2,748 |
| 1,92 | 0,0356 |
0,0923 | 0,3856 |
0,2796 | 0,6802 |
0,7838 | 0,1985 |
2,441 | 20°45' |
45°47' | 2,823 |
| 1,94 | 0,0316 |
0,0848 | 0,3727 |
0,2595 | 0,6688 |
0,7920 | 0,1862 |
2,455 | 20° 10' |
47°43' | 2,901 |
| 1/96 | 0,0279 |
0,0776 | 0,3597 |
0,2400 | 0,6570 |
0,8002 | 0,1739 |
2,470 | 19°35' |
29°25' | 2,983 |
| 1,98 | 0,0245 |
0,0707 | 0,3466 |
0,2209 | 0,6449 |
0,8083 | 0,1617 |
2,485 | 19°01' |
51°46' | 3,070 |
|
X | р Ро |
р Ро | Т То | <7 |
а | ? |
Jo | ф(Х) |
ат | ъ |
м |
| 2,00 |
0,0214 | 0,0641 |
0,3333 | 0,2023 |
0,6324 | 0,8165 |
0,1497 | 2,500 |
18°26' | 52° 46' |
3,162 |
| 2,02 |
0,0185 | 0,0579 |
0,3199 | 0,1845 |
0,6196 | 0,8247 |
0,1378 | 2,515 |
17°51' | 54°31' |
3,260 |
| 2,04 |
0,0159 | 0,0520 |
0,3064 | 0,1672 |
0,6064 | 0,8328 |
0,1261 | 2,530 |
17° 18' | 56° 17' |
3,364 |
| 2,06 |
0,0136 | 0,0464 |
0,2927 | 0,1506 |
0,5927 | 0,8410 |
0,1148 | 2,545 |
16°44' | 58° 08' |
3,476 |
| 2,08 |
0,0115 | 0,0411 |
0,2789 | 0,1348 |
0,5785 | 0,8492 |
0,1037 | 2,561 |
16°09' | 60°02' |
3,595 |
| 2,10 |
0,0096 | 0,0361 |
0,2650 | 0,1198 |
0,5639 | 0,8573 |
0,0930 | 2,576 |
15°35' | 61°53' |
3,724 |
| 2,12 |
0,0079 | 0,0315 |
0,2509 | 0,1055 |
0,5487 | 0,8655 |
0,0827 | 2,592 |
15°00' | 63°57' |
3,863 |
| 2,14 |
0,0065 | 0,0273 |
0,2367 | 0,0920 • |
0,5330 | 0,8736 |
0,0728 | 2,607 |
14°26' | 65°59' |
4,105 |
| 2,16 |
0,0052 | 0,0233 |
0,2224 | 0,0795 |
0,5166 | 0,8818 |
0,0635 | 2,623 |
13°51' | 68°07' |
4,181 |
| 2,18 |
0,0041 | 0,0197 |
0,2079 | 0,0678 |
0,4995 | 0,8900 |
0,0546 | 2,639 |
13° 15' | 70° 18' |
4,364 |
| 2,20 |
0,0032 | 0,0164 |
0,1933 | 0,0570 |
0,4816 | 0,8991 |
0,0464 | 2,654 |
12°39' | 72°35' |
4,654 |
| 2,22 |
0,0024 | 0,0135 |
0,1786 | 0,0472 |
0,4629 | 0,9063 |
0,0387 | 2,670 |
12°02' | 74°57' |
4,796 |
| 2,24 | 0,0018 | 0,0108 | 0,1637 | 0,0383 | 0,4432 | 0,9145 | 0,0318 | 2,686 |
11 °25' | 77°25' |
5,054 |
| 2,26 |
0,0013 | 0,0085 |
0,1487 | 0,0304 |
0,4224 | 0,9226 |
0,0254 | 2,702 |
11 °47' | 80°0Г |
5,350 |
| 2,28 |
0,0009 | 0,0065 |
0,1336 | 0,0235 |
0,4004 | 0,9308 |
0,0198 | 2,719 |
11°07' | 82°36' |
5,695 |
| 2,30 |
0,0006 | 0,0048 |
0,1183 | 0,0175 |
0,3768 | 0,9390 |
0,0149 | 2,735 |
10°26' | 85°42' |
6,104 |
| 2,32 |
0,0004 | 0,0034 |
0,1029 | 0,0124 |
0,3514 | 0,9470 |
0,0107 | 2,751 |
9°43' | 88°46' |
6,601 |
| 2,34 |
0,0002 | 0,0023 |
0,0874 | 0,0083 |
0,3238 | 0,9553 |
0,0072 | 2,767 |
8° 57' | 92° 08' |
7,226 |
| 2,36 |
0,0001 | 0,0014 |
0,0717 | 0,0051 |
0,2933 | 0,9635 |
0,0045 | 2,784 |
8° 08' | 95°48' |
8,095 |
| 2,38 |
0,00004 | 0,0009 |
0,0559 | 0,0029 |
0,2590 | 0,9716 |
0,0025 | 2,800 |
7° 17' | 99°54' |
9,188 |
| 2,40 |
0,00001 | 0,00032 |
0,0400 | 0,0012 |
0,2190 | 0,9798 |
0,0011 | 2,817 |
6°14' | 104°42' |
10,96 |
| 2,42 |
0,000002 | 0,00009 |
0,0239 | 0,00032 |
0,1694 | 0,9880 |
0,0003 | 2,833 |
4°01' | 110°32' |
14,29 |
| 2,44 |
0 | 0,000005 |
0,00077 | 0,00005 |
0,0962 | 0,9961 |
0,00002 | 2,850 |
2°15' | 119°08' |
25,37 |
| 2,4495 |
0 | 0 | 0 |
0 | 0 | 1,0 |
0 | 2,858 | 0 | 130°21' | оо |
ГАЗОДИНАМИЧЕСКИЕ ФУНКЦИИ ДЛЯ *=1,3
| X |
р Ро | Р Ро | Т То |
я | а ~а7 | 5 | 1о |
“т | ь |
м |
| 0,02 |
0,9998 | 0,9998 |
0,9999 | 0,03187 |
1,072 | 0,00722 |
0,00023 |
0,01865 | ||
| 0,04 |
0,9991 | 0,9993 |
0,9998 | 0,06369 |
1,072 | 0,0144 |
0,00090 | _ |
0,03730 | |
| 0,06 |
0,9980 | 0,9985 |
0,9995 | 0,09546 |
1,072 | 0,0217 |
0,00203 | _ |
0,05506 | |
| 0,08 |
0,9964 | 0,9972 |
0,9992 | 0,1271 |
1,072 | 0,0289 |
0,00361 | _ | _ | 0,07463 |
| 0,10 | 0,9944 | 0,9957 | 0,9987 | 0,1581 | 1,072 | 0,0361 |
0,00563 | _ | 0,09331 | |
| 0,12 |
0,9919 | 0,9937 |
0,9981 | 0,1900 |
1,071 | 0,0433 |
0,00809 | _ | _ | 0,11200 |
| 0,14 | 0,9890 | 0,9915- | 0,9974 | 0,2212 |
1,071 | 0,0506 |
0,01098 |
0,1307 | ||
| 0,16 |
0,9855 | 0,9888 |
0,9967 | 0,2521 |
1,071 | 0,0578 |
0,01431 | _ | _ | 0,1494 |
|
0,18 | 0,9818 |
0,9860 | 0,9958 |
0,2828 | 1,070 |
0,0651 | 0,01806 |
_. | _ | 0,1682 |
| 0,20 | 0,9776 | 0,9827 | 0,9948 | 0,3179 | 1,070 |
0,0722 | 0,02222 |
_ | _ |
0,18701 |
| 0,22 | 0,9729 | 0,9791 | 0,9937 | 0,3432 | 1,069 | 0,0795 |
0,02679 | _ |
_ | 0,2058 |
|
0,24 | 0,9679 |
0,9752 | 0,9925 |
0,3729 | 1,068 |
0,0867 | 0,03175 |
_ | _ | 0,2246 |
| 0,26* | 0,9623 | 0,9709 | 0,9912 | 0,4022 | 1,068 |
0,093 | 0,03710 |
0,2435 | ||
|
0,28 | 0,9564 |
0,9663 | 0,9898 |
0,4311 | 1,067 |
0,1011 | 0,04282 |
_ | 0,2624 | |
|
0,30 | 0,9501 |
0,9614 | 0,9883 |
0,4596 | 1,066 |
0,1083 | 0,04891 |
_ | _. | 0,2814 |
| 0,32 |
0,9434 | 0,9562 |
0,9866 | 0,4875 |
1,065 | 0,1156 |
0,05543 | _ | __ | 0,3004 |
|
0,34 | 0,9363 |
0,9506 | 0,9849 |
0,5150 | 1,064 |
0,1279 | 0,06211 |
_ | _ | 0,3195 |
| 0,36 | 0,9288 | 0,9448 | 0,9831 | 0,5420 | 1,063 |
0,1300 | 0,06921 |
_ | — |
0,3386 |
| 0,38 |
0,9209 | 0,9386 |
0,9812 | 0,5683 |
1 ,062 | 0,1372 |
0,07660 | _ „ | _ | 0,3577 |
|
0,40 | 0,9127 |
0,9321 | 0,9791 |
0,5491 | 1,061 |
0,1444 | 0,08430 |
_ | _ | 0,3769 |
| 0,42 | 0,9040 | 0,9253 | 0,9770 | 0,6193 | 1,060 |
0,1517 | 0,09226 |
_ | 0,3962 | |
| 0,44 | 0,8951 |
0,9183 | 0,9747 |
0,6438 • | 1,059 |
0,1589 | 0,1005 |
_ | _ | 0,4156 |
| 0,46 |
0,8851 | 0,9109 |
0,9724 | 0,6677 |
1 ,057 | 0,1661 |
0,1089 | _ | _ |
0,4340 |
| 0.48 | 0,8761 | 0,9033 | 0,9699 | 0,6909 | 1,056 | 0,1733 |
0,1176 | _ |
_ | 0,4545 |
|
0,50 | 0,8662 |
0,8954 | 0,9674 |
0,7133 | 1,055 |
0,1806 | 0,1265 | 0,4740 | ||
|
0,52 | 0,8559 |
0,8872 | 0,9647 |
0,7531 | 1,053 |
0,1878 | 0,1356 |
_ | о’4937 | |
| 0,54 | 0,8453 |
0,8788 | 0,9620 |
0,7561 | 1,052 |
0,1950 | 0,1448 |
“ | | — | 0,5134 |
|
X | р Pi, |
Р Ро | Т То | Q |
а а, |
/о | ат |
5 | м | |
| 0,56 | 0,8344 |
0,8700 | 0,9591 |
0,7763 ‘ | 1,050 |
0,2022 | 0,1542 | 0,5332 | ||
|
0,58 | 0,8233 |
0,8610 | 0,9561 |
0,7958 | 1,049 |
0,2095 | 0,1637 |
— | _ |
0,5531 |
| 0,60 |
0,8119 | 0,8519 |
0,9530 | 0,8145 |
1,047 | 0,2167 |
0,1733 | — |
_ | 0,5731 |
| 0,62 | 0,8002 |
0,8424 | 0,9499 |
0,8322 | 1,045 |
0,2239 | 0,1830 |
— | _ |
0,5932 |
| 0,64 |
0,7883 | 0,8328 |
0,9466 | 0,8493 |
1,043 | 0,2311 |
0,1928 | — |
— | 0,6134 |
| 0,66 | 0,7760 |
0,8229 | 0,9432 |
0,8653 | 1,041 |
0,2384 | 0,2026 |
— | — |
0,6337 |
| 0,68 |
0,7637 | 0,8127 |
0,9397 | 0,8806 |
1,039 | 0,2456 |
0,2124 | — |
_ | 0,6541 |
| 0,70 | 0,7511 |
0,8024 | 0,9361 |
0,8950 | 1,038 |
0,2528 | 0,2222 |
— | — |
0,6747 |
| 0,72 |
0,7384 | 0,7919 |
0,9324 | 0,9085 |
1,035 | 0,2600 |
0,2320 | — |
_ | 0,6953 |
| 0,74 | 0,7253 |
0,7811 | 0,9286 |
0,9211 | 1,033 |
0,2672 | 0,2418 |
— | — |
0,7161 |
| 0,76 |
0,7122 | 0,7702 |
0,9247 | 0,9327 |
1,031 | 0,2745 |
0,2514 | _ |
— | 0,7570 |
| 0,78 | 0,6989 |
0,7591 | 0,9206 |
0,9435 | 1,029 |
0,2817 | 0,2610 |
— | — |
0,7580 |
| 0,80 |
0,6854 | 0,7478 |
0,9165 | 0,9533 |
1 ,027 | 0,2889 |
0,2705 | — |
— | 0,7792 |
| 0,82 | 0,6718 |
0,7364 | 0,9123 |
0,9622 | 1,024 |
0,2961 | 0,2799 |
— | — |
0,8806 |
| 0,84 |
0,6581 | 0,7248 |
0,9080 | 0,9702 |
1,022 | 0,3034 |
0,2891 | — |
— | 0,8220 |
| 0,86 | 0,6443 |
0,7130 | 0,9053 |
0,9771 | 1.019 |
0,3106 | 0,2981 |
— | — |
0,8437 |
| 0,88 |
0,6304 | 0,7012 |
0,8990 | 0,9833 |
1,017 | 0,3178 |
0,3070 | — |
— | 0,8655 |
| 0,90 | 0,6164 |
0,6892 | 0,8943 |
0,9884 | 1,014 |
0,3250 | 0,3155 |
— | — | 0,8874 |
| 0,92 |
0,6023 | 0,6771 |
0,8896 | 0,9925 |
1,011 | 0,3323 |
0,3239 | — |
— | 0,9096 |
| 0,94 | 0,5882 |
0,6649 | 0,8847 |
0,9958 | 1,009 |
0,3395 | 0,3320 |
— | — |
0,9319 |
| 0,96 |
0,5740 | 0,6525 |
0,8798 | 0,9982 |
1,006 | 0,3467 |
0,3399 | — |
— | 0,9544 |
| 0,98 | 0,5599 |
0,6401 | 0,8747 |
0,9996 | 1,003 |
0,3539 | 0,3475 |
— | — |
0,9771 |
| 1,00 |
0,5457 | 0,6276 |
0,8696 | 1,0000 |
1,000 | 0,3612 |
0,3547 | 90° |
0 | 1,0000. |
| 1,02 | 0,5315 |
0,6150 | 0,8643 |
0,9995 | 0,9970 |
0,3684 | 0,3616 |
77°47' | 0°10' |
1,0231 |
| 1,04 | 0,5174 | 0,6024 | 0,8589 | 0,9982 | 0,9939 | 0,3756 | 0,3683 | 72° 52' | 0°30' | 1,046 |
| 1 ,06 | 0,5032 | 0,5897 | 0,8534 | 0,9960 | 0,9997 | 0,3828 | 0,3745 | 69°09' | 0°55' | 1,069 |
|
1,08 | 0,4891 |
0,5769 | 0,8479 |
0,9928 | 0,9874 |
0,3900 | 0,3803 |
66° 06' | Г25' |
1,094 |
| 1,10 |
0,4750 | 0,5641 |
0,8422 | 0,9887 |
0,9841 | 0,3973 |
0,3858 | 63°26' |
Г55' | 1,118" |
| 1,12 | 0,4611 |
0,5513 | 0,8364 |
0,9838 | 0,9307 |
0,4045 | 0,3909 |
61 °07' | 2°25' |
1,142 |
| 1,14 |
0,4471 | 0,5384 |
0,8305 | 0,9780 |
0,9773 | 0,4117 |
0,3955 | 59°00' |
2°5' | 1,163 |
| 1,16 | 0,4333 |
0,5268 | 0,8245 |
0,9737 | 0,9737 |
0,4189 | 0,4406 |
57°05' | 3°28' |
1,191 |
| 1,18 |
0,4196 | 0,5127 |
0,8184 | 0,9640 |
0,9701 | 0,4262 |
0,4035 | 55° 18' |
4°19' | 1,216. |
| 1,20 | 0,4050 |
0,4998 | 0,8122 |
0,9558 | 0,9664 |
0,4334 | 0,4068 |
53°38' | 4°52' |
1,242 |
| 1,22 |
0,3925 | 0,4870 |
0,8059 | 0,9467 |
0,9627 | 0,4406 |
0,4097 | 52°06' |
5°37' | 1,267 |
| 1,24 | 0,3791 |
0,4742 | 0,7994 |
0,9370 | 0,9588 |
0,4478 | 0,4121 |
50°38' | 6°20' |
1,293 |
| 1,26 | 0,3659 | 0,4614 | 0,7929 | 0,9264 | 0,9549 | 0,4551 | 0,4140 | 49° 16' | 7° 08' | 1,319' |
| 1,28 |
0,3528 | 0,4487 |
0,7863 | 0,9152 |
0,9509 | 0,4623 |
0,4155 | 47°59' |
7°52' | 1,346 |
| 1,30 | 0,3399 |
0,4360 | 0,7796 |
0,9032 | 0,9468 |
0,4695 | 0,4165 |
46°45' | 8°44' |
1 ,373 |
| 1,32 |
0,3272 | 0,4234 |
0,7727 | 0,8908 |
0,9427 | 0,4767 |
0,4170 | 45°35' |
9°32' | 1,400 |
| 1,34 | 0,3147 |
0,4109 | 0,7658 |
0,8773 | 0,9384 |
0,4839 | 0,4170 |
44°27' | 10°16' |
1 ,428 |
| 1,36 |
0,3023 | 0,3984 |
0,7588 | 0,8634 |
0,9341 | 0,4912 |
0,4165 | 43°23' |
11 ° 18' | 1,456 |
| 1,38 | 0,2901 |
0,3960 | 0,7516 |
0,8489 | 0,9297 |
0,4984 | 0.4155 |
42°28' | 12°01' |
1,484 |
| 1,40 | 0,2782 | 0,3738 | 0,7444 | 0,8338 | 0,9252 | 0,5056 | 0,4141 | 4 Г 24' | 13° 17' | 1,513 |
| 1,42 |
0,2665 | 0,3616 |
0,7370 | 0,8182 |
0,9206 | 0,5128 |
0,4121 | 40°20' |
14°04' | 1,542 |
| 1,44 | 0,2550 |
0,3495 | 0,7295 |
0,8020 | 0,9159 |
0,5201 | 0,4097 |
39°30' | 14°52' |
1 ,572' |
| 1,46 |
0,2438 | 0,3376 |
0,7220 | 0,7854 |
0,9112 | 0,5273 |
0,4068 | 38°37' |
15°59' | 1,602 |
| 1,48 | 0,2327 |
0,3258 | 0,7143 |
0,7683 | 0,9063 |
0,5345 | 0,4034 |
37°46' | 16°59' |
1,633 |
| 1,50 |
0,2219 | 0,3142 |
0,7065 | 0,7510 |
0,9014 | 0,5417 |
0,3996 | 36°56' |
18°00' | 1,664- |
| 1,52 | 0,2114 |
0,3026 | 0,6986 |
0,7329 | 0,8963 |
0,5490 | 0,3952 |
36°08' | 18°54' |
1 ,696- |
| 1 ,54 |
0,2011 | 0,2912 |
0,6907 | 0,7146 |
0,8912 | 0,5562 |
0,3904 | 35°38' |
20°05' • | 1,728- |
| 1,56 | 0,1911 |
0,2800 | 0,6826 |
0,6961 | 0,8860 |
0,5634 | 0,3852 |
34° 39' | 21 °06' |
1 ,761 |
| 1,58 |
0,1814 | 0,2690 |
0,6744 | 0,6772 |
0,8806 | 0,5706 |
0,3795 | 33°53' |
22°08' | 1 ,794 |
| 1,60 | 0,1719 |
0,2581 | 0,6661 |
0,6580 | 0,8752 |
0,5778 | 0,3735 |
33°10' | 23° 15' |
1 ,828 |
| 1,62 |
0,1627 | 0,2474 |
0,6577 | 0,6387 |
0,8692 | 0,5851 |
0,3670 | 32° 28' |
24°2Г | 1,863 |
| 1,64 | 0,1538 |
0,2369 | 0,6492 |
0,6191 | 0,8640 |
0,5923 | 0,3602 |
31 °47' | 25° 29' |
1 ,898 |
| 1,66 |
0,1452 | 0,2266 |
0,6406 | 0,5994 |
0,8583 | 0,5995 |
0,3529 | 31 °08' |
26°38' | 1,934 |
| 1,68 | 0,1368 |
0,2165 | 0,6319 |
0,5795 | 0,8524 |
0,6067 | 0,3454 |
30°30' | 27047' |
1,971 |
| 1,70 |
0,1287 | 0,2066 |
0,6231 | 0,5596 |
0,8465 | 0,6140 |
0,3375 | 29°52' |
28°55' | 2,008 |
| 1,72 | 0,1209 |
0,1969 | 0,6141 |
0,5396 | 0,8404 |
0,6212 | 0,3292 |
29° 15' | 30°07' |
2,047 |
| X | Р Ро | р Ро | т То | я |
а а# | $ | Jo | “m |
г | м |
|
1,74 1,76 1,78 1,80 1,82 1,84 |
0,1134 0,1062 0,09922 0,09256 0,08718 0,08007 |
0,1874 0,1781 0,1691 0,1603 0,1517 0,1434 |
0,6051 0,5960 0,5867 0,5774 0,5680 0,5584 |
0,5196 0,4996 0,4796 0,4598 0,4400 0,4204 |
0,8342 0,8279 0,8214 0,8149 0,8082 0,8014 |
0,6284 0,6356 0,6429 0,6501 0,6573 0,6645 |
0,3207 0,3119 0,3028 0,2936 0,2841 0,2744 |
28°37' 28°03' 27°29' 26°55' 26°22' 85°49' |
31°13' 32°27' 33°45' 35°04' 36°24' 37°33' |
2,086 2,126 2,167 2,209 2,252 2,296 |
| 1,86 1,88 1,90 1,92 1,94 1,96 |
0,07424 0,06870 0,06341 0,05840 0,05364 0,04915 |
0,1353 0,1274 0,1198 0,1125 0,1054 0,09851 |
0,5488 0,6390 0,5291 0,5192 0,5091 0,4989 |
0,4010 0,3818 0,3628 0,3441 0,3257 0,3077 |
0,7944 0,7873 0,7801 0,7727 0,7652 0,7575 |
0,6717 0,6790 0,6862 0,6934 0,7006 0,7079 |
0,2645 0,2545 0,2445 0,2344 0,2241 0,2139 |
25° 17' 24°49' 24°14' 23°44' 23°18' 22°44' |
38°53' 40°22' 41°33' 43°06' 44° 14' 45° 36' | 2,341 2,388 2,436 2,485 2,535 2,587 |
| 1,98 2,00 2,02 2,04 2,06 2,08 |
0,04491 0,04092 0,03717 0,03366 0,03038 0,02732 |
0,09191 0.08556 0,07946 0,07363 0,06804 0,06271 |
0,4887 0,4783 0,4678 0,4572 0,4465 0,4357 |
0,2900 0,2727 0,2595 0,2393 0,2233 0,2078 |
0,7496 0,7416 0,7334 0,7251 0,7166 0,7079 |
0,7151 0,7223 0,7295 0,7368 0,7440 0,7512 |
0,2037 0,1934 0,1833 0,1732 0,1632 0,1533 |
22° 19' 2Г46' 21°17' 20°49' 20°21' 19°54' | 47°04' 48°25' 49°52' 41°14' 52°45' 54° 19' | 2,641 2,697 2,754 2,813 2,875 2,938 |
| 2,10 2,12 2,14 2,16 2,18 2,20 | 0,02448 0,02185 0,01942 0,01718 0,01513 0,01325 | 0,04762 0,05280 0,04822 0,04389 0,03979 0,03595 |
0,4248 0,4138 0,4027 0,3915 0,3801 0,3687 |
0,1928 0,1784 0,1644 0,1511 0,1382 0.1260 |
0,6989 0,6898 0,6805 0,6710 0,6612 0,6512 |
0,7584 0,7656 0,7729 0,7801 0,7873 0,7945 |
0,1430 0,1341 0,1248 0,1157 0,1069 0,09835 |
19°26' 18°59' 18°32' 18°06' 17°39' 17° 13' |
55° 53' 57°24' 58°52' 60°30' 62° 15' 64°22' | 3,004 3,073 3,145 3,219 3,297 3,378 |
662
I б°47'
16°21' 15°55' 15°29' 15°03 14°37'
14° 11'
13°45' 13° 19'
12°52' 12°26' 11°59'
II °32' 11 °05' 10°37' 10°09'
9°40' 9°11'
8°41' 8°09' 7°36' 7° 02' 6°25' 5°46'
5° 03' 4° 14' 3°13' 1 °46' 0
3,464
3,553
3,647
3,747
3,852
3,963
4,081
4,208
4,342
4,487
4,644
4,813
4,998
5,2000
5,423
5,671
5,949
6,264
6,627
7,049
7,551
8,162
8,931
9,941
11,35
13,55
17,72
32,07
оо
66°00' 67 °21' 68°08' 71 °06' 72°44' 74°36'
76°30'
78°29'
80°31'
82°52'
84°ЗГ
86°51'
89°04' 91 °24' 93°48' 96°22' 98°54' 101 °37'
104°27' 107°26' 110°37' 114°21' 117°37' 121 °41'
126°08' 131 °25' 137°47' 147° 19' 159° 12'
0,09008
0,08210
0,07448
0,06723
0,06031
0,05376
0,04760
0,04184
0,03647
0,3152
0,02694
0,02278
0,01905
0,01568
0,1272
0,01008
0,00788
0,00596
0,00440
0,00310
0,00210
0,00134
0,00080
0,00041
0,00020
0,00004
0,00001
О
0
0,8018
0,8090
0,8162
0,8234
0,8307
0,8379
0,8451
0,8523
0,8596
0,8668
0,8740
0,8812
0,8884
0,8957
0,9029
0,9101
0,9173
0,9246
0,9318
0,9390
0,9462
0,9535
0,9607
0,9679
0,9751
0,9823
0,9896
0,9968
1,0
0,6409
0,6304
0,6196
0,6085
0,5971
0,5854
0,5733
0,5609
0,5481
0,5348
0,5211
0,5069
0,4922
0,4769
0,4610
0,4444
0,4270
0,4086
0,3893
0,3688
0,3740
0,3234
0,2978
0,2698
0,2378
0,2007
0,1546
0,08606
0,00679
о
о
со
| 2,22 | 0,01155 |
0,03234 | 0,3572 |
0,1144 |
| 2,24 |
0,01050 | 0,02895 |
0,3455 | 0,1033 |
| 2,26 | 0,00861 |
0,02580 | 0,3338 |
0,09291 |
| 2,28 | 0,00770 | 0,02288 | 0,3220 | 0,08313 |
| 2,30 |
0,00625 | 0,02017 |
0,3100 | 0,07392 |
| 2,32 | 0,00527 |
0,01767 | 0,2980 |
0,06531 |
| 2,34 , | 0,00440 | 0,01538 | 0,2858 | 0,05735 |
| 2,36 |
0,00364 | 0,01329 |
0,2736 | 0,04997 |
| 2,38 | 0,00298 |
0,01139 | 0,2612 |
0,04320 |
| 2,40 | 0,00241 | 0,00968 | 0,2487 | 0,03702 |
| 2,42 |
0,00192 | 0,00814 |
0,2361 | 0,03139 |
| 2,44 | 0,00151 |
0,00677 | 0,2235 |
0,02632 |
| 2,46 | 0,00117 | 0,00557 | 0,2107 | 0,02183 |
| 2,48 |
0,00089 | 0,00451 |
0,1978 | 0,01781 |
| 2,50 . | 0,00066 |
0,00360 | 0,1848 |
0,01434 |
| 2,52 | 0,00048 | 0,00281 | 0,1717 | 0,01128 |
| 2,54 |
0,00034 | 0,00216 |
0,1585 | 0,00875 |
| 2,56 | 0,00024 |
0,00161 | 0,1452 |
0,00656 |
| 2,58 | 0,00015 | 0,00117 | 0,1318 | 0,00481 |
| 2,60 | 0,00010 | 0,00081 | 0,1183 | 0,00336 |
|
2,62 | 0,00006 |
0,00054 | 0,1047 |
0,00225 |
| 2,64 |
0,00003 | 0,00034 |
0,09096 | 0,00143 |
| 2,66 | 0,00002 |
0,00020 | 0,07713 |
0,00084 |
| 2,68 |
0,000006 | 0,00010 |
0,06320 | 0,00043 |
| 2,70 | 0,000002 |
0,00005 | 0,04917 |
0,00022 |
| 2,72 |
0 | 0,00001 | 0,03503 | 0,00005 |
|
2,74 | 0 | 0,000002 | 0,02078 | 0,000008 |
| 2,76 | 0 |
0 | 0,00644 |
0 |
| 2,76887 |
0 | 0 | 0,00004 | 0 |
ЛИТЕРАТУРА
1. Н. Е. Жуковский, Видоизменение метода Кирхгофа, Полное собрание сочинений, т. III, ОНТИ, 1936.
2. Н. Е. Жуковский, О присоединенных вихрях, Полное собрание сочинений, т. V, ОНТИ, 1936.
3. Н. Е. Жуковский, Вихревая теория гребного винта, Полное собрание сочинений, т. VI, ОНТИ, 1936.
4. С. А. Чаплыгин, Теория решетчатого крыла, Собрание сочинений, т. II, Гидродинамика, Аэродинамика, Гостехиздат, 1948.
5. С. А. Чаплыгин, О газовых струях, Собрание сочинений, т, II, ГИТТЛ, 1948.
6. Л. Г. Л о й ц я н с к и й, Механика жидкости и газа, Гостехиздат, 1957.
7. Л. И. Седов, Плоские задачи гидродинамики и аэродинамики, Гостехиздат, 1954.
8. Н. С. Аржаников и В. Н. Мальцев, Аэродинамика, Оборонгиз, 1957.
9. Г. Н. Абрамович, Прикладная газовая динамика, Гостехиздат, 1953.
10. Л. И. Седов, Методы подобия и размерности в механике, Гостехиздат, 1950.
11. В. С. Жуковский, Техническая термодинамика, Гостехиздат, 1952.
12. Л. А. В у л и с, Термодинамика газовых потоков, Госэнер-гоиздат, 1950.
13. Л. Прандтль, Гидроаэромеханика, Изд. иностранной литературы, 1949.
14. Современное состояние гидроаэродинамики вязкой жидкости, Сборник под редакцией С. Гольдштейна, Изд. иностранной литературы, 1948.
15. Современное состояние аэродинамики больших скоростей, Сборник под редакцией Р. Хоуэрта, Изд. иностранной литературы,
16. Н. Е. К о ч и н, Гидродинамическая теория решеток, ГИТТЛ,
1949.
17. Т. Карман, Сверхзвуковая аэродинамика, Изд. иностранной литературы, 1948.
К гл. 1
1. Н. Я- Фабрикант, Аэродинамика, Гостехиздат, 1955.
2. А. П. Мельников, Основы теоретической аэродинамики, Изд. ЛКВВИА, 1953.
К гл. 2
1. Ф. И. Ф р а н к л ь, С. А. Христланович, Р. Н. Алексеева, Основы газовой динамики, Труды ЦАГИ, вып. 364, 1938.
2. С. А. Хр и с т и а н о в и ч, В. Г. Гальперин, М. Д. Миллионщиков, Л. А. Симонов, Прикладная газовая динамика, Изд. ЦАГИ, 1948.
3. Б. М. Киселев, Расчет одномерных газовых течений, «Прикладная математика и механика», 1947, № 1.
К гл. 3
1. С. А.-X р и с т и а н о в и ч, Обтекание тел газом при больших дозвуковых скоростях, Труды ЦАГИ, вып. 481, 1940.
2. С. А. Христианович, О сверхзвуковых течениях газа, Труды ЦАГИ, вып. 543, 1941.
3. А. Н. Шерстюк, Расчет крыловых профилей при больщих дозвуковых скоростях, Известия АН СССР, ОТН, 1956, № 8.
4. Г. Ф. Б у р а г о, Теория крыловых профилей с учетом влияния сжимаемости воздуха, Изд. ВВИА им. Н Е. Жуковского, 1949,
5. Л. И. С е д о в, Плоские задачи гидродинамики и аэродинамики, Гостехиздат, 1950.
6. Н. Я. Фабрикант, Аэродинамика, Гостехиздат, 1949.
7. Г. Ф. Б у р а г о, Б. Я- Ш у м я ц к и й, Основы теоретической аэрогидромеханики, ч. I, Изд. ВВИА им. Н. Е. Жуковского, 1951.
8. В. С. П о л я д с к и й, Расчет распределения давления при больших скоростях полета, Изд. Бюро новой техники, 1943.
9. Г. В. Л и п м а н, А. Е. Пакет, Введение в аэродинамику сжимаемой жидкости, Изд. иностранной литературы, 1949.
10. Проблемы полета с большими скоростями, Сборник статей, Изд. иностранной литературы, 1960.
К гл. 4
1. Я. И. Левинсон, Аэродинамика больших скоростей, Оборонгиз, 1950.
2. А. Ферри, Аэродинамика сверхзвуковых скоростей, Гостехиздат, 1952.
3. Р. Зауэр, Течения сжимаемой жидкости, Изд. иностранной литературы, 1954.
4. В. А. Андреев, С. 3. Беленький, Влияние конденсации паров воды на сверхзвуковые течения, труды ЦАГИ, № 579, БНТ, 1946.
5. F. W. R о s s, The propagation in a compressible fluid of finite oblique distrurbances with energy exchange and change of state, Journal of Applied Physics, 1951, v. 22, № 12.
К гл. 5
1. Г. М. Бам-Зеликович, Расчет отрыва пограничного слоя, Известия АН СССР, ОТН, 1954, № 12.
2. А. А. Г у х м а н, А. Ф. Г а н д е л ь с м а н, Н. В. Илюхин, Исследование изменения коэффициента сопротивления при течении газа со сверхзвуковой скоростью, «Теплоэнергетика», 1955, № 1.
3. А. А. Г у х м а н, А. Ф. Г андельсм ан, Л. Н. Н а у р и ц, О гидродинамическом сопротивлении в трансзвуковой области течения ^Теплоэнергетика», 1957, № 7.
4. М. Е. Дейч, А. Е. Зарянки н, Экспериментальное исследование турбулентного пограничного слоя при больших дозвуковых скоростях, «Теплоэнергетика», 1958, № 3.
5. М. Е. Дейч, А. Е. 3 а р я н к и н, Приближенный метод расчета турбулентного пограничного слоя при больших скоростях, Труды МЭИ,, вып. XXX, 1958.
6. А. А. Дородницын, Пограничный слой в сжимаемом газе, «Прикладная математика и механика», 1942, т. VI, № 6.
7.'А. Е. 3 а р я н к и н,'Исследование пограничного слоя в турбинных решетках при больших скоростях, Диссертация, МЭИ, 1956.
8. Л. М. Зысина-Моложен, О характере перехода" от ламинарного к турбулентному режиму течения в пограничном слое, Журнал технической физики, 1955, т. XXV, вып. 7.
9. Л. Е. К а л и х м а н, Газодинамическая теория теплопередачи, «Прикладная математика и механика», 1956, т. X.
'10. Л. Е. К а л и х м а н, Турбулентный пограничный слой на плоской пластинке, обтекаемой газом, Оборонгиз, 1954.
11. Л. Г. Л о йц я некий, Аэродинамика пограничного слоя, Гостехиздат, 1941.
12. Е. М. Минский, Влияние турбулентности набегающего потока на переход, Труды ЦАГИ, вып. 415, 1939.
13. А. П. Мельников, Основы теоретической аэродинамики, Изд. ЛКВВИА, 1953.
14. Б. С. Петухов, А. С. С у к о м е л, В. С. Протопопов, Исследование сопротивления трения и коэффициента восстановления температуры стенки при движении газа в круглой трубе с высокой дозвуковой скоростью, «Теплоэнергетика», 1957, № 3.
15. Г. Ш л и х т и н г, Теория пограничного слоя, Изд. иностранной литературы, 1956.
16. Н. N i р р е г t, Ober den Strommungsverlust in gekriimmten Kanalen, Forschungsarbeiten auf d. Geb. У. Ing. Wes, 1929, H. 320
17. J. P. Hartnett, E. R. Eckert., Experimental study of the velocity and temperature distribution in a high-velocity vortex-type flow, Transaction of the ASME, 1957, v. 79, № 4.
18. А. П. Алексеев, В. С. Мартыновский, Исследование эффекта вихревого- температурного разделения газов н паров, Известия АН СССР, ОТН, 1956, т. 26, № 10.
19. Л. А. Вули с, Об эффекте Ранка, Известия АН СССР,
ОТН, 1956, № 10.
20. М. Г. Д у б и н с к и й, О вращающихся потоках газа, Известия АН СССР, ОТН, 1954, № 8.
К гл. 6
1. В. И. Астров, Е. А. Левин, Л. Д. Павлов, С. А. X р и-
стианович, О расчете сопел Лаваля, «Прикладная математика
п механика», вып. 1, т. II, 1943.
2. А. В. Болгарский, В. К- Щукин, Рабочие процессы в жидкостно-реактивных двигателях, Оборонгиз, 1958.
3. Н. Д. Доброхотов, Газодинамические схемы истечения из сопла ракетного двигателя при нерасчетном давлении, 1947.
4. М. С. К и с е н к о, Сравнительные испытания нескольких вариантов сопел, Труды ЦАГИ, вып. 478, 1940.
5. J. Е. В е с k w i t h., J. A. M о о t e 1., An accurate and rapid method {or the design of supersonic nozzles, NACA, TN, 1956, № 3322.
6. A. S t о d о 1 a, Dampf-und Gasturbinen, 1924.
1. Аэродинамика, Под общей редакцией В. Ф. Дюренда, т. П1, Оборонгиз, 1940.
2. Л. П. Волкова, М. Я- Юделович, Потери на удар в ступенчатых трубках при сверхзвуковых отношениях давления, Изв. АН СССР, ОТН, 1958, № 4.
3. И. Д. Винник, М. П. Уманский, В. А. Черников, Некоторые результаты аэрдинамического исследования выхлопного патрубка транопортного газотурбинного двигателя, «Энергомашиностроение», № 4, 1959.
4. А. Ш. Д о р ф м а н, М. М. Назарчук, Н. И, Польский, М. И. С а й к о в с к >к й, Аэродинамика диффузоров и выхлопных патрубков трубомашин, Изд. АН УССР, 1960.
5. М. Е. Дейч, А. В. Р о б о ж е в, Ф. В. Степан чу к,
А. А. Ко х, Исследование структуры потока в ступени эжектора с изобарическим начальным участком смешения, «Теплоэнергетика», 1954, № 12.
6. М. Е. Дейч, А. В. Р о б о ж е в, А. А. Ко х, Влияние некоторых геометрических и газодинамических параметров ступени эжектора на эффективность ее работы, Труды МЭИ, вып. XXIII, 1955.
7. М. А Дементьев, А. К. Чертков, Гидромеханическое исследование вариантов выхлопного патрубка паровой турбины, «Котлотурбостроение», 1948, № 1.
8. И. Е. И д е л ь ч и к, Гидравлические сопротивления, Госэнер-гоиздат, 1954.
9. О. Н. Овчинников, Влияние входного профиля скорости на работу диффузора, «Вестник машиностроения», 1954, № 6.
10. И. И. Орлов, Продувка моделей входного патрубка осевого компрессора, «Вестник машиностроения», 1954, № 6.
11. Р. Пэнкхерст, Д. Холле р, Техника эксперимента в аэродинамических трубах, Изд. иностранной литературы, 1955.
12. Е. Я. Соколов и Н. М. Зингер, Струйные аппараты, Госэнергоиздат, 1960.
13. Л. П. Соколовский, Исследование аэродинамики выходных патрубков турбин и компрессоров, «Энергомашиностроение»,
1952, № 9.
14. К. С. С ц и л л а р д, Исследование диффузоров аэродинамических труб больших скоростей, Технические заметки ЦАГИ, № 160, 1938.
15. Г. А. X а н и н, Некоторые вопросы аэродинамического исследования вспомогательных элементов проточной части турбомашин, «Теплоэнергетика», 1955, № 1.
16. Б. Н. Юрьев, Экспериментальная аэродинамика, Оборонгиз, 1939.
17. Ф. Клауз ер, Работа диффузоров прямоточных реактивных двигателей при сверхзвуковых скоростях полета, «Вопросы ракетной техники», 1954, № 2; 1955, We 1.
18. Е. Нейман, Ф. Люстверк, Сверхзвуковые диффузоры высокой эффективности, «Вопросы ракетной техники», 1951, № 6;
20. С. А. Хр нет иаяович, О расчете эжектора, «Промышленная аэродинамика», 1944, № 3.
21. С. А. Христ'ианович, М. Д. Миллионщиков, Г. М. Рябин ков, Ф. А. Т р е б н н, Применение эжекторов в газосборных сетях, Известия АН СССР, ОТН, 1946, № 3.
22 М. Н i b s, Mezikruhove difuzory, Proudeni v lopatkovych stro-jich, Sbornik lislavu pro vyzkum stroju, 1958.
23. V. К m о n i с e k, Zlepseni cinnosti difusoru jednoduchymi zasahy, Strojnicky sbornik, 1956, 13.
1. E. А. Г у к а с о в а, Исследование концевых потерь в решетках турбинных профилей, Труды ЦКТИ, Аэрогидродинамика, кн. 27, 1954.
2. М. Е. Дейч, К вопросу о концевых потерях в направляющих каналах паровых турбин, «Советское котлотурбостроение»,
1945, № 6.
3. М. Е. Дейч, А. В. Губарев, К вопросу о «запирании» подводящего сопла и рабочей решетки профилей в сверхзвуковом потоке, «Теплоэнергетика, 1960, № 12.
4. М. Е. Дейч, А. В. Губарев, Исследование активных рабочих решеток при больших скоростях», «Теплоэнергетика», 1958, № 12.
5. М. Е. Дейч, А. Е. Зарянкин, Г. А. Филиппов, М. Ф. Зацепин, Повышение эффективности турбинных активных решеток малой высоты, «Теплоэнергетика», 1960, № 9.
6. М. Е. Дейч, А. Е. Зарянкин, Приближенный метод расчета концевых потерь, «Теплоэнергетика», 1958, № 9.
7. М. Е. Дейч, Г. С. С а м о й л о в н ч, Основы аэродинамики осевых турбомашин, Машгиз, 1959.
8. М. Е. Дейч, В. В. Фролов, А. В. Губарев, Исследование новых профилей решеток регулирующих ступеней и ступеней давления турбин, «Теплоэнергетика», 1956, № 5.
9. М. Е. Дейч, К- А. Розанов, В. В. Фролов, Исследование и улучшение профилей двухвенечной регулирующей ступени, Труды МЭИ, вып. 23, 1955.
10. М. Е. Дейч, А. Е. 3 а р я н к н н, Исследование и улучшение сопловых решеток регулирующих ступеней, «Теплоэнергетика», 1955, № 10.
11. М. И .Жуковский, Расчет обтекания решеток профилей турбомашии, Машгиз, 1960.
12. М. И. Жуковский, Н. А. С к н а р ь, К вопросу о применении утолщенных кромок направляющих лопаток, «Энергомашиностроение», 1957, № 2.
13. М. И. Жуковский, Н. А. Скяарь, Новые решетки тур-б-инных профилей, «Теплоэнергетика», 1955, № 1.
14. В. И. Кирсанов, Об улучшении турбинных реактивных решеток профилей на основе исследования характера их обтекания при изменении режима работы по числу М и числу Re, Известия АН СССР ОТН, 1954, № 7.
15. Г. С. С а м о й л о в и ч, Расчет потенциального потока в криволинейном канале, «Теплоэнергетика», 1954, № 7-
16. Г. Ю. Степанов, Гидродинамические исследования турбинных решеток, «Обзорный бюллетень авиамоторостроения», 1949, № 4 и 5.
17. Г. Ю. Степанов, Основы теории лопаточных машин, комбинированных и газотурбинных двигателей, Машгиз, 1958.
18. Н. М. Марко в, Расчет аэродинамических характеристик лопаточного аппарата турбомашин, Машгиз, 1955.
19. И. Д. Л я х о в и ц к и й, Турбулентность потока в турбинной ступени и профильные потери активных лопаток, «Известия ВТИ»,
1950, № 5.
20. Н. Г. Родин, О концевых потерях энергии в решетках турбинных лопаток, Труды ЛПИ, 1951, № 1.
21. О. Н. Емин, Вторичное течение и потери при движении
жидкости на повороте, Труды МАИ, вып. 68, 1956.
22. А. Н. Шерстюк, К определению потерь в турбинных ре
шетках с утолщенными выходными кромками, «Теплоэнерретика», 1959, № 6.
23. А. Н. Шерстюк, Приближенный метод расчета криволинейных каналов, «Теплоэнергетика», 1955, № 8.
24. Г. Ф л юг ель, Паровые турбины, ГОНТИ, 1939.
25. Л. Б е л и к, Применение теоретических и эксперименталь
ных методов при проектировании турбинных решеток активного типа, «Теплоэнергетика», 1958, № 8.
26. Я- Буковский, Методы экспериментального исследования потока в решетках -профилей турбомашин при больших скоростях, «Теплоэнергетика», 1958, № 9.
27. A. D., Corter, Е. М. Cohen, Preliminary investigation into the three-dimensional flow through a cascade of aerofoils, ARC,
1946, № 2339.
28. H. B. Squire, K- G. W i n t e r, The secondary flow in a
cascade of aerofoils in a non-uniform stream, J. Aeron. Sc, 1951,
v. 18, № 4.
29. J. M. Stephenson, Secondary flow in cascades, J. Aeron. Sc., 1951, v. 18, № 18.
30. P. H. Алексеева, И. Д. Л я x о в и ц к и й, Ю. В. Р ж е з-ников, «Теплоэнергетика», 1956, № 6.
1. М. Е. Дейч, Экспериментальные исследования и основы аэродинамического расчета ступеней паровых и газовых турбин, Диссертация, 1956.
2. М. Е. Дейч, Г. С. С а м о й л о в и ч, Основы аэродинамики осевых гурбомашин, Машгиз, 1959.
3. М. Е. Дейч, Ф. В. К а з и н ц е в, Л. Е. Киселев,
В. Г. Филлипов а, Исследование переменного режима ступеней с длинными лопатками постоянного профиля, «Теплоэнергетика», 1959, № 6.
4. В. Е. Ершов, К .вопросу о движении газа через ступень осевой турбомашины, Сборник трудов лаборатории быстроходных машин и механизмов, вып. 5, 1955.
5. Г. С. Ж и р и ц к н й, Авиационные газовые турбины, Оборонгиз, 1950.
6. И. И. Кириллов, Метод проектирования проточной части паровых туобин с закрученными лопатками. Сборник трудов, БИТМ, вып. 15, 1955.
7. И. И. К Hip и л лов, Газовые турбины и газотурбинные установки, Машгиз, 1956.
8. Б. С. Стечкин, П. К. Казанджан, Л. П. Алексеев,
А. Н. Говоров, Ю. Н. Нечаев, Р. М. Федоров, Теория реактивных двигателей (лопаточные машины), Оборонгиз, 1956.
9. Г. С. Самойлович, Б. М. Трояновский, Переменный режим работы ’паровых турбин, Госэиергоиздат, 1955.
10. В. Г. Тырышкин, К вопросу о рациональном проектировании лопаток турбинной ступени с учетом сжимаемости, «Котло-турбостроение», 1949, № 3.
11. А. Н. Шерстюк, Осевые компрессоры (аэродинамический расчет), Госэиергоиздат, 1955.
12. Я. И. Ш н е е, Теория газовых турбин, Машгиз, 1950,
13. А. В. Щегляев, Паровые турбины, Госэиергоиздат, 1955.
14. В. В. У в а р о в, Профилирование длинных лопаток газовых и паровых турбин, Оборонгиз, 1945.
15-. J. В Пек, J. Сашек, P. Vesely, Soustavny vyzkum lopatkove ucinnosti na modelovych turbinach, Proudeni v lopatkovych strojich, Sbornik dstavu pro vyzkum stroju, 1958.
16. W u Chung-Hua, The aerodynamic problem of radially long blades in turbomachines, Chinese Journal of Mechanics, 1957, v. 1, № 1.
17. A. S t о d о 1 a, Die Dampf-und Gasturbinen, 1924.
1. М. E. Дейч, Ф. В. К а з и н ц е в, В А. Головин, Счет-io-решающее устройство для определения коэффициента потерь энергии, «Энергомашиностроение», 1959, № 3.
2. Н. А. 3 а к с, Основы экспериментальной аэродинамики, Оборонгиз, 1953.
3. Г. С. Самойлович, Е. В. Майорский, И. Неруда,
В. Стекольщиков, Малоинерционные тензометрические
*онды для исследования неустаиовившнхся процессов в турбома-иинах, «Теплоэнергетика», 1959, № 1.
4. И. Л. П о в х, Аэродинамический эксперимент в машинострое-1ии, Машгиз, 1959.
5. С. Г. Попов, Некоторые задачи и методы экспериментальной аэромеханики, Гостехиздат, 1952.
6. А. Н. П р я д и л о в, Пьезоэлектрический индикатор давления 1ля исследования настоты и характера пульсаций воздуха в тур-юмашине, «Энергомашиностроение», 1956, № 12.
7. Р. П э к х е р с т, Д. Холдер, Техника эксперимента в аэро-(инаммческнх трубах, Изд. иностранной литературы, 1955.
8. В. П. Преображенский, Теплотехнические изменения [ приборы, Госэиергоиздат, 1953.
9. А. И. Туригнн, П. В. Новицкий, Проволочные преоб->азователи и их технические применения, Госэиергоиздат, 1957.
10. А. М. Т у р и ч и и, Электрические измерения иеэлектрических 1еличин, Госэиергоиздат, 1954.
11. М. М. Фетисов, Использование .индуктивных преобразователей для идменения нестационарных давлений, Труды ЛПИ, 1955, № 17.
11*. Физические- измерения в газовой динамике и при горении, Изд. иностранной литературы, 1957,
13. У. Ф. Хилтон, Аэродинамика больших скоростей, Изд. иностранной литературы, 1955.
14. Электрические измерения, Под редакцией А. В. Френке, Госэнергонздат, 1954.
15. А. У о р а н т, И. Г е ф ф н е р, Методы обработки экспериментальных данных, Изд. иностранной литературы, 1953.
| Стра ница | Строка |
Напечатано | Должно быть | |
| 26 |
Формула (1-106) | 1 dp/ Р ' dt[ | J. *+( Р dt^{ | |
| 27 |
3 сверху | в 1659 г. | в 1755 г. | |
| 38 | 5 сверху | уравнения (1-26) | уравнения (1-28) | |
| 65 | 5 сверху | на рнс. 2-4. |
на рис. 2-3. | |
|
82 | 12 снизу |
вызывается | называется |
|
| 87 | 4 сверху | 1-М2 оо | 1 — м2 00 | |
| i-esM2 00 | 1 - ем2 00 | |||
| 144 | Рис. 4-6, обозначение горизон | *1 | ||
|
тальной оси | k 4* 1 Р —+ | |||
|
153 | 4 снизу | |||
| (Р + dp)— ~р | (p + dp)-|iip | |||
| 193 | Формула (4-53) |
Под знак корня вне t3 |
стн весь знаменатель / ^ | |
| 207 | 4 сверху | °г ~ ^ ^ tl | ¦5 1= 1 -1< 1! Iй | |
|
226 | 19 снизу | в тех | в трех | |
| 241 | 18 снизу |
Ь | и0Ь** V | |
| иЪ*** | и 8*« . U . ..... ~ f | |||
| 243 | Формула (5-46} | |||
| ^0 | V 7 |
|||
| 261 | 5 сверху | макрочастиц |
микрочастиц | |
|
261 | 7 сверху |
микрочастиц | макрочастиц | |
| 289 |
10 снизу | Reoo * 105 —2-104 | Re^ * 10*-h 2-10* | |
| 371 | Рис. 6-29 |
а — *а = 0,546; б— еа — 0,04; в — еа -= 0,16. | а — га = 0,04; б — еа =0,16; в — $а = 0,546 | |
| 391 | 1 снизу |
рис. 7-7,6. | рис. 7-6,6. | |
| 398 | 14 снизу | />4 | f <4 | |
| 403 | 6 снизу | после |
поле |
М. Е. Д е й ч —Техническая газодинамика