Скачки уплотнения
ГЛАВА ЧЕТВЕРТАЯ СКАЧКИ УПЛОТНЕНИЯ
4-1. ОБРАЗОВАНИЕ СКАЧКОВ УПЛОТНЕНИЯ
В предыдущих главах были рассмотрены свойства изоэнтропического газового потока. При этом мы изучали механизм распространения в потоке таких возмущений, которые не вызывают изменения его энтропии. Перейдем геперь к изучению конечных возмущений, распространение которых сопровождается ростом энтропии газового потока.
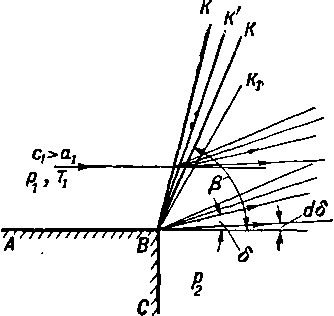
Рис. 4-1. Сверхзвуковое течение газа в область повышенного давления.
С этой целью рассмотрим движение сверхзвукового потока вдоль плоской стенки АВ, вытекающего в среду с повышенным давлением (рис. 4-1). Слева от точки В скорость будет Cj, давление рх и температура 7\. Правее точки В (за линией ВС) поддерживается давление р2, более высокое, чем рt. Если разность давлений /?2—рх мала, то в точке В возникает слабая волна сжатия В Ki
128
6П2.2 Дейч Михаил Ефимович.
Д 27 Техническая газодинамика. Изд. 2-е, переработ. М.—Л.
Госэнергоиздат, 1961
с черт. и илл. 6П2.2
design pashaok
Редактор Б. #. Шумяцкий Техн. редактор А. М. Фридкин
ГЛАВА ЧЕТВЕРТАЯ СКАЧКИ УПЛОТНЕНИЯ
4-1. ОБРАЗОВАНИЕ СКАЧКОВ УПЛОТНЕНИЯ
В предыдущих главах были рассмотрены свойства изо-энтропического газового потока. При этом мы изучали механизм распространения в потоке таких возмущений, которые не вызывают изменения его энтропии. Перейдем ienepb к изучению конечных возмущений, распространение которых сопровождается ростом энтропии газового потока.
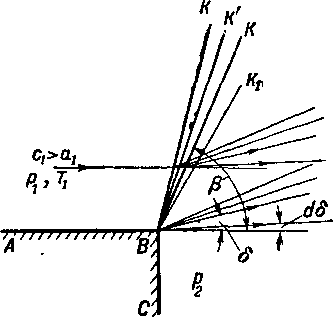
Рис. 4-1. Сверхзвуковое течение газа в область повышенного давления.
С этой целью рассмотрим движение сверхзвукового потока вдоль плоской стенки АВ, вытекающего в среду с повышенным давлением (рис. 4-1). Слева от точки В скорость будет сг, давление и температура 7\. Правее точки В (за линией ВС) поддерживается давление рг, более высокое, чем рг. Если разность давлений рг—рг мала, то в точке В возникает слабая волна сжатия ВКг-
Ёсли изменение давления в точке В станет конечным, то, как показывает эксперимент, волна переместится в положение ВК и будет обладать не бесконечно малой, а конечной интенсивностью. По мере увеличения давления рг линия ВК будет поворачиваться относительно точки В влево (ВК', ВК" и т. д.). При перех'оде через волну ВК газ сжимается и поток отклоняется на некоторый угол 8 вверх от направления невозмущенного потока АВ. С ростом
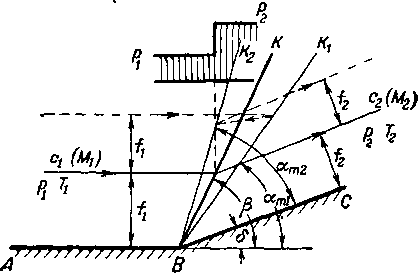
Рис. 4-2. Обтекание сверхзвуковым потоком внутреннего угла.
р2 сжатие газа в волне ВК и угол отклонения 8 увеличиваются.
Волна ВК называется плоским косым скачком уплотнения или плоской ударной волной. При переходе через такую ударную волну поток испытывает скачкообразные изменения давления, скорости и других параметров. Положение скачка определяется углом (3 между плоскостью скачка ВК и первоначальным направлением потока АВ (рис. 4-1).
Образование косых скачков уплотнения можно проследить также на простейшем примере обтекания стенки ABC, повернутой в точке В на некоторый конечный угол 8 навстречу потоку (рис.4-2).
Благодаря такому повороту стенки сечение струйки уменьшается и она суживается. В сверхзвуковом потоке это приведет к повышению давления (р2 >¦ pt). Причем повышение давления происходит скачкообразно при переходе через поверхность' ВК, являющуюся поверхностью скачка. Можно показать, что при обтекании рассматриваемой стенки непрерывный переход от параметров в области АВК к параметрам в области КВС физически невозможен.
Действительно, границей возмущения для области АВКХ должна быть звуковая волна ВКи угол наклона которой
к вектору скорости будет а == arc sin — . Вторая гра-
ница возмущения ВК2 имеет угол наклона а 2 = arc sin —.
Так как сг<С_с1 и то am2>aml. Характеристика
ВК* оказывается в невозмущенной области АВКj. и линии тока должны были бы иметь форму, показанную пунктиром, что физически совершенно нереально.
Можно предположить, что косой скачок занимает среднее положение между волнами ВКг и BKZ\ тогда угол косого скачка р связан простым приближенным соотношением с углами amV ат2 и 6:
Р ~ Т~ К>1 + ат2 + 5)'
Мы рассмотрели стационарный случай образования косого скачка уплотнения, неподвижного относительно очага возмущения.
Такой случай соответствует набеганию плоского сверхзвукового потока постоянной скорости на бесконечный клнн или движению плоского клина в среде с постоянной сверхзвуковой скоростью. При нестационарном движении скачки уплотнения могут возникать и при дозвуковых скоростях движения. В общем случае нестационарного движения ударная волна, являющаяся результатом конечного уплотнения или разрежения потока, может перемещаться относительно твердого тела, которое вызвало ударную волну.
Проанализируем условия образования таких движущихся ударных волн. Пусть в трубе постоянного сечения находится поршень (рис. 4-3). Толчок поршня вызывает слева слабую волну разрежения т' — п', а справа слабую волну уплотнения т — я. Продолжая увеличивать ско-рость'поршня толчками, мы создадим ряд слабых волн возмущений (/и,— nv ml — «j и т. д), перемещающихся в потоке газа в противоположных направлениях от поршня, каждая со своей скоростью, соответствующей скорости звука в данной области.
Нетрудно видеть, что справа каждый толчок повышает давление газа на малую величину, а слева — снижает его. Следовательно, в области III давление и температура будут выше, чем в областях II и /, 8 следовательно, и скорость звука «ni > a[I^>ai- Наоборот, в областях II', III' скорости звука будут меньше, чем в области Г (ящ < <[.вл<а1). Следовательно, справа от поршня слабые волны уплотне.
Ння нагоняют друг друга, слева волны разрежения отстают друг от друга.
Через некоторый промежуток времени волны справа сольются в одну волну, фронт которой будет границей между невозмущенной и возмущенной областями.
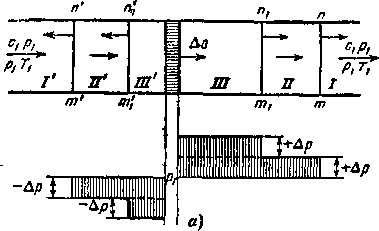
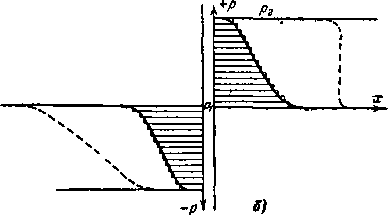
Рис. 4-3. Распространение слабых возмущений ч в трубе.
4-2. УРАВНЕНИЯ КОСОГО СКАЧКА
Как и ранее, будем рассматривать установившееся течение газа без теплообмена с окружающей средой и без трения. Предположим, что в некоторой точке сверхзвукового штока возник косой скачок уплотнения (рис. 4-4). Параметры газа до скачка обозначены индексом 1, а за скачком — соответственно индексом 2.
Рассмотрим движение газа по линии тока- ABC, пересекающей плоскость косого скачка в точке В. Как указывалось, при переходе через косой скачок линия тока деформируется, отклоняясь на некоторый угол 5. Скорость до и после косого скачка можно представить составляющими, нормальными к плоскости скачка {спХ и сп2) и касательными к ней (сп и ct2) и, таким образом, построить треугольники скоростей до и после скачка.
Очевидно, что
nl
= с2
Сп2 \
Для решения основной задачи о косом скачке, которая сводйтся к установлению связи между параметрами до и после скачка и к определению потерь, возникающих при переходе через сКачок, используем основные законы механики.
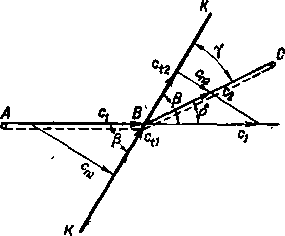
Рис. 4-4. К выводу основных уравнений косого скачка.
Закон сохранения массы — уравнение неразрывное и—для двух сечений трубки тока до и после скачка может быть записано в следующем виде:
(4-1)
PlC«l = PC„2-
Закон сохранения импульсов — уравнение изменения количества движения — в проекции на нормаль к плоскости косого скачка дает:
Pi — Pt = ?iCnl(Cn2 — Cnl)>
или
Pi + 9ic\x = Рг + Ра °2пг В проекции на плоскость скачка получим:
(4-2)
PlCnl (Ct2 ~~ Ct]) = Q’
¦ так как давление вдоль всех поверхностей, параллельных поверхности скачка .остается постоянным. Следовательно,
ct\~cn~cr (4_3)
Таким образом, касательные составляющие скоростей до и после плоского косого скачка уплотнения одинаковы.
Закон сохранения энергии — уравнение Бернулли— может быть использовано в любой известной нам форме. Рассматриваемое течение происходит без теплообмена с окружающей средой и, следовательно, полная энергия потока сохраняется неизменной:
ci I k р, _ с\ I к рг а* k + I
(4-4)
Найдем связь между скоростями. до и после скачка. Преобразуем уравнение (4-2); с учетом формулы (4-1) получим:
Р± + с2 ^l(Pz+c2\. (4-2а)
Pi Т п1 ся2 п2)
Из уравнения энергии (4-4) выразим отношение давления к плотности:
2
-4) <4’4а)
2/? - \ к — 1
И .
h ь
Подставив (4-4а) и (4-46) в уравнение (4-2а), получим: «24-г2 ) Сд1 — к~~{ c«' J
Формула (4-5) устанавливает связь между нормальными составляющими скоростей при переходе через косой скачок
И является исходной для получений зависимостей между другими параметрами течения до и после скачка.
Заменим в формуле (4-5) al по уравнению
тогда
к — 1 / cn! 1 2 \ 2 гл а\
°n\ Cn2~k + 1 ^2 а\ ’
k — 1 / cn2 I 2 \ 2 /Д й \
С,г\Сп2— Г+\[ ? l)a2> (4_ба)
или, выражая скорость звука через давление и плотность а% = k , получим:
(4-7)
Воспользуемся уравнением неразрывности (4-1); возведя в квадрат обе части этого уравнения:
г 2 2 2
Pi сп\ Рг сп2
и заменив
получим:
,2 ,2
/г! „ ьпЪ
С
АРх-^=ЛР.-^-- (4-8)
°1 а2
Исключая последовательно из уравнения (4-7) с помощью уравнения (4-8) и р2 или jt?j и ра, приходим к выражениям
Из уравнений (4-6) и (4-ба) можно получить:
Л
Ln\
к ¦
2k
п\
Из треугольников скоростей на скачке следуют очевидные соотношения:
¦¦ сх sm р;
* п\
(4-12)
сп2=с. sinT; с == Сх COS Р =
где
Тогда из уравнения (4-11) совместно с формулами (4-12)
можно получить:
k — 1 о
(4-1 la)
¦ 2~Mi sm2ft+l
k — \ sin2 p — 1
или
l~k+l^ cos^ sin2 p
(4-116)
Уравнения (4-9) и (4-10) совместно с уравнениями (4-11) и (4-12) после несложных преобразований дают искомые зависимости:
Се k — ¦" 1 / 2Й | >2 • п л 4 \
-'- м sin2 8 — 1 —
k+ 1
1 I2 cin! ft
Pi 2 1 k— 1, ,
-j- • —^-4-1 1 —¦ 7ПГТ ^-l cos2 P
k — 1 Л42 sin2 p T fe + 1 i f
Из уравнения состояния легко найти отношение абсолютных температур до и после скачка:
7*2 Р2Р1 JP1P2 '
После подстановки ^ ш получаем:
uotvn — И
Pi
Г2 k — \^(2k
T-=\rzif
-2---ИУ
Г, -|-1у уб / у^—*.M[Sin2p J
(4-15)
«Формулы (4-5), (4-11) — (4-15) выражают изменения параметров газа при переходе через косой скачок уплотнения в зависимости от показателя k, скорости потока до скачка Мг и угла косого скачка р. Эти формулы вместе с тем вскрывают основные физические свойства косого скачка. Так, из формулы (4-13) можно заключить, что нормальная составляющая скорости до скачка больше критической скорости. Действительно, так как —>1 и
Р1
с2
. « о ьп 1
М, sm2 р = -у-, заключаем, что
а\
2k ( 4i k-
>1
*+1 V а? 2й и, следовательно,
п\
, Нормальная составляющая скорости за скачком меньше критической скорости:
СП2 ^ а*'
Из формулы (4-13) следует, кроме того, что угол косого скачка больше угла характеристики ат1.
Рг Рг __ 1
Р~ Pi Т1
В этом случае косой скачок вырождается в слабую (звуковую) волну уплотнения (слабый скачок) и угол отклонения потока стремится к нулю.
Связь между углами р и 5 устанавливается по уравнению (4-6), которое можно преобразовать к виду:
k+l^-Tk-l 4, /
Но на основании формул (4-12)
сп2 _ Сп1 ct _ tgf _ tg (Р — с
(4-16)
°п\ ct сп\
Следовательно,
tg(p -S) __k-_\
‘gP Й + Ч k—\M\ sin21
Вспоминая, что
получим:
sin2 p —:
(4-17)
-i- - sin2 f +
tg
На рис. 4-5 представлены графики 8({3) при различных значениях для 6 = 1,3. Отметим, что с увеличением скорости невозмущенного течения увеличивается максимальный угол отклонения потока 8 . Следует подчеркнуть, что в соответствии с двойственным решением уравнения (4-17) одному значению угла отклонения потока S соответствуют два различных значения р. Опыт показывает, что плоскому косому скачку отвечает только меньшее значение р.
Щ
ВьШе в предположении, что скаЧоК занимает среднее положение между характеристиками невозмущенного и возмущенного потоков, была дана формула
Р ~ 4"(ат1+ат2 + 5)- (4-17а)
Сравнение этой формулы с точным выражением (4-17) для нескольких значений приведено также на рис. 4-5. Кривые показывают, что с увеличением скорости перед скачком расхождение между результатами расчета по
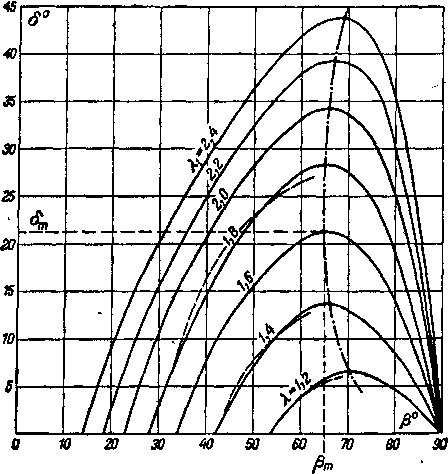
Рис. 4-5. Зависимость между углом отклонения потока и углом скачка при различных скоростях невозмущен-ного потока (для k = 1,3).
--точная формула (4-17);---приближенная формула
(4 17а).
точной и приближенной формулам увеличивается. Величина погрешности зависит также от 8.
Из уравнения (4-17) следует, что 8 = 0 при Р = ат1 и
при р = -^-. Таким образом, кривая 8 = 8(fi) имеет "Макси-
кум, положение которого определяется обычным способом. Продифференцировав уравнение (4-17) и приравняв производную нулю, после преобразования получим:
sin2p„
4 "Jl
kMi
(4-18)
+
16 ivJl
уr (*+!)(
где — угол косого скачка, соответствующий максимальному углу отклонения потока 6
Отсюда следует, что при Mi = 1 угол Рт = ~, а при
М1 = оо угол Pm = arcsin {^f j • Для промежуточных значений угол Рт с ростом Мг вначале уменьшается, а затем несколько возрастает.
Уравнение (4-11а) позволяет проследить изменение скорости потока за косым скачком М2 в зависимости от Мг и р. С увеличением р (при постоянном Мг) М3 уменьшается: перепад скоростей в скачке увеличивается.
При некотором значении = скорость за скачком становится звуковой (М2=1). При дальнейшем увеличении (3 течение за скачком будет дозвуковым.
Величину р* можно определить по уравнению (4-11 а), подставляя /И2=1. Тогда после преобразований получим:
kMf
k +1 16
< + k
')
М
(4-19)
¦М,
16
+ J/^ (^+J)
Заметим, что при М± = 1 угол = [Зт = при Мх-
= оо угол p* = pm = arcsin(}/^r-).
максимальный
Последнему значению р* отвечает угол 8 , определяемый из (4-17):
:агс
Для значений А^<оо угол |im>[5* и, следовательно, М2т<1. Это означает, что при максимальном угле отклонения потока скорость за скачком будет дозвуковой. Так как, однако, для всех Мг углы рт и fL весьма близки, то в первом приближении можно считать, что максимальный угол отклонения для каждого значения скорости невозмущенного потока достигается при звуковой скорости за скачком (Мг^ 1).
Мы установили, что параметры течения за косым скачком зависят от угла косого скачка р. При увеличении [В давление, температура и плотность газа за скачком увеличиваются (параметры потока до скачка предполагаются неизменными), а безразмерная скорость уменьшается. Угол отклонения потока, как было показано, вначале увеличивается (при (3<^т), а затем уменьшается (при pi>-j5m).
В частном случае [3 = -^- изменения параметров в скачке
оказываются максимальными, а угол отклонения 8 = 0. Такой скачок расположен нормально к направлению скорости невозмущенного потока и называется прямым скачком.
Прямой скачок является частным случаем косого скачка; основные уравнения прямого скачка получаются из формул
(4-11) — (4-15) после подстановки Р =
Изменения давлений и плотностей в прямом скачке найдем из формул (4-13) и (4-14):
h
Pi
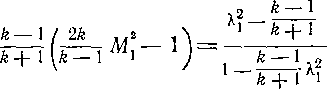
(4-20)
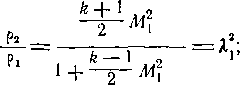
отношение температур — из формулы (4-15):
Безразмерная скорость за прямым скачкок кожет быть получена по формуле (4-11а):
^l + jTTT ^2=-2k -
^
к— 1/и1 или по формуле (4-116)
КК = 1. (4-24)
т. е.
с1с2=а\ (4-24а)
Мы видим, что произведение скоростей до и после прямого скачка равно квадрату критической скорости. Отсюда прежде всего следует, что скорость газа за прямым скачком всегда меньше критической скорости (с2<<а*).
Формулы (4-20) — (4-23) показывают, что интенсивность прямого скачка увеличивается с ростом скорости невозмущенного потока Mt (или >Ц). Отношение плотностей при максимальной скорости стремится к конечному пределу
Ит—=-
1 к—1
а отношения давлений и температур возрастают безгранично.
Необходимо иметь в виду, однако, что при больших сверхзвуковых скоростях, когда в результате скачков температура и давление газа повышаются весьма сильно, полученные формулы являются приближенными, так как они не учитывают развивающейся зависимости теплоемкости от температуры, диссоциации молекул и отклонения свойств реальных газов от свойств совершенного газа, состояние которого описывается уравнением (1-1).
Формулы косого скачка могут быть преобразованы к виду, удобному для анализа влияния физических свойств газа (показателя k).
с
С этой целью введем безразмерную скорость ? = - и выразим
?макс
показатель изоэнтропического процесса через максимальную скорость 2 k + 1
макс k — 1 '
^макс + 1
макс
Заменив k в уравнениях (4-13) и (4-14) его значением, получим:
Рг _^макс ~~ 1 Sin2 g _ 1
п т» 2 1 tl2
^ Лмакс —^_1 макс
(4-13а
Ь
X2
р2 __ макс
(4-14а
+ Si sin2
Скорость за скачком выражается уравнением [формула (4-116)]
}2 {-2 к2 «2
-Г2---I2-—COS50?+/(?„ Р). (4-116)
h ?1
где
—2 cos-’ji
/>. Г \ 1
f («1> Ю sin2 ji X4
макс
Как видно, каждая из приведенных формул содержит два сомножителя, один из которых зависит только от ^ и р и не зависит от k, а второй является функцией только k.
Такая структура формул скачка позволяет приближенно оценить влияние изменения физических свойств газа и производить расчет параметров косого скачка при различных постоянных значениях k*.
Для определения других параметров скачка можно пользоваться очевидными соотношениями- Отношение температур
Г» 1-5*
Угол скачка
1-5?
tgP=| 1+-^"ЖТГ 1*8»
sm2B ьчг
г / макс
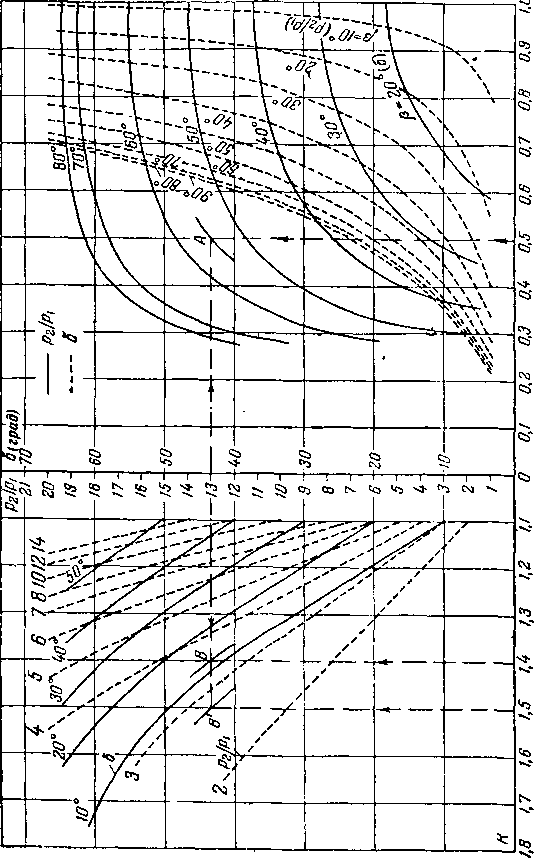
Рис. 4-6. Влияние показателя k на интенсивность косого скачка.
Для расчета скачков при различных k могут быть построены графики p2/Pi в зависимости от g,, (I (или 6) я k (рис. 4-6). Влияние k можно оценить при одинаковых р или 3. Сравнение при одинаковых р показывает, что с уменьшением k интенсивность скачка возрастает.
4-3. УДАРНАЯ ПОЛЯРА
Зависимость между параметрами на скачке можно в весьма удобной форме представить графически. С этой целью рассмотрим треугольники скоростей на скачке (рис. 4-7).
Расположим вектор скорости до скачка сг по оси х (отрезок OD). Отрезки OF и FD представляют собой соответственно касательную ct и нормальную сп1 составляющие скорости до скачка. Зная угол отклонения потока 8,
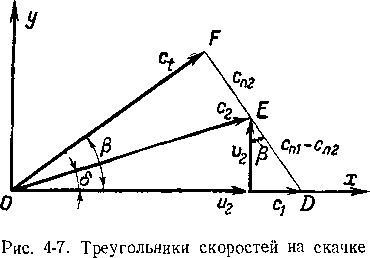
проведем линию вектора скорости за скачком сг до пересечения с отрезком FD. Точка пересечения (точка Е)определяет величину вектора са, а отрезок EF выражает нормальную составляющую скорости за скачком.
Вектор скорости с2 можно представить двумя другими составляющими: «а и vt. Компоненты ы2 и v2 являются проекциями с2 на направление скорости потока перед скачком и на нормаль к этому направлению.
Найдем уравнение кривой, описываемой концом вектора скорости за скачком с2, при постоянном значении вектора скорости перед скачком сг и переменных значениях угла поворота потока за скачком 8.
Выражая это уравнение в форме связи между ыа и vs, мы получим кривую скорости за скачком в плоскости годографа скорости.
Для получения искомой зависимости используем основное уравнение косого скачка (4-5). Подставив в это уравнение значения сп1 и ct из формул (4-12), получим:
с, sin р ^ sin р - = а-щ±с] cos2 р, (4-25)
так как (рис. 4-5)
= at lV2 + (Cl — “*) Ч - k+1 ClVr
Окончательно
a2
*
o! = (Ci —--- • (4‘26)
К 2
77+F+lCi~~ u*
Кривая, отвечающая уравнению (4-26), представленная на рис. 4-8, называется ударной полярой. Кривая при надлежит к классу гипоциссоид. Ударная поляра может быть широко использована для расчета косых скачков графоаналитическим методом и для выяснения некоторых особенностей таких скачков.
Обратимся прежде всего к предельным значениям и2, даваемым уравнением (4-26).
Легко видеть, что у2 = 0 при
И2-С \
и
г
Первый случай (и2 = сt) отвечает бесскачковому процессу; косой скачок уплотнения переходит в волну слабого возмущения (характеристику). Касательные к гипоциссоиде в точке D расположены под углом aml = arcsin
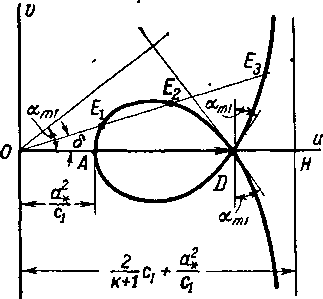
Рис 4-8. Ударная поляра в плоскости годографа.
к вектору с1. Заметим, что эта точка является одновременно точкой диаграммы характеристик и ударная поляра здесь переходит к эпициклоиду.
Второй случай (uic1=a2) характеризует переход косого
скачка в прямой скачок, угол которого = Этому случаю на гипоциссоиде отвечает точка А.
Из уравнения (4-26) следует, что и2 может обратиться в бесконечность при
_ 2 I
—6 + lCl + с, •
Очевидно, что ветви гипоциссоиды асимптотически приближаются к прямой, проведенной параллельно оси v на
— °2 2
расстоянии ОН =
~-г]ci от начала
координат. Эти
ветви не имеют физического смысла, так как они дают значения скорости за скачком (точка Е3 на рис. 4-8), большие, чем до скачка. Таким условиям отвечал бы скачок разрежения, но скачков разрежения существовать Me Mokef. Отбрасывая внешние ветви гипоциссоиды как физически нереальные (см. ниже), мы замечаем, что ударная поляра в пределах между крайними точками А и D дает два значения для вектора скорости за скачком.
Обычно плоские скачки реализуются при значениях вектора скорости потока за скачком, отвечающим точкам Е2 (рис. 4-9,а). Второе значение скорости с2, соответствующее
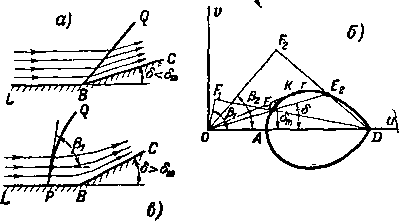
Рис 4-9 Отрыв и искривление скачка уплотнения
точкам Еj, в плоском скачке может быть реализовано лишь при специальных условиях.
Рассмотрим сверхзвуковое течение газа вдоль стенки LBC (рис. 4-9,а), постепенно увеличивая угол отклонения потока 8 (угол поворота стенки в точке В). При малых значениях 5, близких к нулю, возмущение потока невелико и скорость за скачком с2 близка к скорости до скачка сг. По мере увеличения § точка Ег (рис. 4-9,6) перемещается вдоль ударной поляры от D к г, где точка г дает скорость за скачком М2 = 1. Дальнейшее весьма небольшое увеличение 8 приводит поток за скачком к состоянию, определяемому точкой К. Здесь течение за скачком уже дозвуковое (М2<^ 1) и § достигает максимального значения 5т>
На рис. 4-10 представлено обтекание клина сверхзвуковым потоком. Если половинный угол раствора клина 8 меньше Ьт для данной скорости Мг, то на носике клина возникают два прямолинейных косых скачка: АВ и АВ,, образующих так называемую головную ударную волну клина.
При дальнейшем увеличении угла 8>8т скачок отходит от передней точки и искривляется (рис. 4-9,б). Это объясняется тем, что скорости распространена возмуЩё-ний становятся больше скорости потока. Действительно, увеличивая угол поворота стенки 8, мы тем самым увеличиваем поджатие потока, т. е. его давление, плотность и температуру. Вместе с тем растет и скорость распространения возмущений, равная скорости звука возмущенного потока a^^^kgRT^. При о]>оп эта скорость становится больше скорости потока и поэтому возмущения проникают вперед по потоку. Однако при удалении от стенки ВС (рис. 4-9,б) давление, плотность и температура
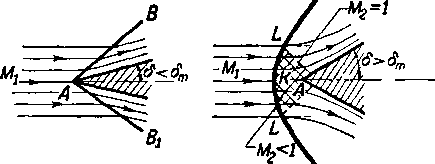
a) N б)
Рис. 4-10 Обтекание клина сверхзвуковым потоком.
будут уменьшаться; вместе с тем будет падать и скорость распространения возмущений. На некотором расстоянии от стенки возникнет геометрическое место точек PQ (рис. 4-9,в), в которых скорость распространения возмущений снизилась до скорости потока. Очевидно, за пределы этой поверхности возмущения, вызванные стенкой, не смогут проникнуть, так как они будут сноситься потоком назад. Поверхность PQ отделяет зону невозмущенного потока от зоны возмущенного потока и представляет собой отошедший скачок уплотнения.
Следовательно, если 8 >¦ Ът, то плоский косой скачок сменяется криволинейным скачком (рис. 4-10), который располагается не на носике клина, а на некотором расстоянии перед ним. Это расстояние зависит от скорости невозмущенного потока УМ, и 8. С ростом М1 скачок приближается к носику тела. С увеличением угла отклонения при 8>8т екачок удаляется от тела. Обтекание скругленного но-'€ика тела сверхзвуковым потоком всегда будет происходить с образованием криволинейной головной волны, отор-
вавшейся от носика, а расстояние между волной и носиком для центральной линии тока будет зависеть от скорости Мj и от формы носика.
Заметим, что при 8 = §т поток за скачком дозвуковой и Мг несколько меньше 1 (точка К на рис. 4-9,6). Так как для нейтральной линии тока, разветвляющейся в точке А
(рис. 4-10), р = -^- и 2 = 0, то элемент скачка, пересекающий эту линию, должен быть прямым. Скорость потока за элементом прямого скачка определится точкой А на ударной поляре (рис. 4-9б,). Поток за скачком на этой линии тока всегда дозвуковой.
Все участки скачка, кроме центрального, расположены под различными углами к вектору скорости невозмущенного потока •
Рассматривая такую искривленную головную волну, ' состоящую из большого числа малых прямолинейных элементов, можно убедиться, что по мере удаления от центральной линии тока уменьшается и угол наклона элементов скачка р . При этом можно воспользоваться ударной полярой для расчета потока за скачком для каждой линии тока в отдельности Участку головной волны KL отвечают точки ударной поляры от Л до г, в которой скорость М3 = 1. На этом участке поток за криволинейным скачком будет дозвуковым. Следовательно, если головная волна отрывается от тела, то в некоторой области, прилегающей к носику тела, течение будет дозвуковым (эта область на рис. 4-10,6 заштрихована), а линии тока здесь будут иметь разную кривизну. В различных точках за скачком давления будут различными.
По мере удаления от точки К уменьшается наклон элементов скачка и вместе с тем уменьшается интенсивность скачка. В некоторой точке L скорости за скачком становятся звуковыми. Выше этой точки состояние за скачком определяется отрезком ударной поляры от г до D. На бесконечном удалении от тела криволинейный скачок вырождается в слабую волну уплотнения, которой отвечает точка D на ударной поляре.
Таким образом, если происходят искривление и отрыв скачка от носика тела, то каждая точка ударной поляры характеризует состояние за скачком только для одной
линии тока, а не для всей области течения, как это имеет место в случае плоского скачка. Следовательно, криволинейному скачку в целом соответствует не одна точка гипоциссоиды, а вся ее ветвь AD.
В табл. 4-1 приведены значения Ьт для двух значений &=1,4 и 1,3. Значения 8т зависят от числа М1(Х1) и физических свойств газа (k) и могут быть определены по уравнению (4-17) при условии подстановки в него Р = Рт из уравнения (4-18).
Таблица 4-1
Значения максимальных углов отклонения потока в плоском косом скачке уплотнения
| k = 1,4 | k = 1.3 |
k = 1,4 |
k ~ 1,3 | ||
| ьт |
К | ||||
| 1 | 0 | 0 |
1,7 | 25° 15' |
24°42' |
| м |
5°25' | 5°14' | 1.8 | 28°55' | 28° 18' |
| 1,3 | 9°41' |
9° 30' | 1,9 | 32° 00' | 31°30' |
|
1,4 | 13°55' |
13°24' | 2,0 | 35°00' | 34° 18' |
| 1,5 |
18°00' | 17°30' |
2,2 | 40° 15' | 39°40' |
| 1,6 | 21 °41' |
21°15' | 2,4 |
45°00' | 43°50' |
4-4. ИЗМЕНЕНИЕ ЭНТРОПИИ В СКАЧКЕ
Как известно из термодинамики, для элементарного процесса без теплообмена с окружающей средой, происходящего в совершенном газе, изменение энтропии определяется уравнением
Интегрируя это уравнение, получим
![]()
![]()
Для обратимого (изоэнтропического) процесса Д« = 0 и
![]()
Посмотрим, как изменяется энтропия при переходе через скачок уплотнения. Исключив из уравнений (4-13) и (4-14) iWjSin2p, получим:
Рг — k— Г Pi
k -f- 1 р2 1 — U 1 ’
(4-28)
Р1 h__k + 1
Pi k — 1
Произведя расчет, легко убедиться, что для скачка
уплотнения, для которого —>>1, всегда
Pi
![]()
и, следовательно, согласно (4-27) при переходе через скачок энтропия газа возрастает.
Увеличение энтропии при переходе через скачок объясняется необратимым характером изменения состояния газа в скачке, „ударным* характером процесса. В результате такого процесса часть кинетической энергии газа необратимо переходит в тепло; при отсутствии энергетического обмена с внешней средой внутренняя энергия потока необратимо возрастает. Кривую, характеризующую процесс, протекающий по уравнению (4-28), называют ударной адиабат о^й.
Для скачка разрежения —<<1 и < 1 получаем
Pi Р1 \ Рг
As < 0, что невозможно при отсутствии энергетического обмена с внешней средой, так как противоречит второму закону термодинамики. Отсюда следует, что скачки разрежения в энергетически изолированном течении не могут возникнуть, так как это противоречило бы второму началу термодинамики. Однако, как показано в гл. 3, в сверхзвуковом течении волна разрежения с непрерывным падением давления представляет собой вполне устойчивое явление; энтропия при переходе через такую волну сохраняется неизменной.
Изменение энтропии в скачке уплотнения может быть выражено через параметры Мг и В путем замены в уравнении (4-27) — и -г по формулам (4-13) и (4-14); тогда
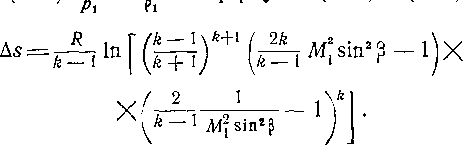
(4-29)
Уравнение (4-29) позволяет заключить, что изменение энтропии в косом скачке зависит от скорости невозмущенного потока Мj и угла косого скачка р.’ При неизменной скорости М, энтропия при переходе через скачок меняется в соответствии с изменением угла р. Если скачок прямолинейный и, следовательно, вдоль скачка {3 сохраняет постоянное значение, то для всех линий тока, пересекающих скачок, изменение энтропии будет одинаковым. Если же скачок криволинейный, то увеличение энтропии для каждой линии тока будет различным, так как вдоль скачка угол р меняется. Это означает, что за криволинейным скачком поток будет вихревым; за прямолинейным скачком течение остается потенциальным.
Пользуясь уравнением (4-28), можно рассмотреть изменение состояния г^за при переходе через слабый скачок. Полагая рг = р, Pj = р и считая, что давление и плотность в скачке изменяются на бесконечно малую величину, т. е.
P»=P + dp; pa = p-fdp;
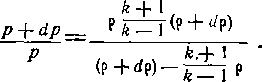
из (4-28) получим:
Отсюда, пренебрегая бесконечно малыми второго порядка, Приходим к уравнению изоэнтропического процесса:
Р Р '
Таким образом, изменение состояния 6 сКаЧке бесконечно малой интенсивности (слабый скачок) является изоэнтропи-ческим.
4-5. ПОТЕРИ В СКАЧКАХ УПЛОТНЕНИЯ. ПОСТРОЕНИЕ ПРОЦЕССА В ДИАГРАММЕ i-s. СКАЧКИ УПЛОТНЕНИЯ В РЕАЛЬНОМ ГАЗЕ
Рассмотрим более подробно энергетические преобразования в скачках. Предполагая энергетически изолированное течение, заключаем, что полная энергия потока при переходе через скачок не меняется. Это значит, что
2 2
CI I k Р] _ с2 I k рг
2 ' k — 1 2 1 k — 1 р2 ’ или, пользуясь параметрами полного торможения,
Еп = Р™ . (4-30)
Pol Ро2
Условие (4-30) можно заменить эквивалентным условием постоянства энтальпии торможения при переходе через скачок:
г‘о; = г'о2 = (4-30а)
или при
с.
, = const; 1
-т -т (4-306)
01-1 02-1 0‘ »
Имея в виду эти условия, рассмотрим процесс скачка в диаграмме is (рис. 4-11). Зная давление торможения до скачка р01 и энтальпию торможения г0, найдем в диаграмме is точку О j, характеризующую состояние изоэнтропи-чески заторможенного газа до скачка. По известной скорости потока до скачка ct или давлению рх находим точку D, которая определяет состояние движущегося газа перед скачком. В скачке статическое давление потока увеличивается до р2. Если известен угол отклонения потока 8 и, следовательно, р, то Состояние газа за скачком определено (точка Ег на рис. 4-11), так как по формуле (4-29) можно найти приращение энтропии As51. Заметим, что линия, соединяющая точки D и Е2 на рис. 4-11, не характеризует изменения состояния газа в скачке, так как в диаг-
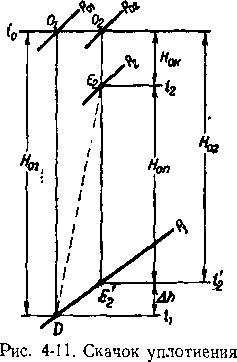
в тепловой диаграмме.
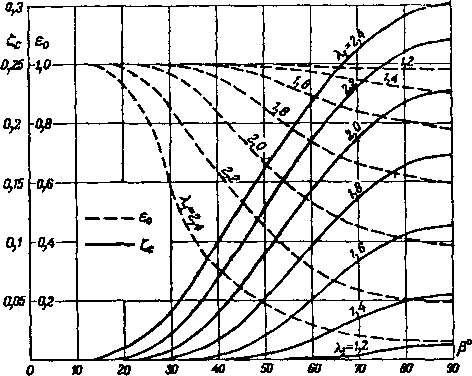
Рис. 4-12. Коэффициенты потерь и отношение давлений торможения на скачке в зависимости от угла р и скорости невозмущенного потока.
рамме is неквазистатические процессы могут быть представлены только начальной и конечной точками процесса.
Если поток за скачком изоэнтропически затормозить, то состояние полного торможения характеризуется точкой 02, в которой легко находится значение р02. Если предоставить теперь потоку возможность изоэнтропически расшириться до давления перед скачком, то его состояние будет определено точкой Е'2 . Скорость газа при этом может быть вычислена по уравнению энергии:
Aci2 .,
~2g~ ^2 ^02
где Я0з — изоэнтропический перепад энтальпий за скачком. Величину Я02 можно рассматривать как сумму
^02=-^Ок +^0П’
где Я0к — кинетическая энергия потока за скачком:
тт __^2_ .
П0к — 2g ’
я0п — изменение потенциальной энергии потока в скачке: Очевидно, что
Я0 2 Яо 1 >
где Hoi = ~2^~—изоэнтропический перепад энтальпий до скачка.
Потери кинетической энергии в скачке будут:
Ah = H01 — H0z = ^ (cf — с\ ),
где Д/г легко определяется по диаграмме is как разность энтальпий i2 — г\.
Потерю энергии нетрудно связать с основными параметрами скачка. Выразим
к-i г..
так как
(4-32)
Я0
ft-i р±\ к
Ро2 Рп_Роз
Yol Yo2
Введем понятие коэффициента потерь энергии в скачке-A h , Я0
Я01 1
ft—1
ft
тогда после подстановки Я01 и Я02 получим:
(4-33)
'к— 1 м\
или с помощью (2-21)
Г k+l J__1 1 Г / Pol',52-1 _ 11 .
(4-ЗЗа)*
Отношение ~—е0 характеризует изменение давления
полного торможения в скачке. Эту величину можно представить в зависимости от параметров скачка М1 и р.
Так как
/)02__ Рг Ро2
Pi ~ Pi Pi’ то- из (4-13) и табл. 2-1 получаем:
Отсюда с помощью (4-11а) получаем:
6+1 _А_
![]()
?0 — k
![]()
Представим в зависимости от тех же параметров скачка коэффициент потерь в скачке ?е, используя формулы (4-33) и (4-35):
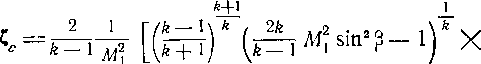
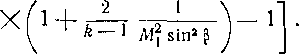
Заменив число Mt через Я1 по формуле (2-21), получим зависимость в виде:
(4-36)
С* =?(*», р).
На рис. 4-12 представлен график е0 и в косом скачке в зависимости от угла р и безразмерной скорости невозмущенного потока 4 для k = l,3. Из графика видно, что коэффициент потерь интенсивно возрастает с увеличением угла косого скачка и с ростом скорости Я,, достигая максимальных значений при р = -^- (прямой скачок).
При обтекании тела сверхзвуковым потоком перед телом возникает ударная волна (скачок уплотнения); при переходе через эту волну энтропия газа растет, а скорость уменьшается.
Таким образом, в сверхзвуковом потоке идеальной жидкости появляется особый вид сопротивления — волновое сопротивление, зависящее от потерь в скачках, а следовательно, от формы и интенсивности скачков. Как мы видели, форма скачка и его интенсивность зависят от формы тела и скорости обтекания. Учитывая, что при уменьшении угла отклонения 8 (а, следовательно, и (3) потери в скачке уменьшаются, можно заключить, что остроконечные тела в сверхзвуковом потоке должны обладать меньшим сопротивлением, чем тела, имеющие скругленную форму.
Изменение потерь в скачках в зависимости от их интенсивности можно проследить в тепловой диаграмме. Построе-
Мне „ударной поляры* в тёпловой диаграмме удобно выполнить следующим образом1.
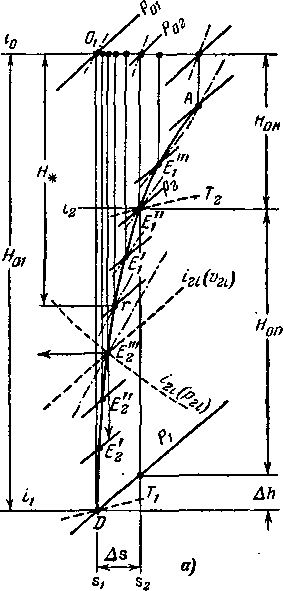
По параметрам до скачка рх и 7\ находим точку D (рис. 4-13) и при известной скорости сг точку Ог Задаемся
- о п .1
рядом значении р в пределах от р = —. Для каждого значения ,3 определяем
arcsra-
до
Я,
Ок
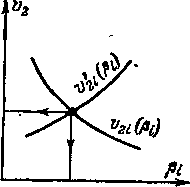
Рис. 4-13. Построение в тепловой диаграмме линия изменения состояния газа, соответствующей ударной поляре.
М,
~. Для каждого значения ,3 определяем — « Т*
Z р j
носим в диаграмме is точки Е'2 , Е” и т. д. до точки А, которая соответствует прямому скачку. Геометрическое место этих точек дает состояние газа в координатах is, соответствующее ударной поляре. Заметим, что полученная
кривая должна быть касательной к линии изоэнтро-пического изменения состояния О,D, так как при бесконечно малых возмущениях потока энтропия газа остается постоянной.
Для каждой точки кривой (например, Е") легко определяются: кинетиче
ская энергия за скачком
, изменение’ по-
1 Соответствующая кривая в диаграмме is может быть названа „ударной полярой" лишь условно, т. к. она не является векторной кривой. Приводимое построение справедливо для идеального газа.
тенциальной энергии в скачке #оп и потери кинетической энергии Д/г. Вместе с тем здесь можно определить и все параметры скачка: р2, Т53, р2, р02, As и тем самым существенно дополнить ударную поляру, построенную в плоскости годографа. В плоскости годографа ударная поляра дает кинематическую картину течения (поле скоростей); в тепловой диаграмме мы получаем характеристики энергетических преобразований на скачке и изменения параметров потока. На линии DA легко найти также точку г, соответствующую М2 = Я2 = 1. Для этой цели подсчитываем критический перепад энтальпий:
гг Aal k—\.
Н
—=•, , , ia. 2 g
k + 1 0
и откладываем его от линии i0= const.
Характер полученной кривой, обращенной выпуклостью к оси г, отчетливо показывает, насколько интенсивно увеличиваются потери с ростом р и приближением к прямому скачку.
Для расчета скачков оказывается весьма удобным пользоваться специальными диаграммами. Такие диаграммы позволяют легко определить характеристики скачка по двум заданным параметрам. В приложении даны диаграммы косых скачков для k = l,3 и & = 1,4*.
Способ пользования диаграммой косых скачков поясняетси иа рис. 4-14. В правом верхнем квадранте диаграммы нанесены графики Рз —
5 = 8 (Р) н -у- = р (Р\ отвечающие различным, но постоянным значениям скорости перед скачком Xj. На каждой кривой надписано значение X,; в скобках указывается та величина, которую изображает данная кривая. В левом верхнем квадранте представлены графики В = Pi —
= д(Ха) и =/>(Х2) для различных, но постоянных значений Xj. Pi
В левом- иижнем квадранте дана зависимость отношения температур
Т —
на скачке от скорости за скачком -=г- = Т (Х2). В правом нижнем квад-
11
раите нанесены кривые коэффициентов потерь энергии в скачке Кс — = ?СФ и коэффициентов восстановления давлений s0 = e0(ji). Таким образом, в качестве параметра для всех кривых диаграммы выбрана скорость потока до скачка Xv
Поясним на примере способ пользования диаграммой. Допустим, что ная известны угол отклонения линии тока S и скорость потока до скачка Xt. На кривой 8 = 8 ((1), соответствующей заданному значению Лц находим точку А. Проектируя эту точку на горизонтальную
Рг —
ось, найдем в точке Аг угол косого скачка Ца кривой — = р(?),
отвечающей тому же значению А,, получим точку А2, которая определяет отношение плотностей p2/pi- Зная А, и д, на кривой д = 5, (Х2)
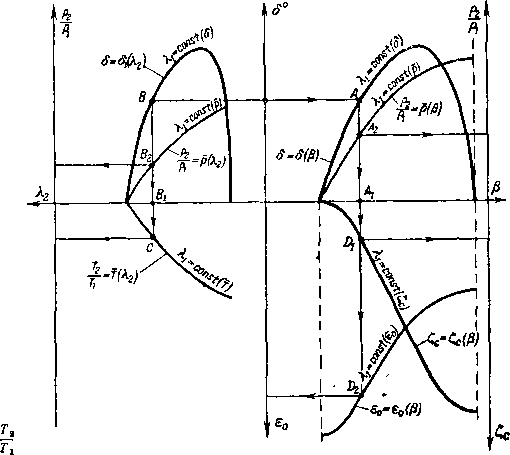
Рис. 4-14. Способ пользования диаграммой косых скачков.
в левом квадранте находим точку Bv которая определяет безразмерную скорость за скачком Х2. Перейдя при том же значении Х2 на кривую
~ — ~р (А2), получим в точке В2 отношение давлений на скачке — . Pi Pi
Т2 —
В точке С на кривой у- = Т (Х2) определяем отношение темпера-Т
тур -JT- . Проектируя точку Аг на линии = С (Р) и е0 = е0(Р) в точках D, и Пг, найдем значения коэффициента потерь энергии и коэффициента восстановления давления. Рассматриваемая диаграмма позволяет производить расчет скачков по любым двум параметрам. Так,
Рг
например, заданными могут быть: X, и — -и д; 8 и р и т. д.
Тепловая диаграмма удобна для расчета скачкой упЛотнёнйя в реальном газе и, в частности, во влажном паре и диссоциирующем воздухе Параметры потока перед скачком и угол отклонения на скачке обычно известны. Задаваясь рядом значений угла скачка Р(, нетрудно найти соответствующие значения нормальных составляющих скорости.
с j cos
с«1е =С1 SIn Рг' cn4i = ~7tg (Jt _ 8) •
По основным уравнениям (4-1)—(4-4) определяются параметры за скачком 12(, p2l и удельный объем v2l, отвечающие текущему значению Искомое решение можно наити в диаграмме i-s в точке пересечения двух кривых, одна из которых построена по параметрам i2(i p2t, а вторая—по i2(, v9l (рис 4-13,а) С диаграммы снимаются значения (2, рг, иг, действительный угол наклона скачка определяется по формуле
tg р = Ini + ,/ (jlzlLY-7,
^ 2 tg 5 - у \2Xgb)
-
где v = — .
°2
Эта же задача решается с помощью вспомогательного графика, на котором наносятся кривые v2t (Р() и v2[ (f() (ррс 4-13,б). Для построения второй кривой необходимо по диаграмме i-s перейти от значений р% и г2 к значениям v2 Решение получается в точке пересечения этих кривых, где определяются и ( и соответственно все остальные параметры за скачком В частности, скорость за скачком
сj sin р * Сг=1г sin(P-fi)-
4-6. ПЕРЕСЕЧЕНИЕ СКАЧКОВ
Рассмотрим некоторые практически важные случаи взаимодействия скачков.
Два последовательных поворота стенки ABCD (рис. 4-15,а) на угол 8 приводят к образованию двух косых скачков: ВК и СК. Угол второго скачка pa>pi, так как после первого скачка поток имеет скорость Х2<^Х1ШВ результате скачки пересекаются в точке К• За точкой пересечения оба скачка сливаются в один скачок KF. Линия тока, пересекающая систему двух скачков, деформируется, поворачиваясь в точках b и d на угол 8; при пересечении скачков скорости потока падают, а давления растут скачкообразно.
Рассматривая линию тока КН и предполагая, что проникновения частиц газа из области 4 в области 3' и, наоборот, из области 3' в область 4 не происходит, можно заключить, что в указанных областях давления и направления скоростей должны быть одинаковыми (поперечный градиент давления отсутствует). Но если предположить направление линии тока за скачком KF таким же, как и за вторым скачком СК, т. е. что суммарное отклонение линии тока составляет 28, то давления в областях 3 и 3' будут различными, так как линия тока bd прошла че-
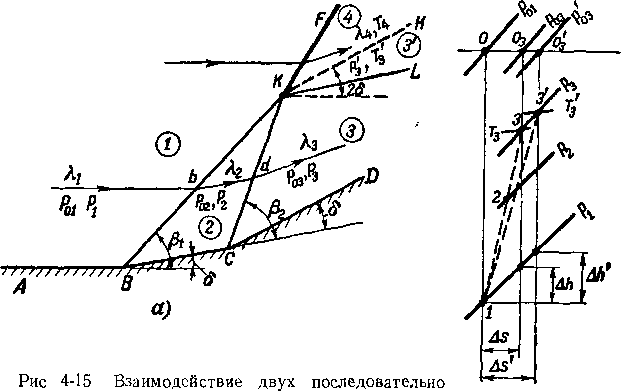
расположенйых косых скачков
рез два скачка, а линия тока КН — только через один скачок; следовательно, потери в первом случае будут меньше, чем во втором (при сжатии с бесконечным числом скачков бесконечно малой интенсивности процесс будет изоэнтропическим—без потерь), причем р3 может быть меньше или больше р3. Отсюда можно заключить, что
области течения 3 и 3' разделены слабой волной разрежения или слабым скачком уплотнения KL, при пересечении которого поток приобретает давление pi = p3. Ин
тенсивность волны KL в этом предположении легко определяется. Действительно, зная угол 8 и находим давление рА за скачком KF. Давление р3 нам известно в результате расчета скачков ВК и СК. Отношение — дает
Рз
интенсивность отраженной волны KL.
В общем случае углы отклонения потока в точках
В я С могут быть неодинаковыми. При этом в зависи
мости от соотношения углов 8j и §2 (8t — отклонение в первом скачке ВК и 8, — отклонение во втором скачке СК) и суммарного угла отклонения ^ -j- Ь2 меняются интенсивность отраженной волны KL, а также суммарные потери в рассматриваемой системе скачков. Расчеты показывают, что интенсивность отраженной волны KL, как правило, невелика и поэтому поворот потока на этой волне пренебрежимо мал, что и делает обоснованным предположение о повороте потока на волне KF на угол St —{— Sa.
В зависимости от скорости невозмущенного потока
и суммарного угла отклонения Sj —{— 8а меняется и знак
волны KL-
Характерно, что скорость за скачком KF всегда меньше скорости за скачком С К (Я4<[Я3); отсюда следует, что линия КН является линией тангенциального разрыва скорости. В вязкой жидкости вдоль КН развивается вихревое движение.
Изменение состояния газа вдоль линии тока при переходе через рассматриваемую систему скачков может быть представлено в тепловой диаграмме (рис. 4-15,6). В точке 2 определяется состояние газа после первого скачка, а в точке 3— после второго скачка, так как углы и известны. Легко определяются также все параметры за скачками: р3. Т3, Я3 и параметры торможения р03, р03.
Точка 3' на изобаре р.л дает состояние газа за скач-ком KF54. В точке 03 находим давление торможения за скачком KF р(а <Zp03. Потери энергии в скачке KF выше суммарных потерь в скачках ВК и СК, т. е. As' ]>
As. Таким образом, при заданных пределах изменений давлений торможение потока одним скачком обусловливает большую потерю энергии, чем в случае последовательного торможения двумя скачками.
Предельным случаем является торможение потока вдоль плавной вогнутой стенки, в каждой точке которой поток испытывает отклонение на малый угол d§ (рис. 4-16).
При этом у стенки образуется волна сжатия, состоящая из бесчисленного множества характеристик уплотнения. Движение газа через такую волну сжатия совершается при постоянной энтропии. Однако плавное изоэнтропиче-ское торможение здесь может происходить только в слое газа, прилегающем к стенке. В результате пересечения характеристик уплотнения на некотором расстоянии от стенки, зависящем от скорости набегающего потока, возникает криволинейный скачок переменной интенсивности.
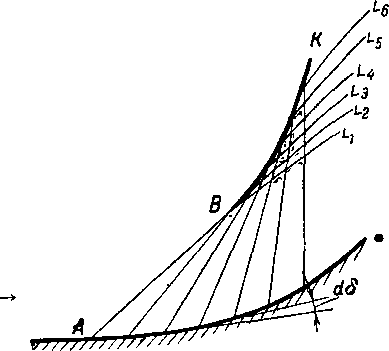
Рис 4-16 Сжатие потока при обтекании плавной вогнутой стенки
Поток за скачком вихревой, так как скорости в разных точках за линией ВК различны.
Взаимодействие волны сжатия со скачком уплотнения качественно происходит так же, как это было указано при рассмотрении взаимодействия двух косых скачков (рис. 4-15). В точках пересечения слабых волн и скачка возникают отраженные слабые волны (рис. 4-16), так как изменения давления и направления потока при переходе через волну сжатия и скачок будут различными.
В зависимости от скорости набегающего потока повышение давления в скачке может быть более интенсивным или менее интенсивным, чем в волне сжатия. Следовательно, отраженные волны могут быть либо волнами сжатия, либо волнами разрежения.
Отличный от рассмотренного случай пересечения двух косых скачков показан на рис. 4-17. Косые скачки возникают в результате поворота двух противоположных стенок канала на разные углы ^ и 8а. Направления потока в зонах II и III будут неодинаковыми-, в зоне II! отклонение будет больше на угол &2 —8Х. Параметры течения за косыми скачками АВ и АХВ легко могут быть определены по известным параметрам до скачков рх, 7\ и углам 8j и 8а, если эти углы меньше соответствующего максимального значения 8т для данного вектора скорости 11.
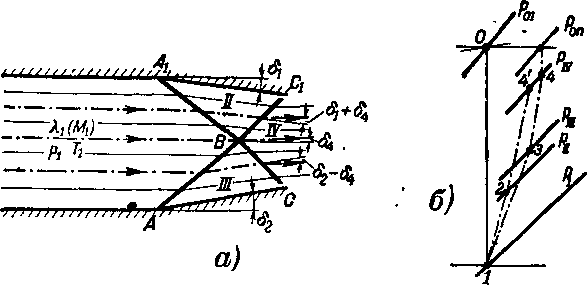
Рис. 4-17. Схема пересечения двух косых скачков.
а_нор\тлььое пересечение; б — процесс в скачках в тепловой диаграмме.
Параметры потока в области IV можно найти, исходя из граничных условий для линии тока, проходящей через точку В. Примем, что направления скоростей и давления во всех точках области IV будут одинаковыми. Отсюда определяется угол между вектором скорости в зоне IV и вектором 2j. Действительно, если результативное отклонение потока в зоне IV обозначить 84> то из рассмотрения рис. 4-17 легко установить, что отклонение потока при пересечении скачка BCt равно St —{— 84, а при пересечении ВС оно равно 82 — 84. Задаваясь различными значениями давления в зоне W (plv) по формулам (4-13) и (4-17) или по диаграммам косых скачков, находим углы наклона скачков ВС и BCt и углы отклонения потока Sj —|— и
82 — 84. Значение р]у, при котором величины 84, определенные по параметрам зон II и III, будут одинаковыми,
можно найти, построив зависимости ^ABCt и 84вс от рп. Точка пересечения этих кривых даст искомое значение 84. Зная величину 64, находим углы косых скачков рйс и (Звс.
Изменение состояния газа вдоль двух линий тока, пересекающих зоны // и III, в тепловой диаграмме показано на рис. 4-17,6. Суммарное приращение энтропии для этих линий тока будет одинаковым только в тех случаях, когда 81 = 82. Если интенсивность скачков АВ и АгВ различна, то приращение энтропии вдоль рассматриваемых линий тока будет различным (точки 4 и 4' на рис. 4-17,6).
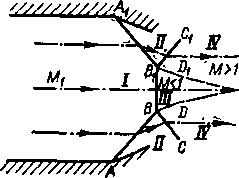
Рис. 4-18 Мостообразный скачок.
При этом, если во всех точках зоны YV давления одинаковы, скорости, температуры и плотности за скачками ВС j и ВС будут различными. Вдоль линии тока, проходящей через точку В, образуется тангенциальный разрыв скоростей, в результате чего в вязком газе возникает вихрь.
Устойчивое существование системы двух пересекающих косых скачков возможно не при всех условиях. Если углы вторых скачков рвс и |3ВС будут больше соответствующих значений Рот, характер течения меняется. Вблизи
нейтральной линии тока, проходящей через точку В, образуется криволинейный скачок. Система пересекающихся прямолинейных косых скачков переходит в мостообразный скачок (рис. 4-18). Потери энергии в потоке при этом увеличиваются.
4-7. СТУПЕНЧАТОЕ ТОРМОЖЕНИЕ ПОТОКА
Ступенчатое торможение потока можно получить, применяя различные системы косых скачков. В предыдущем параграфе было показано, что если при заданных пределах изменений статического давления увеличивать число косых скачков путем увеличения последовательных поворотов стенки, то торможение потока будет более плавным, а суммарные относительные потери будут уменьшаться.
Обычно за последним косым скачком располагают прямой скачок, на котором происходит переход к дозвуковой скорости.
Торможение потока в различных системах скачков было подробно исследовано Г. И. Петровым и Е. П. Уховым. Следуя основным выводам этой работы, рассмотрим частный случай торможения потока в двух скачках — косом и прямом.
Рассматриваемая задача формулируется так: определить угол наклона первого — косого — скачка, при котором переход от заданной сверхзвуковой скорости к дозвуковой происходит с минимальными потерями (рис. 4-19). Расчет такой системы можно осуществить последовательно, применяя диаграммы косых скачков (см. приложение). При заданной скорости невозмущенного потока Хг и выбранном значении угла 8 (или р,) легко определяются скорость Яа и давление р2 за косым скачком. Соответствующая потеря энергии или изменение давления полного торможения е01 также определяется по диаграмме косых скачков (или по формулам § 4-5).
Аналогично можно найти скорость и статическое давление за прямым скачком (Я3 и р3) и коэффициент потери энергии (или s02).
'В качестве примера на рис. 4-19 показано изменение скорости потока и коэффициентов потерь в системе косого и прямого скачков в зависимости от угла ^ для Я1 = = 2,0 (? = 1,3). Кривые показывают, что для данной скорости имеется такое наивыгоднейшее сочетание косого и прямого скачков, при котором суммарные потери будут наименьшими.
Действительно-, с увеличением угла косого скачка р, растет коэффициент потерь Сс| в косом скачке и уменьшается скорость за косым скачком Я2. Очевидно, что при 8 = 0 и Pi=aml=22°45'(дляЯ^г.О) косой скачок переходит в характеристику. В этом случае Сс1 = 0. Предельное значение угла рх, при котором еще возможно существование плоского косого скачка, составляет Pj = Pml = 65°40\ При этом значении р, поток за косым скачком имеет дозвуковую скорость. В указанных пределах изменений угла [5, (22°45' — 65°40') за косым скачком может существовать прямой скачок. При j51 = 22°45' существует только прямой скачок, а при pt = 65°40г— только косой.
Меняя в этих пределах угол косого скачка и подсчитывая Я2 и /72 (параметры перед прямым скачком), можно найти параметры газа за прямым скачком. Скорость за
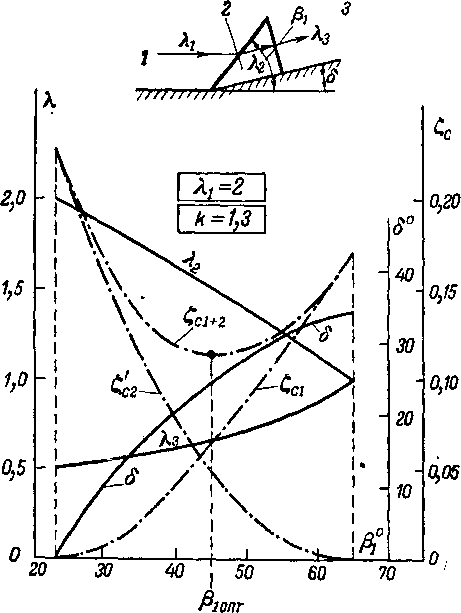
Рис. 4-19. Изменение скоростей и потерь в системе двух скачков (косой + прямой) в зависимости от угла косого скачка р t при = 2,0; k = 1,3.
прямым скачком Я3 = -^- увеличивается с ростом в пределах от Л3 = 0,5 при Pi = 22°45' до Л3 = Я, = 1 при j3x= = 65°40\
При определении коэффициента потерь в прямом скачке необходимо величину потерь относить к кинетической
где Сс2 определяется по диаграмме косых скачков для Хй. На рис.' 4-19 нанесены значения Можно видеть, что С'2 уменьшается с ростом Вг При Р1 = 22°45' С^,2 = Сс2 = = 0,227, а при р^ббЧО' С2 = °.
Коэффициент суммарных потерь в системе двух скачков, очевидно, будет равен:
энергии невозмущенного потока, т. е. подсчитывать
![]()
![]()
Кривая суммарных потерь в системе двух скачков имеет минимум при Pi = 45°. Очевидно, что значение ^ является оптимальным в отношении потерь энергии в системе скачков.
Аналогичные расчеты можно выполнить для различных скоростей Я,, определяя наивыгоднейшее значение Pi- Результаты таких расчетов даны на рис. 4-20, где суммарный коэффициент потерь Сс представлен в зависимости от угла pt для различных значений Хг. Жирными линиями проведены кривые в диапазоне углов fi„ при которых возможно существование системы косого и прямого скачков. Пунктирная линия ABCD соединяет точки, отвечающие pi = aml. Для этих точек косой скачок имеет бесконечно малую интенсивность и, следовательно, торможение потока осуществляется только в одном прямом скачке. Точки FGHJ отвечают углу = р , при котором поток за плоским скачком имеет звуковую скорость. Для р,> >Р,. кривые Сс проведены тонкими линиями. В этом случае расчет может быть приведен в предположении существования скачка, скорость за которым дозвуковая. При Pj = 90° он становится прямым. Легко видеть, что при Pj = ат1 и р1 = 90° коэффициент потерь Сс имеет одинаковое значение.
Сопоставление кривых на рис. 4-20 показывает, что оптимальные значения Р|опт зависят от скорости невозмущенного потока Хг. С ростом Х1 до некоторых пределов значения р|опт уменьшаются. Для ^ = 1,6 коэффициент
потерь при оптимальном значении $1опт = 526 составляет = 0,035. В этом случае один прямой скачок дает (точка А на рис. 4-20) Сс2 = 0,113, а один косой при скорости за скачком, равной скорости звука (точка J на рис. 4-20), = 0,073. Следовательно, переход от одного
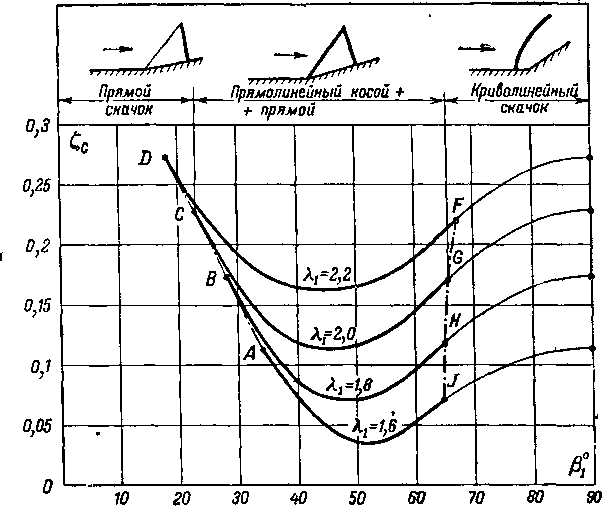
Рис 4-20 Кривые коэффициентов потерь в системе двух скачков (косой + прямой) в зависимости от угла косого скачка р., и скорости
I,; k = 1,3
скачка к системе двух скачков (косой -(- прямой) позволяет уменьшить коэффициент потерь более чем вдвое. При больших значениях Я, двухступенчатое торможение оказывается еще более эффективным.
; Следует заметить, что с ростом Я1 минимум кривых становится более пологим. Это обстоятельство позволяет выбирать оптимальные значения таким образом, чтобы и статическое давление за вторым прямым скачком было наибольшим. Отношение статического давления за системой скачков рг к полному давлению перед скачком poiможно представить в следующем виде:
Рз ___ Р2 Рг Р\ .
Poi Р\ Р2 Рт
здесь — характеризует повышение статического давления Р1
на косом, а — — на прямом скачке.
Рг
Изменение этих величин, а также еП1=^-2 и е„„ = ^-3
“ Р*1 02
в зависимости от угла косого скачка (3, для Хг = 2,0 представлено на рис. 4-21. С ростом р, отношение давлений
на косом скачке — увеличивается, а на прямом — умень-Р1 Рг
шается. График показывает, что относительное статическое давление за системой скачков для Х1 = 2,0 имеет максимальное значение при р1 = 40°, тогда как минимальная величина была получена при [3, — 45°.
Учитывая, что кривые в области минимума протекают полого, оптимальные значения можно выбирать по данным расчета восстановления статического давления в си-
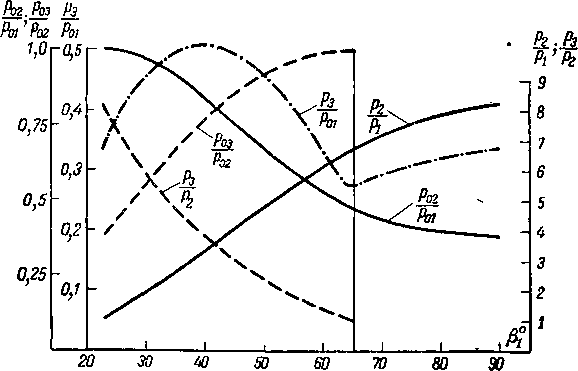
Рис. 4-21. Изменение статического давления и давления торможения в системе двух скачков (косой -f- прямой) в зависимости от угла косого скачка Pj для А., = 2,0; ft = 1,3.
М-еме скачков, т. е. принимать значения р1опт несколько меньшими, чем это диктуется кривыми
Такое решение целесообразно в том случае, когда основная задача сводится к максимальному восстановлению статического давления в системе скачков, как, например, это имеет место для сверхзвуковых диффузоров.
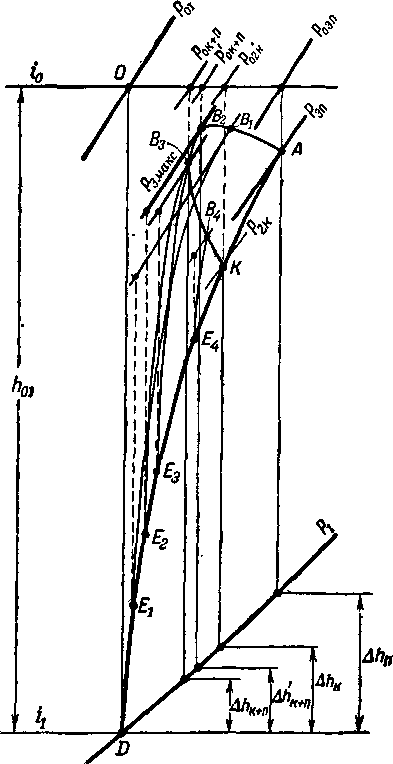
Рис. 4-22. Процесс торможения в системе двух скачков (косой + прямой) в тепловой диаграмме.
Последовательное торможение потока в системе скачков можно наглядно представить в тепловой диаграмме. На рис. 4-22 показан этот процесс для двух скачков. При р, = ат1 существует только один прямой скачок (точка Л). При pt = Pj скорость за плоским косым скачком звуковая и торможение происходит только в одном косом скачке (точка К). В пределах ат,<р,<р, может существовать система двух скачков. Задаваясь различными значениями pj (точки El — EJ, можно построить линию предельных состояний газа за системой двух скачков при различной интенсивности косого и прямого скачков (линия АВг.. .В4К)-Малым углам косого скачка отвечает верхняя ветвь кривой предельных состояний ABXBZB%. Нижняя ветвь соответствует большим углам скачка Р^Р, • Характер кривой состояний АВ1... В^К отчетливо указывает на существование оптимальной комбинации двух скачков. При некотором значении угла Р!опт потери энергии в системе скачков оказываются минимальными (точка В3). При другом, близком значении угла ^ потери несколько выше (Д/гк+п> >Д/гк+п), но статическое давление достигает максимально возможного значения /?3макс (точка В2). Линия предельных состояний может быть построена путем последовательных расчетов системы скачков.
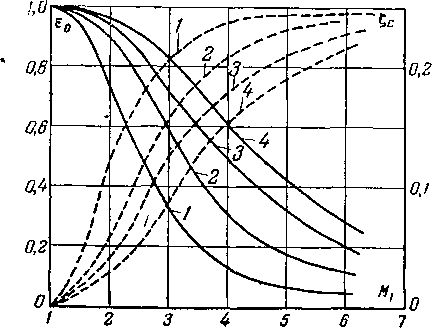
Рис. 4-23. Изменение потерь в скачках при ступенчатом торможении (цифры указывают число скачков).
Для совершенного газа можно получить уравнение этой линии в форме связи между изменением энтропии и изменением энтальпии в системе скачков.
При больших сверхзвуковых скоростях для перехода к дозвуковым скоростям целесообразно применять более сложные системы скачков, состоящие из нескольких косых и одного завершающего прямого скачка. С ростом числа косых скачков потери энергии будут уменьшаться. Для каждой скорости потока при заданном числе косых скачков существует оптимальная схема расположения скачков, которую можно найти последовательным расчетом.
Графики, приведенные на рис. 4-23, отчетливо показывают преимущество более сложных систем скачков при больших сверхзвуковых скоростях. Кривые ?с^={.(Х1) позволяют выбрать наиболее рациональную схему ступенчатого торможения для заданной скорости.
4-8. ОТРАЖЕНИЕ СКАЧКОВ
а) Отражение от твердой стенки
Рассмотрим отражение косого скачка от прямой твердой стенки, расположенной параллельно направлению скорости невозмущенного потока (рис. 4-24). Скачок образуется в
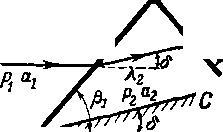
Рис. 4-24. Схема нормального отражения плоского косого скачка от твердой стенки.
А а У-тУ*8
1 fiz Л3
Рзаз
77777777777777?
А
тйчке А, где стенка поворачивается на угол 8. При переходе через первичный скачок АВ линия тока отклоняется к прямой стенке на угрл 8. Очевидно, что в точке В этот поворот неосуществим и граничная линия тока сохраняет направление стенки. Это означает, что в точке В стенка принудительно отклоняет линию тока в обратном направ-
Ленин на угол 8. В результате возникает отраженный косой скачок ВС. Заметим, что углы падающего и отраженного скачков неодинаковы, так как перед скачком ВС безразмерная скорость Я2 Л j при том же угле отклонения 8. Из графика (3 = /(8, Хг) (рис. 4-5) видно, что угол
Расчет отраженного скачка не встречает затруднений. Зная параметры [_невозмущенного течения А,, рг и угол
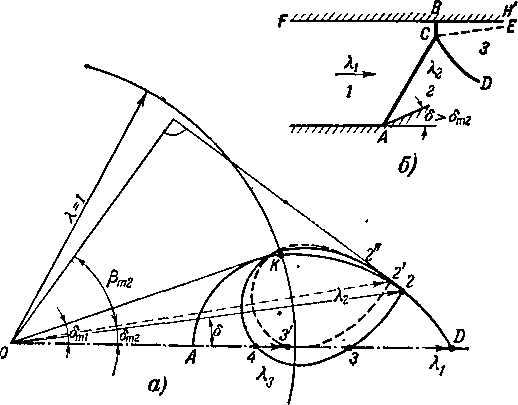
Рис 4-25. Анализ отражения скачка в диаграмме ударных поляр.
а—определение углов и скоростей при неправильном отражении; б — А-образный скачок при отражении.
отклонения 8, с помощью диаграммы скачков легко определяем параметры потока за первичным скачком: Я2, рг и (За. При том же значении 8 находим состояние газа за отраженным скачком: Яа, ps и (53. Изложенным выше способом находим потери энергии в первичном и отраженном скачках. Следует иметь в виду, что такое отражение косого скачка возможно не всегда. Если "уго'л отклонения 8 больше максимального значения для скорости А2, то картина отражения меняется. Допустим, что в диаграмме ударных поляр (рис. 4-25,а) отрезок OD изображает скорость потока до скачка А,. Если угол отклонения стенки 8<8ш2, то гипоциссоида, отвечающая скорости за скачком Яа (отрезок 02), пересекает линию вектора (точки 3 и 4).
При 8 = Ьт2 линия OD касательна к ударной поляре Я2 (точка 3'). Картина течения при этом остается прежней (рис. 4-24). Вектор скорости за вторым скачком 03' (Я3) будет меньше единицы (скорость дозвуковая).
Если 8>8т2, то ударная поляра, построенная для скорости *2, не имеет общих точек с вектором OD и отраженный скачок не может обеспечить выравнивание потока. Часть потока, прилегающая непосредственно к стенке, становится дозвуковой. Отраженный скачок CD искривляется и сдвигается против течения. При этом деформируется и первичный скачок АВ. Элемент СВ этого скачка становится нормальным к стенке, система скачков приобретает Я-образную форму. За участком прямого скачка поток дозвуковой. За криволинейной частью отраженного скачка поток может быть сверхзвуковым. В результате образуется линия тангенциального разрыва СЕ, по обе стороны которой давления одинаковы, а температура и плотности различны, так как изменения энтропии при переходе через ВС и АС — CD будут различными. В области 3 за Я-образным скачком поток вихревой.
Отражение скачка, показанное на рис. 4-25,6 может возникнуть при значительных углах отклонения 8 и малых сверхзвуковых скоростях Ях. Подчеркнем, что механизм возникновения Я-образного и мостообразного скачков одинаков.
б) Отражение от свободной границы струи
Такое отражение рассмотрено на рис. 4-26. Во всех точках на границе FBE давление одинаково и равно давлению внешней среды ра. В струе это же давление имеет место только до скачка АВ. При переходе через скачок АВ давление изменяется от рх = ра до pt > ра. Следовательно, точке В свойственны одновременно два давления: ра со стороны среды и рг со стороны струи. Такая точка является очагом возмущения сверхзвукового течения, создающим стационарную волну разрежения. При обтекании точки В давление потока должно упасть от р2 до ра, что и приводит при сверхзвуковых скоростях к образованию волны BCD.
Первая характеристика BD составляет с направлением вектора М2 угол ат2 = arcsin ~, где М2 — скорость потока за скачком АВ (М2 < Mt). Угол последней характеристики ат3 arcsin Здесь скорость за отраженной
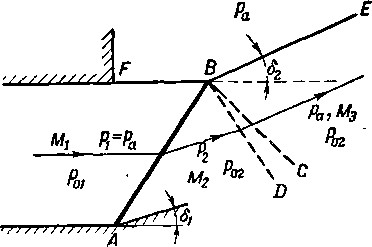
Рис. 4-26. Отражение косого скачка от свободной границы струи.
волной разрежения М3 определяется по отношению — ,
Рог
где р02— давление торможения за косым скачком.
Отражение скачка приводит к деформации границы струи, которая в точке В отклоняется на угол 82>8,.Это отклонение вызывается расширением струи. Таким образом, при отражении от свободной границы струи, вдоль которой давление сохраняется постоянным или падает, скачок уплотнения преобразуется в волну разрежения. Если давление вдоль границы возрастает, то в зависимости от интенсивности изменения давления отражение может быть погашено или оно происходит с сохранением знака (как и от твердой стенки).
4-9. ВЗАИМОДЕЙСТВИЕ СКАЧКА И ВОЛНЫ РАЗРЕЖЕНИЯ
При обтекании тел конечных размеров сверхзвуковым потоком совершенного газа интенсивность скачков на различных расстояниях от тела будет различной. Благодаря взаимодействию с волнами разрежения по мере удаления от тела интенсивность скачков уменьшается и на бесконеч? ном удалении становится бесконечно малоед.
Рассмотрим в качестве примера обтекание заостренной пластинки (рис. 4-27). На переднем остром (8<§т) носике пластинки возникает плоский косой скачок АВ. При обтекании точки D образуется стационарная волна разрежения, причем характеристика, на которой начинается отклонение потока, расположена под углом
где М2 — скорость за скачком.
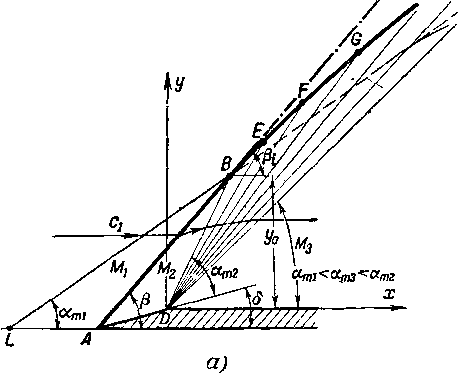
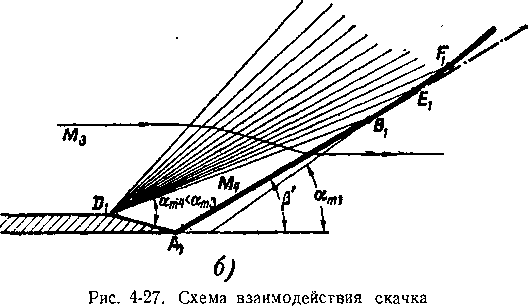
и волны разрежения.
Так как
йт2“И>Рп
то характеристика пересечет скачок уплотнения в некоторой точке В. Второй границей волны разрежения является
. 1
характеристика, расположенная под углом am3 = arcsin —.
На участке правее точки В волна разрежения взаимодействует с косым скачком. В области ABD скорость постоянна и равна Мг; линии тока параллельны образующей клина AD. Проведем через точку В характеристику невозмущенного потока под углом am] = arcsin к направлению вектора скорости сг. Так как косой скачок располагается под углом (3. (аш1 -(- ami -(- S.), а угол ближайшей к DB волны DE меньше ат2, то на участке BE косой скачок отклоняется на малый угол так, что с уменьшением угла наклона скачка (3j уменьшается и угол отклонения потока S.. Соответствующие отклонения скачка и изменения угла поворота потока 8 имеют место и на участках EF, FG и т. д.
Следовательно, скачок, начиная от точки В, искривляется и отклоняется в направлении потока; угол скачка уменьшается, приближаясь к ат1.
В соответствии с основными формулами скачка можно заключить, что при взаимодействии с волной разрежения интенсивность скачка уменьшается и, следовательно, уменьшаются потери в скачке. Изменение энтропии, как показывает анализ, становится равным нулю на бесконечности.
Аналогичные результаты получаются, если волна разрежения расположена перед скачком (рис. 4-27,6). В точке Dj возникает волна разрежения, а в точке Аг — скачок уплотнения. Взаимодействуя с волной разрежения, скачок искривляется. Так как после пересечения с последней характеристикой волны разрежения D1B1 скачок А1В1 попадает в зону меньших скоростей, угол его (3; увеличивается.
Заметим, что в реальной (вязкой) жидкости затуханию скачков способствует также внутреннее трение.
В предыдущих параграфах настоящей главы былй рассмотрены скачки уплотнения в плоском течении. При обтекании осесимметричных тел поверхности разрыва имеют осесимметричную форму.- Рассмотрим особенности осесимметричного скачка на примере обтекания кругового конуса (рис. 4-28). Перед конусом образуется конический скачок, вершина которого совпадает с вершиной конуса, если угол раствора конуса меньше максимального значения для данной скорости набегающего потока.
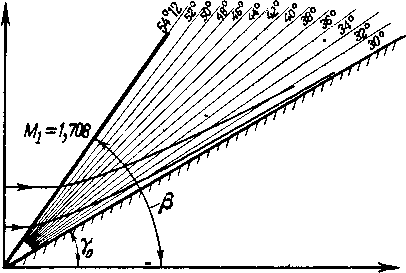
Рис. 4-28. Форма линий тока в возмущенной области за коническим скачком при обтекании конуса.
Основные соотношения при переходе через поверхность конического скачка, как легко видеть, будут теми же, что и для плоского скачка [уравнения (4-13), (4-14) и др.]. При одинаковых углах раствора клина и конуса скачок на конусе будет иметь меньший угол наклона, чем на клине, так как конус вызывает меньшие стеснения потока, чем клин бесконечного размаха того же угла раствора. При переходе через конический скачок линии тока, так же как и в случае плоского скачка, претерпевают излом. Однако так как скачок на конусе слабее, чем на клине, непосредственно за скачком линии тока будут наклонены к вектору скорости невозмущенного потока под углом, меньшим угла раствора конуса у0. Расчеты показывают, что в возмущенной области линии тока не являются пря-
мымй, кай при обтекании клина, а кривыми, прйчем кривизна их различна и зависит от расстояния от поверхности конуса. Кривизна линий тока, ближайших к поверхности конуса, весьма мала.
Из рис. 4-28 следует, что с удалением от скачка угол наклона линий тока к оси конуса увеличивается и линии тока асимптотически приближаются к направлению, заданному образующей конуса. Здесь можно видеть, что кольцевая трубка тока, образованная двумя смежными линиями тока,
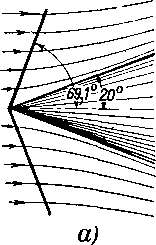
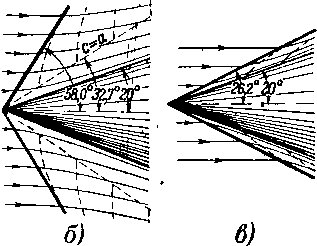
Рис 4-29 Схемы спектров обтекания конуса при различных скоростях невозмущенного потока.
имеет плавно суживающуюся форму. Линии тока обращены выпуклостью к поверхности конуса. При сверхзвуковых скоростях такая форма означает уменьшение скоростей и рост давлений вдоль линий тока, т. е. торможение потока. Отсюда следует, что за коническим скачком продолжается сжатие газа. Однако если в пределах скачка повышение давлений сопровождается ростом энтропии, то сжатие газа в возмущенной области за скачком происходит изоэн-тропическим путем, без потерь. На этом основании можно
заключить, что при одинаковом отношении давлений у
(/?а—давление на поверхности обтекаемого клина или конуса) сжатие газа при обтекании конуса происходит с меньшими потерями, чем при обтекании клина, так как для конуса полное повышение давления является суммой изоэнтропи-ческого сжатия и сжатия по ударной адиабате.
В сверхзвуковой части возмущенной области благодаря кривизне линий тока характеристики криволинейны.
На рис. 4-29 изображены три возможных случая: скорости во- всех точках возмущенной области меньше скорости звука (а), случай смешанного течения, когда скоро-рости непосредственно за скачком сверхзвуковые, а затем становятся дозвуковыми (б), и, наконец, когда поток за скачком полностью сверхзвуковой (б). Характер течения за скачком при неизменной величине у0 зависит от скорости набегающего потока.
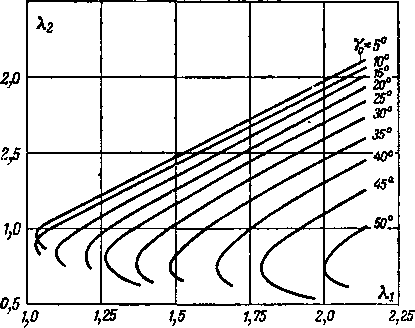
Рис 4-30. Зависимость скоростей на поверхности конуса от скорости невозмущенного потока и угла конуса
Скорости и давления на поверхности конуса меняются при изменении скорости невозмущенного потока и полуугла конуса Yo-
На рис. 4-30 приведены графики изменения безразмерной скорости на поверхности конуса Я2 в зависимости от угла Yo и Следует заметить, что при данном режиме обтекания во всех точках конической поверхности скорости и давления имеют постоянные значения. Для конуса, так же как и для клина, теоретическое решение задачи дает при одном и том же режиме два возможных значения угла наклона скачка и параметров у поверхности конуса (нижние ветви кривых на рис. 4-30). Однако практически, как правило, реализуются меньшие значения углов скачка (верхние ветви кривых на рис. 4-30). Поэтому можно сделать вывод, что с увеличением у0 скорости на поверхности конуса уменьшаются и давления растут. Увеличение скорости невозмущенного потока приводит к противоположным результатам.
Такой характер изменения параметров потока на поверхности конуса имеет место до тех пор, пока угол
конуса не достигнет предельного значения, при котором происходят отход и деформация скачка, так же как и в случае клина. При этом конический скачок преобразуется в осесимметричную поверхность разрыва с криволинейной образующей. Однако максимальные полууглы конуса Y0m; при которых для данного Я\ происходит преобразование конического скачка 6 осесимметричный с криволинейной образующей, будут больше соответствующих значений Ьт для клина. На рис. 4-31 приведены зависимости максимальных углов отклонения Ьт (и Тот 0Т числа для клина и конуса.
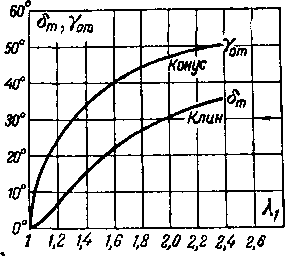
Рис. 4-31. Зависимость максимальных углов клина и конуса от скорости невозмущенного потока (ft = 1,4).
Для конического скачка можно построить в плоскости годографа и, и и в тепловой диаграмме ударную поляру (рис. 4-32).
В плоскости годографа изменение скорости непосредственно в коническом скачке изображается линией DEA, причем вектор скорости за скачком определяется отрезком ОЕ (скорость невозмущенного потока OD). Угол скачка р можно найти, проведя нормаль в точке Е к отрезку DE. Изменение скорости в возмущенной области за скачком описывается кривой ЕЕХ. Эта линия отвечает изоэнтропическому изменению скорости (сжатию) за скачком.
Яблоковидная кривая DEXA определяет годограф скорости на поверхности конуса; ее можно назвать ударной полярой конуса. Наклон отрезка OEt определяет полуугол конуса Yo- Область, заключенная между кривыми DEA и DEj^A, характеризует поток в возмущенной области. В любой точке N отрезок ON определяет величину и направление скорости. Нормаль, проведенная к годографу скорости в точке N, дает полуугол конической поверхности, проходящей через эту точку в плоскости потока.
Каждая промежуточная кривая DNAt соответствует постоянному значению разности углов 8—у Так как в возмущенной области давление полного торможения не меняется, то годографу скорости ЕЕг
отвечает постоянное значение . Нанося эти значения для различно 1
ных точек Е, можно при пользовании ударной полярой определить изменение давления торможения. В плоскости годографа можно провести дугу окружности радиусом которая выделяет группу режи-
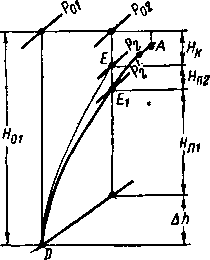
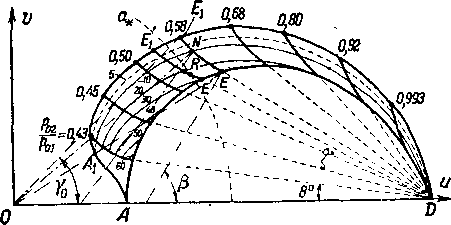
Рис. 4-32. Ударная поляра для конического скачка в плоскости годографа и в тепловой диаграмме для 6=1,4 (яблоковидные кривые).
6)
мов обтекания конуса с дозвуковыми скоростями за скачком. При этом легко устанавливаются точки возмущенного потока, в которых скорость течения равна критической. Для данного угла скачка (i эти точки получаются пересечением дуги д* с годографом скорости Е'Еу (точка К).
В тепловой диаграмме ударная поляра строится уже известным нам способом (рис. 4-32,6). Линия ПЕгА соответствует изменению состояния газа за коническом скачком при изменении р0 в пределах от я
Ро= “о (точка D) до ро = g- (прямой скачок). При определенном значении Ко и соответственно ро состояние потока непосредственно за скачком характеризуется точкой Ev определяющей изменение энтропии (потери Ah) и изменение потенциальной энергии газа в скачке (#п1).
Отрезок отвечает изоэнТропическому сжатйю за скачком, и в точке Е можно найти параметры газа на поверхности конуса. Соответствующее изменение потенциальной энергии равно Нп2- При одинаковых углах плоского и конического скачков (Р = ро) изменения параметров получаются близкими, так как изоэнтропическое сжатие в возмущенной области значительно менее интенсивно, чем ударное сжатие в скачке.
В системе конических скачков можно осуществить последовательное торможение сверхзвукового потока, так же как и в системе плоских скачков.
В заключение необходимо сделать следующее замечение.
-До сих пор мы предполагали, что любой скачок представляет собой геометрическую линию (или поверхность).
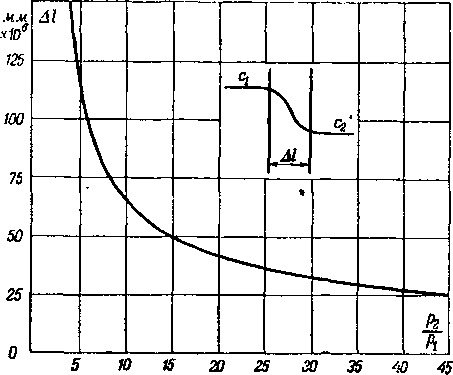
Рис. 4-33. Толщина скачка в зависимости от его интенсивности.
Это означает, что переход от параметров' невозмущенного потока к параметрам за скачком совершается в бесконечно тонком слое. Существование двух смежных областей потока с различными температурами и скоростями в реальном— вязком—газе возможно только при наличии некоторого переходного слоя конечной толщины, в пределах которого и происходит весьма интенсивное, но все же постепенное изменение параметров.
Привлекая методы кинетической теории газов и основные уравнения газодинамики с учетом теплопроводности и вязкости, можно получить приближенную оценку толщины прямого скачка.
Расчеты показывают, что толщина скачда имеет поря-1.док удвоенной длины свободного пробега молекулы и поэтому уменьшается с ростом его интенсивности. Соответствующий график изменения толщины скачка в зависимости
от — при не слишком малых давлениях представлен на
рис. 4-33. Мы видим, что толщина скачка в обычных условиях весьма мала. Опыты подтверждают, что принятая выше упрощенная схема бесконечно тонкого скачка и выведенные в этом предположении формулы в обычных условиях весьма точно отражают действительную картину. Следует иметь в виду, что в разреженных газах при больших длинах свободного пробега толщина переходной области может оказаться весьма существенной; очевидно, в этом случае полученные соотношения для скачка могут давать существенные погрешности.
4-11. СКАЧКИ КОНДЕНСАЦИИ (ТЕПЛОВЫЕ СКАЧКИ)
Скачки могут возникнуть не только в адиабатических потоках, но и в тех случаях, когда на малой длине потока происходит интенсивный подвод или отвод энергии (например, тепла). При этом образуются скачки, называемые тепловыми. Наибольший интерес представляют два вида тепловых скачков- распространение детонации и горения и скачки конденсации, связанные с движением двухфазной жидкости и, в частности, влажного пара или воздуха
Первый тип тепловых скачков подробно изучен и освещен в специальной литературе. Второй тип — скачки конденсации, широко встречающиеся в практике аэродинамического эксперимента, в соплах Лаваля, в проточных частях турбомашин, изучен менее подробно.
Анализ свойств скачков конденсации основывается на некоторых допущениях: а) конденсация происходит мгновенно, так что образуется! резкая граница, отделяющая газ с несконденсировавшимися водяными парами, от газа, содержащего конденсат; б) эффект конденсации сводится к освобождению скрытой теплоты парообразования; в) этот процесс сопровождается изменением физических свойств газовой составляющей и уменьшением ее весовой доли в смеси; изменение физических свойств газа и его параметров происходит только в пределах скачка; г) влиянием вязкости, теплопроводности, диффузии можно пре-
р
небречь; д) газовая фаза подчиняется уравнению состояния —=gRT
и k меняется только прн переходе через скачок; е) после скачка жидкая фаза имеет ту же скорость, что и газообразная.
Основными уравнениями скачка конденсации 55 являются общие уравнения, выведенные в § 4-2.
С учетом обозначений, принятых на рис. 4-34, уравнение неразрывности запишем в следующем виде:
Pic«l =.Рг(1 +/)сл2 = Рг С1 + /Нйг sin Рк— o2cos Рк), (4-37)
где рк—''угол косого скачка конденсации-
Р X
/ = —----отношение массы жидкости к массе газа за скачком:
Ра 0 — 1)
X — степень влажности за скачком; рн — плотность жидкости.
C«2=a2Sin Рк—y2COS Рк.
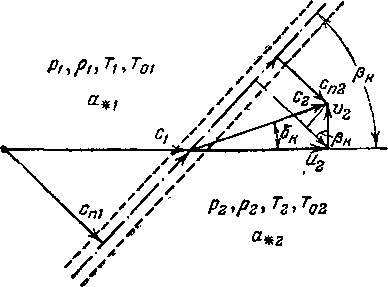
Рис. 4-34. К выводу уравнений косого скачка конденсации.
Уравнения количества движения в проекциях на нормаль к скачку и на плоскость скачка будут:
Рг — Р 1 = Pi^! — Рг (1 + /) («2 sin Рк— v2 cos Рк)56; (4-38)
?icnlct = Pzi1 i-j)cn2ct =
= Рг U + i) («2 sin PK— v2cos PK) (u2cos PK+ v2sin y=0, (4-39)
где ct= c, cos gK = m2 cos + v2 sin fK.
Уравнение энергии запишем в такой форме: с2 с2
_J_ (, = _JL /2 — Д(0, (4-40)
где Дi0 = (02 — i01 — изменение энтальпии торможения вследствие выделения теплоты при конденсации.
Так как энтальпия торможения при пересечении скачка меняется, то критические скорости до и после скачка будут неодинаковыми:
-«-К57!
+ 1 ‘°2
Здесь kv k2 — показатели изоэнтропического процесса до и после конденсационного скачка.
Соотношение между критическими скоростями выражается формулой
д2' К (4-41)
a2 = “il =
+
где
— 1 k2 +
— A i
а/0 = т^; К = г
1 •
1 +
Pi
'I
а,
Р, 2(fe, — 1)
Левую часть уравнения энергии (4-40) можно представить в следующей форме
„2
(4-40а)
+ 1 а%= (01(1 + дг0) (4-406)
а правую часть «2 + и2 ,
Рг
-1р2(1+/) 2 (*ж — 1)
Учитывая, что
(4-42)
И tg!
к и.
где 5К— угол отклонения линии тока при пересечении скачка конденсации, с помощью выражений (4-37), (4-38), (4-40), (4-41) и (4-42) получим уравнение ударной поляры для скачка конденсации в таком виде:
иа(Х, — и,)-
—2 /•> —у> ^1 М2
v2 — ( 1 й2/ 2
_J_ 1 ^1 - ^1М2 +
— (kt — 1)^2 — (fe, + 1) (1 + Д/0)
— 1
- Д(0 — k----
(4-43)
+1 - + 1
, С1 - Ц2 - V2 — ,
“2==^; *=*!-*.¦
Уравнение (4-43) при Дг0 =* Ъ = 0 переходит в формулу (4-26) для адиабатического скачка.
С помощью (4-43) по формулам (4-42) определяются угол косого скачка конденсации Рк и угол отклонения потока 8К.
Из уравнения энергии (4-406) можно получить формулу для определения числа М2 за скачком:
м| + у|
Аналогично тому, как это сделано при выводе формулы (4-35), получаем формулу для отношения давлений торможения на скачке конденсации:
kt— к
2 (Л, — 1) ' «22 + .2
Отношение давлений на скачке находим по формуле
__1 + ktM2{ sin рк_
(fe, —~k) (1 + l)Ml - „ • - ГГ
1 + --_У
¦ (“г sin
рк— v2
cos ?к)2
(1+/) = 1 + Д(0
(1 + k) (k, —
+
v:
-\-(ki i k) -
-г Mi
Af,=
1
(4-44)
¦к)
(4-45}
ft,—i-,
Рог_Рг
Pot 1*1
(4-46)
k,~i
Af?
+ (&i — ^“2”
Отношение плотностей на скачке
Ра _Рг(МЛ* h Pi Pl\Mi) й2+р2
(4-47)
Полученная система шести уравнений (4-42) — (4-47) позволяет найти параметры за скачком v2, и2, М2, р02, р2 и tg Рк при заданных
параметрах до скачка с„ />,, р„ аг1 и известных Ai0, /, k.
С помощью общих соотношений нетрудно рассмотреть отдельные частные случаи.
go многих практически важных случаях можно полагать, что физические свойства газа сохраняются неизменными (к-, = k2\ k = 0)n что масса конденсированной фазы за скачком пренебрежимо мала по сравнению с газообразной (/ = 0) В этом случае уравнение (4-43) упростится и примет вид:
^ =
(*.-«2)2-\-¦*'
-----(4-48)
?ТрГ + 1
Совместное решение исходных уравнений после соответствующих упрощений позволяет получить связь между нормальными составляющими скорости на скачке конденсации в следующей форме:
Ьг 2 =
_2 ь\ l~k + Taicos2?k
......*~ГГ»-• (4'50)
2 -=^- - г-гт х? cos2 3„
: “Ь 1
а:
Величина а, определяется по формуле (4-41) Для отношения давлений на скачке находим:
?¦» -M(k-AM2 ialt р 1 Yjl.^«l_A + i.
Это уравнение переходит в формулу (4-13J при ~b, = 1 (адиабати-
ческий скачок) после подстановки —— из уравнений (4-5) и (4-11).
сп2
Из уравнения (4-48) следует, что вертикальная составляющая скорости за скачком обращается в нуль при трех значениях вектора и2.
Первое соответствует Вырождению скайка а слабую волну [иг = = Х,(Х2 = a»Xj)]. Второе и третье значения получаются из условия
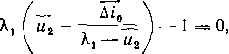
или
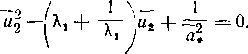
Два корня этого уравнения будут:
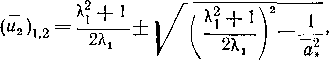
т. е.
д!(Х? + 1)2_, (4.51)
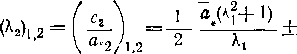
/
4Х?
Полученное соотношение выражает связь между скоростями для прямого скачка конденсации. В этоМ легко убедиться, под
тс — _
ставив в уравнение (4-49) условия прямого скачка: $к=2 и Ь* = а* .
Из уравнения (4-51) вытекает, что скорость за прямым скачком зависит от X, и Дг0 — теплоты, выделяемой при конденсации, которая в свою очередь определяется количеством конденсирующегося^газа.
Из уравнений (4-49) и (4-50) следует, что величины b* и а. не могут быть меньше некоторого предельного значения для заданного сп1 илн Х„ так как в противном случае сп2 и Х2 будут мнимыми величинами. Из (4-51) для прямого скачка
Д*мин Х2 + ! •
В согласии с формулой (4-41) при /г, = /г2 минимальному значению а, соответствует максимальное изменение энтальпии торможения в скачке:
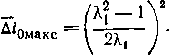
(4-52)
В общем случае для косого скачка из уравнения (4-49) получим:
соответственно из (4-50) будем иметь:
_2(4 + 1)
/ [k+l +Х2(2/г stn2 Рк + l-ft)]2
V
• 4 (*2 — 1) X, cos2
Xfsin2
(4-53)
— at
ДI
Очакс —о
at,
Как указывалось, относительное изменение энтальпии торможения в скачке конденсации Дi0 характеризует количество конденсирующейся жидкости. Полученные соотношения показывают, что скачки конденсации могут возникать только при определенных количествах конден сирующейся жидкости. Предел конденсации в скачке зависит от скорости перед скачком и от угла скачка.
Возвращаясь к анализу уравнения ударной поляры (4-48), отметим, что у2= со при
4-( —-—X? + 1 ) или -^2-=_1J —-—X'f + 1 I. X, U + 1 1 ' " I
2 >2 й*2 "Н ^
Зависимость (4-48) графически представлена на рис. 4-35 для раз личных значений а». Для плоского косого конденсационного скачка
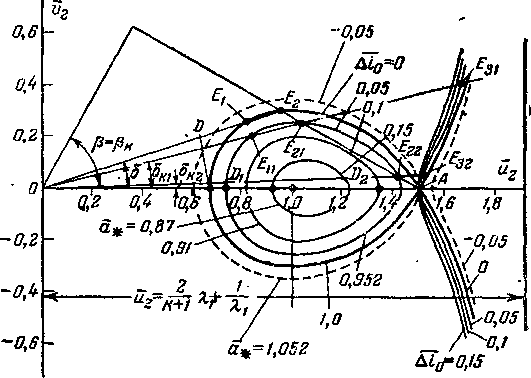
Рлс. 4-35. Ударные поляры конденсиционных скачков для различных значений Д/0 (различной относительной влажности); Х, = 1,5‘.
k= 1,4.
при данном а.(Дг0) на ударной поляре находим две точки: Е21 и ?22, отвечающие двум различным углам скачка. Причем точка Е21 соответствует криволинейному конденсационному скачку. Точки Е3 отвечают скачку разряжения.
Ударной поляре адиабатического скачка соответствует значение а, = 1. По мере уменьшения а, (увеличения Дг0) угол скачка конденсации при данном 5К возрастает. Прямому конденсационному скачку
в соответствии с формулой (4-51) отвечают два значения вектора и2 (точки D, и D2)- Отрицательный знак перед корнем в (4-51) дает точку D,, а положительный — Ог.
Таким образом, уравнения (4-43) и (4-48) и ударная поляра на рис. 4-35 показывают, что теоретически возможно существование четырех типов прямых и косых конденсационных скачков, отвечающих различным скоростям перед скачком и величинам «ДДг0).
Соответствующая классификация указана в табл. 4-2.
Таблица 4-2 Возможные типы конденсационных скачков
| Нормальная составляющая скорости перед скачком |
Отношение критических скоростей |
Нормальная составляющая скорости за скачком | Тип скачка |
| Сп1 |
1 а# ^ мин | * * сп2 аг |
Скачок разреже ния |
| 2- сп2 < «2 |
|||
| Сп1 >а1 | 1 > 51 > а# мин | 3- сп2 ^ а2 |
Скачок |
| 4. сп2 < а2 | уплотне ния |
Однако если учесть некоторые дополнительные условия, то возможными оказываются скачки всего двух типов: 1) сверхзвуковые скачки, в которых cn^>av сп2^а2 и конденсация сопровождается сжатием газа (рг /?,); 2) дозвуковые скачки, отвечающие условиям сп'2<^а* ив которых конденсация сопровождается разрежением газа (Pi<iPi). Скачки, отвечающие соотношениям сл1>д, и сп2^> д2> не могут реально осуществиться, так как такой скачок перемещался бы относительно находящегося перед ним газа со сверхзвуковой скоростью и его возникновение не должно было бы отразиться на состоянии этого газа.
Скачки конденсации в дозвуковом потоке не могут перевести газ в область сверхзвуковых скоростей сп2^ а2), так как в этом
случае необходимо отводить от газа теплоту, что не соответствует условиям конденсации.
Определим изменение энтропии в конденсационных скачках.
В частном случае k — 0 получим:
k
AS=^[(l+^0)fe-‘g-;]. (4-54)
В формулу (4-54) входит отношение которое можно найти по
Р 02
- Рг
уравнению (4-46), подставляя k = 0; прн этом М2 н — определяются
по формулам (4-44) и (4-45).
Исследуя уравнение (4-54), можно убедиться в том, что для скачков первых трех типов (табл. 4-2) As ]> 0. Однако, привлекая дополнительное условие (термодинамическое состояние перед скачком должно соответствовать началу быстрой конденсации) н учитывая влияние теплообмена, можно показать, что скачок первого типа, как и четвертого, невозможен.
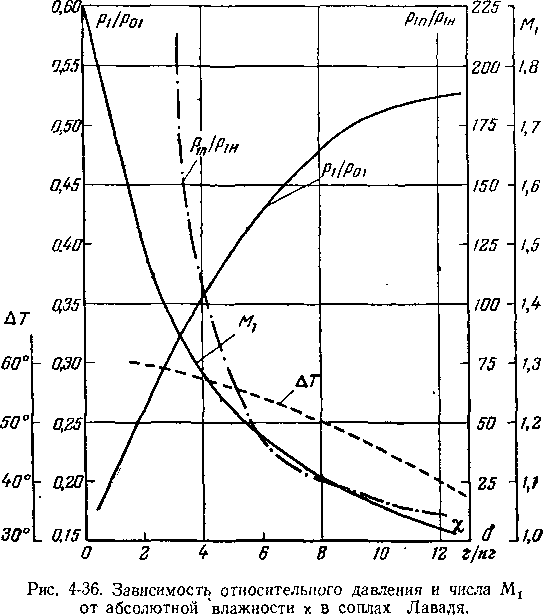
Опыт подтверждает возможность образования скачков второго и третьего типов.
На положение скачка, его форму и интенсивность решающее влияние оказывают влажность воздуха и скорость потока. На рис. 4-36 приведены кривые относительного давления и числа М, перед скачком конденсации в зависимости от абсолютной влажности воздуха х по опытам А. А. Степчкова, проведенным в соплах Лаваля. С увеличением влажности скачок конденсации перемещается в область меньших чисел Мг.
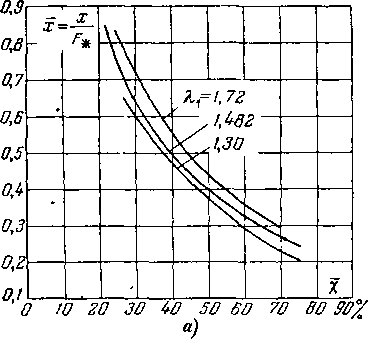
Рис. 4-37.
а —изменение положения конденсационных скачков в сопле Лаваля в зависимости от скорости и относительной влажности б—схема скачка в сопле.
б)
С увеличением влажности уменьшается пересыщение потока воздуха парами воды, определяемое- отношением парциального давления
Р\п
пара к давлению насыщения —— , а также переохлаждение Ду =
Р !н
= Га1—Г, (рис. 4-36), где jh1—температура насыщения, а Г,—температура перед скачком. По мере возрастания влажности величины пересыщения и переохлаждения уменьшаются. -
Перемещение скачка конденсации в зависимости от влажности объясняется, по-видимому, тем, что с уменьшением количества паров воды конденсация их происходит при более низкой температуре, соответствующей большому числу М,. При перемещений меняется и форма скачка: при большой влажности скачок становится мостообразным и приближается к прямому; с уменьшением влажности наблюдается, как правило, система двух пересекающихся скачков.
В заключение отметим, что изложенная теория конденсационных скачков оставляет в стороне вопросы механизма конденсации, зарождения и развития ядер конденсации.
ГЛ АВА ПЯТАЯ ДВИЖЕНИЕ ГАЗА ПРИ НАЛИЧИИ ТРЕНИЯ
5-1. ТЕМПЕРАТУРА ТОРМОЖЕНИЯ В ВЯЗКОЙ ЖИДКОСТИ
При рассмотрении движения реальной (вязкой) жидкости необходимо учитывать диссипацию (рассеяние) энергии, вызываемую внутренним трением и теплопроводностью, т. е. термодинамической необратимостью процесса.
Движение вязкой жидкости описывается системой уравнений сохранения: расхода, количества движения и энергии. Уравнение неразрывности (1-12), как уже указывалось, справедливо и для вязкой жидкости. Уравнения количества движения в форме Эйлера (1-16) должны быть дополнены членами, учитывающими влияние вязкости.
Следует подчеркнуть, что для необратимых процессов движения интегралы уравнений движения и энергии не-совпадают. При выводе уравнения энергии для струйки (§ 2-1) указывалось, что оно справедливо и для адиабатических (необратимых) течений. Однако это замечание вполне справедливо только в частном случае, когда работа сил трения полностью преобразуется в тепло. Такой процесс соответствует простейшей схеме одномерного потока или движению газа с равномерным полем скоростей.
При рассмотрении движения вязкой жидкости с неравномерным распределением скоростей в потоке условие эквивалентности теплоты трения и работы трения не выполняется. В таком потоке только часть работы трения превращается в теплоту, а другая часть вызывает чисто механический эффект: перестройку поля скоростей, в процессе которой происходит перераспределение кинетической энергии между частицами жидкости. Отсюда вытекает, что различные частицы приобретают разное количество теплоты трения и имеют разный запас полной энергии. Следовательно, условие г0 = const в общем случае не является интегралом уравнения энергии для всей массы
196
6П2.2 Дейк Михаил Ефимович
Д 27 Техническая газодинамика. Изд. 2-е, переработ. М.—Л. Госэнергоиздат, 1961
с черт. и илл. 6П2.2
design pashaok
Редактор Б. Я- Шумяцкий Техн. редактор А. М. Фридкин
ГЛ АВА ПЯТАЯ ДВИЖЕНИЕ ГАЗА ПРИ НАЛИЧИИ ТРЕНИЯ
5-1. ТЕМПЕРАТУРА ТОРМОЖЕНИЯ В ВЯЗКОЙ ЖИДКОСТИ
При рассмотрении движения реальной (вязкой) жидкости необходимо учитывать диссипацию (рассеяние) энергии, вызываемую внутренним трением и теплопроводностью, т. е. термодинамической необратимостью процесса.
Движение вязкой жидкости описывается системой уравнений сохранения: расхода, количества движения и энергии. Уравнение неразрывности (1-12), как уже указывалось, справедливо и для вязкой жидкости. Уравнения количества движения в форме Эйлера (1-16) должны быть дополнены членами, учитывающими влияние вязкости.
Следует подчеркнуть, что для необратимых процессов движения интегралы уравнений движения и энергии не-совпадают. При выводе уравнения энергии для струйки (§ 2-1) указывалось, что оно справедливо и для адиабатических (необратимых) течений. Однако это замечание вполне справедливо только в частном случае, когда работа сил трения полностью преобразуется в тепло. Такой процесс соответствует простейшей схеме одномерного потока или движению газа с равномерным полем скоростей.
При рассмотрении движения вязкой жидкости с неравномерным распределением скоростей в потоке условие эквивалентности теплоты трения н работы трения не выполняется. В таком потоке только часть работы трения превращается в теплоту, а другая часть вызывает чисто механический эффект: перестройку поля скоростей, в процессе которой происходит перераспределение кинетической энергии между частицами жидкости. Отсюда вытекает, что различные частицы приобретают разное количество теплоты трения и имеют разный запас полной энергии. Следовательно, условие г0 = const в общем случае не является интегралом уравнения энергии для всей массы жидкости, так как в потоке образуется местное перераспределение энергии.
В качестве примера рассмотрим движение вязкой сжимаемой жидкости между двумя плоскими стенками
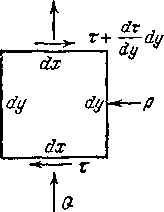
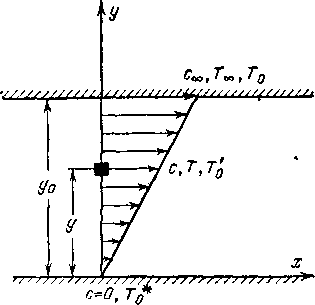
Рис. 5-1. К выводу уравнения энергии для потока сжимаемой вязкой жидкости между двумя плоскими стенками (безградиентное течение).
(рис. 5-1). Верхняя стенка движется в направлении оси х с постоянной скоростью, равной скорости газа с . На нижней стенке скорость равна нулю, так как эта стенка неподвижна58. Полагаем, что давление сохраняется постоянным вдоль осей х и у, т. е.
=др_ __п дх ду
Если скорость движения верхней стенки мала, для адиабатического потока можно считать, что температура постоянна и одинакова для всех точек потока. Если же величина с достаточно велика, то необходимо учитывать, что температура Т является функцией у. В таком течении эффект сжимаемости проявляется только в связи с изменением температуры газа; плотность газз меняется в соответствии с формулой (для идеального газа)
, ^_ р const
Так как в рассматриваемой задаче скорости по оси л: не меняются, а давление сохраняется постоянным как по у, так и по х, то закон сохранения энергии формулируется весьма просто: количество теплоты, подведенное
к элементу, плюс работа сил трения равны нулю.
Обозначим: Q—’Количество тепла, переданное элементу в единицу времени от соседних частиц; т — напряжение трения. Количество тепла, полученное элементом, определяется как разность (рис. 5-1):
Qdx — (Q-\-^dyjdx = ~^ dydx*-
Разность секундных работ сил трения находим по уравнению
Тогда уравнение энергии будет:
[(х+|^) [c + 7idy)
нергии
¦(-Q + w) = o,
dx (тс) dydx.
d dy или
— Q-\-zc = const.
Постоянная в правой части уравнения энергии опреде^ ляется из граничных условий. Так, при у = 0, с = 0 и Q = Q0, где Q0 —удельное количество тепла, передаваемое потоку газа от внешнего источника.
Следовательно,
— Q-\-vc = — Q0.
Для ламинарного движения г определяется по формуле (1-4). Вспомним, что
г)__2 ^
где Я — коэффициент теплопроводности.
После несложных преобразований получаем: л dT. dc d (срт , с2 Л ^
1 df +^ df — 57VTT+T')= ~ Qo'
![]()
называют числом Прандтля. Отметим, что входящие в выражение для Рг коэффициенты теплопроводности и вязкости зависят от температуры:
Величину
i = l(T) и |* = [i(7’).
Интеграл уравнения энергии для случая = const позволяет связать статическую энтальпию в потоке с энтальпией у неподвижной стенки следующим образом:
У
![]()
о
и
У
![]()
о
о
где при линеином распределении скоросп
т0—напряжение трения на стенке; г* = с Т0 — энтальпия торможения на стенке.
Следовательно,
;-/; + Рг^=-Рг^. (5-1)
Для верхней стенки, движущейся вместе с потоком со скоростью сто, нетрудно получить:
![]()
(5-1а)
С помощью (5-1) и (5-1а) после несложных преобразований находим:
Найдем для случая адиабатического течения (Q^^O) отношение температур торможения на движущейся стенке и в произвольном сечении потока (на расстоянии у), учитывая, что температура торможения и термодинамическая температура связаны соотношением
![]()
(5-1 г)
Имея в виду, что рассматривается случай с = const, следовательно i — с Т, а для адиабатического течения и Qo = 0, нз (5-1) и (5-1г) получим:
![]()
Для движущейся стенки с помощью уравнений (5-1а) и (5-1 г) будем иметь:
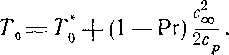
Следовательно,
Y~— 1 — 0 — Рг)
1 О
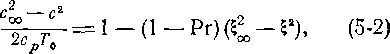
где
![]()
Формула (5-2) показывает, что для Рг ф 1 в вязком газе температура торможения, т. е. полная энергия не сохраняется постоянной по сечению. При Рг = 1 температура торможения Т'0 = Т0 = const для всех точек потока.
Число Рг характеризует соотношение между теплом, выделившимся вследствие трения, и теплом, отведенным от элемента теплопроводностью. При Рг<1, что имеет место для всех газов, отвод тепла совершается более интенсивно, чем его выделение. В этом случае Т*0 <С.Т0. При Рг > 1 выделение теплоты трения происходит более интенсивно, чем ее отвод, и Т’0^>Т0.
Для совершенного газа число Рг является физической константой, не зависимой от состояния газа.
Для более общего случая плоского потока газа, когда скорости зависят от дг н у, дифференциальное уравнение энергии может быть представлено в таком виде59:
№ (д2Г (! +Рг т М2) д2Т(1 +Рг т М2)^1 _
дТ {1+^^-М2)
= “ Тх +у ду • (5'3)
Уравнения количествS движения с добавлением членов, учитывающих влияние вязкости (уравнения Навье — Стокса), записываются в следующей форме:
ди ди ди 1 др Г [д2и д2и\ ,
ЪГ+ид7 + vdy v [ (^^ + ^2J +
1 д /ди dv '
/ d2v d2v\ 1 d (du [ dv \~| \d^+di2) )\-
+ v
Эти уравнения дополняются уравнением неразрывности (1-12) для плоского потока:
дР . д (рц) д(ру) dt dx ду
= 0; (5-4 а)
уравнением состояния (1-1) и уравнением тренчя, например для ламинарного течения законом Ньютона (1-4).
При исследовании движения газа в трубах и каналах с учетом вязкости, а также при изучении обтекания тел газовым потоком задача сводится к определению потерь энергии и аэродинамических сил, действующих на обтекаемую поверхность С этой целью необходимо решить совместно замкнутую систему шести уравнений (5-3), (5-4), (5-4а), (1-1), (1-4), определяя неизвестные функции координат: р, р, и, v, Т ит (для установившегося потока).
В связи с весьма большими трудностями решения системы уравнений движения в общем случае (такие решения удается получить только для простейших частных случаев) в практике коэффициенты сопротивления и коэффициенты потерь энергии часто определяются экспериментально путем испытания моделей в лабораторных условиях. При этом необходимо соблюдать такие условия испытания моделей, которые обеспечивают надежность получаемых результатов и позволяют распространить эти результаты на натурные объекты.
I
II
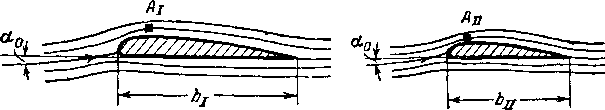
Рис. 5-2. Схема подобных потоков*
Широко применяемый в механике метод подобия позволяет сформулировать указанные условия модельных испытаний и устанавливает приемы переноса результатов лабораторных исследований на натурные объекты.
Аэродинамические силы, действующие на обтекаемое тело или на стенки канала (в том числе и силы сопротивления), выражаются через безразмерные коэффициенты. Установим, от каких параметров в общем случае зависят коэффициенты сопротивления.
С этой целью рассмотрим обтекание жидкостью двух геометрически подобных тел (рис. 5-2).
В случае кинематического и динамического подобия двух рассматриваемых явлений поля скоростей и сил в двух потоках должны быть взаимно пропорциональными. Тогда, вводя масштабы длин L, времени Т и массы М, можно представить связь между длинами, временами и массами двух подобных потоков следующим образом: V = Ы; t' = Tt; m.'= Mm.
Масштабы всех других величин, входящих в уравнения (5-4), легко выражаются с помощью указанных масштабов.
Допустим, что уравнения (5-4) выражают связь между параметрами течения первого потока. Имея в виду размерности величин, входящих в эти уравнения, отраженные в единицах измерения: длины л:, у[м], скорости и, v[M/ceK], плотности р[кг-сек2/м*], кинематической вязкости v [м2/сек}, массы т[кг- сек2/м) и давления р [кГ/м2], легко связать параметры первого и второго потоков с помощью масштабных коэффициентов:
х __j ¦ ь _JL_ и _ v _L
х' ~~уг ’ с ~сг~~йГ~~1Г Т~’
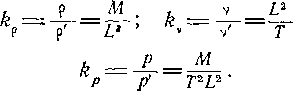
Здесь и выше штрихом обозначены параметры течения второго потока. Соотношения между параметрами (5-5) являются очевидным следствием пропорциональности линейных размеров, времен и масс двух подобных потоков.
Располагая оси координат в обоих потоках одинаковым образом, путем подстановки соотношений (5-5) в первое уравнение (5-4) можно записать для второго потока:
Уравнение (5-6) выражает уравнение количества движения в дифференциальной форме для второго потока, записанное через параметры первого потока.
Все члены уравнений (5-4) и (5-6) имеют, естественно,
одинаковую размерность [м/сек2], в чем легко убедиться с помощью соотношений (5-5). Чтобы потоки были динамически подобными, необходимо, чтобы они удовлетворяли одним и тем же дифференциальным уравнениям движения. Отсюда следует, что комплексные множители перед членами уравнения (5-6) одинаковы, т. е.
|
4 | К | — Д/[— kP |
Kkc |
| L | т |
kfL | ' L2 ’ |
|
L -1 |
ML | — 1- kp — | 1 ’ — |
| bj |
' ч |
Lk, |
Заменяя здесь масштабные коэффициенты из (5-5), окончательно получаем с учетом уравнения энергии (5-3) следующие условия подобия:
1с 1'сct_c't', gl _,gl'.
"n T’ 1 T’ ~c*~ c71’
p _ p' V-Cp_Iх-'с p
(5-7)
X' •
Таким образом, два потока являются динамически подобными, если выполняются соотношения (5-7) между параметрами этих потоков. Соотношения (5-7) называются критериями подобия. Первое соотношение (5-7) устанавливает равенство, чисел Рейнольдса в двух потоках:
Re = ^- = Re'.
Критерий Рейнольдса выражает соотношение между силами вязкости и силами инерции в потоке.
Второе условие является единственным, куда входят сходственные отрезки времени t и f, и оно получилось как следствие подобия членов, содержащих локальные уско
![]()
рения в уравнениях движения. Локальные
ускорения характеризуют только неустановившиеся, в том числе и периодические, процессы движения газа. Следовательно, второе равенство является условием подобия для неустановившихся потоков.
Отношение
Sh = ~ Sh'
носит название числа Струхаля; для периодического движения
![]()
где n — —t--частота периодически нестационарного про-
цесса.
Третье уравнение дает равенство критериев подобия, учитывающих влияние массовых- сил в потоке. Если ускорение в поле земного притяжения можно считать постоянным (g = g')> то этот критерий, называемый критерием Фруда, легко представить в таком виде:
Fr=-i- = JV-
с2
В газовых потоках влияние массовых сил, как правило, невелико и поэтому критерий Fr при моделировании газовых потоков не принимается во внимание.
Четвертое уравнение (5-5) выражает связь между статическими давлениями и скоростными напорами в сходственных точках подобных потоков. Величину
— 2р —
Р = -^=Р
можно рассматривать как характеристику, учитывающую влияние сжимаемости. В этом легко убедиться, заменяя р через скорость звука:
Тогда для двух потоков получаем:
![]()
![]()
или
Ш2 = &'М'2.
Следовательно, одинаковость чисел р имеет своим следствием равенство чисел kM, в сходственных точках потоков. Отсюда следует, что число М, известное нам из предыдущего, выступает как критерий подобия, отражающий свойства сжимаемости. В такой же мере и показатель изоэнтропы к в совершенном газе следует рассматривать как критерий подобия.
Рассматривая дифференциальное уравнение энергии (5-3) для сжимаемой вязкой жидкости, можно получить дополнительный, уже знакомый из предыдущего критерий подобия Прандтля:
![]()
Из этого же уравнения вытекает также одинаковость кри териев k и М для газовых потоков.
При турбулентном течении вводится важная характеристика — степень турбулентности:
?= —
Q 62
ьт
I
гдес63 = -д^ (с — ст)2 dt — средняя квадратичная скорость
пульсации; с — мгновенное значение скорости; см — сред-няя скорость турбулентного течения:
Cm=-^r\Cdt-
U
Резюмируя, отметим, что необходимые условия подобия двух потоков сводятся к равенству определяющих критериев в сходственных точках натуры и моделей и тождественности начальных и граничных условий.
Анализ уравнений движения и размерностей величин, определяющих сопротивление обтекаемого тела или потери энергии в потоке газа, показал, что соответствующие безразмерные характеристики сопротивления являются функциями основных критериев подобия1:
^ = ^(ИеЛМ, Рг, Sh, Е);
C = C(Re, М, Рг, Sh, Е), (5-7а)
где с —коэффициент сопротивления (см. § 5-13);
С — коэффициент потерь энергии (см. §§ 4-5; 5-14;
8-5 и др.).
При исследовании различных явлений не все критерии имеют одинаковое физическое значение. В зависимости от конкретной задачи один или несколько критериев могут иметь преобладающее значение, в то время как другая группа критериев не оказывает заметного влияния на характеристики движения.
Так, например, для установившегося движения несжимаемой жидкости критерии М и Sh теряют смысл и зависимость (5-7а) упрощается.
С учетом сжимаемости при установившемся движении для газов с одинаковыми физическими свойствами сх — = с, (Re, М).
Обеспечить равенство всех критериев подобия возможно только в натурном эксперименте, который связан с большими трудностями.
Обычно осуществляется приближенное подобие (частичное моделирование) по одному или двум наиболее важным критериям. Результаты эксперимента нетрудно скорректировать и на другие критерии, если известны значения этих критериев в опыте и зависимость изучаемых характеристик от этих критериев.
При исследовании потоков, в которых определяющими являются два или три критерия (например, Re и М или Re, М и Sh), необходимо осуществлять принципы раздельного моделирования, т. е. обеспечивать возможность независимого изменения каждого из критериев в определенном диапазоне его значений.
В заключение отметим, что рассмотренный выше прием анализа размерностей может оказаться. весьма эффективным, если известны физические параметры, определяющие исследуемый процесс, но не удается решить или даже записать систему дифференциальных уравнений задачи.
В этих случаях метод размерностей в сочетании с экспериментальными данными позволяет получить решение для целого класса механически подобных явлений.
\
5-3. ОДНОМЕРНОЕ ТЕЧЕНИЕ ГАЗА ПРИЛАЛИЧИИ ТРЕНИЯ.
ОСНОВНЫЕ УРАВНЕНИЯ
Основными уравнениями установившегося адиабатического движения вязкого газа являются уже известные нам уравнения неразрывности, количества движения и энергии.
Уравнение импульсов одномерного установившегося потока без энергетического обмена с внешней средой при наличии трения можно записать в таком виде:
cdc+d-f- + dXTp = 0, (5-8)
где dXr —единичный импульс сил трения.
Величина dXjp может быть выражена по гидравлической формуле: где С — коэффициент сопротивления; D — внутренний диа-метр трубы.
Решая совместно уравнения (5-8), (5-9), (2-14) и (2-6), можно получить дифференциальное уравнение распределения скоростей вдоль трубы переменного сечения с учетом влияния вязкости. Очевидно, что это уравнение аналогично (2-29), но должно содержать еще один член, учитывающий влияние вязкости. Простые выкладки приводят к такому выражению:
где
Формулу, определяющую изменение давления потока вдоль трубки переменного сечения, следуя уже известному методу, изложенному'в гл. 2, можно получить в следующем виде:
dp 2k h? [dF * + ! r 1 /к 11\
Из уравнений (5-10) и (5-11) можно заключить, что изменение параметров течения в трубкб^переменного сечения происходит под воздействием двух факторов: деформации потока (изменение сечения трубки) и сил трения. Уравнения показывают, что влияние трения всегда является односторонним. Так, например, при дозвуковых скоростях (1< 1) в суживающейся трубке (dF <^0) трение способствует ускорению течения (dl^>0 и dp<C_ 0). При сверхзвуковых скоростях в такой же трубке (dF< 0) трение приводит к замедленному падению скорости и соответственно к более медленному возрастанию давления по сравнению с идеальным процессом без потерь.
Из уравнений (5-10) и (5-11) следует, что в простейшем случае трубки постоянного сечения (dF — 0) при Я<1
имеем ^->0 и^-<0 и, следовательно, поток ускоряется. Нетрудно видеть, что в этом случае при сверхзвуковой скорости (Я^>1)^-<;0: поток тормозится.
Сопоставляя влияние изменения сечения трубки (деформации трубки тока) и влияние трения, можно заключить, что в дозвуковом и сверхзвуковом потоках трение приводит с качественной стороны к такому же изменению скорости течения, как и уменьшение сечения трубки.
Следовательно, воздействие сил трения в потоке можно заменить эквивалентной деформацией струи — уменьшением ее сечения в направлении движения.
Правомочность такой замены вытекает из следующих рассуждений. Движение газа в трубе без энергетического обмена, но при наличии сил трения является необратимым адиабатическим процессом. Такой процесс, как нам уже известно, сопровождается ростом энтропии. Приращение энтропии можно выразить по уравнению (4-27).
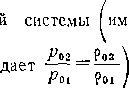
получим:
Для энергетически изолированно] ея в виду, что
7’oi = 7'o2 и что уравнение состояния
![]()
(5-12)
Так как энтропия в направлении потока возрастает, давление торможения /?02 должно уменьшаться.
По уравнению неразрывности (2-41) для двух сечений трубы заметим, что при одинаковых в обоих случаях величинах Fv А, и Л2 сечение F2 при наличии сил трения должно быть больше, чем для изоэнтропического потока.
Величину s0F можно рассматривать как живое сечение струи. Для трубы постоянного сечения (F — const) очевидно, что живое сеченне eaF при наличии трения уменьшается, так как уменьшается величина е0.
Уравнение (5-10) может быть использовано для некоторых заключений о положении сечения, отвечающего экстремальным значениям скорости. Выразим из уравнения (5-10) Логарифмическую производную сечения:
dF
![]()
F
отсюда следует, что при dX = 0 и X ф-1
k
Следовательно, сечение, соответствующее максимальной скорости при 1<1 и минимальной скорости при X >• 1, не совпадает с минимальным сечением, а смешается в расширяющуюся часть трубки. Соответственно критическим условиям (Я=1) также отвечает сечение в расходящейся части трубки. Это означает, что минимальное и критическое сечения трубки при наличии трения не совпадают. В этом случае, полагая в (5-10) 1 = 1, получим:
dF ft
5-4. ДВИЖЕНИЕ ГАЗА В ЦИЛИНДРИЧЕСКОЙ ТРУБЕ
, Из уравнения (5-10) для цилиндрической трубы (^-у = oj получим:
Из предыдущих рассуждений, а также непосредственно из анализа уравнения (5-14) легко прийти к выводу, что критическая скорость течения может возникнуть только в выходном сечении цилиндрической трубы. Действительно, согласно уравнению (5-14) при Х<^1 и dX^> 0 поток в трубе ускоряется, а при X > 1 и dX <f 0 он замедляется. Случай X = 1 в промежуточном сечении трубы противоречит уравнению (5-14) и физически нереален.
Допустим, что коэффициент сопротивления является величиной постоянной64. Тогда уравнение (5-14) можно проинтегрировать.
Интеграл уравнения (5-14) запишем в такой форме:
1 1 1 *-65 2ft , х2 К2 ^2 А + 1 ’
где Хг — безразмерная скорость в начальном сечении трубы;
X — безразмерная скорость в некотором сечении на расстоянии х от начального.
Введем безразмерную координату, которую называют приведенной длиной трубы:
2й
k+ 1
Тогда уравнение (5-14а) можно записать так:
X2
1
X*
— In
/ =
(5-15)
Зависимость между Я и % при постоянном значении Я1 ¦приведена на рис. 5-3. Величина % имеет максимум при Я = Я2 = 1.
Максимальное значение приведенной длины трубы выражается формулой
= * _1+1ПЯ?.
(5-16)
Кривые х(Я) состоят из двух ветвей, отвечающих дозвуковому (Я<^1) и сверхзвуковому (Я^>1) потокам в трубе постоянного сечения (рис. 5-3).
Кривые наглядно иллюстрируют невозможность перехода в цилиндрической трубе из одной области скоростей
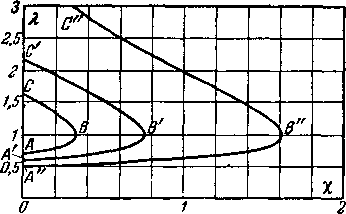
Рис. 5-3. Зависимость безразмерной скорости на выходе из трубы от скорости на входе и приведенной длины трубы.
в другую. В такой трубе, как было показано выше, при определенной скорости на входе Я1 и соответствующей длине на выходе достигается критическая скорость (Я2=1).
Дозвуковым потокам на входе в трубу (Я, < 1) отвечает участок кривой АВ (рис. 5-3)А а сверхзвуковым (Яж>1) — участок СВ. Точка В определяет максимальную величину функции % для данного значения Я1# входе в трубу, а верхняя — сверхзвуковым.
Таким образом, уравнение (5-16)' показывает, что для цилиндрической трубы заданных размеров I и D при скорости на выходе из трубы Яа = 1 и для определенных значений k и С безразмерная скорость на входе в трубу Я15 а вместе с тем и приведенный расход газа qx имеют строго определенные значения.
Из формулы (5-16) сЛедует, что при ^=1 умакс = 0. Графически зависимость (5-16) представлена на рис. 5-4. Кривая также имеет две ветви. Нижняя ветвь о.твечает дозвуковым скоростям на
3 2Л 2 1,5 1
| >1/ | { |
||||||||
| / | |||||||||
| / | |||||||||
| f | |||||||||
| 4 | |||||||||
|
XJ, | axe |
10
Рис. 5-4. Максимальная приведенная длина трубы в зависимости от скорости на входе.
в
При дозвуковой скорости на входе в цилиндрическую трубу длиной I, характеризуемую коэффициентом сопротивления С, при установившемся движении может пройти максимальное количество газа, если 12 = \.
Абсолютный расход газа через трубу предельной длины будет равен:
<Wc = &F = §F(f, «акср, А =
Вспоминая, что
1
k—I
V
2k -k + l^o —
Р А = Р.
k +1
(k + \)R У r01
у
1
k— 1
Poi_
Vt7'
(5-17)
V HI 1 макс/
получим:
G =F V~^k
макс f
(k + \)R 1 макс
Таким образом, для увеличения абсолютного расхода газа через цилиндрическую трубу определенных размеров необходимо увеличивать давление полного торможения на входе в трубу или — при постоянном значении р01 — уменьшать температуру торможения Т0. При этом в выходном сечении трубы будет по-прежнему критическая скорость, абсолютное значение которой уменьшается по мере снижения температуры торможения. Однако расход будет увеличиваться за счет увеличения плотности.
При сверхзвуковых скоростях на входе в трубу, как показывает опыт, обнаруживаются некоторые новые свойства потока, которые не описываются уравнением (5-15). Заметим, что согласно уравнению (5-15) при ^ > 1 скорость в трубе должна непрерывно падать к выходному сечению по кривой СВ на рис. 5-3, а давление — соответственно непрерывно возрастать. Однако в действительности изменение скоростей и давлений в трубе в ряде случаев происходит скачкообразно.
Прежде чем подробнее разобрать этот случай движения газа, найдем зависимости, определяющие изменение параметров потока между двумя произвольными сечениями.
Так как в изолированной трубе г0 = const, то для любых двух сечений можно написать Т01 = Т02 = const. Из этого услсвия получаем уравнение для TjTa в форме уравнения (2-22).
Для отношений давлений можно воспользоваться формулами (2-41 а) и (2-42). После несложных преобразований получим связь между статическим и полным давлениями в следующем виде:
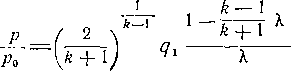
(5-18)
Отсюда при X = Я2 = 1 определяется критическое отношение давлений:
k
![]()
(5-19)
Формула (5-19) показывает, что критическое отношение
давлений — для необратимых течений будет меньше, чем
= / 2
k +1
ft—1
Уравнения (5-18) и (5-15) позволяют построить графики изменения давлений вдоль трубы для заданных значений ?i и X-
Подобный график приведен на рис. 5-5 для случая сверхзвуковой скорости на входе в трубу ^ = 1,76 и qx= = 0,453. Здесь кривая АВ характеризует повышение давления в трубе до критического значения в точке В, равного:
s'= 0,528-0,453 = 0,239.
*
Если известно распределение скоростей по трубе, а оно легко подсчитывается по уравнению (5-14а), то молено по формулам (4-20) и (4-24) определить скорости и давления за прямым скачком уплотнения в каждом данном сечении (линия СВ).
За прямым скачком поток — дозвуковой и, следовательно, давление в нем под влиянием сил трения должно падать. Так, если прямой скачок возникает непосредственно во входном сечении, то дальнейшее изменение давления протекает по кривой CD. Характер изменения давлений в дозвуковом участке трубы при различных промежу-
0,2
0.1
ОА
0.3
| А | |||
| ~н ' |
|||
| S | |||
| . | у в о ы ^ | ||
| 1 | |||
| Г | ? | ||
| -1— . 11_ |
X , . 1_1_1_1 1 | ||
0.1 02 0,3 ОА 0.5 0,6 0,7 Ofi
Рис. 5-5. Распределение давлений по трубе постоянного сечения.
точных положениях скачка представлен соответственно кривыми FM, HN и т. д. Диаграмма давлений позволяет проанализировать различные режимы течения в трубе.
При указанной скорости на входе 1г и приведенном расходе газа qx режимы в трубе без скачков возможны в тех случаях, когда у < Умакс> причем максимальное значение приведенной длины отвечает точке В. При условии макс скачки в трубе возникают только тогда, когда давление на выходе из трубы больше соответствующего давления, показываемого кривой АВ.
Допустим, что труба имеет длину, определяемую точкой / (х = 0,35), а давление за выходным сечением задано точкой L, которая лежит на кривой СВ. В этом случае прямой скачок располагается в выходном сечении трубы IL. Если давление среды, куда вытекает газ из трубы, определяется точкой К, то прямой скачок перемещается внутрь трубы и располагается в сечении EF, причем отрезок FK соответствует понижению давления в дозвуковом участке трубы. Последующее повышение давления среды приводит к дальнейшему перемещению скачка внутрь трубы (к входному сечению).
Если давление среды определяется точкой S, то в трубе скачков не возникает, а в струе, выходящей из трубы, образуется конический скачок (или система плоских косых скачков, если труба прямоугольного сечения). При уменьшении давления до величины давления в точке / интенсивность конического скачка уменьшается. В точке / конический скачок вырождается в слабую коническую волну, при пересечении которой энтропия не меняется66.
Если, наконец, давление среды меньше, чем давление в точке /, то за выходным сечением образуется коническая стационарная волна разрежения и поток газа расширяется за пределами трубы.
Кривые давлений в трубе (рис. 5-5) показывают, что при постоянной длине у и давлении на выходе рг с увеличением скорости на входе прямой скачок смещается к выходному сечению. При увеличении сопротивления трубы (путем, например, подключения дополнительного участка трубы) перемещение скачка происходит в обратном направлении (ко входу в трубу).
5-5. ПОТЕРИ НА ТРЕНИЕ В ЦИЛИНДРИЧЕСКОЙ ТРУБЕ (ОПЫТНЫЕ ДАННЫЕ)
Выше рассматривалось движение вязкого газа в трубе в предположении, что коэффициент сопротивления ? постоянен.
В действительности коэффициент сопротивления зависит от числа Рейнольдса и—в общем случае — от безразмерной скорости М. Такая зависимость устанавливается экспериментально.
Число Рейнольдса для произвольного сечения цилиндрической трубы определяется по формуле
Re =???-. г-
Для цилиндрической трубы
1
/ 2 \ 1 / 2k Pc==P1ci=^1PMa, — 4i V F+T^oiPoi’
следовательно,
Из формулы (5-20) видно, что число Re меняется вдоль трубы только вследствие изменения коэффициента вязкости (а, который зависит от температуры. Можно показать, однако, что в теплоизолированной трубе изменения температуры невелики. Так, при изменении скорости водяного пара в трубе от ^ = 0,2 доЯ2 = 1 температура изменяется на И°/о> в то время как давление уменьшается в 4,5 раза, а плотность — в 5 раз.
Изменение коэффициента вязкости воздуха в зависимости от температуры можно оценить по приближенной формуле
(этз) ’ (5-21)
где а — постоянная величина; р0 — коэффициент вязкости при температуре Т — 273°.
По опытным данным для воздуха
ц-10е = 1,757-f 0,00483*° С.
Основная задача опытного исследования адиабатических потоков газа в трубах сводится к определению коэффициентов сопротивления С и, следовательно, к нахождению потерь энергии. Методика опытного определения местных значений коэффициентов сопротивления в различных сечениях трубы основывается на уравнении (5-8), которое после
деления всех членов на а2 принимает вид;
(5-22)
Замечая, что для цилиндрической трубы произведение
Vlal=q?al = qet крй
является постоянной величиной, имея в, виду (2-46), запишем уравнение (5-22) в такой форме:
dl -J- die -J- ? ~dx = 0.
Здесь функция и зависит только от X по формуле
(2-46a).
После подстановки этой функции получим:
![]()
^ "“Ь ? ~2~dx = 0.
Отсюда можно выразить коэффициент сопротивления:
![]()
(5-23)
Уравнение (5-23) является исходным для экспериментального определения местных значений С. Перейдя в этом уравнении к конечным разностям, будем иметь:
![]()
(5-24)
Если известны расход газа G, температура торможения Т0 и распределение давлений вдоль трубы [р = р (х)], то по формуле (5-24) можно найти средний коэффициент сопротивления для некоторого небольшого участка трубы длиной Ах. Если участки Ах выбираются небольшими, то определенное таким путем значение С не сильно отличается от его местного значения.
Для нахождения связи между р и Я можно воспользоваться формулой (5-18).
Заменив здесь из уравнения неразрывности величину д, получим:
(5-25)
Рассмотрим вначале некоторые результаты опытного исследования потоков в цилиндрических трубах при небольших скоростях.
На рис. 5-6 показано изменение профиля скоростей в трубе в зависимости от числа Re для турбулентного режима. Здесь же нанесена эпюра скоростей для ламинарного потока в трубе. Сравнение кривых показывает, что профиль скоростей при турбулентном режиме значительно более „полный”, чем при ламинарном, причем с ростом числа Re наполнение профиля увеличивается.
'Рис. 5-6. Распределение скоростей при ламинарном и турбулентном режимах в трубе.
Как известно, при турбулентном двил ении, возникающем в трубах при Re > 3 ООО, имеют место перемещения макрочастиц67 в поперечном направлении. При этом частицы внешнего потока, обладающие большой кинетической энергией, перемещаясь к поверхности, увеличивают кинетическую энергию частиц у стенки, движущихся с малыми скоростями, и наоборот, частицы, переместившиеся '-от стенки в ядро потока, тормозят здесь движение жидкости.
В соответствии с изменением профиля скорости в зависимости от числа Re коэффициент сопротивления трубы должен также меняться в функции этого параметра.
Для оценки коэффициента сопротивления цилиндрических труб при небольших скоростях можно пользоваться кривыми Всесоюзного теплотехнического института, построенными Г. А. Муриным (рис. 5-7). Здесь коэффициент С представлен в зависимости от числа Re и величины, обратно пропорциональной относительной шероховатости Djk9, где k3 — средняя высота бугорков шероховатости. Заметим, что при больших значениях Djk3 (малая шероховатость) значения С по кривым ВТИ удовлетворительно совпадают с формулой Никурадзе:
^ = ~0,8 + 21g(Re]/g. (5-26)
Кривые ВТИ и формула (5-26) отчетливо показывают, что влияние числа Рейнольдса на коэффициент сопротивления в гладкой трубе простирается до весьма больших значений Re 5= 10е. По мере увеличения шероховатости влияние Re (при Re 2 -105) на увеличение шероховатости ослабевает. На рис. 5-7 пунктирной линией соединены точки, соответствующие тем значениям Re, выше которых влияние этого параметра практически не обнаруживается. Справа от этой линии расположена область, которую принято называть автомодельной68.
Перейдем теперь к рассмотрению влияния второго основного критерия подобия — числа М — на коэффициент сопротивления в трубах. Соответствующие опытные данные
Рис. 5-7. Зависимость коэффициента сопротивления S стальных труб от числа Re и относительной шероховатости по данным ВТИ.
получены в МО ЦКТИ\ в МЭИ69 и ряде других организаций.
На рис. 5-8 показано распределение статических давлений по длине гладкой трубы при дозвуковых скоростях, отвечающее различным числам Ret и на входе в трубу. В соответствии с методикой проведения опытов кривые на рис. 5-8 показывают совместное влияние числа Rej и отношения давлений (числа М,), так как раздельное моделирование по Re и М не осуществлялось. По мере снижения s
Рис. 5-8. Распределение давлений, температур и скоростей по длине трубы для дозвуковых скоростей.
(увеличения ReJ характер кривых давлений меняется и особенно интенсивно на выходном участке (х > 60 -н 70). Переход к большим значениям Re и Мг сопровождается увеличением градиентов давления: наклон линий р возрастает. Для группы режимов, отвечающих сверхкритиче-скому перепаду давлений в трубе, статическое давление в выходном сечении превышает давление внешней среды, но оказывается ниже той величины s' , которая, соответ-
*
ствует критическому истечению. Значение г можно найтц по формулам (5-19) или (5-25), подставив 1= 1.
Величина г отмечена на рис. 5-8 пунктиром. Отсюда следует, что критическое сечение не совпадает с выходным
сечением трубы и располагается внутри на некотором небольшом расстоянии от выходного сечения. С увеличением перепада давлений критическое сечение смещается навстречу потоку.
Специальные исследования выходного участка за критическим сечением показывают, что в этой области поток обладает сверхзвуковыми скоростями. Результаты исследо-
|
К—Р* |
Граница пограничного слоя
Рис. 5-9 Изменение статических давлений и скоростей по диаметру трубы вблизи выходного сечения.
вания поля скоростей и давлений на выходном участке приведены на рис. 5-9. Здесь отчетливо видна неравномерность в распределении статических давлений по диаметру трубы, причем давление на оси во всех сечениях за критическим выше, чем у стенки.
. Эпюры скоростей -(рис. 5-9) позволяют заключить, что толщина дозвукового пристеночного слоя на выходном участке уменьшается в направлении потока. Можно предполагать, что такая структура потока объясняется взаимодействием вытекающей струи с внешней средой. Благодаря интенсивному отсосу пристеночного слоя во внешнюю среду происходит его утонение на выходном участке (рис. 5-9). При этом в ядре потока создаются условия, необходимые для перехода к сверхзвуковым скоростям:
сечение ядра увеличивается по течению. Давление внешней среды „проникает” через дозвуковую часть пристеночного слоя внутрь выходного участка, и давление на стенке оказывается более низким, чем давление на осп.
Следует подчеркнуть, что перестройка течения на выходном участке трубы сопровождается резким изменением профиля скорости в пристеночном слое.
в зависимости
от М по данным МО ЦКТИ и МЭИ. Зависимость С от Re
— ?
На рис. 5-10 нанесены значения С =4-
|
0 | |||||||||||
| - | О < | 1пыть | /МЭИ | ||||||||
| - |
* Опыты МО цкт III. | ||||||||||
0,7
0,9
КО
Рис. 5-10. Зависимость коэффициента сопротивления от числа М при дозвуковых скоростях по данным МО ЦКТИ и МЭИ.
при больших дозвуковых скоростях согласно опытным данным сохраняется практически такой же, как и для несжимаемой жидкости. Следовательно, отношение С, взятое при одинаковых значениях Re, отражает влияние только числа М.
График на рис. 5-10 показывает, что при М<< 0,70-й),75 коэффициент сопротивления не зависит от М и весьма близок к С . Для этой области расчет С может производиться по любой эмпирической формуле [например, (5-26)] или по кривым ВТИ*.
В диапазоне чисел М = 0н-0,8 и Re — 3-103 -г- 3-105 удовлетворительно совпадает с опытом формула, полученная в МЭИ:
C=0,0334Re7°'2, (5-27)
* В последнем случае необходимо убедиться в том, что для шероховатых труб влияние сжимаемости на S при М < 0,7 ч- 0,8 будет также невелико. Это предположение нуждается в опытной проверке.
где Re =Re;t — число Re, отнесенное к длине трубы.
/,г ко 0,8 0,6 о,ь Q2
оА
о,з
0,8
0,8
При М > 0,7 н- 0,75 коэффициент сопротивления трубы уменьшается с ростом М; особенно интенсивное снижение С наблюдается при скоростях М > 0,85.
Напомним, что изменение давления на элементарном участке трубы dx выражается известной гидравлической формулой:
dp = ^F-^-dx.
Разность сил давления, действующих на выделенный элемент жидкости, при равномерном движении в трубе равна силе трения на стенке трубы, т. е.
71D2 , J-.J 71D2 r PC2 ,
— dp = *0TiDdx = -j- С dx.
Отсюда можно получить формулу, связывающую напряжение трения на стенке и С:
В соответствии с формулой (5-28) результаты изложенного выше опытного исследования можно выразить так: влияние сжимаемости, заметно проявляющееся при ЛГ>0,75, приводит к некоторому уменьшению силы трения, отнесенной к кинетической энергии потока в данном сечении.
Физически этот результат объясняется тем, что с ростом числа М увеличиваются градиенты давления в трубе (рис. 5-8). Возрастание градиентов давления в конфузорном течении вызывает деформацию профиля скорости у стенки; наполнение профиля скорости увеличивается. Кроме того, пристеночный слой при этом утоняется.
Околозвуковой поток особенно чувствителен к изменению сечения, что видно из уравнения (5-8). Поэтому на концевом участке трубы, где М. 0,9, наблюдаются весьма большие отрицательные градиенты давления и соответственно резкое снижение С.
Резкое уменьшение ? при М > 0,9 связано также с тем, что область скоростей М = 0,9-^1,0 расположена вблизи концевого участка трубы, где пристеночный слой нарушается. При расчете по формуле (5-28) значительная деформация профиля скоростей на выходном участке трубы не Гучитывается.
Оценивая влияние сжимаемости на коэффициент сопротивления трубы при сверхзвуковых скоростях, необходимо различать три основных режима течения в трубе. Первый режим отвечает бесскачковому движению потока, скорости которого в каждом сечении трубы сверхзвуковые. Как уже было показано, такой режим возможен, если длина цилиндрической трубы меньше предельного значения ('/ -< '/макс). Если же в трубе имеется соответствующий источник возмущения, ТО при Х<СХчакс сверхзвуковой поток может быть насыщен скачками уплотнения. Возмущение потока в трубе может быть вызвано угловым поворотом стенки, который образуется в сечении стыка сопла Лаваля с трубой. В простейшем случае расширяющаяся часть сопла выполняется конической с различными углами раствора. Чем больше угол раствора сопла, тем больше угол отклонения потока при входе в трубу и тем интенсивнее скачок, образующийся в точке поворота стенки. Такие режимы течения с коническими скачками, когда поток вплоть до выходного сечения остается сверхзвуковым, составляют вторую группу режимов. Наконец, если Х>ХМакс>Т0 внутри трубы возникает сложная система скачков, за которой поток будет дозвуковым; это — третья группа режимов течения. Распределение параметров течения по длине трубы в тех указанных случаях оказывается существенно различным.
Для третьей группы режимов, когда в результате скачков поток становится дозвуковым, характер распределения давления по данным Неймана и Лустверка показан на рис. 5-11 (для Х1 = 2,2). По мере повышения давления в выходном сечении трубы система скачков перемещается к соплу. Интенсивность скачков при этом повышается. Отметим, что протяженность системы скачков оказывается значительной. За системой скачков поток дозвуковой, и давление вдоль трубы падает.
В соответствии с различным характером распределения давлений по цилиндрической трубе при сверхзвуковых скоростях будут различными и коэффициенты сопротивления. При равномерном сверхзвуковом потоке в трубе (без скачков) коэффициент сопротивления имеет наименьшее значение.
На рис. 5-12 нанесены значения коэффициента сопротивления в зависимости от М по данным МО ЦКТИ для интервала чисел М = 0-г-1,65. Здесь воспроизведены опытные точки С для дозвуковых скоростей, частично представленные на рис. 5-8, и добавлены результаты более поздних исследований для М. > 1. Характерным для области небольших сверхзвуковых скоростей следует считать заметное возрастание здесь коэффициент сопротивления меняется от 0,007 до 0,018.
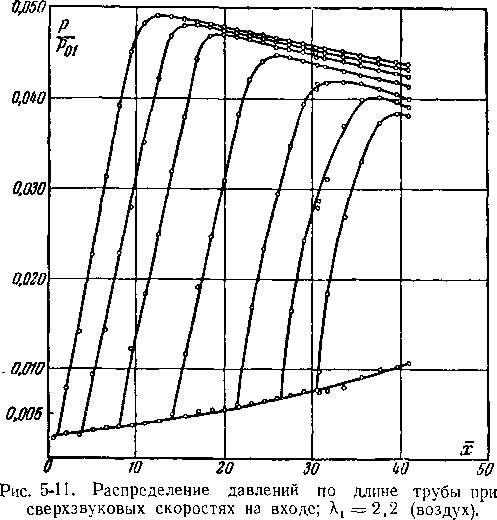
Можно предположить, что на этом участке происходит турбулизация пристеночного слоя в трубе, т. е. переход его из ламинарного режима в турбулентный70. В предыдущей области М = 0,95-г-1,03, где градиенты давления достигают максимальных значений, по-видимому, происходит ламинаризация пристеночного слоя, так как при больших отрицательных градиентах давления интенсивность турбулентных пульсаций снижается.
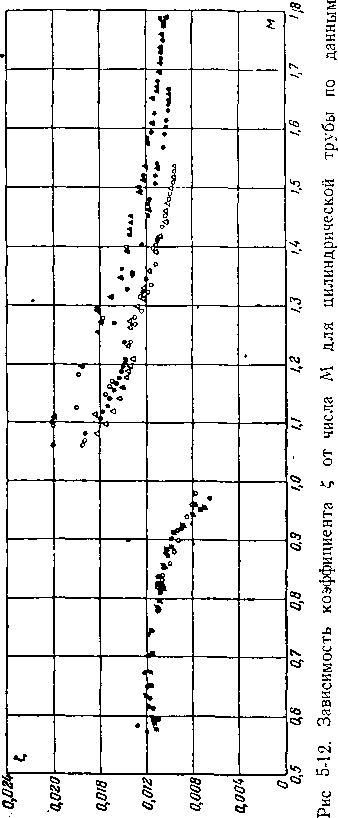
МО ЦКТИ.
На участке М = 1,25 -г- 1,6 С снижается и при М = 1,65 достигает минимального значения С ~ 0,01. Это снижение объясняется наполнением профиля скорости в области сверхзвукового течения с отрицательными градиентами давления.
При М>1,3 влияние числа Рейнольдса на С невелико.
5-6. ПОГРАНИЧНЫЙ СЛОЙ. ОСНОВНЫЕ ПОНЯТИЯ И УРАВНЕНИЯ1
Современные представления о механизме сопротивления тел, обтекаемых потоком газа, и методы расчета сопротивления основываются на теории пограничного слоя2.
Как показывает опыт, при больших числах Re влияние вязкости сосредоточивается в области потока, непосредственно прилегающей к поверхности тела. Эта область имеет малую по сравнению с длиной протяженность в направлении нормали к поверхности тела и называется пограничным слоем. Вне пограничного слоя поток имеет пренебрежимо малую завихренность и на этом основании рассматривается как потенциальный. В пограничном слое скорости меняются от нуля на поверхности тела до скорости потенциального потока на внешней границе. Так как толщина слоя невелика, то градиенты скоростей в этой области достигают больших значений и, следовательно, поток здесь обладает большой завихренностью.
Характер распределения скоростей в пограничном слое на плоской стенке показан на рис. 5-13. Непосредственно на стенке жидкость „прилипает“ к поверхности (Я5 = 0). В тонком пограничном слое с удалением от поверхности тела скорости меняются весьма интенсивно и на небольшом расстоянии от поверхности достигают скорости внешнего потока.
Сопротивление обтекаемых тел существенно зависит от режима течения в пограничном слое. Движение жидкости в пограничном слое может быть ламинарным или турбулентным.
Законы изменения скорости по нормали к поверхности для ламинарного и турбулентного режимов должны быть различными.
Так как скорости в пограничном слое меняются от нуля на стенке, то естественно предположить, что некоторый участок пограничного слоя, прилегающий к стенке, всегда находится в ламинарном режиме. Это предположение подтверждается распределением скоростей у стенки в пограничном слое.
Рассмотрим более подробно условия образования пограничного слоя на поверхности крылового профиля (рис. 5-13).
В направлении потока вдоль поверхности толщина пограничного слоя 8 увеличивается. Заметим, что понятия внешней границы и толщины пограничного слоя не являются определенными, так как изменение продольных скоростей при переходе из пограничного слоя во внешний поток происходит плавно. Приближенно внешняя граница слоя определяется в тех точках, где продольная скорость отличается от скорости внешнего потока на малую величину порядка 1°/0.
Внешняя граница пограничного слоя не совпадает с линией тока, так как частицы внешнего потока непрерывно проникают в пограничный слой (рис. 5-13).
Передний участок слоя, расположенный вблизи носика профиля, обычно является ламинарным. На небольшом расстоянии от носика (сечение II на рис. 5-13,а и б) обнаруживается ламинарный профиль скоростей. В некотором сечении III начинается переход ламинарного упорядоченного движения в турбулентное, которое носит пульсационный характер.
В переходной зоне течение в пограничном слое смешанное: значительная часть слоя, ближайшего к поверхности, находится в ламинарном режиме.
За переходной областью развивается устойчивый турбулентный слой. Здесь область ламинарного подслоя настолько мала, что экспериментально ее трудно обнаружить. Как видно из рис. 5-13,6, турбулентный слой имеет более полный профиль скоростей.
Схема образования пограничного слоя на рис. 5-13 изображена не в одинаковом масштабе по осям л: и у. Толщина слоя 8 весьма невелика по сравнению с размерами тела и составляет сотые ц тысячные доли хорды профиля.
Расчет ламинарного пограничного слоя основывается на дифференциальных уравнениях энергии (5-3) и движения вязкой жидкости (5-4). Используя отмеченные выше физические особенности движения в слое, уравнение (5-4) можно существенно упростить.
С этой целью перейдем в уравнениях (5-4) к безразмерным величинам. Для простоты рассмотрим установившееся движение несжимаемой жидкости. В качестве мае-
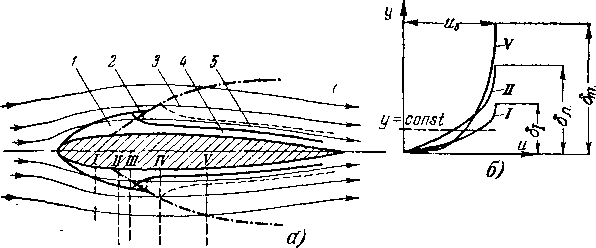
Рис. 5-13. Схема образования пограничного слоя на поверхности крылового профиля, в—изменение толщины и структуры слоя вдоль поверхности: 1—ламинарный участок слоя; 2—переходная область; «? — турбулентный участок слоя; 4—ламинарный подслой; 5 —переходный слой; б —распределение скоростей в различных
сечениях слоя.
штабов продольных скоростей и координат выберем некоторую характерную скорость и0 и характерный линейный размер L0. Масштабы поперечных скоростей и координат обозначим соответственно у0 и 8. Обозначим масштабы для давлениями плотности р0 и р0. Тогда после преобразований, аналогичных преобразованиям § 5-2, получим следующую систему уравнений:
ди | ?°и° ди__р0р др, у д2и , vZ,0 д2и.
U 5и0V ду рм2 йхТ 10к0 дх2'82и0 ду2 ’
дл: 8и0 ду
Масштабы величин, входящих в систему уравнений (5-29), можно выбрать на основании следующих соображений. Если масштабы и0 и L0 выражают характерную скорость и линейный размер обтекаемого тела, то величины v0, 8, p0 и p0 пока остались неопределенными. Пользуясь этим произволом, уравнения (5-29) нетрудно привести к каноническому виду.
Действительно, полагая /V=PMo , Ро— 1 полуЧИм р-^°= 1, а
Р“о
поперечные масштабы у0 и 8 выберем таким образом, чтобы коэффициенты и были постоянными и не зависели от числа Re.
Положим
Lv
-•=1 и
1.
Принципиально эти комплексы можно приравнять любой постоянной, но в данном случае выражения для поперечных масштабов получаются наиболее простыми.
Решая написанную систему относительно »0 и 8 для масштабов поперечных скоростей нелинейных размеров, получаем следующие значения
(5-30)
V Re
При этом уравнения (5-29) примут вид:
ди
' дх
ди др .
ду cto^Re дх
1 д2и г д2и
_1_
Re
' da , dv \ др |
+
(5-31)
du.dv дх ' ду
1 d2v Re2 дх2
0.
ду2'
1 d2v. Re ду2'
Если допустить, что неизвестные величины и, v, р и их производные с увеличением числа Рейнольдса стремятся к определенным пределам в фиксированных точках, то при больших Re в уравнениях (5-31) можно отбросить все чле-
1 1
ны, имеющие множители ^ и , как малые величины по сравнению с другими членами.
rf результате перехода вновь к размерным величинам получим дифференциальные уравнения ламинарного пограничного слоя в форме Л. Прандтля:
du I ida 1 др , д2и.
U г--f“ V -д— — г--j— V -г 2 >
дх 1 ду р дх 1 ду2
![]()
ди I ди
дх'ду
(5-32)
Система (5-32) должча быть решена при следующих граничных условиях:
у = 0; ц = 0; у = 0;
у оо; и—* и (х).
Последнее условие означает, что скорость в пограничном слое переходит асимптотически к скорости внешнего потока. В действительности этот переход, как уже отмечалось, происходит при значении у, соизмеримом с поперечным масштабом 8.
Полученное условие означает, что распреде
ление давлений на внешней границе слоя и на поверхности обтекаемого тела совпадает. Отсюда следует, что во всех точках поперечного сечения слоя давления одинаковы, т. е. давление внешнего потока передается через пограничный слой к поверхности тела без изменения.
Условие ~ = 0 позволило объяснить весьма важное дУ
явление отрыва пограничного слоя. Рассмотрим обтекание некоторой криволинейной поверхности АВ (рис. 5-14), предполагая, что давление внешнего потока вдоль этой поверхности вначале уменьшается, достигает минимального значения в точке М и затем увеличивается. Участок внешнего потока, в котором градиенты давления отрицательны
(^<0\ называется конфузорным участком. Область течения за точкой Af, характеризуемая положительными градиентами давления , называют диф-
![]()
фузорным участком. На конфузорном участке внешний поток ускоряется, а на диффузорном — тормозится.
Учитывая, что в пограничном слое |^ = 0, заключаем, что
совершенно аналогичное распределение давлений имеет место и вдоль поверхности АВ на любом расстоянии у<СР в пограничном слое.
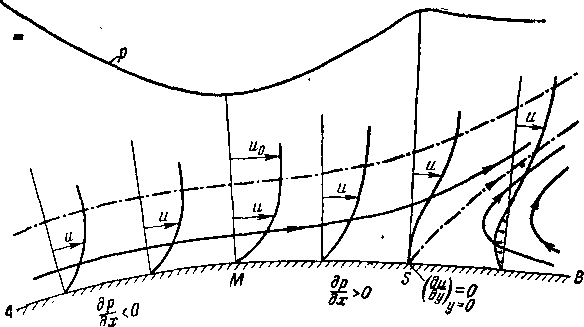
Рис 5-14. Схема образования отрыва пограничного слоя.
В пределах пограничного слоя скорости перед точкой М увеличиваются, а за нею — уменьшаются (см. эпюры скоростей на рис. 5-14). Частицы жидкости вблизи стенки обладают малой кинетической энергией, причем в диффу-зорной области вдоль поверхности АВ запас кинетической энергии частиц уменьшается. В результате в некотором сечении S частицы у стенки не могут преодолеть тормозящего влияния внешнего потока и останавливаются. Эпюра скоростей принимает характерную остроконечную форму. На стенке кривая скоростей удовлетворает условию
![]()
' (5-32а)
Дальше за точкой S под воздействием перепада давлений, направленного против течения, начинается возвратное движение частиц у стенки. Встречаясь с основным потоком, возвратно движущиеся частицы оттесняются от стенки, что и приводит к отрыву пограничного слоя и к резкому увеличению его толщины. За точкой отрыва S эпюра скоростей имеет также весьма характерную петлеобразную форму, причем непосредственно у стенки
![]()
Изложенное показывает, что отрыв пограничного слоя при обтекании плавйой стенки может происходить только в диффузорной области.
Используя уравнения (5-32), легко показать, что положение точки отрыва ламинарного пограничного слоя не зависит от числа Re. Действительно, решение системы (5-32), дает:
u = f(x,y), (5-326)
где х и у — безразмерные координаты.
Тогда, продифференцировав по у и используя в точке отрыва условие (5-32а), получим;
f'(xs, 0) = 0.
Поскольку масштаб по оси х от числа Re не зависит, приходим к выводу, что координата точки отрыва ламинарного слоя также не зависит от числа Рейнольдса.
5-7. УСЛОВНЫЕ ТОЛЩИНЫ И ИНТЕГРАЛЬНОЕ СООТНОШЕНИЕ ДЛЯ ПОГРАНИЧНОГО СЛОЯ
Выше указывалось, что понятие толщины пограничного слоя не имеет точного количественного смысла. Действительно, скорость в пограничном слое и с ростом у асимптотически приближается к значению скорости внешнего потока и0. Величина 8 зависит от того, где выбрана точка, условно показывающая границу слоя.
Поэтому в расчетах пограничного слоя вводятся другие интегральные толщины, зависящие от S: толщина вытеснения 8*, толщина потери импульса 8’* и толщина потери энергии 8*".
Для выяснения физического смысла указанных толщин сравним течение идеальной и вязкой жидкостей около твердой стенки (рис. 5-15).
При отсутствии трения за единицу времени через поперечное сечение потока высотой dy и шириной, равной единице, протечет масса раийёу. В пограничном слое за то же время через сечение dy протечет масса рudy.
Разность^этих количеств составит:
ОО
о
О 5
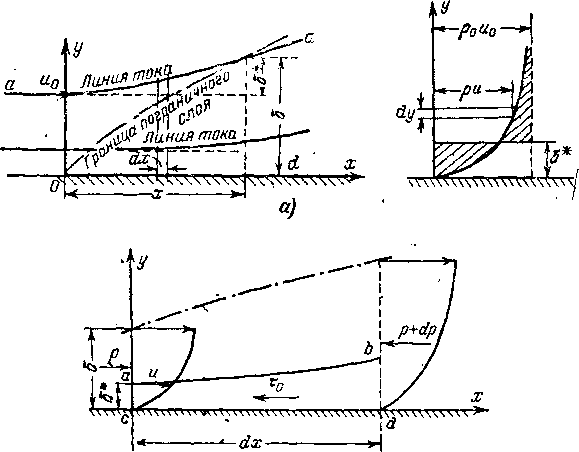
Рис. 5-15. К определению условных толщин пограничного слоя (а). К выводу уравнения импульсов для пограничного слоя (б).
е)
Второй интеграл правой части мал по сравнению с первым. Поэтому интегрирование достаточно проводить только в пределах физической толщины слоя 8.
Разделив найденный излишек массы на р0и0, получим:
Величина 8* показывает смещение линии тока в направлении внешней нормали к контуру обтекаемого тела.
Вместе с тем 6* характеризует уменьшение расхода жидкости через сечение слоя, „нормальное* к стенке, обусловленное „вытеснением” жидкости пограничным слоем, и поэтому носит название толщины вытеснения.
Толщина потери импульса 6** равна такой толщине слоя жидкости, движущейся со скоростью и0 вне пограничного слоя, количество движения которой равно импульсу сил трения в пограничном слое. Это количество движения, „потерянное" в пограничном слое, будет равно:
ь г
ри (й0 — и) dy = Г рии0 ГI — ~ j dy.
о
о
Разделим полученное выражение на раий . Тогда полу
чим:
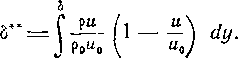
О
Масса жидкости рudy теряет в пограничном слое кине-
тическую энергию, равную ?и. (и0 — и?) dy. Для всего слоя эта потеря составит:
5
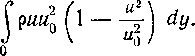
Тогда толщина потери энергии
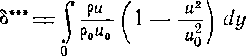
представляет собой толщину движущейся вне слоя жидкости, обладающей кинетической энергией, потерянной в пограничном слое.
Для решения задач о течении сжимаемой жидкости в ряде случаев целесообразно иметь одинаковую структуру формул, определяющих интегральные толщины. Поэтому наряду с формулой (5-33) толщину вытеснения §71 часто подсчитывают по формуле
(5-36)
S
![]()
о
При этом, естественно, нарушается приведенный ранее физический смысл толщины вытеснения. Для несжимаемой жидкости уравнения (5-33) и (5-36) оказываются тождественными.
Решение задачи о сопротивлении тела в потоке вязкой жидкости при безотрывном обтекании сводится к установлению распределения сил трения вдоль обтекаемых поверхностей тела, а следовательно, к расчету пограничного слоя.
Широко распространенный приближенный метод расчета основывается на оценке изменения количества движения в пограничном слое. Произведем такую оценку.
Из определения толщины вытесненйя следует, что всю массу жидкости, протекающей в пограничном слое, можно условно заменить массой, расположенной между линией ab и стенкой ей (рис. 5-15), скорость которой равна нулю („вытесняемая" масса), и массой, протекающей выше ab
со скоростью и .
о
Со стороны стенки на вытесняемую массу действуют силы трения, а в направлении течения будут приложены силы давления. Скорости выше линии вытеснения ab равны и0 — иа(х) и в пределах рассматриваемого объема на основании дифференциальных уравнений пограничного слоя
(5-32) ~ = 0. Применяя уравнение импульсов, можно найти
величину потери количества движения на участке dx:
(5-37)
dl = x0dx~\- dpb*,
где tadx и dpb* — секундные импульсы сил трения и сил давления, действующих на „вытесняемую" массу жидкости.
Количество движения I на основании уравнения (5-34) можно выразить через толщину потери импульса:
/= Ро«о8**-
Поскольку на внешней границе пограничного слоя течение считается потенциальным, продольный градиент давления ^ легко выражается на основании уравнения Бернулли через скорости и0 и плотность р0:
dp du„ ’
dx ~~ ~ Р°йо 5F ~ РоМо«0-
Подставляя эту величину в (5-37), находим:
р(5-37а)
Заменим далее
_ ^Ро
dx~dp'dx~ a\ Po 0 »
и разделим (5-37a) на р0и*. В результате получим для сжимаемой жидкости следующее уравнение:
ij+if-(2 + tf-M0) = -^V. (5-38)
“0 Ро"о
Здесь
Уравнение (5-38) носит название интегрального соотношения, так как величины 8** и 5* выражаются интегралами (5-33) и (5-34).
Интегральное соотношение (5-38) для пограничного слоя можно получить, не прибегая к понятию толщины вытеснения. С этой целью уравнение импульсов применяется к объему жидкости, заключенному между двумя бесконечно близкими поперечными сечениями пограничного слоя
(рис. 5-15,6). Подставляя в (5-38) выражения для условных толщин 8*, 5** и заменяя и^ через ^, после преобразований находим:
щйу = — т0— 8^-. (5-39)
JL
dx
j рu2dy
![]()
о
о
Для несжимаемой жидкости получим:
г
г
![]()
о
о
Интегральное соотношение для пограничного слоя пригодно для расчета как ламинарного, так и турбулентного пограничных слоев, так как при его выводе не делалось никаких предположений относительно касательного напряжения х0. Эта величина определяется' различно в зависимости от режима течения жидкости в пограничном слое, что и является отражением различной природы трения при ламинарном и турбулентном движениях.
| При возникновении отрыва уравнение импульсов может служить для определения положения точки отрыва, в кото-
![]()
5-8. ОБЩЕЕ ВЫРАЖЕНИЕ ДЛЯ КОЭФФИЦИЕНТА СОПРОТИВЛЕНИЯ ТРЬНИЯ В ПОГРАНИЧНОМ СЛОЕ ПРИ НАЛИЧИИ ГРАДИЕНТА ДАВЛЕНИЯ
В уравнении импульсов содержатся две искомые переменные величины: толщина слоя 8 (или взаимосвязанные условные толщины 8* и 8**) и напряжение трения на стенке т0.
В общем случае т0 определяется скоростью на внешней
fff
U
границе пограничного слоя, ее производными , и0 и
т. д., характерным размером, например толщиной потери импульса 8**, плотностью р, температурой Т и коэффициентом кинематической вязкости v.
Используя основные положения теории размерности, из функциональной зависимости (5-40) нетрудно получить структурную формулу для коэффициента сопротивления.
Примем в качестве основных размерности скорости й0, плотности р, длины §** и температуры Т. Простой проверкой легко убедиться, что, комбинируя указанные величины, можно получить размерности всех остальных параметров. Действительно, т0 имеет размерность л:г/ж2. Ту же размерность будет иметь и комплекс рм0: [кг-сек2/м*-м2/сек2]. Следовательно, отношение ^0/р0Мд, представляющее собой местный коэффициент трения cfi окажется безразмерным. Переходя в выражении (5-40) от размерных величин к безразмерным, получим
¦с. ( и'пд** и’’ 8**2 \
и §**
Здесь Re**== --число Рейнольдса, подсчитанное
по толщине потери импульса.
Число безразмерных параметров в выражении (5-41) можно сократить, если принять, что напряжение трения определяется так же, как и в случае ламинарного течения только первой производной скорости мо-
Это предположение подтверждается для конфузорных течений и течений при небольших положительных градиентах давления. Вблизи точки отрыва роль старших производных возрастает, и здесь сохранение только первой производной уже недостаточно.
Далее, можно показать, что при отнесении физических постоянных v и р к температурным условиям на стенке число М исключается из зависимости (5-41). Таким образом, с учетом принятых допущений
(М2)
? ? tf ф ¦ #
Где Re^ = ——, чт— кинематическая вязкость, подсчитан-
ная по температуре стенки.
О
* * \
+
Р®“о
^(RO + 'MRC)
Здесь cf—местный коэффициент трения, подсчитанный по плотности у стенки рда.
Выражение (5-43) является общим как для ламинарного, так и для турбулентного режимов течения в пограничном слое. В зависимости от режима течения коэффициенты <|>0, 4*!, ф2 и т. д. будут принимать различные значения.
Найдем конкретный вид выражения (5-43) для ламинарного течения. С этой целью запишем (5-43) в таком виде:
h.
Фо
(5-44)
1 +
+•
'f
—V = lh
При «о = 0 формула (5-44) должна совпадать с соответствующей формулой для коэффициента сопротивления плоской пластинки при безградиентном ее обтекании.
В этом случае задача решается достаточно точно путем численного интегрирования системы (5-32) и независимо от метода решения для безградиентного течения коэффициент сопротивления cf0 выражается формулой
До
^0 = Ф»:
Re*
где а0 — постоянная величина. Следовательно,
Re*
В точке отрыва t0 = 0; в этом случае выражение в квадратных скобках должно обращаться в нуль. Учитывая, что положение точки отрыва не зависит от числа Re**, получим: Ф1= const; фв = const; ф3 = const и т. д. Отсюда
и08**г
Коэффициенты а0, at, а2 и т. д. в общем случае определяются экспериментально. Однако для ламинарного пограничного слоя их можно определить и теоретически. Так, например, А. М. Басин получил а0 = 0,22; а1=1,85; а2 = — 7,35.
Обозначим
![]()
(5-46)
и
(5-47)
тогда
![]()
(5-48)
Параметр f часто называют формпараметром; как будет показано ниже, он определяет форму профиля скорости в ламинарном пограничном слое. Следует отметить, что структура формпараметра, содержащего производную
du„
, отражает влияние продольного градиента давления
внешнего потока.
Для турбулентного слоя многочисленные эксперимен-
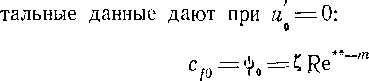
(5-49)
и для коэффициента сопротивления получается из (5-44) следующая формула:
(5-50)
Здесь
![]()
(5-51)
Параметр Г (параметр Бури), так же как и формпара-метр f, отражает влияние продольного градиента давления и числа Рейнольдса на профиль скоростей в турбулентном слое.
Зная зависимость для cf и закон изменения величины
# = ~ в зависимости от продольного градиента давле-
ния, нетрудно получить из интегрального соотношения (5-38) дифференциальное уравнение для определения толщин пограничного слоя.
Рассмотрим отдельно решение уравнения (5-38) для ламинарного и турбулентного слоев.
5-9. РАСЧЕТ ЛАМИНАРНОГО ПОГРАНИЧНОГО СЛОЯ ПРИ НАЛИЧИИ ГРАДИЕНТА ДАВЛЕНИЯ
Расчет пограничного слоя сводится к решению интегрального соотношения (5-38) [или (5-39)], которое содержит три неизвестные величины: толщину потери импульса 8**, коэффициент сопротивления с, = -~ и вели-
{ Р«5
Следовательно, для решения задачи необходимо иметь еще два дополнительных соотношения, связывающих указанные величины. Используя общее выражение (5-48) для коэффициента сопротивления и рассматривая для простоты случаи несжимаемой жидкости, получим уравнение с двумя неизвестными: 8** и Н, связь между которыми нетрудно получить, если известен профиль скорости в пограничном слое.
В общем случае скорость в поперечном сечении слоя зависит от местного градиента давления и расстояния от стенки у. Влияние градиента давления учитывается форм-параметром f. Следовательно, относительную скорость в точке слоя можно представить в таком виде:
Тогда
00
••“JO-
о
оо
О
оо
о
Проинтегрировав полученное выражение в указанных пределах, найдем:
Далее, подставив в уравнение (5-38) зависимости (5-48) и (5-52), получим после несложных преобразований дифференциальное уравнение первого порядка относительно форм-параметра /:
ал Uq и0
Здесь
F=2{Z(f)-2f[2 + If(f)1}.
Конкретный вид функции F (f) зависит от формы профиля скорости в пограничном слое. Вычисления показывают, что F (f) очень мало отличается от линейной функции, т. е.
F(f) = a~bf.
При этом уравнение (5-53) переходит в линейное относительно параметра / уравнение
df
-т~ — а dx
интеграл которого имеет вид:
г X ,
'“о (* ь—1 , | иа
* dx + c .
Если при л: = 0 и0 = 0, то из условия конечности f следует положить постоянную интегрирования с = 0.
В практике удобнее вести расчеты, пользуясь безразмерными величинами.
Положив и0'=~ и х=-^-, где — скорость набегающего потока, a L — длина обтекаемой поверхности, получим:
Постоянные а и b могут быть приняты соответственно равными 0,45 и 5,35. *
Для толщины потери импульса получим:
Далее, по формуле (5-48) нетрудно определить местный коэффициент сопротивления cf и по выражению 8* =
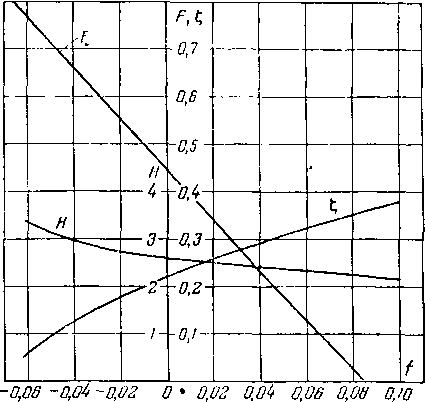
Рис 5-16 Зависимость величин $, F и Н от параметра f.
= Н (f) S** — толщину вытеснения. Значения функций С (/) и Н (/) приведены на рис. 5-16.
Рассмотренный метод расчета может быть распространен и на случай течения сжимаемой жидкости, если перейти к новым переменным, предложенным А. А. Дородницыным
о о
(5-56)
k + 1 0) о
Расчет по формулам (5-48), (5-54), (5-55) и (5-56) оказывается относительно простым и обеспечивает вполне удовлетворительную точность.
Для примера рассчитаем ламинарный пограничный слой на плоской пластинке. Здесь и0 = const; и0 = 0; f = 0 и т=\.
Тогда из (5-55), (5-47) и (5-48) получим:
I f 0,45ч
= S**L=L у -^j-; С (/) = 0,22;
с. = 0,22 —rjnr =-7=5= = 0,332 У —j >
f ’ иа8** Г 0,45м! У u0L
/0,45м 3,332 |/^ •
2 _ п ччо 1 / -'^1. (5-57)
"'о = с/Р“о = 0
5-10. ПЕРЕХОД ЛАМИНАРНОГО ПОГРАНИЧНОГО СЛОЯ В ТУРБУЛЕНТНЫЙ
При определенных условиях ламинарный пограничный слой теряет устойчивость и переходит в турбулентный. Ориентировочно границу потери устойчивости ламинарного течения можно установить по критическому числу Рейнольдса ReKp. Пользуясь аналогией между явлениями перехода ламинарного режима в турбулентный в цилиндрической трубе и в пограничном слое, можно, как это уже указывалось, ввести характерные для слоя числа Рейнольдса, отнесенные к толщинам72 8, 8* и 8**:
Re.= -^; Re* = -^; Re** = ^ .
v 5 V ’ V V
Опытные данные показывают, что критические значения числа Re5 пограничного слоя имеют тот же порядок, что
и для труб, но могут колебаться в более широких пределах (Re8 — 2 ООО 5 ООО). Согласно многочисленным
исследованиям критическое число ReKp зависит в основном от состояния поверхности обтекаемого тела, степени турбулентности (возмущенности) внешнего потока и градиента скорости, т. е. параметра f.
Теоретические и экспериментальные исследования устойчивости ламинарного пограничного слоя показали, что „потеря устойчивости” происходит либо в результате наложения возмущений, вызванных срывом с бугорков шероховатости на поверхности обтекаемого тела, либо вследствие конечных возмущений, вносимых в пограничный слой внешним потоком. Первая причина оказывается существенной только при малой турбулентности набегающего потока (порядка 0,1°/0) и большой шероховатости.
Используя общие положения теории размерности и опытные данные, нетрудно получить соответствующую зависимость в явном виде. Опуская вырод, запишем формулу для определения Re**, полученную А. П. Мельниковым:
![]()
(5-58)
где Е0 — начальная степень турбулентности; f — формпараметр;
fs — значение формпараметра в точке отрыва; для ламинарного слоя можно принять /а = — 0,085.
Таким образом, для определения точки потери устойчивости ламинарного пограничного слоя нужно найти по уравнению (5-55) изменение толщины потери импульса вдоль поверхности рассматриваемого тела и построить кривые Re”=cp(x) [уравнение (5-58)] и Re** = (х) =
Точка пересечения указанных кривых будет- представлять собой искомую координату хкр.
Результаты экспериментального исследования показывают, что переход ламинарного пограничного слоя в турбулентный происходит в некоторой области, размеры которой зависят от местного градиента давления, чисел М и
Re, степени турбулентности и некоторых других факторов.
Определение положения и протяженности переходной зоны, а также характера изменения о в этой зоне составляет важную часть задачи по расчету смешанного слоя и, в частности, последующего турбулентного участка73.
Переходная область может быть определена экспериментально путем измерения профилей скорости в различных сечениях по длине поверхности. Характер изменения профиля скорости в переходной области можно проследить на рис. 5-17, а. На расстоянии х = 35 мм от передней кромки пластины слой — ламинарный; все точки образуют
кривую, соответствующую уравнению ^=2 у — 2^|-j-{-
-j-^У . При переходе в сечение х ^ 50 мм профили
скорости резко деформируются и приобретают форму, типичную для турбулентного пограничного слоя.
Профили скорости в пограничном слое позволяют вычислить толщину потери импульса 6 (х) и по характеру изменения этой величины установить протяженность переходной зоны (рис. 5-17,6).
Длину переходной области s принято определять в долях общей длины обтекаемой поверхности.
Изменения 8 *в этой области характеризуются величиной
** »** т-ч
где ReK, 5к — число Re и толщина потери импульса в **
** ТЛ ***
конце и ReH= —число Re и он в начале переход-
ной области. При безградиентном течении величина г =
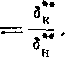
В общем случае г** зависит от профиля скорости в начале переходной зоны, чисел Re и М, степени турбу-
**
лентности. С увеличением чисел Re и М величина г несколько возрастает (рис. 5-18). По опытам МЭИ измене-
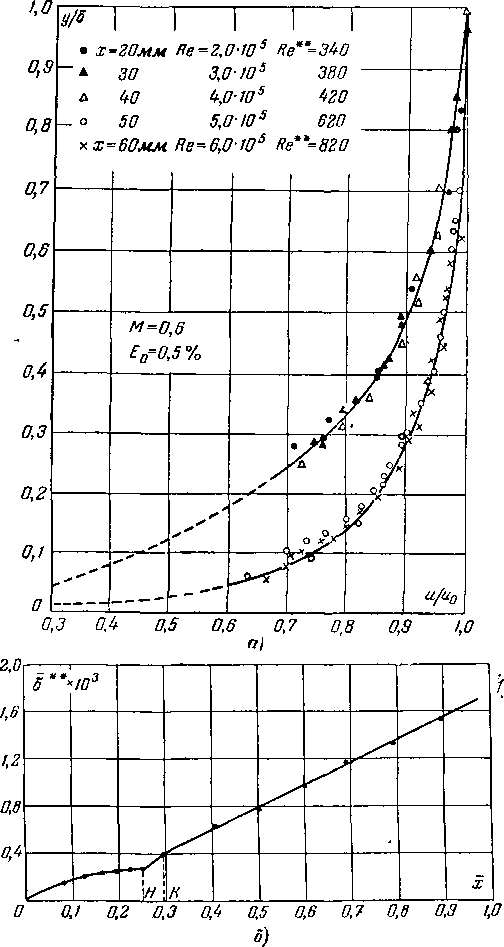
Рис. 5-17.
а_изменение профиля скорости в пограничном слое вдоль плоской стенки; б —¦•
изменение толщины потери импульса вдоль плоской стеики.
ние Е„ в пределах 0,5—1,5°/0 не приводит к заметным изменениям величины г**. Дальнейшее увеличение Е0 вызывает
резкое уменьшение г .
Для характеристики влияния профиля скорости на рис. 5-19 показан график (/<,), где /0—формпараметр
в начале переходной зоны. Как следует из кривой, с ростом формпараметра г" возрастает. Аналогично в зависимости от формпараметра /0 изменяется и протяженность переходной зоны s (рис. 5-19). Такое поведение кривых г* = <Pj (f0) и s = <р2 (/„) можно объяснить следую-
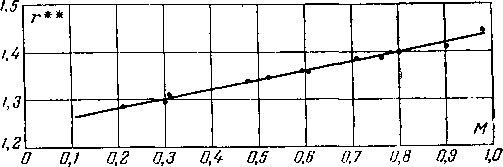
Рис 5 18 Зависимость величины г" от числа М.
щим образом. В переходной зоне вследствие поперечного перемещения частиц толщина пограничного слоя 8 увеличивается, а профиль скорости становится более полным. Если в результате роста толщины 8 происходит увеличение 8", то увеличение полноты профиля скорости вызывает падение интегральной толщины 8 *. В конфузорной области основное значение имеет возрастание толщины пограничного слоя 8, ибо здесь профиль скорости достаточно полный и в результате перехода его полнота изменяется незначительно74. Наоборот, в диффузорной области в результате перехода ламинарного течения в турбулентное происходит значительная деформация профиля скорости, причем эта деформация оказывается тем большей, чем больше положительный градиент давления в месте, где происходит переход.
При некотором значении параметра f в диффузорной области оба фактора, влияющие на величину 8'*, взаимно
**
компенсируются и величина г оказывается равной 1. Протяженность переходной зоны при этом также оказывается незначительной. По опытам МЭИ г* = 1 при / =—0,06-=-
— 0,07.
Если же по какой-либо причине переход начнется при — 0,07, то, по-видимому, процесс турбулизации слоя и перестройка профиля скорости будут происходить против течения, пока профиль ламинарного слоя не окажется достаточно устойчивым.
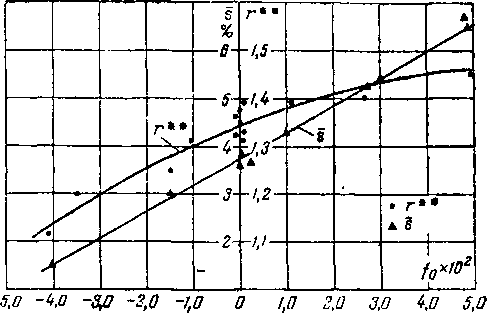
Рис 5-19 Зависимость вел гаин г** и 5 от формпараметра
Отсюда, между прочим, следует, что отрыв пограничного слоя может произойти только в области либо ламинарного, либо турбулентного движения, так как переход ламинарного слоя в турбулентный в диффузорной области происходит при значении параметра /, меньшем, чем его значение в точке отрыва.
На основании обработки опытных данных для расчета переходной области получены следующие эмпирические формулы:
5^^)°''5(3,7 + 5,5Шо: (5-59)
0 12f;r
г -(7-Ь100/о) 2 +0,12М. (5-60)
«-V --**
Зная величины s и г , легко наити координаты сече-ния, от которого следует вести расчет турбулентного слоя, и значение в нем толщины потери импульса.
5-11. РАСЧЕТ ТУРБУЛЕНТНОГО ПОГРАНИЧНОГО СЛОЯ
Расчет турбулентного пограничного слоя строится на экспериментальных данных, позволяющих приближенно выразить напряжение трения в слое.
Во многих случаях удобно пользоваться приближенным степенным законом распределения скоростей в слое, выражаемым формулой
![]()
(5-61)
Формула (5-61) построена на основании сравнения профилей скорости в турбулентном слое и в цилиндрической трубе. Как было показано, профиль скоростей в трубе меняется при изменении числа Re (рис. 5-6). Следовательно, показатель п в формуле (5-61) является функцией числа Рейнольдса. Так, по опытам Н. Никурадзе показа-
1 1
тель степени п меняется в пределах -g—=- при изменении
Re от 4-103 до 3-106. Однако в первом приближении показатель степени п может быть принят постоянным в определенном диапазоне чисел Рейнольдса. В расчетах часто
принимают n = Yи ПР°ФИЛЬ скорости задают формулой
![]()
(5-62)
Напряжение трения на стенке при турбулентном движении можно представить также упрощенной опытной зависимостью
![]()
(5-63)
Подставив опытные коэффициенты С = 0,00655 и т =
— — 0,166 в формулу (5-63) и рассматривая частный случай безградиентного течения, из уравнения (5-38) найдем:
Введем в это уравнение число Rej, = ^. Заметим, что
Тогда дифференциальное уравнение для толщины потери импульса запишется в таком виде:
^^-=0,00655 Re’*~0,16G. (5-66)
Предполагая, что на стенке образуется только турбулентный слой, проинтегрируем уравнение (5-66). Тогда получим:
б_
Re** = 0,0153 Re7 .
Отсюда, заменяя Re * и Rex, находим уравнение для толщины потери импульса:
L в_
8" = 0,0153 X7 , (5-67)
или, выразив 5 * в функции числа Re^, найдем:
8** = 0,0153 a Re~7 . (5-68)
Полученное простое решение для толщины потери импульса в турбулентном слое не учитывает влияния сжимаемости и продольного градиента давления. Оно справедливо при М «5:0,5 и ^==0.
Как уже отмечалось, уравнение импульсов (5-38) связывает три неизвестные величины: 8*, 8 и т0. Дополнительные связи, необходимые для решения задачи, устанавливаются опытным путем.
На рис. 5-20 приведена экспериментальная зависимость Н0 = Й (М) для плоской пластины при нулевом градиенте давления. Величина Н0 существенно зависит от числа М; приближенно эту зависимость можно представить следующей формулой:
я„ = я00 (1 + аЩ = Я 00 ( 1+0,3 М°), (5-69)
где для несжимаемой жидкости при нулевом градиенте давления можно принять //00= 1,3-т-1,4, причем меньшее
значение Н00 соответствует большим числам Re. С увеличением числа М несколько уменьшается относительная толщина потери импульса (рис. 5-26)
Влияние градиента давления на параметр Н можно видеть на рис. 5-21, где дана зависимость Н=Н/Н0 от параметра Бури Г.
Отсюда следует, что в зоне умеренных значений параметра Г(—0,015<;Г <0,02)И изменяется на 7°/о- Поэтому при построении решения в отмеченном диапазоне будем учитывать только изменение И0 = Н(Щ.
Для коэффициента сопротивления в турбулентном слое для общего случая была получена формула (5-50). Если отнести т0 к плотности на внешней границе пограничного слоя рх, то формула (5-50) может быть представлена в форме:
"W Т'» “
¦тгКе-
*(С + аГ) =
Рх“0
_1м2
2 о
(5-70)
| *0 | |||||||||||
| s' | * | ||||||||||
|
ri'n | |||||||||||
| —9= | л | ||||||||||
| • | • - |
M |
Рис. 5-20. Влияние числа М на параметр /70.
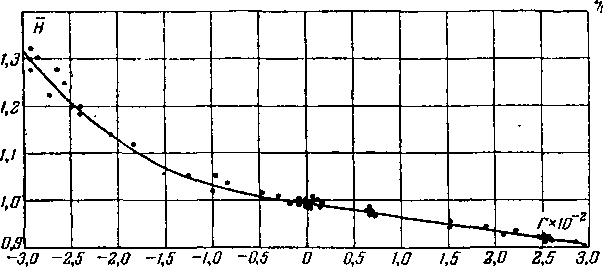
Рис. 5-21. Изменение величины rl в зависимости от параметра
Бури Г.
Подставим (5-69) и (5-70) в интегральное соотношение (5-38). После несложных, но кропотливых преобразований можно получить дифференциальное уравнение относительно параметра Г в следующем виде:
Г' -\-р (а) Г -f- Q (а:) = 0, (5-71)
где х — безразмерная длина обтекаемой поверхности.
Уравнение (5-71) относится к типу линейных и может быть приведено к квадратурам и решено относительно
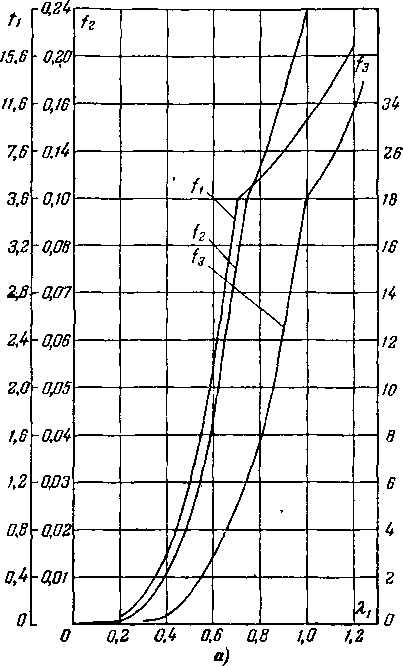
параметра Г. Оно служит для определения параметра Г, исключая область, близкую к точке отрыва.
При равенстве нулю постоянной а и стремлении X к нулю решение переходит в формулу (5-67).
Введя ряд упрощений, получим при небольших градиентах давления (1’> — 0,02) для толщины потери импульса выражение
ГТ**1.2594.17г) 0,2в/е 52 >1,81 ,
2лЖ[6о К Re. (6 — Q ) +
6 =-
Х<*-35 Re°'2(6-X*)
_т0,8
(5-72)
| ft | |
| 15 | о,во |
| 13 | ¦ 0,70 |
| п |
- 0,60 |
| 3,0 |
- 0.50 |
| ю | - ом |
|
5,0 | - о до |
| 3,0 | - 020 |
| 1,0 | - 0,10 |
| 0,8 | ¦ 0,08 |
| 0,6 | ¦ 0.06 |
| 0.4 |
- 0,04 |
| 0,2 |
0.О2 |
| О |
30 26 гг /в /4 ю 6,0 г,о 1,6 1,2 0,8 ОЛ
+ 0,0026 j я392 (6 — Х\ j2-81 dx]
| fz | к |
Т> | ||||
| /! | ||||||
| л | 1/ | / | ||||
| % | f | |||||
| п |
W/ | к | ||||
|
/ | ||||||
| - | / | |||||
| i |
0,2 О,U 0,8 0,8 1,0 1,2 1,Ь
6)
б—чависимость функций <р,, у, и <ра от X,. 17 М. Е. Дейч
и безразмерной скорости в начале турбулентного участка;
a L u
Re =—--число Рейнольдса, определенное по критической
* ~*w
скорости а и кинематической вязкости на стенке.
Вводя обозначения:
^о,35(6-*о)М5;
h
/а = 0,0026 (6 —Я2 f
(5-73)
преобразуем (5-72) к виду:
г=ш* [+1^1“ (5'74)
Функции /2 и fз от Я0 представлены на рис. 5-22,а.
Расчет по формуле (5-74) с использованием расчетных графиков оказывается относительно простым и дает хорошее совпадение с опытными данными.
При больших градиентах давления для толщины потери импульса получим:
0,2 L °о
?,Re*
хв
Здесь
22,35,fi ,2 Л 3 °,10оХ0.
:Яо (6~яо) е ;
?!¦
(5-76)
О
<р2 = 0,0078 Яд'69 (6 — Я2)262 е °;
Г, 131X2
2 U.62
Соответствующие значения ср, ср2 и <р3 приведены на рис. 5-22,6.
В заключение остановимся на существенном различии в свойствах ламинарного и турбулентного слоев. С этой целью в табл. 5-1 приведены основные расчетные формулы
для простейшего случая обтекания плоской стенки (без' градиентное течение) несжимаемой жидкостью.
Сопоставление показывает: 1) профиль скоростей в турбулентном слое более полный, чем в ламинарном; 2) толщина турбулентного слоя растет вдоль стенки значительно быстрее, чем ламинарного, так как в первом случае 5 уве-
6/7
личивается пропорционально л: , а во втором — пропор-ционально я,/2; 3) сравнение местных коэффициентов со-
Таблица 5-1
| Основные харак | Режим пограничного слоя | |
| теристики пограничного слоя |
ламинарный | турбулентный |
| Закон распределения скоростей по сечению слоя |
1 u ~(y\7 «0 | |
| Толщина слоя |
i f VX \2 s-5’83U)= 1 |
S =0,211 [—) *> = ] |
| = 5,83л Re* 2 | = 0,211jcRe7r | |
| Толщина вытеснения | l <Г = 1,72xRex 2 =a0,35 |
1 b*^0y02xRex 7 ^0,095d |
| Толщина потери импульса | l 8« = 0,664jeReJ. 2 5= ^0,11758 | i 8” ==: 0,015* Re7r = ^ 0,071b |
|
Напряжение трения | 1 t0 = 0,332P^ Re^ 2 |
1 = 0,0132p«Q Re* T |
| Местный коэффициент трения | l cf = 0,664 Rej. 2 | 1 cf = 0,0263 Re^ 7 |
|
Коэффициент сопротивления трения | l Cf = 1,328 Re* 2 | l Cf = 0,0307 Re^ 7 |
противления трения показывает, что при одинаковых значениях Re^. сопротивление трения в турбулентном пограничном слое значительновыше, чем в ламинарном. •
Этот весьма важный вывод хорошо подтверждается опытными данными. На рис. 5-23 приведены экспериментальные и расчетные зависимости коэффициентов cf, полученные для турбулентного режима с помощью различных по-луэмпирических формул. Кривые показывают достаточно ' высокую точность формулы, приведенной в табл. 5-1.
OMtn
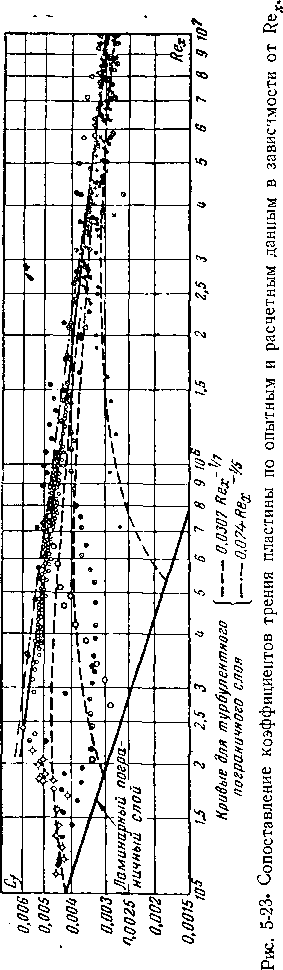
Сравнение cf для ламинарного и турбулентного слоев показывает, что при одинаковом значении 1^= 4-104 коэффициент с/турб в 2 раза превосходит cfmu
(^турв ~ ^,0054, С/лам = = 0,0022). С ростом Re* разность с/турб-с/лам резко увеличивается.
Отсюда следует, что при безотрывном обтекании тела необходимо стремиться к „затягиванию” ламинарного участка слоя, т. е. к сдвигу области перехода в направлении потока.
Обнаруженная разница в сопротивлениях трению при
ламинарном и турбулентном режимах объясняется различ ным механизмом трения в том и другом случаях. Если при ламинарном режиме сопротивление обусловлено поверхностным трением между слоями жидкости (перемешиванием макрочастиц—молекул), то при турбулентном режиме имеют место интенсивные поперечные перемещения микрочастиц. Очевидно, что перемешивание этих частиц связано с потерей значительного количества движения, т. е. с появлением существенных сил трения в потоке.
Многочисленные опыты в соответствии с выводами полуэмпирической теории указывают на еще одно существенное различие в свойствах ламинарного и турбулентного пограничных слоев. Точка отрыва ламинарного слоя при больших числах Re занимает фиксированное положение на обтекаемой поверхности. Точка отрыва турбулентного слоя при одинаковом распределении параметров внешнего потока располагается дальше точки отрыва ламинарного слоя. Другими словами, турбулентный ’слой отрывается позднее ламинарного. Это становится понятным из рассмотрения профилей скорости при одном ¦и другом режимах слоя: кинетическая энергия частиц, движущихся вблизи стенки, при турбулентном режиме значительно больше, чем при ламинарном.
В тех случаях, когда на обтекаемой поверхности существует смешанный пограничный слой, необходимо суммировать сопротивление на ламинарном и турбулентном участках.
Изложенная методика расчета не учитывает влияния начальной турбулентности потока. Для небольших степеней турбулентности уравнение импульсов пограничного слоя для несжимаемой жидкости получено В. А. Врублевской в таком виде:
_' $**
(1+А?о)?г + "^-(2 + Я)=-^- + ?§. (5'77)
и о Р и0
стенке, проведенному в МЭИ. Графики на рис. 5-24 отчетливо показывают влияние ?0 на потери в пограничном слое; так, при Re.,. =
= 2-106 увеличение ?0 от 0 до 5% повышает число Re**, а следовательно, и величину потерь на трение в слое на 70%.
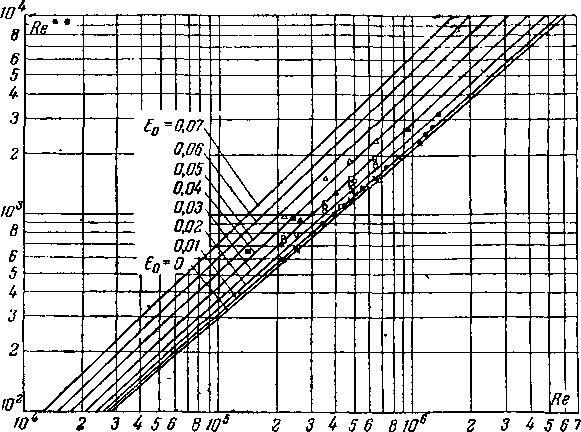
Рис. 5-24. Влияние степени турбулентности на толщину потери импульса в турбулентном пограничном слое.
5-12. ПОГРАНИЧНЫЙ СЛОЙ ПРИ БОЛЬШИХ СКОРОСТЯХ.
ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЕ
Рассмотрим некоторые результаты опытного исследования турбулентного пограничного слоя при больших дозвуковых скоростях при безградиентном течении и докрити-ческих скоростях (М •< М ).
На рис. 5-25 приведены шесть профилей скорости, полученные при постоянном числе Re, равном 2,5-10®, и переменном числе М. Все экспериментальные точки в интервале М = 0,31-т-0,98 образуют одну кривую, которую можно представить зависимостью вида;
Следовательно, при нулевом градиенте давления с изменением числа М профили скорости в координатах у, Я изменяются подобным образом. Кроме того, в указанном диапазоне изменений числа М толщина пограничного слоя при постоянном числе Re изменяется незначительно; поэтому можно говорить не толь- , д
ко о подобии, но и о тождественности профилей скорости. Отсюда можно заключить, что непосредственно на профиль скорости в пограничном слое влияние сжимаемости при М < 1 сказывается незначительно. Таким образом, в первом приближении профиль скорости при М > О можно представить обычной степенной формулой (5-62).
0,9
0,7
0,5
0,4
0,3
0,2
О
| У/5 | Г ' О М=0,ЗЮ Л 0,54-5 х 0,610 « 0,794 • 0,900 * М=0,980 | V о | ||
| • S * о • • . л | ||||
| 0 |
||||
| * я • | ||||
| ( | 1 ¦ о - | |||
| jf & jifi | ||||
|
4 Г | (Г |
|||
| «1 хо*« |
N | и/и0 | ||
0,9 КО
0,5 0,6 0,7 0,8
Рис. 5-25. Влияние числа М на профиль скорости в турбулентном погра
0,8
0,6
Формула (5-62) не является, конечно, единственной. Любая зависимость, удовлетворительно аппроксимирующая профиль скорости в пограничном слое несжимаемой жидкости, может ,быть распространена и на течение сжимаемой жидкости. Пределы такой экстраполяции не ограничиваются, по-видимому, звуковой скоростью и могут быть распространены и на сверхзвуковые скорости.
0,1
ничном слое.
Дальнейшая обработка профилей скорости дает возможность вычислить значения интегральных толщин 8 ,
о и построить кривые их изменения в зависимости от числа М (рис. 5-26). Разброс экспериментальных точек в области околозвуковых скоростей объясняется возникновением конфузорного течения. Кривые для околозвуковых скоростей проведены через точки, полученные при минимальном градиенте давления; поэтому в области звуковых и сверхзвуковых скоростей основная масса точек располагается под кривыми. Разброс точек, обнаруживаемый в области дозвуковых скоростей, объясняется тем, что здесь нанесены точки, относящиеся к различным числам Re.
Полученная картина находится в полном соответствии с теоретическими результатами. Увеличение числа М при-
мм
о,з&
0,30 0,26 0,22 0,18 0,14 0,10
| 5** | 1 гшт/гт* | ||||||||||
| А Я ' " | о | О О | "'% Г | *0» | -JL | UU |
/”00' | ||||
| • | > | • |
о • | «г |
d | ь° | - | ||||
| • | • |
• | |||||||||
|
/ F* | Яе=(2+4)-Ю6 |
• 1 • | • | ||||||||
| • |
• | ' т |
|||||||||
|
М |
|||||||||||
1,1
1,0
0,3
0,8
0,7
Рнс. 5-26. Влияние числа М на толщину потери импульса.
водит к падению толщины потери импульса и к росту толщины вытеснения 5*. Такое поведение кривых при одинаковых профилях скорости обусловлено изменением плотности поперек пограничного слоя, причем противоположное влияние этого изменения на толщины 8 и 8 объясняется тем, что подынтегральные функции, через которые выра-жаются толщины о,5, по-разному реагируют на изменение плотности.
Для приближенной количественной оценки влияния сжимаемости на толщину потери импульса 8 на рис. 5-26
8**
приведено изменение относительной толщины —= 8" в
йоо
зависимости от М при нулевом градиенте давления. С приближением к звуковой скорости уменьшение толщины потери импульса составляет около 15°/0.
Независимость профиля скорости от числа М дает основание считать число Re основным параметром, определяющим профиль скорости при отсутствии градиента давления, и распространить результаты многочисленных экспериментов по определению его влияния в несжимаемой жидкости на течение сжимаемой жидкости.
|
УР | • О | г ¦ ¦¦ 1 Re--=0,6/ Юв 1,08 10 е 2,00 Юв 3,50 10 6 /. пп | л 8 V * | |
|
& А | в | |||
| Ж | Re-5,1 | i7 /U 2 Ю6 | в • О | |
|
ГГ в •v | ||||
|
М=0,, | 15 |
i « 4v •о |
||
| •? |
I ? | |||
| .4* S? • • |
||||
| • • о • | Ў т * |
|||
| • • л 1 1 • А О* | ¦$* 2 А | a/u0 | ||
0,6 0,7 0,8 0,3 1,0
Рис. 5-27. Влияние числа Re на профиль скорости в турбулентном пограничном слое.
1,0
0,9
0,8
0,7
0,6
0,5
а Л о,э о,г о,/
о 0,5
На рис. 5-27 приведены шесть профилей скорости, полученные при изменении числа Re и постоянном числе М. Увеличение числа Re от 0,61*10“ до 1,08-10“ приводит к характерному изменению профиля скорости. Дальнейшее увеличение числа Re не вызывает заметного изменения профиля скорости. Другими словами, начиная с величины
Re ж 10е, профили скорости могут быть выражены общей зависимостью.
Исследование влияния числа Re на интегральные толщины 8* и 5** показало, что с ростом Re, как и в случае несжимаемой жидкости, эти величины уменьшаются. В области малых значений Re изменение §’* оказывается довольно заметным. С увеличением числа Re уменьшение толщины 8*’ происходит менее интенсивно. Аналогичным образом меняются и толщины вытеснения.
Таким образом, влияние числа Re при больших скоростях на турбулентный пограничный слой с качественной стороны оказывается того же порядка, что и в потоках несжимаемой жидкости.
Для исследования вопроса о влиянии числа М при наличии градиента давления были сняты профили скорости в диффузорной области (рис. 5-28,а) и при конфузорном течении (рис. 5-28,6). Как видно из приведенных кривых, все экспериментальные точки независимо от числа М образуют практически одну кривую. Этот факт еще раз подтверждает сделанный ранее вывод о том, что при дозвуковых скоростях изменение числа М не приводит к заметным изменениям профилей скорости. Следовательно, основным фактором, определяющим течение в пограничном слое сжимаемой жидкости, является продольный градиент давления.
Результаты исследования показывают, что влияние сжимаемости на структуру турбулентного пограничного слоя является косвенным. При изменении числа М меняется распределение давлений вдоль обтекаемой поверхности. С ростом числа М абсолютные значения градиентов давления возрастают. В соответствии с этим меняются основные характеристики слоя. В конфузорном течении 8** уменьшается, а в диффузорном—возрастает.
Изменение продольного градиента давления от положительного до отрицательного значения приводит к существенной деформации профилей скорости. Это отчетливо видно из рис. 5-29, где изображены профили скоростей, полученные в диффузорном канале при различных градиентах давления.
На рис. 5-30 приведена кривая изменения толщины потери импульса в функции параметра Г, полученная из эксперимента. Чтобы исключить влияние сжимаемости, тол-
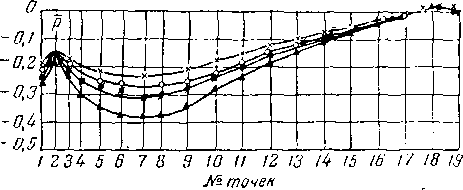
0J
D
| у/в | ¦ “.....“П о А |
- м=о,с о,ь 0,h 0,5 | г --- 756 70 | 1 с | ||
|
X * | ’SO | |||||
| • |
M=0,t | Э | ||||
| ? * Щ %° | ||||||
| V X *> ? | ||||||
| h f* f I* ё | ||||||
| 1 .... ^ А | ||||||
| О JP |
/ | |||||
| ¦ °хг - | ||||||
| о | О |
о о %{!* *.Г |
& |
u/uD |
Рис. 5-28. Влияние числа М на профиль скорости в турбулентном пограничном слое. а —»профиль скорости в диффузорной области, Re=I,5*lO*;
1,0 0,9 0,3 0,7'
0,6 0,5 ОЛ 0,3
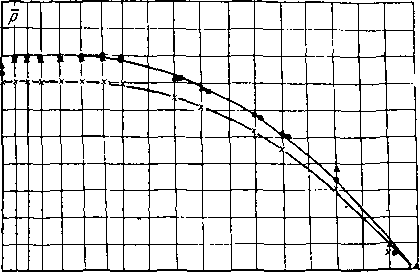
1 23 4 5 6 7 8 9 10 И 12 13 lb 15 16 17 18 19 Ш точвк
7,0 0,9
0.8
0,7 0,6 0,5 0,4 0,3 0,2 0.1 О
| у/5 | 1 г ' х м^о,Ш • П RRD | |||||
| А | о Мб \ | 4 л | ||||
| X Л |
||||||
| -^ | А | |||||
|
9 А 9 | ||||||
|
А А 9 |
||||||
| -?" * i | ||||||
| \ / | ||||||
| > |
{ X» Г | |||||
|
Г <• | ||||||
| - | »-* | Фо | ||||
0,3 О л 0,5 0,6 0,7 0,8 0,9 КО
6)
Рис. 5-28.
б — профиль скорости в конфузорной области, Re=2'I0.
и о 0,3
о,в 0,7
б,в
i 7
0,5
ОА
а} 05 Т~6 0J 0J3 Жз То
а
щина 6" была отнесена К соответствующей толщине 6** для безградиентного течения при той же скорости внешнего потока. Все точки группируются вокруг одной кривой.
Из кривой следует, что в данном случае 8" является функцией одного параметра Г. Следовательно, когда распределение скорости на внешней границе пограничного
мм
| У | ||||
|
W/. ////У. | ¦ |
|||
| ? | -X, * J | |||
| ..... | ||||
|
X | ||||
| - -//] | ||||
| i |
¦/// ГА Ilf | |||
| / / | ||||
| /- | 1/ 2 * | |||
| / | 4 J | i - | ||
| Л 7 У | ||||
|
| — | 1 |
|||
0,1 О,г 0,3 0,Ь 0,5 0,6 Пг7 О,в 0,9 ш
Рис. 5-29. Профили скорости в диффузоре при различных градиентах давления.
/—8"=0.61 мм; S*=l,095 мм; М=0,9б0; Я=2,4; Я0=1,65; г~г**=0,552 мм; 5*= =0,765 мм; М=0,548; //=1,57; Н0=\ 4; 3—8**=0,384 мм; 5*=0,52 мм; М=0,54; Я= =1,52; й0=1,4; 4 — 5**=0,37 мм; S*=0,638 мм; М=0,985; Я=2.2; Н,~ 1.7.
слоя близко к линейному, расчет по однопараметрическому методу физически обоснован. Отсутствие экспериментальных данных, относящихся к другим значениям второй производной, не позволяет сделать более общего вывода.
Опытные данные, характеризующие влияние начальной турбулентности на структуру пограничного слоя,^ показаны на рис. 5-31. С увеличением Е0 возрастает полнота профиля скорости. Однако наполнение профиля существенно
|
г___ | ** о | ||||||||||
| 0^ | |||||||||||
|
\о | О | ||||||||||
|
о\ | tap | ||||||||||
|
o'» | |||||||||||
|
} | -и ~ ю |
-зоо -гоо -юо о юо гоо зоо
Рис. 5-30. Зависимость относительной толщины потери импульса от параметра Г.
зависит от знака и величины градиента скорости внешнего потока. Наибольшее влияние Е0 оказывав в диффу-зорном течении, что подтверждают графики изменения 5” вдоль плоской стенки при различных градиентах давления (рис. 5-32). Наименее чувствительным к изменению Е0 является конфузорный поток
С возрастанием числа Рейнольдса влияние Ед уменьшается (рис. 5-32). Аналогичный результат получен и при различных числах М; с увеличением М расхождение кривых уменьшается, в особенности при М, близких к единице.
Отметим, что в связи с увеличивающейся полнотой
ь*
профиля скорости в слое параметр Н = ^ заметно сни-
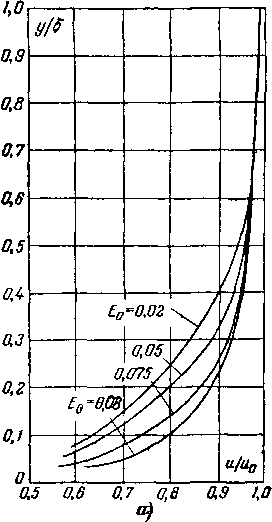
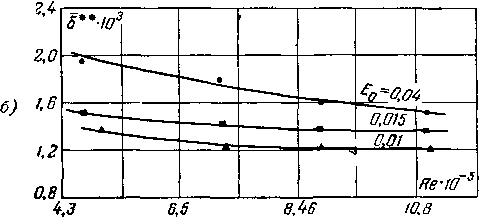
Рис. 5-31. Влияние начальной турбулентности.
а — на профили скорости в турбулентном пограничном слое; б—на толщину потерн импульса прн различных градиентах давления.
жается с ростом степени турбулентности; в зависимости от знака продольного градиента давления это снижение составляет 15 — 20 °/0.
Особенно велико влияние начальной турбулентности при отрывном обтекании поверхности. В этом случае увеличение Е0 приводит к резкому смещению точки отрыва по потоку и к улучшению обтекания поверхности.
3.5 -----------
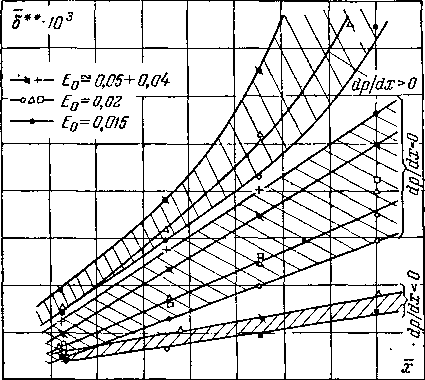
ол ___________________
П.2 0.3 ОА 0.5 0.8 ОЛ 0.8 0.3 КО /,/
Рис. 5-32. Влияние начальной турбулентности на толщину потери импульса при градиентном течении.
3,2
2,8 2А г,о
КБ К г 0,8
Приведенные данные показывают, что при расчете турбулентного пограничного слоя необходимо учитывать влияние начальной турбулентности. Заметные расхождения между опытными и расчетными [по формуле (5-70)] значениями о” отмечаются при Е0 Зз 3 °/0.
Рассмотрим некоторые свойства пограничного слоя при околозвуковых скоростях75. „
Если скорость набегающего потока Мот будет больше критического значения М., то у поверхности обтекаемого тела образуется область сверхзвуковых скоростей.
Область сверхзвуковых скоростей имеет ограниченную протяженность в направлении, нормальном к обтекаемой поверхности. В направлении течения (вдоль обтекаемой поверхности) область сверхзвуковых скоростей также” ограничена. К этому заключению легко прийти, вспоминая, что на некотором удалении за телом скорость должна быть дозвуковой, так как скорость невозмущенного потока (перед телом) — дозвуковая.
Таким образом, зоны сверхзвуковых скоростей, появляющиеся при имеют местный характер. В мест
ной сверхзвуковой области течение газа вначале ускоряется, а затем тормозится. Однако торможение сверхзвуко-
мч
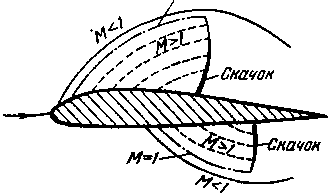
Рис. 5-33. Схема образования скачка уплотнения в местной сверхзвуковой зоне.
вого потока, как правило, происходит с образованием скачков. Благодаря большим ускорениям в зоне сверхзвуковых скоростей газ оказывается значительно перерасши-ренным, т. е. его давление падает значительно ниже давления внешней среды. Это перерасширение сверхзвукового течения погашается скачком уплотнения.
Как выше уже отмечалось, скорости при удалении от тела меняются по величине и направлению (возмущение потока в направлении от тела уменьшается). Благодаря этому образующиеся скачки уплотнения будут криволинейными с переменной вдоль линии скачка интенсивностью: за скачком поток становится вихревым. Образующиеся скачки уплотнения замыкают область сверхзвуковых скоростей. Передней ее границей является линия перехода (линия М{. = 1). Для идеальной жидкости замыкающей поверхностью служит поверхность обтекаемого тела (рис. 5-33).
В реальном случае вязкого газа расположение и протяженность местной сверхзвуковой зоны, а также структура скачков изменяются. Механизм взаимодействия скачков с пограничным слоем составляет важную часть проблемы сопротивления тел при околозвуковых скоростях.
| \У хо<а | ||
| ( <«? « |
||
| 1 |
J | щ |
| 1 | ||
| .—¦ |
||
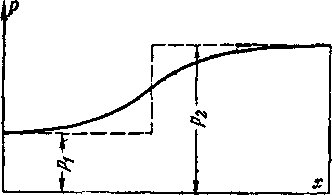
Рис. 5-34. Схема взаимодействия прямого скачка и пограничною слоя.
Скачки уплотнения в местной сверхзвуковой зоне создают большие градиенты давления, которые распространяются и в область пограничного слоя. Возмущения, возникающие в пограничном слое, распространяются против течения и по течению и влияют на поле потока у обтекаемой поверхности.
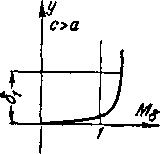
Рассмотрим вначале простейший случай, когда в сверхзвуковой зоне образуется один прямой скачок76 (рис. 5-34).
В пограничном слое скорости меняются от нуля на стенке до сверхзвукового значения во внешнем потоке. Следовательно, в пределах слоя располагается линия перехода (М =1), которая делит область пограничного слоя на дозвуковую и сверхзвуковую части. Заметим, что в турбулентном пограничном слое дозвуковая часть имеет относительно меньшую толщину, чем в ламинарном. Очевидно, что повышение давлений распространяется через дозвуковую часть слоя навстречу течению.
Возрастание давлений в зоне скачка может привести к появлению отрыва. При турбулентном режиме интенсивность скачка, вызывающего отрыв, должна быть более высокой, ибо, как было показано выше, турбулентный слой всегда отрывается позднее. Заметим, что так как в дозвуковой части слоя повышение давления распространяется против течения, то точка отрыва, как правило, располагается перед скачком.
Так как интенсивность скачка в направлении от стенки меняется (в соответствии с изменением скоростей), то в пограничном слое образуется поперечный градиент давления и основное условие, принятое в расчетах слоя
^-^- = 0^, в области скачка не соблюдается. Возмущение, распространяющееся в дозвуковой части слоя, приводит к нарушению этого условия и перед скачком.
Отсюда заключаем, что режим течения в пограничном слое должен оказывать существенное влияние на положение скачка в местной сверхзвуковой зоне, на структуру и интенсивность окачка. Это влияние объясняется различием в профиле скоростей ламинарного и турбулентного слоев Следует, однако, учитывать, что распределение скоростей в пограничном слое зависит не только от режима течения, но и от характера изменения скорости внешнего потока и, следовательно, от кривизны обтекаемой поверхности.
Опытные исследования .подтверждают возникновение различных по структуре скачков в ламинарном и турбулентном пограничных слоях (рис. 5-35).
При ламинарном слое местные скачки имеют, как правило, Я-образную форму; такой скачок состоит из наклонного криволинейного скачка, сливающегося с более мощным и более протяженным окачком небольшой кривизны, замыкающим сверхзвуковую зону. Появление криволинейного скачка можно объяснить следующим образом. Повышение давления, распространяясь в дозвуковой части слоя, вызывает заметное увеличение его толщины перед скачком. Линии тока в пограничном слое отклоняются от поверхности тела; в результате возникает система слабых волн уплотнения, которые и обра-скачками восстанавливается нормальное обтекание поверхности дозвуковым потоком. В дифф>зорном течении за скачками отрыв обычно развивается и переходит в кормовую область за телом.
Ламинарный слой
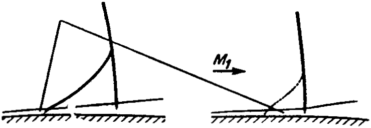
ТурБулвнтный слой
М,
'77777777777777777
М]—const
Рис. 5-35. Схемы скачков (а) и спектр течения (б) в местной сверхзвуковой зоне при ламинарном и турбулентном режимах пограничного слоя.
зуют наклонный скачок. С увеличением числа Re (при Mi = const) по мере выравнивания поля скоростей в пограничном слое кривизна линий тока перед скачком уменьшается и при развившемся турбулентном профиле скоростей первый скачок исчезает; остается один, но бо-' лее мощный'скачок небольшой кривизны.
Отрыв лотока в местной сверхзвуковой зоне происходит не во всех случаях. Иногда в зависимости от распределения скорости во внешнем течении отрыв имеет локальный характер и на некотором расстоянии за
На рис. 5-36 .приведена схема образования отрыва в сверхзвуковой области. Точка перехода ламинарного слоя в турбулентный (точка Т), как правило, располагается вблизи точки отрыва s.
Перейдем теперь .к краткому рассмотрению схемы взаимодействия .пограничного слоя при сверхзвуковых скоростях с волнами разрежения и скачками уплотнения. Так как в реальном сверхзвуковом течении всегда образуются скачки уплотнения и волны разрежения, то одной из важных задач теории пограничного слоя при Моо>1 является изучение взаимодействия скачков и волн с пограничным слоем.
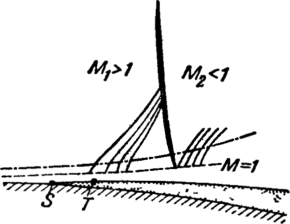
Рис 5-36 Схема отрыва пограничного слоя перед скачком уплотнения
Опытные данные позволяют заключить, что условия взаимодействия скачка с пограничным слоем могут быть различными в зависимости от интенсивности скачка, распределения скоростей внешнего потока и режима течения в слое.
Принципиальные схемы взаимодействия скачков и волн разрежения с пограничным слоем приведены на рис 5-37. При небольшой интенсивности . скачка
(рис 5-37,а) перед ним вблизи точки его ладейия происходит «разбухание» слоя.
В результате перед скачком образуется система слабых волн уплотнения, создающих отраженный скачок CD. Обтекание утолщенной дозвуковой части слоя сопровождается образованием слабой волны разрежения и второго отраженного скачка FE. При значительной интенсивности падающего окачка (рис. 5-37,6) повышение давлений перед скачком вблизи точки падения может привести к местному отрыву потока.
При падении на стенку волны разрежения толщина пограничного слоя перед волной может убывать.
Таким образом, мы -видим, что действительные схемы отражения скачков и волн разрежения от стенки, обтекаемой вязкой жидкостью, существенно отличаются от схем, рассмотренных в гл. 3 и 4, для идеальной жидкости. Основное отличие заключается в том, что скачки (волны разрежения) через дозвуковую часть слоя изменяют поле потока перед точкой падения, а деформируемый при этом пограничный слой создает новые волновые образования. Однако основное свойство твердой стенки, отражающей скачки (волны) с тем же знаком, сохраняется и в вязком потоке.
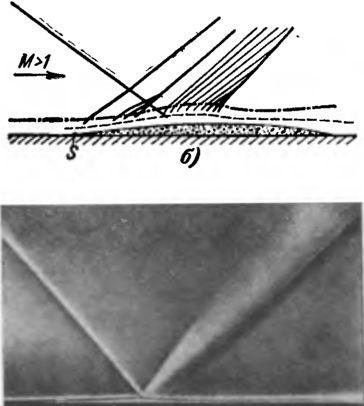
Рис. 5-37. Схемы взаимодействия скачков с пограничным слоем при сверхзвуковых скоростях.
6)
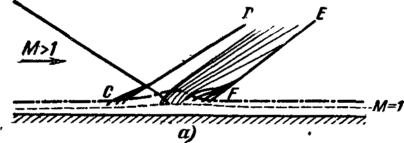
5-13. СОПРОТИВЛЕНИЕ ТЕЛ ПРИ ДОЗВУКОВЫХ И СВЕРХЗВУКОВЫХ СКОРОСТЯХ
На тело, обтекаемое потоком газа, действуют силы давления и касательные силы трения. Результирующая этих сил является полной аэродинамической силой. При изучении ^плоского обтекания аэродинамическую силу принято представлять двумя 'составляющими: Рх и Ру (рис. 5-38). Как известно1, составляющую Рх, направление которой совпадает с направлением скорости набегающего потока, называют силой лобового сопротивления, а составляющую Ру, нормальную
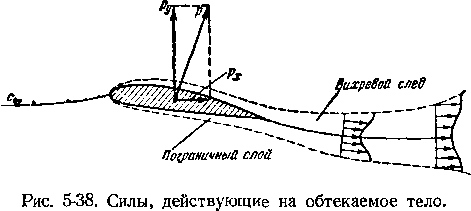
к вектору скорости набегающего .потока, принято называть 'подъемной силой или силой Жуковского.
Имея в виду происхождение силы Рх, лобовое сопротивление подразделяют на сопротивление трения и сопротивление давления. Такое разделение, несмотря на некоторую условность, практически весьма удобно при расчете сопротивления.
Тело, помещенное в поток, создает возмущение, в результате которого в области, прилегающей к телу, меняются параметры течения. Распределение давлений у поверхности тела зависит от его формы и ориентировки в потоке, а также от скорости невозмущенного потока. Распределение сил трения на поверхности тела также зависит от этих факторов.
Распределение давлений >по поверхности тела характеризуется коэффициентом давления. Рассмотрим распределение давлений по крыловым профилям различной формы при различных небольших углах атаки (рис. 5-39) для небольших скоростей77. На верхней и нижней поверхностях вблизи носика профиля происходит интенсивное ускорение потока с соответствующим снижением давления. Эти участки ¦ профиля являются 'конфузорньгми. Снижение давления на верхней поверхности профиля
происходит более интенсивно, чем на нижней. За точками минимума «а нижней и верхней поверхностях поток замедляется. Эта область течения у крыла является диффузорной. Заметим, что диффузорный участок на верхней поверхности характеризуется более высокими значениями градиента давления. На задней кромке профиля, где происходит слияние струй, сбегающих с верхней и нижней поверхностей профиля, .полное давление не восстанавливается, та'К как в пограничном слое имеют место необратимые потери (рис. 5-38).
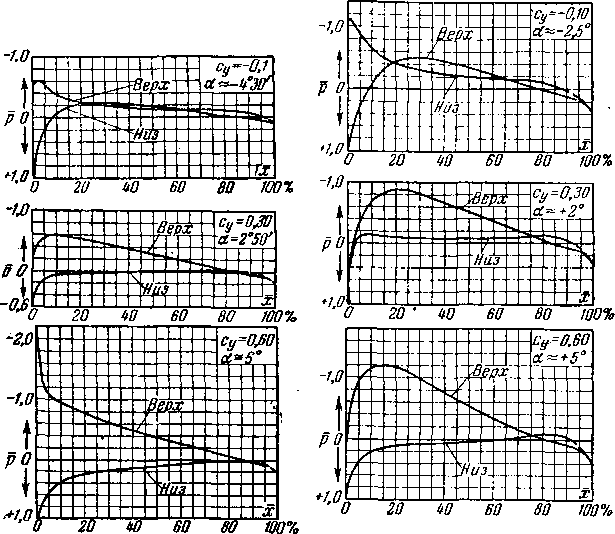
![]()
Рис. 5-39. Распределение давлений по двум профилям различной толщины при разных углах атаки для небольших дозвуковых скоростей. а — угол атаки; су — коэффициент подъемной силы»
При увеличени угла атаки картина давлений на профиле существенно меняется. Значительные диффузор-ные участки появляются на нижней поверхности у носика.
Как мы видели, лри сходе с задней кромки профиля образуется вихревой след, насыщенный вихрями, зарождающимися в пограничном слое. Структура вихревого следа меняется с удалением от профиля. Вихри, зарождающиеся в пограничном слое, развиваются при срыве с профиля и затем на значительном расстоянии за телом затухают в результате взаимодействия с внешним лото-ком. При этом энергия вихрей преобразуется в тепло. Образование вихрей приводит к снижению давления в области задней кромки и за профилем в следе.
При известном распределении, давления по контуру крыла можно найти проекцию сил давления на направление вектора скорости с .
Легко видеть, что
![]()
где ds — элемент поверхности профиля.
Сила Р'х, обусловленная разностью давлений в точках
обтекаёмого тела и направленная против его движения, является силой сопротивления давлений. Кроме силы Р'х , на профиль действует результирующая касательных сил тре-
![]()
Таким образом, полное лобовое сопротивление тела в плоском потоке является суммой сопротивления давления и сопротивления трения: чину — вязкость жидкости. Профильным сопротивлением называют сопротивление цилиндрического крыла при его безотрывном обтекании безграничным плоским потоком.
![]()
Необходимо особо подчеркнуть, что сопротивление давления и сопротивление трения имеют одну и ту же при-
Для оценки силового взаимодействия между потоком и обтекаемым телом вводятся безразмерные коэффициенты сил, которые называются аэродинамическими коэффициентами.
Так, сопротивление тела характеризуется коэффициентом лобового сопротивления
2Рх 2Рх
°Х Роо4 Ъл2ооРсор
где F — характерная площадь78 тела;
р — статическое давление невозмущенного потока.
Коэффициентом подъемной силы по аналогии называют величину
_ 2РУ __ 2РУ
У Роо4/ кМ^оо F
Как уже указывалось, силы, действующие на обтекаемое тело, а следовательно, и аэродинамические коэффициенты сх и Су зависят' от формы тела, режима его обтекания и ориентировки тела в потоке. При малых скоростях, когда сжимаемость практически не сказывается, основное влияние на коэффициент сопротивления оказывают форма тела, угол атаки и число Re. Существование такой зависимости, подтверждаемое многочисленными опытами, вытекает из физической природы сопротивления давления и Сопротивления трения.
Действительно, .в зависимости Ьт формы тела меняется характер возмущения, создаваемого телом в потоке. При этом изменяются распределение параметров течения по обводу тела и, следовательно, обе составляющие силы Рх. Сопротивление трения меняется в связи с изменением структуры пограничного слоя и режима течения в нем.
Аналогичная перестройка спектра обтекания происходит при изменении ориентировки тела в потоке. В этом случае точно так же меняются полное сопротивление тела и его составляющие. Отсюда также следует, что в полном балансе сопротивлений тела удельный вес сопротивления давления и сопротивления трения может быть различным в зависимости от указанных ¦параметров. Так, профили хорошо обтекаемой формы при малых скоростях имеют сравнительно небольшое профильное сопротивление, причем основным является сопротивление трения. При увеличении относительной толщины профиля *и угла атаки роль сопротивления давления увеличивается. Сопротивление трения вначале меняется мало, а затем снижается. Так же как и полная сила лобового сопротивления, коэффициент сопротивления может быть представлен в виде двух слагаемых:
с =с -4-с
X хд, I хтр’
где схл — коэффициент сопротивления давления;
°хтр — коэффициент сопротивления трения.
С увеличением толщины профиля положительные градиенты давления на кормовой части профиля увеличиваются и точка отрыва смещается против потока. По этой причине увеличивается сопротивление- давления. Так как при этом величина поверхности трения сокращается, то с „ снижается.
хтр
С ростом числа Re^ для хорошо обтекаемого профиля схд незначительно убывает, так как уменьшаются толщина пограничного слоя и зона срыва. Вместе с тем при возрастании Re^ уменьшается и коэффициент трения (см. предыдущие параграфы). При оценке влияния формы тела и числа Re^ иногда следует учитывать, что пограничный слой оказывает влияние на внешний поток: линии тока внешнего течения вытесняются пограничным слоем. Подробное исследование позволяет установить, что распределение давлений по контуру профиля в потоке вязкой жидкости совпадает с распределением давлений по обводу некоторого фиктивного тела (полученного из профиля путем утолщения его на величину толщины вытеснения §*), обтекаемого идеальной жидкостью. Отсюда следует, что структура пограничного слоя определяется внешним потоком, а с другой стороны, пограничный слой может оказывать обратное влияние на внешний поток. Заметим, что обратное влияние слоя оказывается особенно существенным у задней кромки профиля, где толщина слоя имеет наибольшее значение. Толщина и распределение скоростей в пограничном слое у задней кромки в значительной степени влияют на профильное сопротивление.
Число ReOT влияет на отрыв потока. Отрыв потока может появиться при больших углах атаки, когда положительные градиенты давления в диффузорных областях достигают больших значений. Увеличение числа Re^, приводящее к турбулизадии слоя, может резко уменьшить коэффициент профильного сопротивления при больших углах атаки, так как отрыв перемещается к задней кромке профиля и сопротивление давления снижается. Увеличение числа Re^ при смешанном безотрывном обтекании смещает область перехода против потока и может привести к возрастанию сопротивления трения.
При больших значениях Мда набегающего потока на профильное сопротивление влияет сжимаемость. При безотрывном обтекании тонких тел хорошо обтекаемой формы точка перехода смещается по потоку и коэффициент сопротивления несколько уменьшается. При появлении на контуре тела отрыва увеличение смещает точку отрыва против потока, чем ухудшает обтекаемость тела. Следует заметить, что, помимо этого, с ростом Мм возрастает интенсивность вихревого движения в кормовомследе тела.
Заметное увеличение коэффициента сопротивления обнаруживается при околозвуковых скоростях. В этом случае коэффициент сопротивления в функции числа М<х> резко возрастает и в зависимости от формы тела может в несколько раз превысить значение сх при Ранее было показано, что скачки часто 'приводят к отрыву -потока, что вызывает еще 'более резкое возрастание сопротивления.
Характер распределения давлений по профилю при околозвуковых скоростях можно видеть на рис. 5-40,а (зона сверхзвуковых скоростей заштрихована). Здесь отчетливо заметны .место расположения скачков и повышение давлений в скачках. На рис. 5-40,6 приведена кривая коэффициентов профильного сопротивления в этой зоне скоростей для крылового профиля.
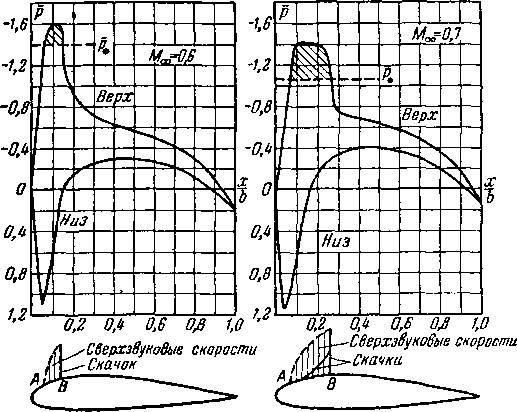
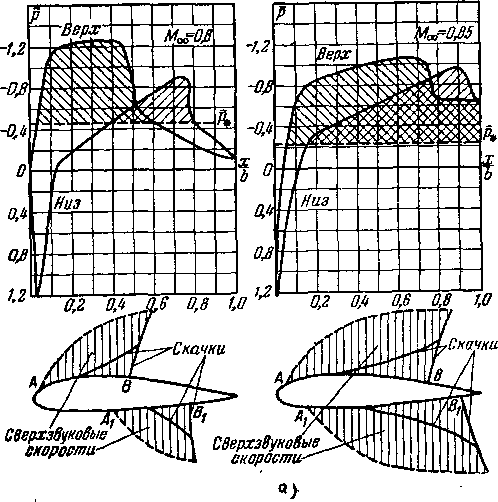
Рис. 5-40. Распределение давлений по профилю при околозвуковых скоростях (а) и коэффициенты сопротивления профиля в зависимости от числа Мм (б).
Отмеченные выше особенности обтекания тел при околозвуковых скоростях характеризуют специфическое влияние сжимаемости Изложенное показывает, что возрастание коэффициента профильного сопротивления при Моо>М объясняется увеличением сопротивления давления. При развитой системе скачков на профиле и отрыве потока доля сопротивления трения невелика и ею изменение не может объяснить столь значительное возрастание сх. Заметим, что при Моо>М может происходить резкое уменьшение коэффициента подъемной силы су; изменение су также обусловлено перераспределением давлений на профиле и наступает обычно при больших числах М», чем те, при которых отмечается возрастание сх.
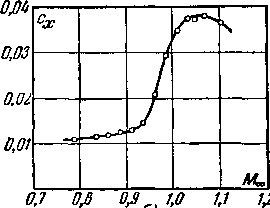
Появление звуковых скоростей в точках профиля можно установить по картине распределения давлений. Коэффициент давления в этих точках принимает значение, определяемое то формуле (3-17).
Из предыдущего следует, что значение М зависит не только от формы тела, но и от ориентировки тела в потоке, т. е. от угла атаки.
При сверхзвуковых скоростях набегающего потока' сопротивление давления в основном определяется волновым сопротивлением. Расположение и интенсивность скачков и волн разрежения зависят от формы обтекаемого тела, расположения тела в потоке и числа Моо.
Рассмотрим обтекание ромбовидного профиля при Моо>1 (рис. 5-41). Зная геометрические размеры профиля, используя формулы, приведенные в гл. 3 и 4, можно расчетным путем построить картину обтекания такого профиля; найти углы и интенсивность головного и хвостового скачков ABC и AiBxC1 и волн разрежения
DEF и D\EXFX. Тогда мы определим давления в областях II и III. Найдя проекцию результирующей силы давления на направление невозмущенного потока, убеждаемся в существовании силы сопротивления, обусловленной изменением давлений в скачках и волнах разрежения. Заметим, что в отличие от дозвуковых скоростей эту часть сопротивления давления лри околозву-
? F
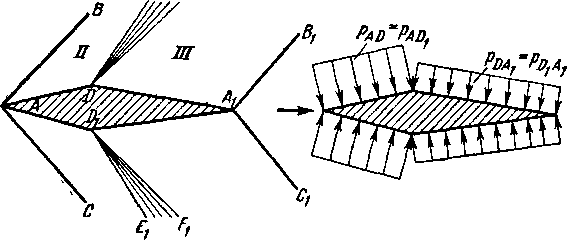
Рис. 5-41. Спектр обтекания ромбовидного профиля потоком сверхзвуковых скоростей.
ковых и сверхзвуковых скоростях (волновое со,противление) выделяют в самостоятельную категорию. Коэффициент профильного сопротивления представляется в такой форме:
с с п —I— с
х х тр I х в >
где схв — коэффициент волнового сопротивления тела.
5-14. СОПРОТИВЛЕНИЕ ПЛОХО ОБТЕКАЕМЫХ ТЕЛ
В ПОТОКЕ ГАЗА
Плохо обтекаемыми будем называть такие тела, которые в любом положении обтекаются с отрывом потока. Для плохо обтекаемых тел, даже при малых скоростях, значительную часть полного сопротивления составляет сопротивление давления.
Специфические особенности спектра отрывного обтекания можно проследить на примере шара или цилиндра.
На рис. 5-42 приведены кривые распределения давлений по обводу шара при М = 0 (несжимаемая жидкость) для различных Чисел Рейнольдса. На участке от передней критической точки до точки М давление вдоль обвода шара резко снижается (конфузорная область), а затем за миделевым сечением наблюдается рост давления (диффу-зорная область). В некоторой точке S происходит отрыв слоя; за линией отрыва давление меняется слабо.
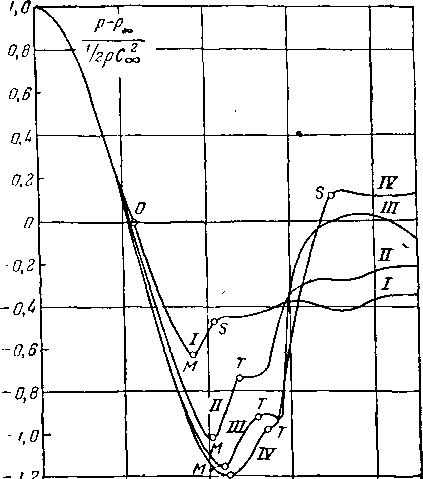
Рис. 5-42. Распределение давлений по обводу шара при разных числах Рейнольдса.
/ —Re=157 200; ех=0,471; II —Re=251J300; сх=0,№; III —Пе=
=238 500; с*=0,151; IV — Re=424 500; <7^=0,143.
Lit_I__1--1--j-- ,
О 20 ко ВО 80 ЮО 120 /4 О !ВО град
При рассматриваемых скоростях 0) значительнее
влияние на распределение давлений оказывает число Рейнольдса.' Можно отметить, что с ростом Re^ давление в точке М уменьшается, а в точке 5 — растет. Характерно также смещение точек М и S по потоку.
Многочисленные опыты подтверждают существование зависимости коэффициента сопротивления шара (цилиндра)
от числа Re^. На рис. 5-43 приведены соответствующие графики. Здесь могут быть отмечены пять характерных областей изменения сх. При Re^^2-103-н 3-103 сх уменьшается79 с ростом Re^ и особенно интенсивно в зоне малых Re^-c^ 100. На участке Re00 = 2-103 -н 2-104 коэффициент сопротивления несколько возрастает (область III), а затем в интервале Reoo = 2- 104-f-2-105 сх сохраняется постоянным (область IV). Вслед за тем в узком диапазоне изменений Re^^2 • 105 н- 4 • 105 (4,5 • 105)сх кризисным образом уменьшается (область V). При Reoo>4,5-105 отмечается некоторое увеличение сх, после чего сх принимает практически постоянное значение.
Опыты показывают, что переход из одной области в другую сопровождается изменением спектра обтекания шара (рис. 5-43). При малых Re^ 100 основную роль играет сопротивление трения, причем резкое уменьшение сх с ростом числа Рейнольдса в этой области подтверждает отсутствие „квадратичной* зависимости между силой сопротивления и скоростью с^. Образование отрыва в кормовой части вызывает далее медленное падение сх с ростом Re^. Область III характеризуется слабым возрастанием сх, что объясняется интенсификацией вихревого движения в кормовой области. В этой области сопротивление трения в пограничном слое невелико. Основную роль играет сопротивление давления.
Здесь, как и в области IV, на линии отрыва слой ламинарный. Как известйо, положение точки отрыва ламинарного слоя не зависит от числа Рейнольдса. Следовательно, при некотором значении Re^^s 105-т-2-104 линия отрыва занимает фиксированное положение на поверхности шара (цилиндра) и дальнейшее возрастание Re^ не приводит к изменению положения линии S.
Область IV, соответствующую постоянному значению сх, называют областью „автомодельности* по числу Рейнольдса. Однако и в этом интервале изменений Re^ происходит перестройка спектра обтекания шара. Отрывакг
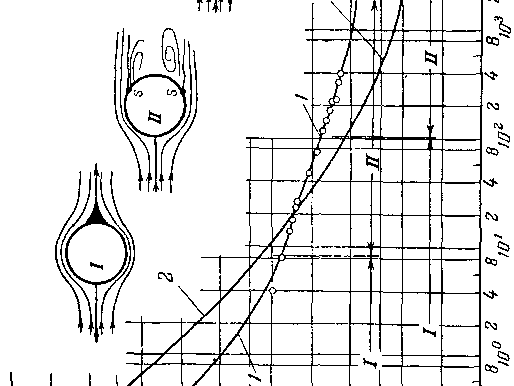
Рис. 5-43 Схемы обтекания и коэффициенты сопротивления шара и цилиндра в зависимости от числа Рейнольдса.
1—Для цилиндра; 2— для шара.
щийся в точке 5 ламинарный слой турбулизируется в некоторой точке Т на границе зоны отрыва. С ростом числа Re^ линия перехода Т перемещается в направлении к линии отрыва S, так как при этом увеличивается турбулентность в кормовой вихревой области.
При достижении некоторого критического числа Рейнольдса Re дг 3-105-г-4-105 точка перехода совпадает с точкой отрыва. Следовательно, в точке отрыва слои —
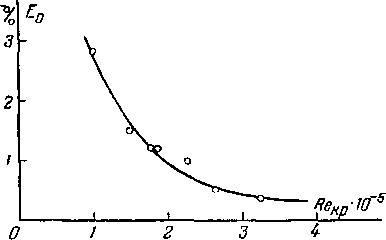
Рис. 5-44. Изменение критического числа Рейнольдса Re„„ в зависимости от степени турбулентности Е„ для М = 0.
турбулентный, обладающий большей сопротивляемостью отрыву. В результате изменения режима движения в слое вблизи отрыва точка S резко перемещается по потоку и обтекание шара улучшается кризисным образом: коэффициент сопротивления уменьшается в 2 — 4 раза (область V на рис. 5-43). Уменьшение с происходит за счет снижения сопротивления давления, так как сопротивление трения в турбулентном слое больше, чем в ламинарном. Это явление называют „кризисом сопротивления” плохо обтекаемых тел.
Положение линии перехода Т при Reoo<CReKp зависит
от степени турбулентности набегающего потока. Поэтому и критическое число ReKp существенно меняется в зависимости от'.?0. Соответствующая экспериментальная кривая приведена на рис. 5-44. При увеличении турбулентности до 3°/0 критическое число ReKp уменьшается почти в 3,5 раза.
Кривая на рис. 5-44 может быть использована для определения степени турбулентности набегающего потока по критическому числу ReKp. При этом критическим числом ReKp считают значение Re^, соответствующее коэффициенту сопротивления шара <^ = 0,3 (рис. 5-43).
Следует отметить, что при Re>ReKp (область VI на рис. 5-43) коэффициент сопротивления вначале несколько возрастает, а затем практически не зависит от Re: эта зона является второй областью автомодельности, соответствующей фиксированному положению точки отрыва турбулентного слоя.
Таким образом, на поверхности шара имеются три характерные точки: минимума давления (М), отрыва (S) и
перехода (Т), в которой происходит турбулизация слоя. Взаимное расположение точек М, S и Т оказывает решающее влияние на механизм обтекания и сопротивление шара при малых скоростях.
Изучение влияния сжимаемости на расположение указанных точек позволяет оценить изменение спектра обтекания' и сопротивления шара при переходе к большим числам М .
00*
Опыты показывают, что по мере увеличения числа Мм картина распределения давлений по обводу шара меняется (рис. 5-45). Важным является тот факт, что -при М > >Моо>0,3 с увеличением Мм давление в кормовой области за шаром снижается.
При Моо>М на поверхности шара образуются кольцевые зоны сверхзвуковых скоростей, которые замыкаются скачками уплотнения. Соответствующие спектры обтекания показаны на рис. 5-46. Влияние числа Re^ на этих режимах снижается, однако остается значительным. Только при Мда 3^0,8 влияния ReTC практически не наблюдается. В интервале Мм > М давление в кормовой области продолжает снижаться и достигает минимальных значений при 1,1 >0,8 (рис. 5-45).
Для больших дозвуковых скоростей характерны резкое сокращение диффузорной области и уменьшение градиентов давления в ней. При этих скоростях отрыв происходит в зоне расположения местных скачков уплотнения (рис. 5-46) независимо от того, каков режим течения в пограничном слое — ламинарный или турбулентный.
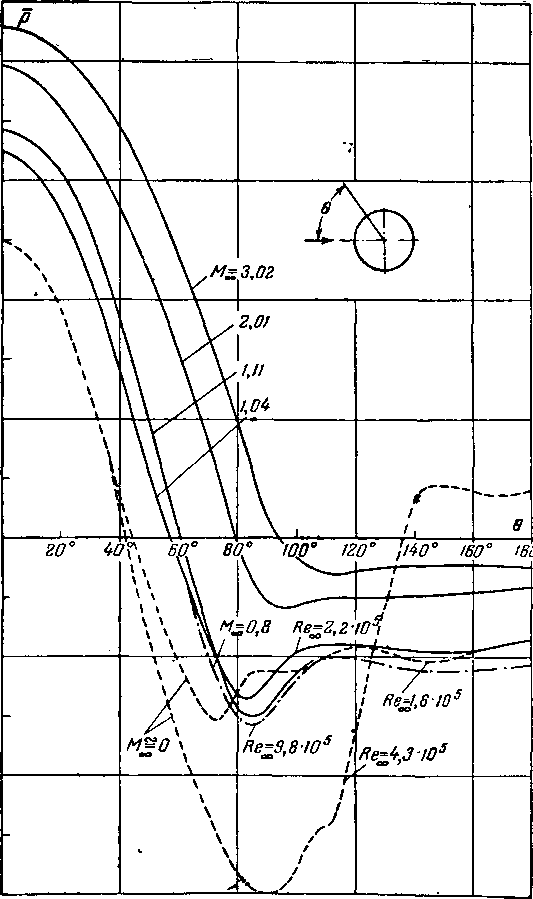

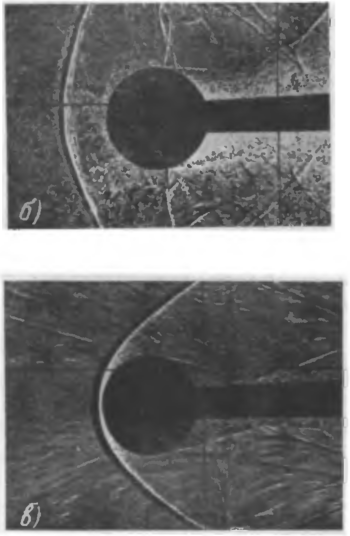
Рис. 5-46. Спектры обтекания шара при околозвуковых и сверхзвуковых скоростях, о —Мм -1.8; в-Моо = 3,0.
N
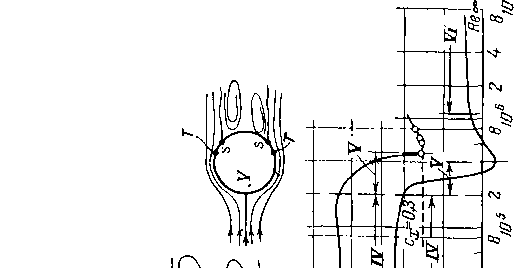
![]()
При больших сверхзвуковых скоростях (Мтс> 1,5) кривые давления имеют иной характер: давление в точках
минимума продолжает увеличиваться, диффузорный участок смещается по потоку. Давление в кормовой части шара с ростом сверхзвуковой скорости увеличивается.
Графики давлений можно использовать дл ориентировочного определения положения характерных линий на по-
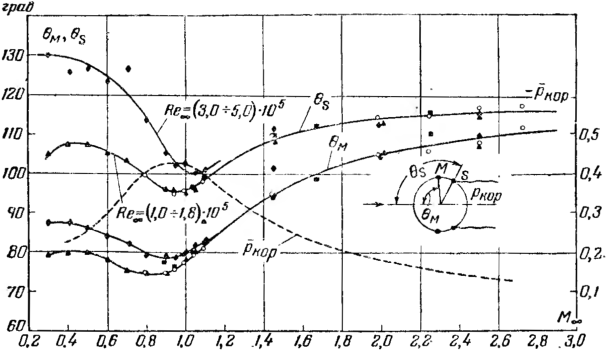
Рис. 5-47. Изменения положения линий минимума давления и отрыва в зависимости от числа Мж для шара. Изменение давления в кормовой части шара в зависимости от Ми (опыты автора).
верхности шара. Соответствующие кривые Ьм и 0S приведены на рис. 5-47'. Здесь можно видеть, что в диапазоне скоростей М = 0,3 ч-1,1 имеет место значительное перемещение линии отрыва, причем независимо от характера обтекания шара при Мсо = 0,2 значения 0^ и Ь5 уменьшаются, т. е. линия отрыва перемещается против потока и обтекание шара ухудшается.
Следовательно, как для Re^-CRe , так и для ReTO>
> ReKp влияние сжимаемости при Мю < 1 оказывается качественно одинаковым. С ростом Мтс обтекание шара приближается к тем условиям, которые отвечают отрыву ламинарного слоя. В области сверхзвуковых скоростей угол отрыва 0S возрастает с ростом числа и обтекание шара улучшается (рис. 5-47). Интенсивность смещения линии отрыва снижается при Мот>>2. В таких режимах перед шаром образуется криволинейный скачок уплотнения (рис. 5-46); в точках отрыва возникают слабые конические скачки.
Таким образом, в дозвуковой области с ростом числа Mffl линия отрыва перемещается к передней критической точке и при Мто=: 0,95-г-1,0 занимает наиболее близкое к ней положение, а при сверхзвуковых скоростях отрыв смещается в направлении к кормовой части. Отсюда можно заключить, что при дозвуковых скоростях с увеличением обтекаемость шара ухудшается, а при сверхзвуковых скоростях — улучшается.
Изложенное показывает, что при скоростях положение линий отрыва на шаре существенно зависит от режима течения в пограничном слое и, следовательно, от Re. Влияние сжимаемости здесь сказывается в том, что с увеличением Мм возрастает критическое число ReKp (рис. 5-47). Это означает, что турбулизация слоя в точке отрыва происходит при больших числах Re и линия перехода Т медленнее сближается с линией отрыва 5. Другими словами, сжимаемость затягивает переход ламинарного режима в турбулентный.
При 1 > Мм > М в исследованном диапазоне чисел Re^ кризисное изменение картины обтекания, связанное с турбулизацией слоя, вообще не обнаруживается и вне зависимости от Re^ обтекаемость шара резко ухудшается. Отсюда можно заключить, что при околозвуковых скоростях скачки приводят к отрыву ламинарного слоя примерно в одном и том же сечении.
Влияние числа на коэффициент сопротивления шара сх можно оценить по кривым на рис. 5-48. С увеличением М <М сх возрастает, причем при докризисном обтекании (Re^^ ReKp, кривая 1) коэффициенты сопротивления возрастают менее интенсивно, чем при закризисном (Re^^
> ReKp, кривая 2). При влияние ReM на сх
ослабевает и для М >0,8 кривые сх для различных Rew практически совпадают.
Полный коэффициент сопротивления шара можно представить в виде: ,
Сх Сх г + ^х кор>
сх кор — коэффициент кормового (донного) сопротивления.
На рис. 5-48 дополнительно представлены кривые сх кор “ сх (^оо)- Сопоставление кривых сх и сх кор показывает, что коэффициент головного сопротивление шара с =
1,1 1.0 0,9 0,8 0,7 О,В 0,5 0,4 0,3 0,2 0,1
|
сх | / ' Л— |
¦ | •X" ¦ |
|||||
| / Д | о Ч<\Г |
л и | 1 А ", | и | ||||
| / / |
/У. 7° | • о + А | j> испытания о труоах j Натурные испытания | |||||
|
— | \ \° / */ \ У 7v |
о | - По сро/. | I ; * ' & |
пера | |||
|
О С А |
i » / -1 а 7 / [У / |
-Схнор | ||||||
| сГ' • | i | ... 1 . | < - J _ |
д‘*“— | о *"Ъ*—. | " fa— | м* | |
О O.Z 0.4 0,6 0,8 1.0 t,Z 1,4 !,в 1,8 2,0 2,2 Z.4 2,6 2.8 3.0 3,2 3,4
Рис. 5-48. Коэффициенты сопротивления шара в зависимости от числа
аэродинами условиях.
по данным испытаний в аэродинамической трубе и в натурных
— сх — схк0 при дозвуковых скоростях возрастает незначительно. Следовательно, „волновой кризис* сопротивления шара в зоне околозвуковых скоростей, выражающийся в весьма резком увеличении сх (от 0,15 — 0,35 до 0,9 —
— 0,95), происходит главным образом за счет роста кормового сопротивления.
При сверхзвуковых скоростях сх продолжает расти и достигает максимального значения при М^-^1,6. Максимум кривой сх в этой зоне весьма пологий. При Мю >> 1 с х КОр интенсивно уменьшается.
На рис. 5-48 приведены также результаты других исследований. Характерно, что при околозвуковых и сверх-
звуковых скоростях все опытные данные хорошо совпадают1.
При Ми> 1 сопротивление плохо обтекаемого тела практически не зависит от Re.
5-15. ДВИЖЕНИЕ ГАЗА В КРИВОЛИНЕЙНЫХ КАНАЛАХ
При движении газа в криволинейных каналах возникают специфические явления. Действительно, рассмотрим течение газа по каналу постоянного сечения, в котором поток совершает поворот на 90° (рис. 5-49). Скорости движения в канале малы по сравнению со скоростью звука, так что влиянием сжимаемости можно пренебречь. В связи с тем, что частицы газа движутся по криволинейным траекториям, давление на внешней (вогнутой) и внутренней (выпуклой) стенках канала оказывается разным и различно меняется в направлении движения Так как частицы ядра потока под действием центробежных сил оттесняются к внешней стенке, то давление вдоль АВ возрастает по сравнению с давлением входящего потока р\, а вдоль АХВХ — уменьшается (рис. 5-49,а). За поворотом давление на вогнутой стенке снижается, а на выпуклой возрастает; на значительном расстоянии за поворотом давления выравниваются.
Таким образом, в сечениях криволинейного канала устанавливается неравномерное распределение скоростей и давлений; здесь возникает поперечный градиент давления. Частицы жидкости, движущиеся в пограничном слое вдоль плоских стенок, находятся под воздействием разности давлений и, обладая малой скоростью в направлении основного движения, перетекают к внутренней стенке, испытывая большее отклонение, чем частицы, более удаленные от стенок. По условию сплошности в ядре потока должны возникать компенсирующие течения, направленные к внешней стенке. В результате
1 На рис. 5-48 нанесена также кривая сх, построенная по формуле Эйлера:
^ = 0’5|1 + 2ML)'
Любопытно отметить, что формула Эйлера, полученная около 200 лет назад, дает близкие к опытным значения сх при Mm < 1.
в канале образуется вторичное вихревое движение, которое налагается на основной поток. Линии тока вторичного течения являются замкнутыми в поперечном сечении канала (рис. 5-49,6).
Вторичное течение состоит из двух потоков, которые около плоских стенок направлены к выпуклой поверх-
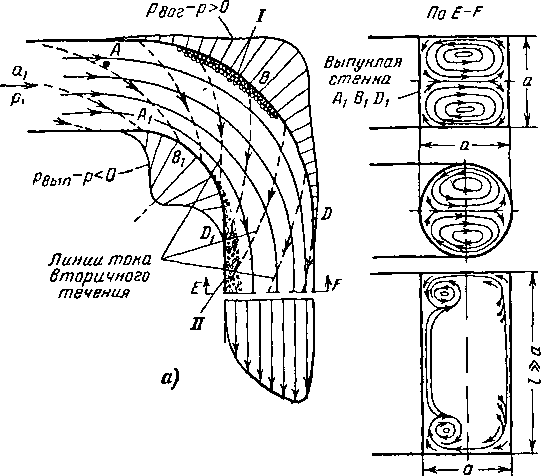
6)
Рис. 5-49. Схема потока в криволинейных каналах с различной формой поперечного сечения.
ности, а в центре канала — к вогнутой поверхности канала. Вторичные потоки имеют симметрично-винтовой характер. Линии тока вторичного течения на плоских стенках показаны пунктиром (рис. 5-49,а).
Вдоль участка вогнутой стенки АВ и вдоль участка выпуклой стенки B\DX течение диффузорно§. В зависимости от формы криволинейного канала здесь могут возникнуть отрывы (зоны / и II на рис. 5-49,а). Отрыв на 'вогнутой стенке АВ может быть локализован последующим «он'фузорным течением на участке BD. Отрыв на участке B\D\ имеет более значительную протяженность по потоку.
Структура вторичного течения в криволинейном канале и вызываемая им дополнительная потеря энергии существенно зависят от геометрической формы канала и режима потока (чисел Re и М).
Опыты показывают, что структура вторичных течений меняется при изменении формы сечения канала
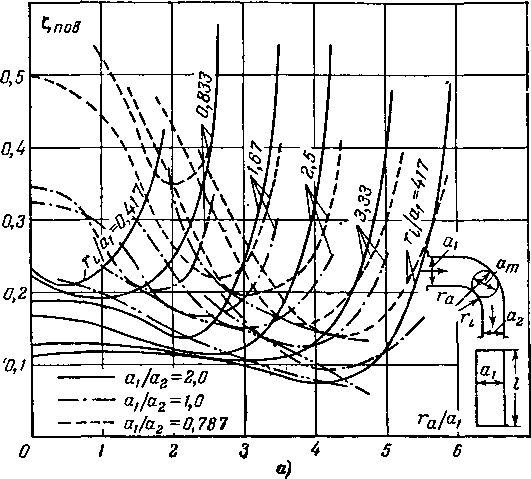
Рис. 5-50. Влияние радиусов кривизны вогнутой и выпуклой стенок ния проходных сечений канала с углом поворота
(рис. 5-49,6). Наибольшие отличия от рассмотренной выше схемы обнаруживаются в каналах с прямоугольной формой сечения (1>аи/<й). В случае вто
ричное движение газа по вогнутой и выпуклой стенкам затруднено,- так как частицы должны проделать длинный путь, на протяжении которого сказывается трение. Такое перетекание оказывается возможным только в пограничном слое вдоль плоских стенок; оно начинается на вогнутой поверхности (у плоских стенок)
и продолжается на .плоских стенках в направлении к выпуклой поверхности, где пограничный слой, участвующий в периферийном движении, сливается с пограничным слоем основного потока и интенсивно набухает. Вместе с тем благодаря движению в пограничном слое от вогнутой поверхности к выпуклой в ядре потока у плоских стенок образуются компенсирующие течения, направленные к вогнутой стенке Эти течения совместно
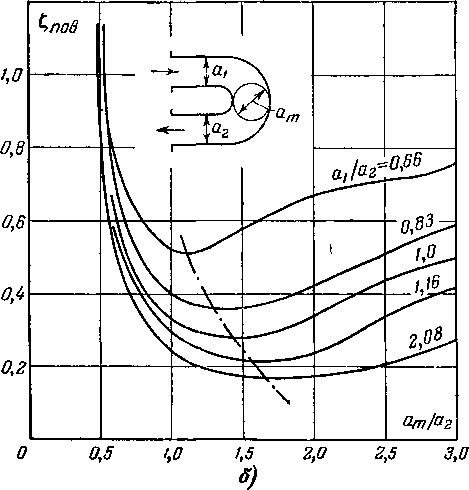
криволинейного канала с углом поворота 90° (а) и влияние соотноше-180° на потери по данным X. Нипперта (1/аг = 4).
с пограничным слоем, движущимся вдоль плоских стенок в противоположном направлении, образуют замкнутые вихревые области, охватывающие не все сечение потока, а только часть его в'близи выпуклой и плоских стенок. В рассматриваемом канале прямоугольного сечения вторичное течение .вырождается в пару вихрей, вращающихся в противоположных направлениях.
На образование вторичного течения затрачивается часть кинетической энергии потока. Потери энергии,
обусловленные кривизной канала, можно рассматривать как сумму: а) дополнительных потерь на трение аслед-ствие вторичного движения; б) вихревых потерь в зонах отрыва; в) потерь, вызванных вихревыми компенсирующими течениями. Наибольшую часть потерь составляют вихревые потери вследствие отрыва.
На рис. 5-50,а приведены данные X. Нипперта, характеризующие влияние некоторых геометрических характеристик канала на потери. Здесь коэффициент С определен как разность полных энергий на входе и выходе, отнесенная к скоростному напору на входе в канал.
Как видно из рис. 5-50,а Спов существенно зависит
от внутреннего гь и наружного га радиусов кривизны и
геометрической конфузорности канала, определяемой отношением а = —. Если <2 >1, то канал конфузорный,
й 2
а если а < 1, то канал диффузорный. При заданном отношении а изменение г или га приводит к изменению отно-
ат
шения ат=— и, следовательно, площади сечения вдоль
оси потока. Точки минимума кривых Спов соответствуют — га - г,
различным г =— в зависимости от г =—.Оптимальные
® Cly * Oj
значения rt несколько меньше га. При данном г. увеличение га'^>гаот приводит к особенно резкому возрастанию потерь. В этом случае криволинейный канал приобретает суживающе-расширяющуюся форму; скорости потока на повороте и потери возрастают.
Кривые на рис. 5-50,а отражают также влияние параметра а. В диффузорных каналах (а<1) потери выше, чем в каналах постоянного сечения (а= 1) и конфузорных
Во всем диапазоне значений г( и га огибающая крйвых
^пов (ri> га) лежит выше для диффузорного канала {а = = 0,787). Промежуточное положение занимает канал постоянного сечения (а=1).
Аналогичное влияние геометрического параметра а обнаруживается и для канала с углом поворота 180° (рис. 5-50,6). Минимум потерь в таких каналах отвечает
а ,
§ >* F и b o-¦>>
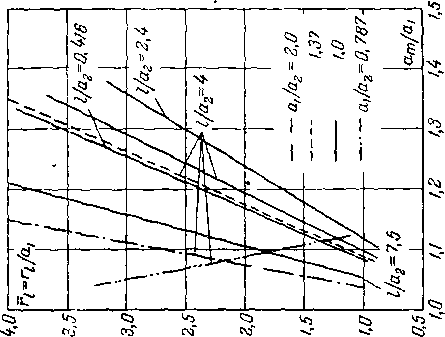
та
Зх'
w о
о Jt х*~
о и
i tsa >S «
о
аз
а
ч
о
Сц -Q
« 5
Ст* СО -
о о-о_ о
6н Н
«у t а
а ^
5 к
О-i
X <у
6 н ы о
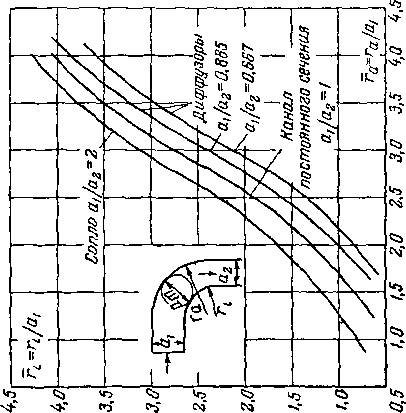
О С
а а
о а
и 33
к 2 §s <и о
9 и 5 d>
И з
S 2
о § о к
« S « 33 о Л о
ч ю со о
а „
н 0 Й о
о®
. «5 *-ч ь
"? о. ю о
. CQ
О о к CS
си
значениям ат > 1, причем оптимальное поджатие в выход ной части канала уменьшается с переходом к диффузор-ным каналам (а<[ 1).
На рис. 5-51 даны значения радиусов кривизны и соотношения характерных сечений канала, обеспечивающие минимальную интенсивность вторичных течений в криволинейном канале. Из графиков следует, что в диффузорных
и слабо конфузорных каналах целесообразно среднее сечение канала ат выполнять увеличенным (am> 1), а затем обеспечить конфузорное течение соответствующим поджатием
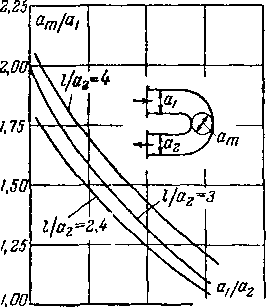
0,5 0,75 1,0
Рис. 5-52. Оптимальные значения ат в зависимости от геометрической конфузорности криволинейного канала аг по данным X. Нипперта. Угол поворота 180°.
> 1^. В этом случае умень-
шается разность давлении между вогнутой и выпуклой поверхностями в сечениях, где кривизна канала максимальна, и, следовательно, снижается —у интенсивность вторичных течений. Кроме того, поджатие выходной части канала сокращает область отрыва на выпуклой стенке А1В1 (рис.
5-49,а), а в некоторых случаях и предотвращает отрыв. Опыты X. Нипперта показали, что в зависимости от угла поворота, радиусов кривизны вогнутой и выпуклой стенок оптимальные соотношения величин ат и аг меняются.
Эти соотношения зависят также от геометрической конфузорности канала, т. е. от а. Опыты показывают, что с увеличением радиусов кривизны спинки и вогнутой поверхности потери от вторичных течений уменьшаются. Вместе с тем (рис. 5-51,а) с увеличением радиуса кривизны г. возрастает оптимальное значение ат при данных угле поворота потока и степени конфузорности (а). Зависимость ат от а, соответствующая минимальным потерям в криволинейном канале с углом поворота 180°, показана на рис. 5-52.
I -
соты канала — на оптимальное значение параметра а
О
Как видно из рис. 5-51,6, зависимость а
имеет
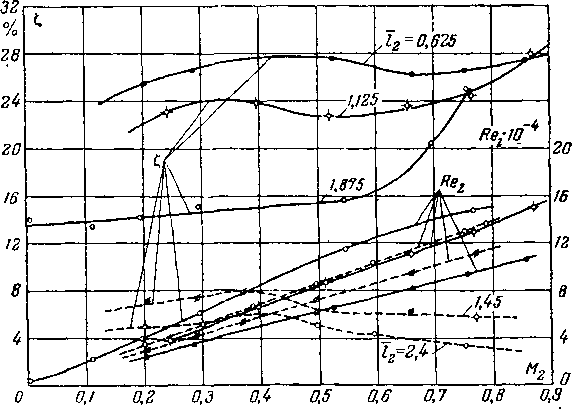
Рис. S-53. Изменение коэффициентов потерь в криволинейных каналах в зависимости от числа М2 на выходе (опыты В. И. Никитина).
максимум, положение которого определяется общей кон-фузорностью канала а.
Влияние двух важнейших режимных параметров — чисел Re и М — на потери и структуру потока в криволинейных каналах можно оценить по кривым на рис. 5-53. С увеличением Re потери в канале уменьшаются. Турбули-зация слоя вблизи отрыва приводит к смещению линии отрыва по потоку, что и вызывает резкое снижение потерь.
Влияние сжимаемости при докритических скоростях сказывается в том, что интенсивность вторичных течений снижается. Анализ кривых распределения давлений (рис. 5-54) показывает, что с ростом М уменьшаются поперечные градиенты давления в канале, так как коэффициенты давления возрастают более интенсивно на выпуклой поверхности, чем на вогнутой. При М>М. на вы-
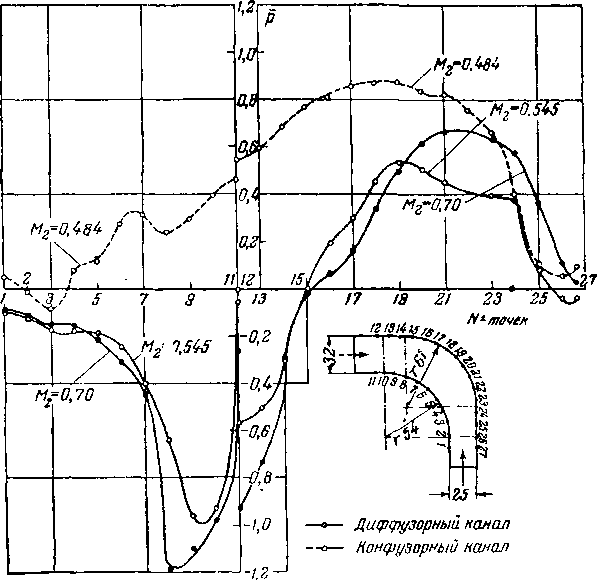
Рис. 5-54. Распределение давлений по контуру криволинейного^ канала. ----конфузорный канал, /2=2,4;--днф})узорный канал, /а=:1,875.
пуклой стенке возникают местные зоны сверхзвуковых скоростей и замыкающие их скачки. Отрыв потока, вызываемый скачками, приводит к росту коэффициентов потерь (рис. 5-53). При сверхзвуковых скоростях отмечается снижение потерь от вторичных течений.
5-16. ВРАЩАЮЩИЕСЯ ПОТОКИ ВЯЗКОГО ГАЗА
В § 5-1 отмечалось, что энтальпия торможения в потоке вязкого газа с неравномерным распределением скоростей является переменной величиной и условие t’o=const не может служить характеристикой течения и интегралом уравнения энергии адиабатического потока.
Наиболее отчетливо этот эффект обнаруживается вэ вращающихся потоках газа и, в частности, в вихревой трубе Ранка (рис. 5-55).
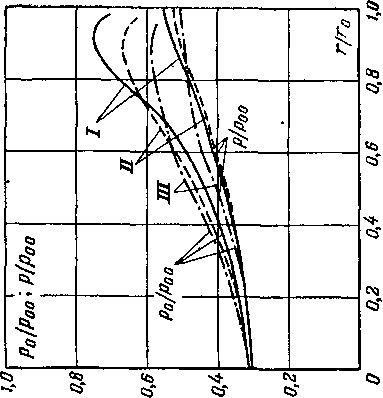
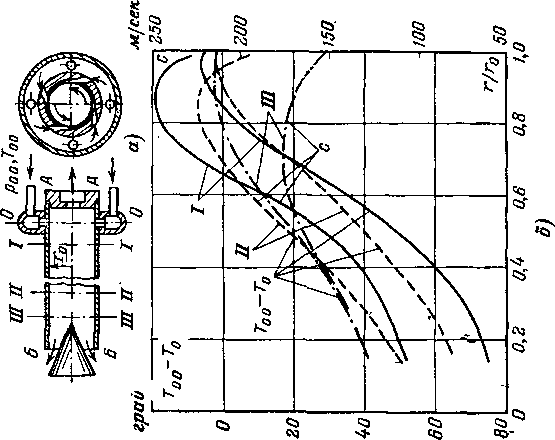
В вихревую трубу газ подводится соплами тангенциально пол давлением (сечение ОО на рис. 5-55,а!) и образует внутри трубы вращающийся поток. С одмой стороны (в сечении АА) поток выходит через отверстие, расположенное на оси трубы. На противоположном конце трубы выходное отверстие выполняется в виде кольцевой щели, расположенной у периферии (сечение ББ). Как показывает опыт, газ, вытекающий через центральное отверстие (в сечении АА), имеет значительно более низкую температуру торможения, чем на периферии в сечении ББ (рис. 5-55,6). Так; например, по данным И. Гартиетта и Б. Эккерта максимальная рааность температур торможения соответствует сечению /—/ и достигает величины Too—7’о=754-80° С. По мере удаления от сечения ОО профиль температур торможения выравнивается и в сечении III указанная разность достигает только 40° С. Характерно, что температура торможения на периферии Too меняется вдоль трубы менее интенсивно, чем температура на оси трубы, резко возрастающая к сечению ББ. Наиболее низкая температура торможения на оси соответствует сечению I—I. Следовательно, в такой трубе происходит температурное разделение газового потока, причем через центральное отверстие выходит сильно охлажденный газ.
Профили скоростей в различных сечениях показывают (рис. 5^55,6), что в трубе происходит интенсивная перестройка потока: скорости к периферии интенсивно снижаются к сечению III—III, а в ядре на оси иеоколько возрастают.
Неравномерное распределение скоростей по радиусу объясняет интенсивную диссипацир механической энергии, внутреннее тепловыделение и неравномерное распределение температуры торможения.
О весьма интенсивной диссипации энергии можно судить на основании опытных графиков распределения давления торможения и статического давления (рис. 5-55,в|).
Приближенное теоретическое решение рассматриваемой задачи можно получить для простейшего случая одномерного кругового движения газа. При этом полагаем, что поле осевых составляющих окорости в трубе равномерно. Поверхности тока такого вращательного движевия газа будут цилиндрическими: радиальные составляющие окорости и их производные обращаются в нуль. Пренебрегая влиянием массовых сил и считая движение установившимся, можно воспользоваться уравнением сохранения энергии (5-3) в цилиндрической системе координат:
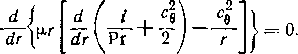
(5-79)
Здесь Сд — окружная (тангенциальная) составляющая скорости. Принимая, кроме того, ^ = const и Рг = const, уравнение (5-79), можно проинтегрировать. Общий интеграл (5-79) для рассматриваемого случая получен JI. А Вулисом в таком виде:
![]()
Для получения искомой связи в конечном виде необходимо знать закон изменения с0 (г). Целесообразно рассмотреть два предельных случая: а) в предположении циркуляционного (квазипотенциального) течения, распределение скоростей в котором подчиняется условию СдГ = const, (§ 1-2), и б) для линейного распределения скоростей Cg/r = const, соответствующего вихревому ядру (квазитвердое течение) (§ 1-2).
В первом случае после подстановки в (5-80)
2 2
ся гп 2_ 00 О
св~- гг >
где св — тангенциальная составляющая скорости в периферийном
0 сечении, вне пограничного слоя; г0 — радиус трубы, можно получить:
с2 с2
«„ = « + -Y = (1 - 2Pr) ~ + const, (5-81)
2 г*
— Г
где г=——относительный радиус;
/0 — текущее значение энтальпии торможения.
Постоянную в правой части находим, записывая (5-81) для сечения г = г0, г=1. Тогда
ho (1 — 2Pr) g •
Здесь i00 — энтальпия торможения в сечении г = 1 (в периферийном сечении трубы).
После подстановки значения постоянной в (5-81) окончательно находим
Так как смакс = V2/00 — максимальная скорость в периферий-
макс
ном сечении, то
с2о _ 4:034
2<«. А ~ ?°C0S
00 емакс
где а0 — угол между вектором скорости с0 и плоскостью вращения газа.
Следовательно,
? = 1 _ (1 _ 2Pr) (l- -==-) Egros*«... (5-82а)
Из уравнения (5-82а) следует, что при условии c0r = const энтальпия торможения возрастает с приближением к стенкам трубы,
если число Рг > 0,5. При Рг = 0,5 энтальпия торможения сохраняетси постоянной по радиусу, а при Рг 0,5 — возрастает к оси трубы.
св
Для закрутки потока по закону — — const из (5-80) нетрудно получить следующую формулу:
с2
А = 1 _ (1 — fi) = 1 — (1 —72) со$Ч. (5-83)
iQQ ^100
В этом случае вне зависимости от значения числа Прандтля энтальпия торможения уменьшается к оси трубы.
Очевидно, что если для двух различных законов распределения скоростей по радиусу энтальпия торможения уменьшается к оси трубы, то и для любого промежуточного закона будет иметь место аналогичное изменение (080.
Представляет интерес оценить изменение энтальпии торможения
-
по радиусу в долях кинетической энергии 1 Обозначим:
где i10 — энтальпия движущегося газа в сечении г = г0.
Использовав формулы (5-82а) и (5-83), получим для двух различных законов распределения скоростей:
Д(0 = (1 — 2Pr) ^1— cos2 а0;
Дг'о = (1 — г2) cos2 а0.
Л. А. Вулисом рассмотрен более общий случай распределения скоростей, отвечающий уравнению
При этом интеграл (5 80) после обычных преобразований принимает вид:
cos2 а0. (5-84)
Отсюда следует, что при таком круговом движении при Рг 0 энтальпия торможения меняется вдоль радиуса.
Для плоскопараллельного течения с неравномерным распределением скоростей энтальпия торможения определяется формулой (5-2).
Распределение статической температуры йо сечению вращающегося потока газа устанавливается с помощью уравнения энергии (5-80). Рассматривая частные случаи закрутки по законам c^r = const
с0
и — = const и вспоминая, что
О
• - • л. —
h — » + о .
из формул (5-82а) и (5-83) находим:
4-^ = 1.
*ОП Ton
+ 2^=--lj Prj 6* cos* а, (5-85)
для = const н
7—= 1 — (1 — г2)2 Й cos2 я0 (5-86)
ton 1 on
для — = const.
Изменение статического давления по радиусу можно найти, пользуясь уравнениями движения в цилиндрических координатах. С учетом основных допущений (радиальные составляющие скорости и продольные градиенты давления малы, поле осевых скоростей равномерно) первое уравнение системы (1-17) приобретает следующий вид:
1 dp се
— ~=—. (5-87
р dr г у
Смысл уравнения (5-87) состоит в том, что оно выражает условие радиального равновесия частицы газа, совершающей вращательное движение.
Учитывая, что
gRT (ft-1 )Г
представим (5-87) в новой форме:
dp k с\ dr
(5-88)
Подставив сюда i из формул (5-85) и (5-86), после интегрирования можно получить приближенные зависимости р(г).
Полученные выше формулы изменения параметров по сечению вихревой трубы могут быть использованы, если известна скорость на периферии трубы . Для расчета потока в различных сечениях по длине трубы необходимо располагать опытными зависимостями с0о (х) и а0(х) (х— расстояние по оси трубы).
В соответствии с изменением с0<1 по длине трубы меняется и распределение всех параметров по радиусу81. В некоторых сечениях происходит выравниваний поля статических давлений и температур и температур торможения, причем эти сечения (р = const; Т = const и Т„ = const) ие являются совпадающими.
М. Г. Дубинским теоретически доказано, что в сечении с постоянной статической температурой по радиусу достигается максимум энтропии вращающегося потока газа. Следовательно, закрученный поток в вихревой трубе стремится к равновесному состоянию, которое и достигается в сечении с Т = const.
Выравнивание потока в вихревой трубе иллюстрируется графиками на рис. 5-55.
Таким образам, в вихревой трубе обнаруживается эффект температурного .разделения газа, который может быть использован для целей охлаждения различных тел и, в частности, в холодильных усташовках кратковременного действия и пр. Вместе с тем этот эффект заслуживает дальнейшего подробного теоретического и экспериментального изучения, так как о.н проявляется во всех случаях, когда возникает вращательное движение газа (ступень турбо-машины, в'ихревой насос и др.).
Необходимо подчеркнуть, что неравномерное распределение температур торможения в адиабатическом потоке вязкого газа, связанное с неравномерным распределением скоростей, обнаруживается и при внешнем обтекании тел (в пограничном слое и в .кормовом следе). Во всех случаях, когда выделяющаяся теплота трения82 не равна количеству тепла, отводимому теплопроводностью, имеет место неравномерное распределение полной энергии.
Значительный интерес представляет движение закрученного потока в цилиндрической кольцевой трубе83. В этом случае исходное уравнение энергии (5-79) необходимо проинтегрировать для кольцевого вращающегося потока.
