Моделирование разработки нефтяных месторождений
МОДЕЛИРОВАНИЕ РАЗРАБОТКИ ;НЕФТЯНЫХ МЕСТОРОЖДЕНИЙ
§ 5. МОДЕЛИ ПЛАСТОВ И ПРОЦЕССОВ РАЗРАБОТКИ
Под моделью в широком научном смысле этого слова понимают реально или мысленно созданную структуру, воспроизводящую или отражающую изучаемый объект. Название модель происходит от латинского слова modulus, что означает “мера, образец”. Моделирование принадлежит к числу основных методов познания природы и общества. Оно широко используется в технике и является важным этапом в осуществлении научно-технического прогресса.
Создание моделей нефтяных месторождений и осуществление на их основе расчетов разработки месторождений - одна из главных областей деятельности инженеров и исследователей-нефтяников.
На основе геолого-физических сведений о свойствах нефтяного, газового или газоконденсатного месторождения, рассмотрения возможностей систем и технологий его разработки создают количественные представления о разработке месторождения в целом. Система взаимосвязанных количественных представлений о разработке месторождения - модель его разработки, которая состоит из модели пласта и модели процесса разработки месторождения.
М о д е л ь п л а с т а - это система количественных представлений о его геолого-физических свойствах, используемая в расчетах разработки месторождения. М од е л ь п р о ц е с с а р аз -р а б о т к и месторождения - система количественных представлений о процессе извлечения нефти и газа из недр. Вообще говоря, в модели разработки нефтяного месторождения можно использовать любую комбинацию моделей пласта и процесса разработки, лишь бы эта комбинация наиболее точно отражала свойства пластов и процессов. Вместе с тем выбор той или иной модели пласта может повлечь за собой учет в модели процесса каких-либо дополнительных его особенностей и наоборот.
Модель пласта следует, конечно, отличать от его расчетной схемы, которая учитывает только геометрическую форму пласта. Например, моделью пласта может быть слоисто-неоднородный пласт. В расчетной же схеме пласт при одной и той же его модели может быть представлен как пласт круговой формы, прямолинейный пласт и т.д.
Модели пластов и процессов извлечения из них нефти и газа всегда облечены в математическую форму, т.е. характеризуются определенными математическими соотношениями.
Главная задача инженера, занимающегося расчетом разработки нефтяного месторождения, заключается в составлении расчетной модели на основе отдельных представлений, полученных в результате геолого-геофизического изучения месторождения, а также гидродинамических исследований скважин.
Современные компьютерно-вычислительные достижения позволяют со значительной детальностью учитывать свойства пластов и происходящих в них процессов при расчетах разработки месторождений.
Непрерывно расширяются возможности геолого-геофизиче-ского и гидродинамического познания объектов разработки. И все же эти возможности далеко не безграничны. Поэтому всегда возникает необходимость построения и использования такой модели разработки месторождения, в которой степень познания объекта и расчетные требования были бы адекватными.
Нефтяные месторождения как объекты природы обладают весьма разнообразными свойствами. Известно, что нефть может насыщать не только пористые песчаники, но и находиться в микроскопических трещинах, кавернах, имеющихся в известняках, доломитах и даже в изверженных породах.
Одна из основных особенностей нефтегазосодержащих пород - различие коллекторских свойств (пористости, проницаемости) на отдельных участках пластов. Эту пространственную изменчивость свойств пород-коллекторов нефти и газа называют л и т о л о г и ч е с ко й н е о дн о р од н о с т ь ю пластов.
Вторая основная особенность нефтегазоносных коллекторов - наличие в них трещин, т.е. т р е щи н о в а т о с т ь пластов.
При разработке месторождений эти особенности нефтегазоносных пород оказывают наиболее существенное влияние на процессы извлечения из них нефти и газа.
Модели пластов с известной степенью условности подразделяют на детерминированные и вероятностно-статистические.
Детерминированные модели у нефтяников получили название “адресные модели”.
Детерминированные, или адресные, модели - это такие модели, в которых стремятся воспроизвести как можно точнее фактическое строение и свойства пластов. Каждая деталь адресной модели точно должна соответствовать детали стр оения реального пласта. Адресная модель при все более детальном учете особенностей пласта должна стать похожей на “фотографию” пласта. Например, на рис. 25 показан в плане реальный пласт с отдельными участками пористостью mj и проницаемостью kj. В действительности строение пласта, показанного на этом рисунке, более сложное. Однако с определенной степенью точности схему этого пласта можно считать его расчетной моделью. Практическое применение адресных моделей пластов стало возможным благодаря широкому развитию быстродействующей вычислительной техники и соответствующих математических методов. При расчете данных процессов разработки нефтяного месторождения с использованием адресной модели всю площадь пласта или его объем разбивают на определенное число ячеек в зависимости от заданной точности расчета, сложности процесса разработки и мощности компьютера. Каждой ячейке придают те свойства, которые присущи пласту в области, соответствующей ее положению.
Дифференциальные уравнения разработки месторождения заменяют конечно-разностными соотношениями, а затем производят компьютерный расчет.
Вероятностно-статистические модели не отражают детальные особенности строения и свойства пластов. При их использовании ставят в соответствие реальному пласту некоторый гипоте-
12 3
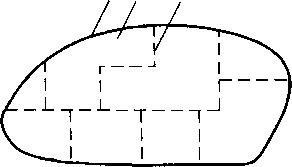
Рис. 25. Схема детерминированной модели пласта с участием различной пористости и проницаемости:
1 - условный контур нефтеносности; 2 - участок пласта с пористостью пород mj и проницаемостью kj; 3 - границы участков пласта с различными пористостью и п р оницае-мостью
тический пласт, имеющий такие же вероятностно-статистические характеристики, что и реальный. К числу наиболее известных в теории разработки нефтяных месторождений вероятностно-статистических моделей пластов относятся следующие.
1. Модель однородного пласта. В этой модели основные параметры реального пласта (пористость, абсолютная и относительная проницаемости), изменяющиеся от точки к точке, ос-редняют. Часто, используя модель такого пласта, принимают гипотезу и о его изотропности, т.е. равенстве проницаемостей в любом направлении, исходящем из рассматриваемой точки пласта. Однако иногда считают пласт анизотропным. При этом принимают, что проницаемость пласта по вертикали (главным образом вследствие напластования) отличается от его проницаемости по горизонтали. Модель однородного в вероятностностатистическом смысле пласта используют для пластов с действительной небольшой неоднородностью.
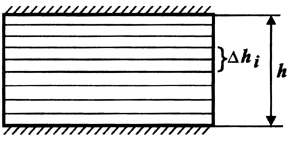
2. Модель слоистого пласта. Эта модель представляет собой структуру (пласт), состоящую из набора слоев с пористостью mj и проницаемостью kj (рис. 26). При этом считают, что из всей толщины пласта h слои с пористостью в пределах Amj и проницаемостью в пределах Akj составляют часть A hj. Если каким-либо образом, например, путем анализа кернового материала, геофизическими методами и т.д., измерять проницаемость отдельных прослоев пласта в различных скважинах, то окажется, что из суммарной толщины всех измеренных пропластков h часть их Ah1 обладает проницаемостью в пределах Ak1. Другая часть пропластков Ah2 будет иметь проницаемость в пределах Ak2 и т.д. Можно для реального пласта построить зависимость
A h/ h = f(kj)A kj (II.1)
и на ее основе создать модель слоистого пласта, которая будет представлять собой структуру, состоящую из набора прослоев различной проницаемости и характеризующуюся той же функцией (II. 1), что и реальный пласт.
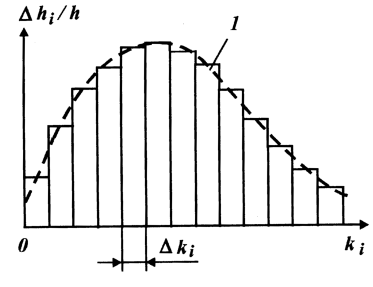
С помощью зависимости вида (II. 1) построена гистограмма (рис. 27), где ступеньками представлены доли общей толщины пласта, которые занимают пропластки с соответствующей проницаемостью.
Рис. 27. Гистограмма проницаемости:
1 - кривая, аппроксимирующая гистограмму
3. Модель трещиноватого пласта. Если нефть в пласте залегает в трещинах, разделяющих непористые и непроницаемые блоки породы, то модель такого пласта может быть представлена в виде набора непроницаемых кубов, грани которых равны I*, разделенных щелями шириной Ь*. Реальный пласт при этом может иметь блоки породы различной величины и формы, а также трещины различной ширины. Сечение реального пласта площадью A S показано на рис. 28, где i-я трещина имеет длину I, и ширину Ь,. На рис. 29 показано сечение модели этого пласта A S площадью, представляющей собой набор квадратов со стороной I* и шириной трещин Ь*. Рассмотрим наиболее существенные осредненные, а потому и вероятностно-статистические характеристики трещиноватого
пласта.
Известно, что скорость v4 течения вязкой жидкости в единичной трещине в направлении, перпендикулярном к плоскости (см. рис. 28), определяется следующей зависимостью:
АР
(II.2)
v
12ц AxАх—
ь2 ар
12ц дх
Расход жидкости A q, протекающей через сечение площади AS в направлении х, выражается следующим образом:
2 b3|i dp
- AS dp
(II.3)
AS 12ц dx
Введем понятие пустоты трещин Ёт, определяемой формулой
2i
AS
Е т
2AS
AS — 0
(II.4)
а также средней ширины трещин Ь*. Тогда из (II.3), (II.4) получим выражение для скорости фильтрации в трещиноватом пласте
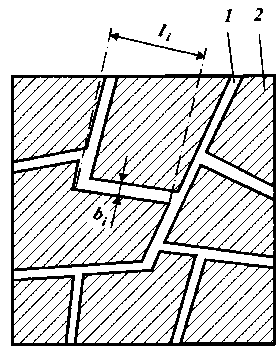
Рис. 28. Сечение трещиноватого пласта:
1 - трещины; 2 - блоки породы
I*
| 1 | 1 | ж | ж | |
|
"Ж | 1 |
ш | Ш |
ж |
| t |
if | 9 | ж | ж |
| +- | у//// |
///// |
у/// | |
|
у/// | ш |
/ЛУ/ |
Рис. 29. Сечение модели трещиноватого пласта площадью AS:
1 - блоки породы; 2 - трещины
ASas — 0 12ц AS dXAS— 0 6ц дх
Выражение (II.5) - аналог формулы закона Дарси для трещиноватых пластов. При этом проницаемость трещиноватого пласта
кт - Ь*3Ет/6. (II.6)
Можно получить выражение для трещинной пористости тт, принимая ее равной “просветности” сечения трещиноватого пласта. Имеем
2ь^ ь*21
as--2Ь* ЕТ.
asas—о asas—о
ь3 Е1'
Ь* AS
(II.5)
П р и м е р . II. 1. В результате гидродинамических и геофизических исследований трещиноватого пласта известно, что кт = 1 мкм2, тт = 0,2 • 10-2. Требуется определить среднюю ширину трещин b* и их густоту Ёт.
Из формул (II.6) и (II.7)
ь (12кт +1/2
ь*- * "тт- •
Тогда
- 7,74 • 10 м = 77, 4 мкм;
Ь* Ет Эр
Aq
др
Vt
тт - -AS
(II.7)
^ тт 0,2 • 10-12 13
Ьт - —— - 13 трещина/м.
2Ь. 2 • 7,74 • 10-5
Таким образом, в данном случае “модельная” густота трещин равна 13 трещинам на 1 м ствола скважины.
4. Модель трещиновато-пористого пласта. В реальном пласте, которому соответствует эта модель, содержатся промышленные запасы нефти как в трещинах, так и в блоках, пористых и проницаемых. Эта модель также может быть представлена в виде набора кубов с длиной грани I., разделенных трещинами со средней шириной Ь.. Фильтрация жидкостей и газов, насыщающих трещиновато-пористый пласт, происходит как по трещинам, так и по блокам. При этом вследствие значительной проницаемости трещин по сравнению с проницаемостью блоков любые изменения давления распространяются по трещинам быстрее, чем по блокам, в результате чего для разработки трещиновато-пористых пластов характерны перетоки жидкостей и газов из блоков в трещины и наоборот.
Все перечисленные модели (однородного, слоистого, трещиноватого, трещиновато-пористого пластов) отнесены к вероятностно-статистическому классу. Если же реальный пласт действительно весьма однородный, соответствующую модель однородного пласта можно считать детерминированной. Однако в природе совершенно однородные пласты встречаются крайне редко.
§ 7. ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКОЕ ОПИСАНИЕ СВОЙСТВ ПЛАСТОВ
Теория вероятности и математическая статистика используются не только для построения моделей пласта, но и, прежде всего, для количественного описания свойств реальных пластов. При вероятностно-статистическом описании пластов наиболее важны следующие понятия теории вероятности.
1. Плотность статистического распределения параметров пласта или просто плотность распределения. Применительно к описанию слоистого пласта она отражает вероятность появления слоя (пласта или пропластка), имеющего значение некоторого параметра (например, абсолютной проницаемости), изменяющегося в пределах от x до x + A x (A x - малая величина) В модели слоистого пласта плотность распределения в пределе
А^ — 0 есть аналитическое выражение гистограммы, определяемой формулой (II. 1). В случае же однородного по площади пласта гистограмма проницаемости по аналогии с (II. 1) имеет вид
^ - f (ki)Aki, (II.8)
где ASi - часть общей площади нефтеносности S проницаемостью ки Плотность распределения некоторого параметра пласта I обозначим через f( I ).
2. Функция или закон распределения параметра пласта I, определяемая формулой
F(x) - Jf (x)dx + c (II.9)
Так что f(x) = F'(x).
3. Математическое ожидание а ( I) непрерывной случайной величины х, причем
М(х) - Jxf (x)dx. (II. 10)
Используют также понятие дисперсии случайной величины и другие понятия теории вероятности.
Для вероятностно-статистического описания распределения абсолютной проницаемости к в моделях слоистого и неоднородного по площади пластов в основном применяют следующие законы.
1. Н ор ма л ь н ы й з ак он р ас п р е д е л е н и я (закон Гаусса). Для этого закона плотность распределения проницаемости выражается следующей зависимостью:
(k-k)2
f (k) -—^ в 2a2 , (II.11)
a\ 2n
где параметр a будет определен ниже.
По нормальному закону распределения пределы изменения к следующие: - » < к < ». Абсолютная проницаемость пласта к, которую будем называть просто проницаемостью, конечно, не может принимать отрицательных значений, как и не может быть бесконечно большой. Однако по нормальному закону распределения проницаемость может быть отрицательной и бесконечной. Для избежания этого несоответствия можно исключить из нормального закона ту часть, которая соответствует изменению проницаемости в пределах - » < к < 0. Для полного нормального закона распределения проницаемости F^) имеем следующее выражение:
(k-k)2
(II.12)
-га ay 2 л
Рассмотрим процесс вычисления интеграла (II. 12). Для этого разобьем (II. 12) на части следующим образом:
(k-k)2
(k-k)2
(II. 13)
Полагая далее к - k = - j, из (II. 13) получаем
2
0 1 - т “ 1
¦e 2a2 dj.
F1(k) - 72^e 2a dj - 0
(II.14)
» ay 2n 0 ay 2n
Обозначим
j = aV2
тогда
X; - dX,
ay 2
2
j
f—в 2a2 dj - f-Le-X2 dX - -;
(II.15)
0 ay 2n 0 у n 2
(k- k)2
F2(k) - J——e 2a2 dk - — erfi
(k-k)2
2 aV2
(II.16)
erf
л/2 , aV 2n Окончательно имеем
( k - k +
2
т
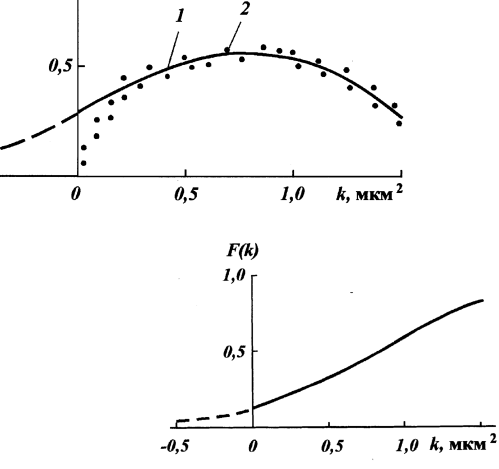
_i_
н0,5
Рис. 30. График плотности нормального распределения про
ницаемости при а = 0,7, к = = 0,8 мкм2:
1 - теоретическая кривая; 2 -фактические точки
Рис. 31. Кривая, построенная по формуле нормального закона распределения проницаемости при а = 0,7, к = 0,8 мкм2
На рис. 30 показан график плотности распределения f(k), определенной по формуле (II.11), а на рис. 31 изображена кривая, построенная по формуле закона распределения в соответствии с формулой (II. 17). Даже если в данном случае фактическое распределение проницаемости достаточно хорошо описывается формулой нормального закона распределения при больших значениях проницаемости k, в области незначительных значений к теоретическое и фактическое распределения проницаемости явно расходятся вследствие влияния отрицательных проницаемостей, которые допускает нормальный закон р аспр е-деления.
Поскольку erf(ro) = 1, то, согласно (II. 17), F(^) = 1. В соответствии с (II. 10) математическое ожидание проницаемости
есть средняя проницаемость к . Покажем это, для чего подставим (Ii.11) в (II.10). Получим
(k-k)2
ю--
M(k) = f-k~e 2°2 dk. (II.18)
—<х> а \ 2п
Для вычисления интеграла (II. 18) представим его следующим образом:
-(k_k>2 k Ie 2a2dk = l4 + l2.
( k — k
M(k) = f
(II.19)
—ю) ay 2n ay 2n ,
Для первого интеграла 11 имеем следующее выражение:
- (k_k>_
I = f e 2°2dk.
—™ay 2п
(II.20)
Положим X = (к - k )/a V2). Тогда из (II.20) получим
| = ф fxe-x2 dX = aji | — e-X = 0.
уп —ю 2л/ п —ю
(II.21)
Второй интеграл 12 выразим следующим образом:
(k— k)2
_ Ю---
12 = k f—=e 2a2 dk = k
(k—k)2
(k—k)2
f-L=e 2a2dk + f—^=e 2a2 dk
ay 2n
(II.22)
f f2~' —ю ay 2n
л/2^
0 a-
По аналогии с (II. 14) и (II. 15) каждый из интегралов, входящих в (II.22), равен 1/2. Поэтому с учетом того, что, согласно (II.21), 11 = 0, а 12 = k , выражение (II.19) превращается в тождество. Наконец, определим, чему равна дисперсия при нормальном законе распределения. Получим
_ (k—k)2
ю — 2 —ю (ъ |,л2--—
D(k) = f
(k — k) f (k)dk = k f(k ~pl e
2a2 dk
(II.23)
-e
—Ю a^j 2n
Для вычисления (II.23) введем, как и ранее, величину X = (к -
- К k )/( aV2 ). Тогда из (II.23) имеем
D(k) = ^ fX2eXdX = ^_jfX2e-x2dX + fX2ex2dX| = fX2eXdX.
уп —ю уп [—ю о , Vn 0
(II.24)
Входящий в (II. 24) определенный интеграл табличный. Он, как известно, выражается следующим образом:
fX2e-X dX = ^. (II.25)
о 4
Из (II.24) и(11.25) получим D(k) = a2. (II.26)
2. Л о г а р и ф м и ч е с к и н о р м а л ь н ы й з а к о н . Формула
плотности распределения проницаемости при этом законе име
ет следующий вид:
(lnk— lnk) 2?
1
f (k) =
(II.27)
0 < k < ю.
у kV2n
Плотность логарифмически нормального распределения показана на рис. 32. Найдем F(k). Подставляя (II.27) в (II.9), получим
(lnk — lnk)
k1 F<k)=/д
(II.28)
dk.
,V2n
Поскольку d(lnk) = dk/k, из (II.28) имеем
(lnk — lnk)
ln k 1 —
F« = f-T- e
ay 2n
2a
d(ln k).
(II.29)
Отсюда аналогично (II. 17) получим
l lnk — lnk +
V aV2
(II.30)
1 + erf
Математическое ожидание проницаемости п р и
логарифмически нормальном законе распределения получим по формуле
(II. 10). При этом
(II.31)
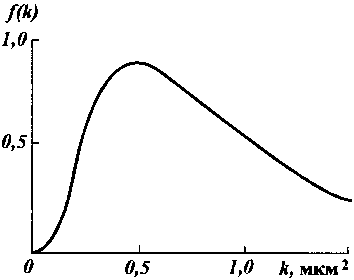
M (k) = k e
a 2/2
Рис. 32. График плотности логарифмически нормального рас
пределения при a = 0,7, k = = 0,8 мкм2
3. Г а м м а - р а с п р е д е л е н и е. Плотность гамма-распределения абсолютной проницаемости в общем виде выражается следующим образом:
k a
(II.32)
f (k) =
0 < k <ю.
Ё(a)kа При этом
00
Ё = (a) = fe xxa *dx, a >0, x > 0.
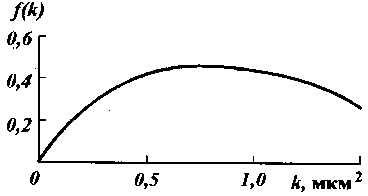
Плотность гамма-распределения представлена на рис. 33. Формула закона распределения проницаемости имеет вид
kka-1e-k/k
dk
(II.33)
0 Ha) k a Как и во всех случаях,
<х> - x a-1
. a-1 -k/k ..
k e dk
ЁМК a
dx
=f1
(II.34)
F(») = f
1, x = k/k.
Ё^)
0
0
Математическое ожидание проницаемости при гамма-распределении определяется следующим образом:
Ё(a + 1)
ЁМ
kdx
(II.35)
M (k) = /?-
k = ak.
Ё(a)
4. 3 а к о н р а с п р е д е л е н и я М а к с в е л л а . При расчетах показателей процесса разработки нефтяных месторождений используют также формулу закона распределения Максвелла, полученную им для описания распределения молекул газа по скорости. Форма записи формулы этого закона была изменена М. М. Саттаровым и Б. Т. Баишевым с целью описания распределения проницаемости. Видоизмененная М. М. Саттаровым формула плотности распределения выражается следующим образом:
k+ a
-a < k < ro,
f (k) = П=Л
vn i
k0 k0
(II.36)
Рис. 33. График плотности
гамма-распределения a = 2, k =
= 0,8 мкм2
Рис. 34. График плотности распределения по Максвеллу, видоизмененный М.М. Саттаровым при
к0 = 0,8 мкм2, $ = 0,1 мкм2
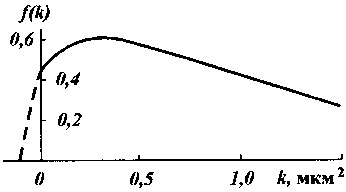
где а, к0 - параметры распределения, определяемые на основе обработки данных о геолого-физических свойствах пластов. Формула плотности распределения проницаемости, по Б. Т. Ба-ишеву, имеет вид
(k+а)2
2--
f((k) =
-1(k +
а) — е
k2 , (II.37)
Vn k2 k1
1
где a, k2 - параметры распределения.
На рис. 34 показан график f(k), построенный по формуле (II.36). Как видно, закон допускает существование нереальных значений отрицательной проницаемости. Однако, как и в случае нормального закона, можно считать, что проницаемость изменяется в пределах 0 < к < <*>, но следует учитывать, что в пласте есть некоторая отличная от нуля доля слоев с нулевой проницаемостью.
§ 8. ОСНОВЫ МЕТОДИК ПОСТРОЕНИЯ МОДЕЛЕЙ ПЛАСТОВ ПО ГЕОЛОГО-ФИЗИЧЕСКИМ И ПРОМЫСЛОВЫМ ДАННЫМ
Создание модели пласта на основе часто разрозненных геолого-физических и промысловых сведений о нем требует от инженера-разработчика глубоких знаний, проявления научного, творческого подхода. Нефтегазоносные пласты не похожи друг на друга. При их моделировании инженер-разработчик обычно использует только общий опыт построения моделей пластов в примерно аналогичных случаях, но у него нет и не может быть такой методики, слепо следуя которой, он мог бы создавать модель пласта в каждом конкретном случае. Построение модели пласта всегда связано с научным поиском.
Для создания модели пласта используют сведения о его геологическом строении; результаты исследований образцов пород, отобранных при бурении из продуктивного пласта; данные промыслово-геофизических работ и бурения скважин; индикаторные кривые и кривые восстановления давления в скважинах; данные разработки пласта в начальной стадии.
ПОСТРОЕНИЕ АДРЕСНОЙ МОДЕЛИ ПЛАСТА
При построении этой модели, которая может быть практически использована для расчетов разработки пластов лишь с помощью современных компьютеров, привлекают данные, полученные в результате геологического, геофизического и гидродинамического изучения месторождения, а также предшествующего периода его разработки, если такой имеется.
При этом применяют следующую примерную последовательность действий.
1. Проводят анализ данных сейсмического изучения месторождения, в результате чего определяют форму залегания характерных объектов пласта (кровли, подошвы, непроницаемых пропластков и т.п.), газонефтяного и водонефтяного контактов, геологических нарушений (разломов, зон выклинивания пластов и т.д.).
2. Осуществляют интерпретацию геофизических и гидродинамических исследований пластов в скважинах, например,
стандартных измерений кажущегося электрического сопротивления рк и потенциала собственной поляризации исп по всему вскрытому скважиной разрезу пласта. На рис. 35 показаны характерные кривые рк и исп, построенные на основе промыслово-геофизических исследований в стволе скважины в пределах рассматриваемого пласта.
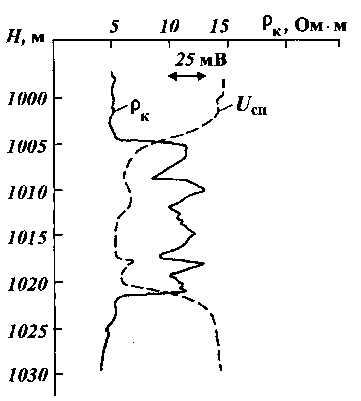
Рис. 35. Кривые рк и U сп, построенные на основе промысловогеофизических исследований в стволе скважины в пределах рассматриваемого пласта
3. В этих же скважинах отбирают образцы пород, слагающих изучаемый пласт. Проводят лабораторные, так называемые петрофизические исследования, в результате которых определяют пористость, абсолютную и относительные проницаемости пород, а также их водонефтенасыщенность.
4. Строят зависимости физических параметров изучаемых пород (пористости, проницаемости, насыщенности нефтью и водой) от промыслово-геофизических параметров (кажущегося сопротивления, потенциала собственной поляризации и др.). Если такие зависимости коррелируются, то физические параметры пород отдельных прослоев определяют только на основе промыслово-геофизических данных. На рис. 36 показана зависимость приращения потенциала собственной поляризации Дисп от ink (где к - абсолютная проницаемость). Зная AUсп по промыслово-геофизическим измерениям в скважинах, можно определить абсолютную проницаемость отдельных прослоев пласта.
5. На основе геологического и геофизического изучения пласта с использованием методов корреляции строят его структурную карту, карты толщин, распространения пропластков, пористости и проницаемости. В результате этих построений оказывается возможным в каждой точке пласта определить все необходимые для компьютерного счета характеристики пласта, которые представляются только в количественном виде, т.е. “оцифровываются”.
6. Выбирается размерность гидродинамической задачи разработки пласта. Если это решается в настоящей трехмерной постановке, то требуется знание свойств пород-коллекторов в каждой точке объема пласта. Задачи часто решаются в квази-трехмерной постановке, когда отдельной точке горизонтальной проекции пласта придаются свойства пласта, изменяющиеся над данной точкой в вертикальном направлении.

Рис. 36. Зависимость прираще ния потенциала собственной по ляризации Дисп от lnk пластков и т.д.) и вычислительной возможности компьютера.
8. Свойства пласта, полученные в результате геологогеофизических и гидродинамических исследований, вводятся в количественном виде в компьютер, и осуществляется решение поставленной задачи с использованием соответствующей вычислительной программы.
ПОСТРОЕНИЕ МОДЕЛИ
СЛОИСТО-НЕОДНОРОДНОГО ПЛАСТА
Эта модель основана на использовании в общих чертах той же процедуры, которую применяют и при построении адресной модели пласта.
После изучения свойств отдельных прослоев пласта осуществляют следующие действия.
1. Заполняют таблицу, в которой отмечают толщину A h отдельных пропластков с абсолютной проницаемостью в пределах Дк;.
2. По данным, указанным в таблице, находят общую толщину h = 2Ah, всех изученных прослоев.
h
3. Определяют доли общей толщины 2Ahi всех пропластков
i=i
с проницаемостью к; или проницаемостью, изменяющейся в некотором сравнительно небольшом диапазоне Ak;.
4. Строят гистограмму проницаемости в виде
_Ah_
f (ki)Aki.
n
2 Ahi i =1
5. Принимают гистограмму за вероятностно-статистическую плотность распределения и для нее подбирают соответствующую аналитическую зависимость.
Необходимость представления гистограмм, построенных по промысловым данным в виде графиков плотностей распределения, аппроксимируемых аналитически, связана, во-первых, с тем, что каждому типу пластов соответствует свой вид плотности вероятностно-статистического распределения. Зная, например, что изучаемый пласт относится к какому-либо известному типу, можно в принципе по нескольким точкам построить график плотностей распределения проницаемости. Это ускоряет процесс создания модели пласта, особенно в начальный период его изучения, когда фактических измерений параметров пласта еще недостаточно.
Во-вторых, аналитическое представление плотности распределения параметров пласта дает возможность при использовании сравнительно простых моделей процессов извлечения нефти из недр аналитически определять показатели разработки пласта.
Наконец, аналитическое представление плотностей распределения промысловых параметров позволяет использовать важные представления математической теории вероятности для того, чтобы лучше характеризовать ими пласты.
6. Включают в модель разработки пласта вероятностностатистические характеристики модели слоисто-неоднородного пласта и получающиеся показатели извлечения нефти из недр сопоставляют с фактическими показателями начальной разработки пласта. В случае несоответствия теоретических и фактических данных разработки вероятностно-статистические характеристики изменяют до получения совпадения теоретических и фактических показателей разработки пласта, т.е. модель пласта адаптируют к фактическому процессу разработки.
ПОСТРОЕНИЕ МОДЕЛЕЙ ТРЕЩИНОВАТОГО
И ТРЕЩИНОВАТО-ПОРИСТОГО ПЛАСТОВ
Существенное влияние трещин, имеющихся в пласте, на процессы его разработки может подтверждаться целым рядом факторов. К одному из наиболее важных из них относят несоответствие фактической проницаемости пласта, определенной по индикаторным кривым или кривым восстановления давления, и проницаемости образцов пород, извлеченных из продуктивного пласта при его разбуривании. Если фактическая проницаемость пласта выше проницаемости отобранных из него образцов пород, то обычно считают, что увеличение проницаемости связано с наличием трещин в пласте. Однако при этом необходимо учитывать, насколько полно представлен изучаемый пласт образцами пород, так как может оказаться, что образцы пород не отобраны из наиболее проницаемых пропластков. Трещиноватость пласта играет значительную роль в процессах его разработки и в тех случаях, когда породы, слагающие пласт, сами по себе достаточно проницаемы, т.е. пласт в целом трещиновато-пористый. Для характеристики установившегося течения в трещиноватом и трещиновато-пористом пластах однородной жидкости достаточно знать только проницаемость пласта, определенную на основе промысловых исследований, и его эффективную толщину. Модель пласта в этом случае строят просто. Однако при неустановившемся течении однородной жидкости в трещиноватом пласте необходимо знать параметры, характеризующие деформацию трещин, а для трещиноватопористого пласта в принципе нужно знать средний размер блока пород или густоту трещин. Эти же параметры учитывают при расчетах процессов вытеснения нефти из пластов различными агентами. Густота трещин - трудно определяемый параметр трещиноватых и трещиновато-пористых пластов. Для ее установления используют данные промыслово-геофизических исследований разрезов скважин (электрических, ядерных и температурных измерений), глубинного дебитометрирования и фотогр афирования.
При исследованиях скважин, например, глубинными дебито-мерами, число отметок в разрезе продуктивного пласта, где происходит резкое нарастание дебита жидкости, считают равным числу открытых трещин, по которым происходит приток жидкости в скважину. Разделив “число случаев” резкого нарастания дебита на суммарную изученную толщину разреза продуктивного пласта, можно оценить среднюю густоту трещин.
Наконец, при построении модели трещиноватого и трещиновато-пористого пластов используют данные о разработке месторождения в начальной стадии.
ПОСТРОЕНИЕ МОДЕЛИ ОДНОРОДНОГО ПЛАСТА
Главные параметры модели однородного пласта - пористость, абсолютная проницаемость и эффективная толщина. Для определения этих параметров проводят промыслово-геофизические исследования пластов в скважинах (определение кажущегося электрического сопротивления нефтегазоносных пород, потенциала собственной поляризации, акустических и ядерных параметров горных пород, потенциала собственной поляризации, акустических и ядерных параметров горных пород, нефти и газа, температуры пласта и др.). Одновременно на кернах, отобранных из продуктивного пласта в этих же скважинах, определяют пористость и абсолютную проницаемость, а также нижний предел проницаемости, т.е. значение проницаемости отдельных пропластков, из которых невозможен промышленный приток нефти или вообще невозможно извлечение нефти в промышленных масштабах при используемой технологии разработки пласта. Далее устанавливают связь между данными непосредственных лабораторных измерений пористости и абсолютной проницаемости и промыслово-геофизическими параметрами. Если такая связь подтверждается, то в дальнейшем пористость и абсолютную проницаемость определяют только на основе данных промысловогеофизических измерений, по результатам которых устанавливают и нефтенасыщенную толщину в скважинах. Из общей нефтенасыщенной толщины пласта вычитают часть толщины пласта с проницаемостью, равной или меньшей нижнего предела проницаемости, и таким образом получают эффективную толщину пласта.
По данным о пористости, абсолютной проницаемости и эффективной толщине, определенных в отдельных скважинах, вычисляют средние значения этих величин для пласта в целом. Особым образом устанавливают относительные проницаемости для модели однородного пласта. Используют так называемые модифицированные относительные проницаемости, методика построения которых будет рассмотрена ниже.
§ 9. МОДЕЛИРОВАНИЕ ПРОЦЕССОВ РАЗРАБОТКИ
Научно обоснованное применение каждого нового процесса разработки нефтяных месторождений начинают с его экспериментального изучения в лабораторных условиях. Все существующие процессы извлечения нефти и газа из недр вначале были изучены при лабораторных исследованиях. В свое время прошло эту стадию и такое широко развитое на практике воздействие на нефтяные пласты, как заводнение. За стадией лабораторного исследования следуют первые промышленные испытания процессов. В этот период развития технологических процессов становится весьма необходимым их количественная формулировка, т.е. создание моделей.
Центральный этап моделирования - постановка соответствующих процессу разработки нефтяного месторождения математических задач, включающих дифференциальные уравнения, начальные и граничные условия. Процедуры расчетов на основе моделей называют м е т о д и к а м и р а с ч е т о в .
Дифференциальные уравнения, описывающие процессы разработки нефтяных месторождений, основаны на использовании двух фундаментальных законов природы - з а к о н а с о -х р а н е н и я в е щ е с т в а и з ак он а с ох р а н е н и я э н е р г и и, а также на целом ряде физических, физико-химических, химических законов и специальных законах фильтрации.
Дифференциальные уравнения будут рассмотрены при изложении соответствующих технологий извлечения нефти и газа из недр. Здесь рассмотрим вопросы использования только фундаментальных законов, а также законов фильтрации, применяемых в той или иной степени во время моделирования всех процессов разработки нефтяных месторождений.
Закон сохранения вещества в моделях процессов разработки месторождений записывают либо в виде дифференциального уравнения неразрывности массы вещества, именуемого часто просто уравнением неразрывности, либо в виде формул, выражающих материальный баланс веществ в пласте в целом. В последнем случае закон сохранения вещества используют непосредственно для расчета данных процессов разработки месторождений, а соответствующий ему метод расчета получил название м е тода материального баланса.
Выведем вначале уравнение неразрывности массы вещества при его одномерном прямолинейном движении в пласте. Масса AM вещества плотностью р в элементе пласта (рис. 37) длиной Ax, толщиной h и шириной Ь, измеряемой в направлении, перпендикулярном к плоскости, при пористости пласта m AM = pmhbAx. (II.38)
Если считать, что в элемент пласта через его левую грань поступает вещество с массовой скоростью pvx, вытесняется из
Ax, а накопленный
элемента с массовой скоростью pvx
объем его SAM за время At, то получим с учетом того, что элемент вошло больше вещества, чем из него вышло:
pvxbhAxAt - (pvx + ^^Vx-)bhAxAt = SAM = A(pm)bhAx.
(II.39)
dx
Из (II.39) имеем
(II.40)
0.
d(pvx) + A(pm)
At
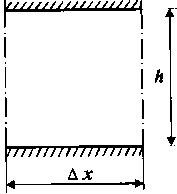
Рис. 37. Схема элементарного объема прямолинейного пласта
dx
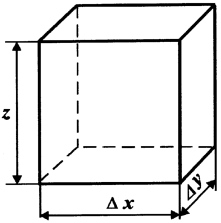
Рис. 38. Схема элементарного объема пласта в трехмерном случае
dx dt
Уравнение (II.41) и есть уравнение неразрывности массы вещества в пласте при одномерном прямолинейном движении насыщающего его вещества. Чтобы получить такое уравнение для трехмерного случая, необходимо рассмотреть баланс массы в объемном элементе пласта AV = Ax Ay A z (рис. 38). Рассматривая массовые скорости поступления вещества в куб и вытеснения из него, а также накопленный объем его в кубе, получаем
-^ + -у- + -L. +
¦d(mp) = 0. (II.42)
dx dy dz dt
Уравнение (II.42) можно записать также в следующем общем виде:
^(mp) = 0. (II.43)
div(pv)
dt
Уравнения (II.42), (II.43) - уравнения неразрывности массы вещества во время его движения при трехмерном измерении. Если в пласте одновременно движутся несколько веществ, находящихся как в газовой, так и в жидкой фазе, составляют уравнения неразрывности массы каждого вещества (компонента) в соответствующих фазах.
Закон сохранения энергии используют в моделях разработки нефтяных месторождений в виде дифференциального уравнения сохранения энергии движущихся в пластах веществ. Полная энергия единицы массы пласта Еп состоит из отнесенных к единице массы внутренней удельной энергии пород пласта и насыщающих его веществ ип, удельной потенциальной z и кинетической энергии веществ, движущихся в пласте со скоростью w. Поэтому
Еп = Un + z + w2/(2g). (II.44)
Из закона сохранения энергии или, точнее, из первого начала термодинамики следует, что изменение энергии пласта AEn и произведенной удельной работы SW равно количеству подведенного к пласту тепла SQX, умноженного на механический эквивалент тепла А, т.е.
A i Uq + z + — i p+ SW = A SQ q
Дадим количественную оценку входящих в (II.46) величин. Удельная внутренняя энергия пласта ип при отсутствии в нем химических или ядерных превращений вещества представляет собой тепловую энергию в единице массы пласта, так что
(II.47)
AU q = AcAT,
где с - удельная теплоемкость пласта; T - температура. Положим, что пористый пласт насыщен водой. Тогда с = ст(1 - m) + + c,m (ст - удельная теплоемкость пород пласта; с, - удельная теплоемкость воды, m - пористость). Пусть с т = = 1,046 кДж/(кг • K), св = 4,184 кДж/(кг • к), A T = 1 K, m = = 0,2. Тогда с = 1,046 • (1 - 0,2) + 4,184 • 0,2 = 1,67 кДж/(кг х х K), AUd = 102 • 1,67 • 1 = 170 м. Удельная потенциальная энергия z в пластах может изменяться в соответствии с возможными изменениями уровня движущихся в пласте веществ. Обычно это десятки и иногда сотни метров.
Оценим возможные изменения удельной кинетической энергии. Скорость w движения в пласте насыщающих его веществ изменяется в значительных пределах - от 0 до 10 м/сут = 3650 м/год = 1,16 • 10-4 м/с. Сравнивая удельные потенциальную и кинетическую энергии пласта с его удельной внутренней энергией, необходимо учитывать, что выше вычислялась удельная внутренняя энергия пласта в целом, т.е. пород и насыщающих их веществ. Удельная потенциальная и удельная кинетическая энергия относятся только к насыщающим пласт веществам. Поэтому с целью указанного сравнения необ-
p m
ходимо ввести коэффициент е
-‘-, где px - плот-
p.m + pD(1 - m)
ность горных пород; p,, - плотность насыщающих пласт веществ; и умножить все виды удельной энергии, кроме внутренней, на е. При p„ = 103 кг/м3, px = 2,25 • 103 кг/м3 m = 0,2, е = = 0,1.
Тогда для изменения удельной кинетической энергии получим
( w2 + 0,1(1,16 • 10 4)2
![]()
= 0,68 • 10-10 M.
Из приведенной оценки следует, что удельной кинетической энергией движущихся в пласте веществ можно всегда, кроме
особых случаев движения веществ в призабойной зоне скважин, пренебречь.
Если изменение удельной потенциальной энергии движущегося в пласте вещества составляет даже 100 м, то при умножении этой величины на е получим 10 м. Изменение же температуры пласта всего на один градус равнозначно изменению удельной внутренней энергии почти на 200 м. Если разработка пласта ведется с использованием тепловых методов, то температура пласта может изменяться на сотни градусов, и его удельная внутренняя энергия станет преобладающей среди других видов энергии. Оценим возможную величину работы, которую могут производить насыщающие пласт вещества. Удельную работу SW, производимую насыщающим пласт веществом и отнесенную к единице массы вещества, определим следующим образом:
S W = pSAV /(pgAV),
(II.48)
где р - давление; AV - объем вещества, насыщающего пласт в элементарном объеме пласта; p - плотность этого вещества; g -ускорение свободного падения.
Поровый объем пласта остается, вообще говоря, неизменным, поскольку практически мало изменяются геометрия пласта и его пористость. Работа вещества в пласте связана всегда с его расширением. Поэтому в (II.48) введена величина SAV, характеризующая расширение вещества. При этом условно можно считать, что вещество, насыщающее пласт, расширяясь, как бы выходит за пределы элементарного объема пласта. Будем считать, что при бесконечно малом расширении вещества в элементарном объеме пласта масса вещества AM = pAV остается неизменной.
Тогда SAM = SpAV + pSAV = 0 и, следовательно,
(II.49)
SAV/AV = -Sp/p.
Подставляя (II.49) в (II.48), получаем
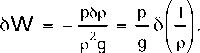
(II.50)
Оценим возможную работу вещества, насыщающего пласт. Очевидно, что наибольшую работу может производить в пласте газ. Для простоты оценки будем считать газ идеальным, для которого p/p = p0/p0, где p0, p0 - давление и плотность газа при начальных условиях. Отсюда для идеального газа
eSW = --eP° ^. (II.51)
p0g p
Пусть при снижении давления Sp = -10 • 105 Па, p = 100 х х 105 Па, p0 = 105 Па, p0 = 1 кг/м3, е = 0,1.
Тогда
eSW = 0’
1 ^10 5 ^10 ^ 105 = 102
M.
1 • 9’ 81 • 100 • 105
Сделанная оценка показывает, что работа вещества, насыщающего пласт, хотя и намного меньше, чем изменение удельной внутренней энергии при тепловых методах разработки нефтяных месторождений, все же при определенных условиях, как это показывает опыт, может быть значительной.
Рассмотрим вопрос о том, чему равняется входящая в (II.45) и (II.46) величина SQX. Изменение количества тепла в элементе пласта может происходить за счет экзотермических химических реакций, гидравлического трения и за счет теплопроводности. Выделение тепла из элемента пласта за счет теплопроводности в дальнейшем будем учитывать при изменении внутренней энергии пласта UD. Перенос тепла из пласта в кровлю и подошву будем учитывать соответствующими граничными условиями и поэтому в балансе энергии элементарного объема пласта его не будем принимать во внимание. Энергия движущегося в пористой среде вещества за счет гидравлического трения превращается в тепло. Для мощности гидравлического трения, отнесенной к единице массы движущегося вещества в элементе пласта, имеем следующее выражение:
2
AN = —v
gradp = . (II.52)
pgAV0 mpg mpgk
Допустим, что в пласте движется газ вязкостью ^ = 0,02 х х 10-3 Па • с со скоростью w = 10-6 м/с « 86,4 • 10-3 м/сут. Проницаемость пласта k « 0,1 мкм2, по ристость m = 0,2, плотность газа p составляет 1 кг/м3.
Тогда
^v2 0,02 • 10-3 • 10-12 -6 ,
- = 1,02 • 10 м/с.
mpgk 0, 2 • 10 13 • 981
В сутки из 1 кг движущегося в пласте газа будет выделяться 1,02 • 10-6 • 0,864 • 105 = 0,088 кг-м/кг энергии. Это, конечно, небольшое значение. Однако, например, в призабойной зоне скважин скорость фильтрации того же газа может достигать 10-4 м/с и более. Тогда при тех же остальных условиях, что и выше, ^v2/(mpgk) ~ 10-2 м/с. В сутки из 1 кг фильтрующегося в пласте газа выделится энергии почти 9 кДж. Таким образом, можно заключить, что наиболее существенное изменение энергии в элементе пласта связано с переносом тепла за счет теплопроводности и конвекции. Определенный вклад в энергетический баланс пласта, особенно при высоких скоростях движения насыщающих его веществ, вносят работа расширения-сжатия веществ и гидравлическое трение.
Напишем уравнение сохранения энергии в пласте, учитывая теплопроводность и конвекцию, а также работу расширения-сжатия веществ и гидравлическое трение.
В соответствии с (II.48) и (II.49) работу движущегося вещества в элементарном объеме пласта в целом можно представить в следующем виде:
SW' = mSW = mp
5AV = -mp —. (II.53)
pgAV p2
Работу W' можно приравнять к энергии сжатия Ep, поэтому p2 psp
SW' = - mSEp = m/^f, (II.54)
p1 p
где p1 и p2 - плотности.
Рассматривая, как и при выводе уравнения неразрывности массы фильтрующегося в пласте вещества, поток внутренней энергии u = cpT и энергии сжатия Ep, а также считая, что тепло поступает в элементарный объем только за счет гидравлического трения, т.е. что ASQX = v gradp, получаем
a(— + divvEu| + ml p
p + divEnvi = vgradp. (II.55)
) at ,
Здесь vE - вектор суммарной скорости теплопереноса в пласте за счет теплопроводности и конвекции; v - вектор скорости фильтрации. Выражение (II.55) и есть дифференциальное уравнение сохранения энергии в пласте, выведенное при указанных выше предположениях.
Рассмотрим законы фильтрации. Основным законом подземной гидромеханики является закон фильтрации однородной жидкости или газа - з а к о н Д а р с и . Все известные законы фильтрации базируются на этом основном законе.
kkH(s) dpн
kkB(s) dpB
ax
vB = -
. (II56)
M H dx M B
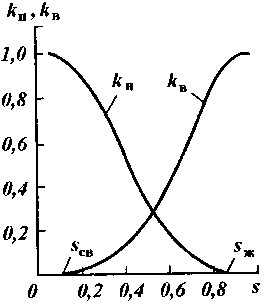
где vK - вектор скорости фильтрации нефти; v в - вектор фильтрации воды; kK(s), k^S), kв(S) - относительные проницаемости соответственно для нефти и воды, зависящие от водонасыщенности s; pK и p в - давление соответственно в нефти и воде. Графики относительных проницаемостей для нефти и воды имеют вид, показанный на рис. 39, на котором по оси абсцисс отмечены две характерные точки: s^ и s,. В точке s = s^ относительная проницаемость для воды равна нулю, так что k^s^) = = 0. В точке s = s, относительная проницаемость для нефти kK(s,) = 0, несмотря на то что в точке s = s^ в пласте присутствует вода, а в точке s = s, имеется нефть. Однако при s = s^ вода, содержащаяся в пористой среде пласта, диспергирована, раздроблена или, если это связанная вода, занимает преимущественно углы между зернами породы, тупиковые поры и т.д. Нефть, имеющаяся в пласте при s = s,, также диспергирована, занимает в пористой среде тупиковые места и вытесняться из пласта не может. Аналогичные зависимости можно построить и для двухфазной фильтрации жидкости и газа. Одновременная фильтрации нефти, воды и газа изучена в меньшей степени, чем совместная фильтрация двух из этих веществ. При расчетах процессов разработки нефтяных месторождений, в которых возникает одновременная фильтрация нефти, воды и газа (трехфазная фильтрация), можно пользоваться следующим приемом. Вначале берут относительные проницаемости при двухфазной фильтрации жидкости (нефти и воды) и газа, для которой известны зависимости относительных проницаемостей
При фильтрации неоднородной жидкости или смесей жидкости и газа справедлив закон двухфазной фильтрации. В случае, например, совместной фильтрации нефти и воды формула закона фильтрации для прямолинейного движения записывается в следующем виде:
Рис. 39. Графики зависимости кн и к в от s с и s,
vH = -
для газа и жидкости kr(sr) и кж(эж) от насыщенности пористой среды газом s„ и жидкостью s^ Поскольку
s„ + sж = 1; ^ = s, + sh> (II57)
где Sв, sh - соответственно насыщенности пласта водой и нефтью, можно написать следующие выражения:
ss
= 1; s = sB/ sж. (II.58)
^ Зж
Затем учитывают уже относительные проницаемости для нефти kH(s) и воды kв(s), определяя s из (II.58). Таким образом, формула закона совместной фильтрации газа, нефти и воды (многофазной фильтрации) принимает следующий вид:
v = - kkr(sr) dpr . v = - kkж(sж)kн(s) p .
г MГ dx ’ н Mн dx
v = - kkж^ж)kB(s) dpв (II 5g)
M H dx
Здесь рг, рн, рв - давление соответственно в газе, нефти и воде. Во многих случаях на движение в пласте веществ существенное влияние оказывает гравитационное поле Земли - сила тяжести. Влияние этой силы на разработку месторождений необходимо
учитывать при движении в пласте разнородных веществ, зна
чительно отличающихся по плотности (например, нефти и газа); большом наклоне или значительной толщине пластов; разработке нефтяных залежей, подстилаемых водой; образовании водо- и газонефтяных конусов и т.д. Поскольку сила тяжести имеет вертикальное направление, она не влияет на горизонтальные компоненты скорости фильтрации, а воздействует только на вертикальную компоненту. При двухфазной фильтрации газа и нефти с учетом гравитации используют следующие выражения для вертикальных компонент скорости фильтрации нефти и газа:
где р - давление, принимаемое одинаковым в газовой и нефтяной фазах.
Во всех рассмотренных случаях скорость фильтрации пропорциональна градиенту давления, т.е. она линейно зависит от градиента давления. Известны также нелинейные зависимости скорости фильтрации от градиента давления. Соответствующие законы фильтрации называют нелинейными законами фильтрации. Нелинейность законов фильтрации обычно связывают с тремя причинами: с проявлением инерционных сил при повышенных скоростях фильтрации, с деформацией горных пород
и, как следствие, с линейным изменением проницаемости пород пласта от давления, а также с неньютоновскими свойствами движущихся в пласте веществ. При этом нелинейная связь скорости фильтрации и градиента давления свойственна только нелинейным законам, обусловленным действием инерционных сил и проявлением неньютоновских свойств насыщающих пласт веществ. Нелинейность закона фильтрации, вызванная деформацией горных пород, есть скорее проявление нелинейной зависимости проницаемости пород от давления. Вначале рассмотрим нелинейность закона фильтрации, связанную с проявлением инерционных сил. Экспериментально было обнаружено, что даже во время фильтрации однородной жидкости при повышенных числах Рейнольдса NRe = vd^/м (v - скорость фильтрации; р, м - соответственно плотность и вязкость фильтрующего вещества; dn - характерный “внутренний” линейный размер пористой среды, например, средний диаметр пор) наблюдается отклонение от закона Дарси. Критические числа Рейнольдса для пористой среды, при которых происходит нарушение закона Дарси, составляют от 7,5 до 9,0 по
Н.Н. Павловскому, от 0,22 до 0,29 по М.Д. Миллионщикову и от
1 до 12 по В.Н. Щелкачеву. Эти критические числа Рейнольдса различны вследствие того, что указанными авторами принималось разное значение dD. Эксперименты показывают, что при числах Рейнольдса, больших, чем критические, градиент давления пропорционален квадрату скорости фильтрации. При числах же Рейнольдса меньше критических, когда справедлив закон Дарси, градиент давления линейно зависит от скорости фильтрации. Естественно, возникла мысль объединить закон Дарси и закон квадратичной зависимости градиента давления от скорости фильтрации. Этот объединенный закон получил н аз в а н и е д ву чл е н н о го з ак он а ф и л ь т р а ц и и , формула которого имеет следующий вид:
k 2 3p
M dx
где a - коэффициент, определяемый экспериментальным путем.
Квадратичная зависимость скорости фильтрации от градиента давления практически может наблюдаться только при фильтрации газа в призабойных зонах или при фильтрации нефти в породах с чисто трещинной пористостью.
§ 10. СВОЙСТВА ГОРНЫХ ПОРОД, ПЛАСТОВЫХ ЖИДКОСТЕЙ И ГАЗОВ
Свойства как горных пород, так и пластовых жидкостей и газов определяют прежде всего путем исследования глубинных образцов пород-кернов, отобранных из пластов во время бурения скважин, а также жидкостей и газов, поднятых с забоев скважин. Однако эти свойства можно определить и путем обработки данных о физических, физико-химических, гидродинамических и механических процессах, происходящих в пластах при их разработке, а также при геофизических, гидродинамических и других исследованиях. При расчетах процессов разработки нефтяных месторождений требуются не только те свойства горных пород, жидкостей и газов, которыми они обладали в начальном состоянии пласта, но и какими они могут обладать в изменившихся условиях при осуществлении методов извлечения углеводородов из недр. Поэтому свойства горных пород, жидкостей и газов познаются не путем проведения простых “определительских” работ, а в результате исследований.
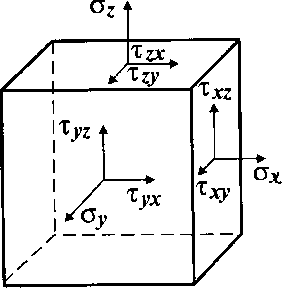
Горные породы, залегающие в земной коре, и в том числе породы, слагающие нефтегазоносные пласты, находятся в напряженном состоянии. Если представить элементарный объем горных пород в виде куба (рис. 40) с гранями dx, dy, dz, то напряженное состояние такого элементарного объема пород будет характеризоваться тензором напряжений с шестью компонентами ax, ay, az, Tyz, тху, Txz (ax, ау и az - нормальные, а тху, Tyz,
Txz - касательные компоненты напряжения). Если ось z направлена по вертикали, x и у - по горизонтали, то нормальное напряжение az = рг
Рис. 40. Компоненты тензора напряжений в элементарном объеме горных пород
характеризует горное или геостатическое давление. Компоненты ax и ay отражают так называемое боковое горное давление, обозначаемое как a6. При равномерном распределении бокового горного давления ax = ay = a6. Считается, что при сравнительно пологом залегании пластов вертикальное горное давление
aF = уЫ. (II.61)
Здесь y - удельный вес вышележащих горных пород, Н/м3; Ы - глубина залегания пласта. Для бокового горного давления
ae = a aF, (II.62)
где a - коэффициент бокового горного давления. Этот коэффициент может изменяться в широких пределах (чаще всего
0 < a < 1), но может и превышать единицу при наличии сильных тектонических напряжений, действующих в боковом направлении. Рассмотренное напряженное состояние свойственно непористым и непроницаемым породам. В нефтегазоносных пластах напряженное состояние горных пород будет несколько более сложным. Дело в том, что нефтегазоносные пласты пористые, насыщенные жидкостями или газами, ограничены сверху и снизу непроницаемыми породами. В пласте существует помимо напряжений в горных породах внутрипоровое давление р, создаваемое жидкостью или газом.
Напряженное состояние характеризуется с р е д н и м н о р -м а л ь н ы м н а п р я ж е н и е м a, которое определяют по формуле
a = (a х + a y + a z) / 3. (II.63)
Между вертикальным горным давлением aT, средним нормальным напряжением a и внутрипоровым давлением р существует связь
aT = a + р. (II.64)
Экспериментально доказано, что такие важнейшие свойства горных пород-коллекторов нефти и газа, как пористость m и абсолютная проницаемость к, зависят от среднего нормального напряжения, причем эти зависимости при широком диапазоне изменения a нелинейны. На рис. 41 показана зависимость пористости m от a, а на рис. 42 - проницаемость к от a. С увеличением a значительно уменьшаются как пористость, так и проницаемость. При этом принимаем, что если a = a0, то m = m0, к = к0 (m0, к0 - соответственно начальные значения пористости и проницаемости). Пористость и проницаемость вначале резко уменьшаются с увеличением a, а затем их уменьшение замедляется (см. рис. 41, 42). Такое существенно нелинейное измене-
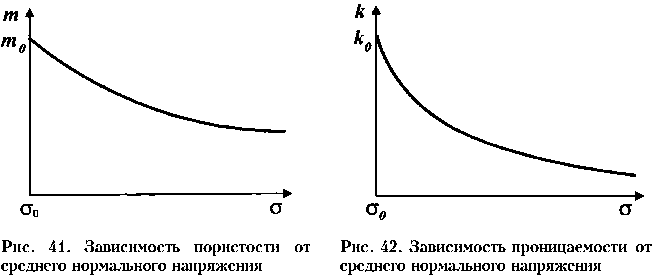
ние m и к происходит у горных пород при До = а0 - о, исчис
ляемых обычно несколькими десятками мегапаскалей. Во многих же внутрипластовых процессах, например, вдали от призабойных зон скважин при упругом режиме, изменение среднего нормального напряжения составляет единицы мегапаскалей. В других же случаях, например при сильных воздействиях на призабойную зону скважин, компоненты напряжения действительно могут изменяться в широком диапазоне, и тогда необходимо учитывать нелинейный характер зависимости пор истости и проницаемости от среднего нормального напряжения.
В случаях больших глубин (свыше 4000 м) и аномально высоких пластовых давлений (p - о г) могут начать проявляться существенным образом свойства пластичности, вязкоупругости или иных реологических свойств горных пород. Режим пласта в условиях проявления неупругих свойств горных пород можно назвать р е о л о г и ч е с к и м р е ж и м о м .
Различают нелинейно упругие и неупругие свойства горных пород. В первом случае деформация пород является обратимой, во втором - горные породы “текут” или существующие в ни х напряжения (компоненты напряжения) изменяются с течением времени, релаксируют, так что при возвращении к прежнему напряженному или деформированному состоянию деформация пород или напряжения не будут прежними. Зависимость пористости от среднего нормального напряжения в случае линейной упругости горных пород имеет вид
m = m0[1 -в c (о-о 0)], (II.65)
где m0 - пористость при о = о0; вс - сжимаемость пород пласта;
о0 - начальное среднее нормальное напряжение.
В случае нелинейной упругости зависимость пористости от среднего нормального напряжения представляют следующим образом:
-Рс(о-а0). (II.66)
При реологических режимах пористость зависит, кроме среднего нормального напряжения а, еще и от времени t. Например, если горные породы являются реологическим телом Максвелла, т.е. вязкоупругим телом, зависимость пористости пород от а и t можно представить в виде
— = -в ^ + л, (ii.67)
л*- 'см ..
dt dt u
г м
где всм и им - соответственно “максвелловские” сжимаемость и вязкость пород. Похожи на указанное, но, может быть, еще более значительны, зависимости абсолютной проницаемости горных пород от среднего нормального напряжения и времени.
Рассмотрим свойства пластовых жидкостей и газов. Пластовые нефть и газ - сложные смеси веществ, главным образом углеводородов. Важную роль в процессах разработки нефтяных месторождений играет вода, содержащаяся в пористых средах пластов. При осуществлении методов повышения нефтеотдачи в пласты закачивают весьма разнообразные вещества, которые не содержались ранее в пластах: двуокись углерода, кислород,
азот и др. При добыче из нефтяного месторождения нефти и газа фазовое состояние насыщающих пласт углеводородов может измениться, например из нефти выделится газ при уменьшении давления. Изменение пластовой температуры также приводит к изменению фазового состояния веществ, насыщающих пласт. При разработке месторождений необходимо знать это фазовое состояние с тем, чтобы количественно прогнозировать отбор нефти, газа и воды из месторождения и управлять процессом его разработки.
При расчете фазового состояния веществ, насыщающих пласт, нефть представляют как смесь ограниченного количества условных компонентов, объединяющих некоторые группы индивидуальных веществ. Наиболее простой и распространенный способ такого представления нефти заключается в разделении ее на два условных компонента: “нефть” и “газ”.
При этом с практически оправданной точностью считают, что в изотермических условиях (T = const) газ как условный компонент растворяется в условной нефти по закону Генри, т.е.
V гр/ VHo = ap, (II68)
где Угр - объем растворенного газа в начальный момент времени, Ун0 - объем дегазированной нефти; a - коэффициент пропорциональности; p - давление.
Если начальное содержание пластовых углеводородов таково, что на объем дегазированной нефти Ун0 приходится ограниченный объем Угр0 растворенного в ней газа, то при некотором давлении рнас весь газ будет растворен в нефти. Это давление называют д а в л е н и е м н а с ыщ е н и я.
Таким образом,
Рнас = УГро/(аУно). (II.69)
Задача расчета фазового состояния пластовых веществ существенно усложняется в неизотермических условиях и при закачке в пласт неуглеводородных веществ. Конечно, фазовое состояние любой многокомпонентной системы можно определить экспериментальным путем в лабораторных условиях. Однако в процессах извлечения нефти из недр состав пластовых веществ, давление и температура могут изменяться не только в пласте в целом, но и от точки к точке. Практически невозможно экспериментально изучить все условия, которые могут сложиться в пластах, и поэтому необходимо уметь рассчитывать фазовые состояния, опираясь на отдельные, “базовые” эксперименты.
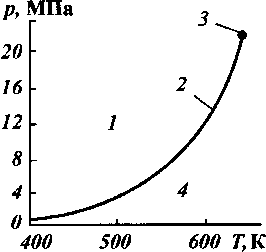
Рассмотрим общие методические основы расчета фазового состояния многокомпонентного вещества, насыщающего нефтяной пласт в неизотермических условиях. В большинстве случаев в пористых средах разрабатываемых пластов находятся две фазы - ж и д к а я и п а р о в а я (газовая). При определенных условиях в поровом пространстве может появиться и твердая фаза -обычно парафин и неорганические соли. Ниже будем рассматривать только двухфазное (жидкость и пар) состояние веществ, насыщающих пласт. При этом начнем с отдельного, индивидуального вещества. Состояние вещества (газообразное, жидкое или одновременно и то, и другое) определяют с помощью диаграммы давление - температура (pT - диаграмма) для данного вещества. На рис. 43 показана такая диаграмма для воды, из которой видно, что в области, находящейся над кривой 2, называемой линией насыщения, вода находится в жидкой, а под ней - в паровой фазе. Точка 3 на кривой 2 называется к р и т и -ч е с к о й . Ей соответствуют критическое давление ркр и критическая температура Ткр. Справа от вертикальной линии, проходящей на диаграмме через критическую точку, и выше проходящей вещество находится в закритическом состоянии. Если давление и температура соответствуют давлению и температуре на линии насыщения, то вещество находится одновременно и в жидкой, и в паровой фазах.
Рис. 43. Диаграмма давление — температура для воды:
1 - область жидкого состояния; 2 - линия насыщения; 3 - критическая точка; 4 - область пара
Если в некотором фиксированном объеме V находится смесь, состоящая из двух индивидуальных веществ, то рГ-диаграмма имеет вид, показанный на рис. 44, где схематично изображена рГ-диаграмма для системы этан - декан. Кривая
1 - линия насыщения для чистого этана, а точка 2 - его критическая точка. Кривая 6 - линия насыщения чистого декана, а точка 5 - его критическая точка. Верхняя огибающая кривая 3 соединяет линию псевдокритических давлений для системы этан - декан при различных содержаниях этих компонентов. Точка, например, 1' соответствует большему содержанию этана в системе, чем точка', а точка 2' - большему содержанию этана, чем точка 3'. Пунктирные линии 4 - псевдолинии насыщения для системы этан - декан также при различных содержаниях этих компонентов. С помощью этих линий можно заменить двухкомпонентную смесь некоторым одним гипотетическим компонентом, имеющим одинаковые с двухкомпонентной смесью критические давление и температуру. Псевдолинии насыщения и псевдокритические давление и температура разделяют области существования жидкой и паровой фаз для двухкомпонентной смеси таким же образом, что и для одного индивидуального компонента.
Для полного расчета давления, насыщенности объема фазами, содержания компонентов в фазах при заданном общем
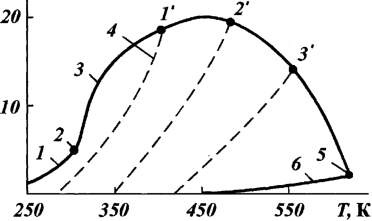
Рис. 44. Диаграмма давление — температура для смеси этана с деканом составе компонентов в объеме и заданной температуре недостаточно использовать только рТ-диаграмму. Необходимо знать также экспериментально определяемые коэффициенты распределения компонентов в фазах. Эти коэффициенты в теории фазовых равновесий известны под названием “константы равновесия”, хотя они по существу для реальных веществ не являются константами. Константой Kip равновесия i-го компонента в смеси из п компонентов называется отношение
Kip = Уг/Хг,
(II.70)
где у{ и xt - молярные доли i-го компонента соответственно в паровой и жидкой фазах. В псевдокритической точке различие между паром и жидкостью исчезает. Поэтому Kip(pu кр, Тп кр) = 1, где рп кр> Ти кр - псевдокритические давление и температура. Из рТ-диаграммы для бинарной смеси (см. рис. 44) видно, что псевдокритические давления и температуры зависят от общего состава смеси и температуры Т. Константы равновесия, т.е. коэффициенты распределения компонентов в паровой и жидкой фазах, зависят от отношения давления к псевдокритическому давлению и отношения температуры к псевдокритической температуре, так что
![]()
(II.71)
В случае многокомпонентной смеси псевдокритическое давление рп кр называют также д а в л е н и е м с х о ж д е н и я . Будем считать, что рассматриваемая смесь веществ состоит из углеводородов, для каждого из которых известны коэффициенты распределения компонентов в паровой и жидкой фазах Kip. Составим уравнения фазовых концентраций. Пусть N - масса всех компонентов в некотором объеме V, N г - масса всех компонентов в паровой фазе (в газе) и N ж - масса всех компонентов в жидкости. Тогда
(II.72)
N = NT + Nx.
Если разделить левую и правую части выражения (II. 72) на сумму молекулярных масс всех компонентов, содержащихся в объеме V, то получим
(II.73)
ni = ni „ + niё ,
где пм - число молей компонентов в объеме; пм г и пм ж - число молей соответственно в газе и жидкости.
Для молярных долей компонентов в газе yt и жидкости xt имеем выражения
/ IVI|
Молярную долю i-го компонента в объеме в целом можно определить следующим образом:
(II.75)
М
Из приведенных выражений получим
V;nM = У;ПМ г + ХПм ж. (II 76)
Учитывая, что yt = Kipxi, а также обозначая пм г/пм = Y, пмКж/п = X, из (II.76) имеем
yi =
J 'K'\ .
(II77)
Y(K|P - 1) + 1 Y(Kip - 1) + 1
Полученные уравнения (II.77) называются у р а в н е н и ям и ф аз ов ых к он ц е н т р ац и й .
При определении фазового состояния можно решать различные задачи. Если, например, заданы v, р, T и Y, то xt и yt определяют непосредственно из (II.77). Если заданы vit р и Т и следует найти Y и X, то с учетом того, что 2х; = 1, из (II.77) получаем
2-v-= 1. (II.78)
Y(Kip - 1) + 1
Значение Y определяют решением уравнения (II. 78).
В том же случае, когда заданы только vt и Т, а нужно определить хг, yt, Y и р, то к уравнениям (II.77) необходимо добавить еще уравнение газового состояния. Для углеводородных компонентов при давлениях и температурах, близких к нормальным, в качестве уравнения газового состояния можно использовать уравнения Редлиха - Квонга, Пенга - Робинсона и других, а при высоких температурах - уравнение состояния идеального газа. В общем случае уравнение газового состояния может быть записано в виде
F(p, V, T) = 0. (II.79)
Система уравнений (II.77) - (II.79) позволяет определить давление р и составы газовой и жидкой фаз. В виду нелинейности уравнений их решение обычно получают методом итераций.
В тех случаях, когда в пористой среде пластов присутствуют неуглеводородные вещества, следует учитывать константы равновесия этих веществ с углеводородами. При отсутствии таковых можно для приближенных расчетов пользоваться представлением о смеси веществ в газовой фазе как о некотором идеальном газе, а также считать, что в жидкой фазе углеводородные компоненты не растворяются в неуглеводородных. Решив основную задачу нахождения хг, yt, Y и р, можно по приведенным формулам определить массу N ж каждого компонента в жидкой фазе. Для того чтобы найти насыщенность s жидкой фазой рассматриваемого объема V, следует использовать значения кажущихся плотностей каждого из компонентов. К а ж у щ е й с я п л о т н о с т ь ю piK называется плотность компонента, когда он растворен в жидкой фазе. Имеем
sV '2L-xi/ргк'
(II.80)
Плотности веществ изменяются с давлением и температурой. Значения плотностей и характер их изменения с давлением и температурой можно найти в специальной литературе.
Важным для разработки нефтяных и газовых месторождений свойством пластовых жидкостей и газов является их в я з -к о с т ь , влияющая, согласно закону Дарси, на темпы извлечения из пласта насыщающих его веществ. Если нефть представляется как смесь индивидуальных углеводородов, имеющих вязкости ^j, то для вязкости нефти цн имеем формулу
и н = ); Ci = Пм| / ^ пм|,
(II.81)
здесь П - произведение вязкостей i-го компонента в степени Q. Допустим, что нефть может быть представлена как смесь из трех условных компонентов - легкого, имеющего вязкость ц и молярную концентрацию Си среднего (основного) с вязкостью [Л2 и молярной концентрацией в смеси С2 и тяжелого, обладающего вязкостью ц3 и молярной концентрацией в смеси С3. При этом
(II.82)
C + с2 + Сз = 1.
Из формулы (II.81) с учетом (II.82) получим
![]()
Вязкость углеводородных компонентов, составляющих нефть, как и вязкость нефти, уменьшается с ростом температуры, причем тем резче, чем больше их начальная вязкость. Вязкость
газов также изменяется с температурой и давлением, хотя и не столь значительно, как вязкость нефти.
Наконец, необходимо указать, что не только горные породы, но и сама нефть может обладать реологическими свойствами, отличающими ее от ньютоновской жидкости. Например, она может характеризоваться предельным напряжением сдвига. Если при фильтрации ньютоновской жидкости справедлив закон Дарси, то фильтрация нефти, обладающей предельным напряжением сдвига, характеризуется законом, предложенным А.Х. Мирзаджанзаде. Формула этого закона имеет вид
v = - - (gradp - д0), (II.84)
и
где д0 - начальный градиент давления. Чтобы началась фильтрация жидкости по формуле (II.84), должно быть соблюдено условие grad р < д0.
Ввиду важности для разработки нефтяных месторождений расчетов фазового состояния пластовых жидкостей и газов рассмотрим пример.
П р и м е р II.2. Допустим, что в некотором замкнутом объеме V содержится N1 килограммов углеводородного компонента 1, т.е. газа, и N2 килограммов компонента 2, т.е. нефти, при стандартных условиях Т = Т0 = const. Будем приближенно считать газ идеальным. Растворимость газа в нефти подчиняется закону Генри. Заранее известно, что содержание углеводородов в объеме V таково, что их смесь находится в двухфазном состоянии, причем содержание второго компонента в газе мало и его можно считать равным нулю. Требуется определить давление р в замкнутом объеме V и его насыщенность s жидкой фазой.
Для жидкой фазы из (II.80) имеем следующее уравнение:
sV = L1/pta + L 2/ р 2к> (II.85)
где L1 - масса первого компонента в жидкой фазе; р1к - его кажущаяся плотность; L2 = N2 - масса второго компонента в жидкой фазе, где он и находится. Масса растворенного в нефти газа
L1 = ^рр01>
где р01 - плотность газа при стандартных условиях. Кроме того,
V„ = L2/р2к ’
где р2к - кажущаяся плотность нефти или плотность дегазированной нефти. Таким образом, из формулы закона Генри (II.68) получим
L1 = ар0^2р/р2к = «р01^р/р2к- (11.86)
По условию газ считается идеальным, а условия являются изотермическими. Тогда плотность газа
рг = р01р/р0’
где р0 - стандартное давление (принимаем р0 = 105 Па). Из приведенного выражения масса газовой фазы
G1 = (1 -
Б)Ург = (1 - з)Ур01Р .
(II.87)
Ро
G1 + L1 = N1.
Подставляя в это выражение (II.85), (II.86) и (II.87), получаем квадратное уравнение
ap2 - bp + c = 0;
a = ар01N2 . ^ = ap01N2p0 + Vp01р2к - ^^2р01 (II 88)
р1кр 2к р0 р2к p 0
Определим параметры рассмотренного фазового состояния. Пусть V = = 1 м3, N1 = 25 1сг, N2 = 500 кг, a = 0,8-10-5 м3/(м3-Па), р1к = 0,2-103 кг/м3, р2к = 0,8-103 кг/м3, р01 = 0,8 кг/м3. Подставив эти цифры в уравнение (II.88), получим а = 1,6-10-13, b = 0,7-10-5, с = 25 (размерности опускаем). Решив квадратное уравнение и опуская один из его корней, не удовлетворяющий исходным условиям, имеем
0,7 -10-5 - (0,33-10-10)1/2 3,2 -10-13
- 39 -105 Па.
p-
Далее получим s = 0,7, L = 15 кг, G1 = 10 кг. Таким образом, задача решена.
Рассмотрим в общем виде другой метод решения этой же задачи, но без предположения о растворимости газа в нефти по закону Генри. Для этого используем коэффициенты распределения компонентов (константы равновесия).
Будем, как и выше, для простоты считать, что второй компонент не переходит в газ, т.е. что G2 = 0. В этом случае в соответствии с формулой (II.71) имеем
![]()
Считая газ идеальным и используя приведенные соотношения, приходим к системе алгебраических уравнений
![]()
![]()
(II.89)
Систему (II.89) необходимо решать методом итераций, получив предварительно зависимость К1р от р/рп 1р, Т/Тп путем аппроксимации экспериментальных данных, а также определив по рГ-диаграмме для двухкомпонентной смеси давление схождения рп и соответствующую ему температуру Т
п KD'
Можно вместо формулы закона идеального газа использовать иные уравнения газового состояния, учитывающие реальные свойства газа. Метод расчета фазового состояния с использованием констант равновесия дает возможность лучше учесть фазовое взаимодействие реальных углеводородов, но он влечет за собой более сложные вычисления.
§ 11. ИСПОЛЬЗОВАНИЕ МАТЕМАТИЧЕСКИХ МЕТОДОВ ПРИ РАСЧЕТАХ РАЗРАБОТКИ
Модель разработки нефтяного месторождения обычно представляется математически в виде системы, состоящей из алгебраических, дифференциальных, интегральных уравнений или соотношений. Для того, чтобы провести расчет на основе уже созданной модели разработки месторождения, необходимо сначала решить соответствующие математические задачи. Только получив решение этих задач, можно осуществлять сам расчет в цифрах.
В § 11 дается на ряде примеров описание основных математических методов, применяемых при решении задач разработки нефтяных месторождений.
МЕТОДЫ ПОЛУЧЕНИЯ ТОЧНЫХ РЕШЕНИЙ ЗАДАЧ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
Многие задачи разработки нефтяных и газовых месторождений сводятся к решению классических уравнений математической физики. В ряде случаев можно получать решения задач математической физики, в точности удовлетворяющие исходным уравнениям, начальным и граничным условиям. Такие решения называются точными. К числу методов, дающих точные решения задач разработки нефтяных месторождений, относится хорошо известный из курса математики метод разделения переменных (метод Фурье), методы функций комплексного переменного, интегральных преобразований, получения автомодельных решений и др.
Методы функций комплексного переменного являются классическими методами решения задач установившейся фильтрации несжимаемой жидкости в плоских пластах. Рассмотрим э ти методы при установившемся притоке жидкости к источникам (скважинам).
1. Уравнение неразрывности массы жидкости, фильтрующейся в плоском пласте, имеет, исходя из (II.42), следующий вид:
dvx + V - 0. (II.90)
dx dy
Подставляя в это уравнение формулу закона Дарси
V, . - k iE ; V _ - k * , (11.91)
^ dx ^ dy
получаем уравнение Лапласа
2 2
Iе + !?. _ 0. (11.92)
dx2 By2
Введем потенциал фильтрации в виде Ф = kp/ц.
В этом случае вместо уравнения (11.92) получим
^ ^ = 0. (11.93)
dx2 By2
Введем комплексный потенциал
F(z) = Ф + iW; z = x + iy. (11.94)
Входящая в выражение (11.94) функция ф = ф(х, у) - функция линий тока. В теории плоского потенциала доказывается, что комплексный потенциал F(z) и функция линий тока удовлетворяют условиям Коши - Римана
дФ _ dW . дФ _ dW (II 95)
dx dy ’ dy dx
Таким образом, любая аналитическая функция комплексного переменного z = x + iy описывает некоторое плоское течение в пласте. Пусть, например,
F(z) _ Ф + iW _ — ln z. (11.96)
2nh
Полагая z = rei0, (0 = arctgy/x), из (11.96) получаем
F(z) _ Ф + iW _ -^- (ln r + i0) _ -^ & ln r + iarctgy|, (11.97)
2nh 2nh ' x *
отсюда
Ф _ — ln r; W _ — arctg y;
2nh 2nh x
r = (x2 + y2)1/2; p _ ln(x2 + y 2)1/2. (11.98)
2nkh
Рис. 45. Схема бесконечной цепочки скважин в плоском пласте:
1 — скважины; 2 — полоса шириной 2о
| У‘ | i. | |||
| ! 1 1 / |
1 | 1 j |
i 12 | i. L ’ „ ^ |
| - 20 | 0 | . * | ||
| щ------ | <—1 | 2—> |
w | |
Из приведенных формул следует, что комплексный потенциал по формуле (II.96) выражает решение задачи установившейся фильтрации жидкости в неограниченном плоском пласте к единственному точечному источнику. Как видно из (11.98), давление при г = =КО стремится к —ю, а при r ^ ю оно также неограниченно возрастает. Тем не менее можно приближенно использовать это решение и для расчета распределения давления в плоском пласте с несколькими источниками конечного радиуса (скважинами), используя то обстоятельство, что уравнение Лапласа
(II.90) линейно и сумма нескольких решений вида (II.98) есть
тоже решение уравнения (II.90).
Допустим, что в неограниченном плоском пласте (рис. 45) по оси 1 располагается бесконечная цепочка источников (скважин). Каждая из скважин находится на расстоянии 2о от соседней. Для того чтобы найти решение задачи о течении жидкости в пласте, достаточно рассмотреть течение жидкости только в одной полосе шириной 2о, расположенной по обе стороны от оси у.
Получить формулу притока жидкости к одному источнику можно было бы путем суммирования бесконечного числа решений типа (II.98) для источников, расположенных на расстояниях 2оп (п = 1, 2, 3...) от рассматриваемого источника, находящегося в начале координат. Однако более компактно это можно сделать, применив конформное преобразование полосы, расположенной в плоскости z = x + iy (см. рис. 45), в неограниченную плоскость комплексного переменного Z = Ч + in. Такое конформное преобразование дает функция
Z = sin —. (II.99)
о
Если обозначить z1 = nz/ о, то
sinz1 = sin(x1 + iy1) = sinx1cosiy1 + cosx1siniy1 = = sinx1chy1 + icosx1shy1;
e-У1
e-У1
shYi = ¦
chyi
2 2 x1 = nx /о; y1 = ny /о.
Таким образом, в плоскости Z = Ч + in имеем Ч =sinx1chy1; n = cosx1shy1;
р = (Ч2 + n2)1/2. (II.101)
При конформном преобразовании, осуществляемом функцией (II. 99), любой точке полосы -о < 1 < о соответствует определенная точка плоскости Z.
Рассмотрим комплексный потенциал F(Z) в плоскости Z, описывающей течение к источнику в этой плоскости. В таком случае
F(Z)
ln Z, Ф
¦ ln р.
2nh
2nh
(II.102)
Можно с достаточным приближением считать, что вместо точечного источника в плоскости Z существует скважина радиусом рс, где потенциал равен Фс. Тогда примем, что на расстоянии рк от центра скважины потенциал равен Фк. Для дебита скважины в плоскости Z можно написать формулу Дюпюи
2пИ(Ф к - Ф с)
(II.103)
q
ln(p к /р с )
Перейдем снова к плоскости z. При больших значениях у течение в полосе —о < 1 < о будет параллельным оси у. Для этой оси из (II. 101) имеем
р « shny / о.
Поэтому можно положить (см. рис. 45)
nL
г nL 1 —
рк “ sh ^ e о .
о 2
Из этого выражения соответственно получим Ырк = nL/о — ln2.
При значительных расстояниях по оси у имеем nz >> о. Тогда можно положить
пу
e а - e а _ пу _ пгс
ПУ
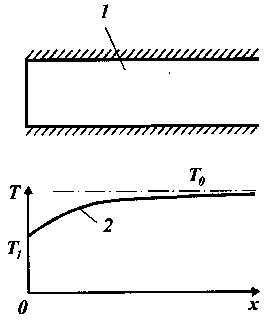
Рис. 46. Схема распространения температуры за счет теплопроводности в полубесконеч-ном стержне:
1 - полубесконечный стержень площадью сечения S; 2 - распределение температуры в стержне в момент времени t
lnpK « пL / а.
При незначительных пу / а
2 а а
Следовательно, lnpc =1п(пгс/а).
Подставляя приведенные значения 1npK и 1прс (II. 104), получаем
формулу (II.104)
2лкИ(рК - рс) _ 2пкИ(рК - pс) _ 2акИ(рК - pс)
ш(1пpк - lnpс)
& пЬ пгс ^ & а т а \
ш--ln-+ ш L + — In-i
1 а а * ' п пгс *
По формуле (II. 104) можно определить дебит одной скважины из бесконечной цепочки скважин, расположенных в неограниченном пласте, при условии, что на некотором, достаточно большом расстоянии z от оси i давление равно рк, а в скважинах малого радиуса гс оно составляет рс.
2. Рассмотрим решение одной из основных задач теории теплопроводности, весьма необходимое при расчетах тепловых методов разработки нефтяных месторождений. Пусть имеем полубесконечный стержень площадью течения S, полностью теплоизолированный от окружающей среды. Начальная температура при t = 0 во всем стержне была равна Т0, а при t > 0 на границе стержня i = 0 (рис. 46) она стала равной Т1, оставаясь при t ^ ю равной Т0. Требуется определить распределение температуры по координате i в различные моменты времени t. Будем исходить из уравнения сохранения энергии, рассматривая теплоперенос в стержне только за счет теплопроводности. Для скорости теплопереноса vT за счет теплопроводности имеем следующее уравнение:
dVT dT г\
дХ dt
Здесь с - удельная теплоемкость вещества в стержне; p -плотность вещества.
Скорость переноса тепла »т за счет теплопроводности можно определить по формуле закона Фурье
эт
vT = -AT —, (II.106)
Эх
где А - коэффициент теплопроводности.
Подставляя (II. 106) в (II. 105), получаем
К T= Я.; к T = ^. (II.107)
Эх2 dt cp
Уравнение (II. 107) есть уравнение теплопроводности при прямолинейном распространении тепла, а входящий в него коэффициент кт называется к о э ф фи ц и е н то м т е м п е р ат у р о -п р о в о д н о с т и . В соответствии с условиями задачи
T = Т0 при i > 0, t = 0; t > 0, x ^ ю,
T = Т1 при x = 0, t > 0. (II.108)
Рассмотрим функцию f(x, t), определяемую следующим образом:
f(x, t) = (T - T>)/(T1 - T0). (II.109)
Тогда начальное и граничное условия (II. 108) запишутся следующим образом:
f = 0 при x > 0, t = 0; t > 0, x ^ ю,
f = 1 при x = 0, t > 0. (II.110)
Функция f(x, t), очевидно, также удовлетворяет уравнению теплопроводности (II.107), как и T(x, t), т.е.
Ко if = f . (II.111)
Эх 2 dt
Для получения решения рассматриваемой задачи применим преобразование Лапласа, для чего умножим левую и правую части (II. 111) на е-й (s - некоторый параметр) и проинтегрируем эти части в пределах от нуля до бесконечности. В результате получим
ю 2с ю с
КT fU-e-stdt = e-stdt. (II.112)
J дv 2 J dt
0 dX 0
Будем считать преобразованием Лапласа функции f(x, t) функцию F(x, s), причем
F(y, s) = J f (у, t)e-stdt. (II.113)
0
Учитывая независимость переменных x и t, функцию f(x, t) можно дифференцировать под знаком интеграла. Из (II. 113) имеем, помня, что s - некоторый параметр,
-\2^ ^ 2f
— = Г— e-stdt (II. 114)
ду 2 0 ду 2
После интегрирования правой части выражения (II. 112) получим
п f ^
Г—e-stdt = | - f (у, t)e-st + s ff (у, t)e-stdt = sF(у, s). (II. 115)
J « 0 -0
Первый член в выражении (II. 115) равен нулю, так как при верхнем пределе он равен нулю в результате стремления к нулю экспоненты, а при нижнем пределе вследствие того, что f(x, 0) = 0 по условию задачи.
После подстановки (II. 115) в (II. 112) получим
kт — - sF = 0. (II.116)
ду 2
Решение обыкновенного уравнения (II. 116) имеет вид
у
F = Ce »Кт . (II.117)
Для установления постоянной интегрирования С выполним граничное условие (II. 110). Однако найдем прежде всего, чему равно F(0, s). Из граничного условия (II.110)
F(0, s) = ff(0, t)e-stdt = /e-stdt = 1 (II.118)
0 0 s
Тогда
у
FU, s) = -e-. (II.119)
s
Функцию f(x, t) по ее изображению F(x, s) найдем по таблицам оригиналов функций и их изображений по Лапласу. Имеем
f (у, t) = 1 - / e-z dz = l - erf! —^j. (II.120)
Получим, наконец, выражение для скорости переноса тепла на границе х = 0. Из приведенного решения с учетом (II.106) находим
у2
4Krt , дт
= Ат ДТ1
е = ;
ДТ1 = Т1 - Т0.
(II.121)
/пкт^у=0 V"KTl
Поток тепла qT через течение стержня площадью S при х =
= 0
qT = Хт^lS . (II.122)
¦JnK т t
3. Рассмотрим приток жидкости (нефти) с постоянным дебитом q к точечному стоку, расположенному в однородном бесконечно простирающемся плоском пласте толщиной h при упругом режиме. Сток находится в центре координат, и течение к нему в пласте радиальное. В начальный момент времени t = 0 пластовое давление постоянно и составляет рк. При t > 0 из точечного стока отбирается из пласта нефть с дебитом q = const, а пластовое давление остается равным рк только при r ^ ». Требуется определить распределение давления в пласте в любой момент времени.
Уравнение неразрывности массы фильтрующегося в пласте вещества имеет в рассматриваемом случае следующий вид:
э(ру) + pv + Э(тр) = 0. (II.123)
дГ Г dt
Учитывая закон Дарси и сжимаемость пласта (сжимаемость пород пласта и насыщающей их жидкости), из (II. 123) получаем уравнение упругого режима в следующем виде:
к & д2р 1 др^ г, др
Ч_2 + “Г I = ;
И ' дГ2 Г дГ * д1
р = Рс + тРж, (II.124)
где Рс и Рж - сжимаемость соответственно пород пласта и насыщающей пласт жидкости. Остальные обозначения такие же, что и принятые выше в формуле закона Дарси. Введем функцию f(r, t) следующим образом:
f = 2пкКрк- р) (II.125)
qn
и подставим ее в уравнение (II. 124). В результате получим K& э— + 1 df_\ = Эр . (II.126)
дГ2Г дГ * dt
Здесь к - пьезопроводность пласта. Поскольку сток точечный (г ^ 0), то для него имеем следующее граничное условие:
q 2nkh&Г др^ q& Э— ^
И \ дГ * 0 \Г дГ * Г^0 .
Следовательно, граничное и начальное условия будут \г—') = -1; f(r, 0) = 0. (II.127)
' дГ* г^0
Известно, что рассматриваемое решение задачи зависит от
одной переменной % = Г / л/Kt. В таких случаях считают, что решение автомодельное, т.е. подобное самому себе. Поэтому f =
= f(%). Имеем
— = -f'—!=; — = f ; — = f "—. (II.128)
dt 2W Kt дГ VKt дГ2 Kt
Подставляя эти значения производных в основное уравнение (II. 126), получаем
и' + — = 0; и = f' %. (II.129)
2
Из (II. 127) имеем следующие условия: f = 0 при % ^
\% —j = -1. (II.130)
' d%*%.0
Решение уравнения (II. 129) получим просто. При выпол
нении условий (II. 130), опуская промежуточные выкладки, полу-
чаем
•% % 2Z z
После подстановки (II. 131) в (II. 125) окончательно имеем
г - z / 2 )
qn г e q^ -I г I
рк - р---^—f—dz---Еп -
4nkh z z 4nkh
'I-- *.
/
2I
Функция -E'i--i положительна при 0 < z < г, но при
z ^ 0 она неограниченно возрастает. Приближенно эту функцию можно использовать для расчета распределения давления при упругом режиме и в случае притока жидкости к источникам малого, но конечного радиуса (г = гс), т.е. к скважинам. Значе-
ф Е-/ Г2 )
ния функции - Е'(--+ можно установить с помощью соответ-
неустановившееся рас-
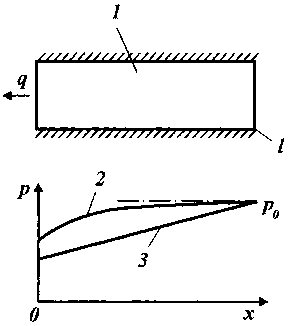
Рис. 47. График перераспределения давления в прямолинейном пласте длиной I при упругом режиме:
1 - пласт;
2 -
пределение давления; 3 - установившееся распределение давления
ствующих таблиц.
4. Пусть имеем прямолинейный однородный пласт толщиной h и шириной b, ограниченный двумя галереями (рис. 47), одна из которых находится в вертикальном сечении i = 0, а другая -в сечении пласта i = l. В начальный момент времени (t = 0) давление во всем пласте было постоянным, равным р0. Это же давление поддерживается постоянным на галерее x = l при t > 0. В момент времени t = 0 из пласта (с галереи i = 0) начинают отбирать нефть с постоянным дебитом q. Пласт разрабатывается при упругом режиме.
Требуется определить распределение давления в описанном ограниченном пласте при t > 0.
Приступив к решению этой задачи, прежде всего отметим, что перераспределение давления в пласте будет описываться тем же по существу уравнением упругого
режима, что и в предыдущей задаче, только в рассматриваемом случае оно будет иметь следующий более простой вид:
к^_р _ Эр . (II.133)
дх2 dt
Для удобства решения задачи введем безразмерные координаты следующим образом:
% = x/l; т = Kt/l2. (II.134)
Подставляя (II. 134) в (II. 133), получаем
d2p / d%2 = dp/Эт. (II. 135)
В соответствии с условиями задачи начальные и граничные условия для уравнения (II. 135) имеют вид
p(%, 0) = p(1, т) = p0; др _ q|il
(II.136)
Э%% _ 0 kbh
Из постановки задачи следует, что при t ^ г распределение давления в пласте будет стремиться к установившемуся
р° - р _ ?(1 -%х (III37)
При % = 0 из (II. 137) циКЬК) = p0 - p1. В связи с приведенным замечанием удобно искать решение задачи в следующем
виде:
p0 - p(%, т) = (p0 - p1)( 1 - %) - (p0 - p1)f(%, т). (II.138)
При этом
f(%, 0) = 1 - %; f(1, т) = 0; (II.139)
% _ 0
При решении этой задачи применим метод Фурье, согласно которому
f(%, т) = ф(т)ф(%). (II.140)
Подставляя (II. 140) в (II. 138) и затем в исходное уравнение (II.135), имеем
ф'ф = ф"ф. (II.141)
ф'/ф = Ф^/Ф = c = const. (II.142)
Решая уравнения (II. 142) и выполняя начальные и граничные условия, приходим к следующему решению задачи:
po - pd, т) = (po - pt)(1 - d -
8(p 0 - Pi) Цx
п2 0 (2n + 1)2
(2n+1)2 п2
2n + 1
4
cos-п?
x e
2
n = 0, 1, 2... . (II.143)
При этом было использовано известное разложение в ряд Фурье:
л & 8 ? 1 2n +1 &
1 - е = — у-cos-пе.
п2 О (2n + 1)2 2
По формуле (II. 143) можно определить время формирования установившегося распределения давления в пласте между двумя галереями (рядами скважин), одна из которых нагнетательная, а другая - добывающая.
ПРИБЛИЖЕННЫЕ МЕТОДЫ
Из приближенных методов расчета в теории разработки нефтяных месторождений наиболее распространены метод эквивалентных фильтрационных сопротивлений Ю.П. Борисова и метод интегральных соотношений Г. И. Барен-блатта. Первый из указанных методов используют при расчете установившихся течений жидкостей в плоских пластах со скважинами, а второй - в расчетах перераспределения давления жидкости при упругом режиме, неустановившегося движения газа и реже - задач диффузии, теплопроводности и конвекции. Метод интегральных соотношений хорошо разработан только для решения одномерных задач.
Рассмотрим вначале метод эквивалентных фильтрационных сопротивлений. Справедливость этого метода покажем на примере конкретного решения о притоке жидкости к бесконечной цепочке скважин. Так, перепишем формулу (II. 104) следующим образом:
1 a ^
П in-
пг.
2akh
Первый член выражения, стоящего в скобках (II. 144), характеризует фильтрационное сопротивление при движении жидкости в полосе шириной 2a на расстоянии от 0 до L, а второй член - фильтрационное сопротивление при радиальном движении жидкости от кругового контура rK = a / п до окружности радиуса гс. Ю.П. Борисов назвал фильтрационное сопротивление nL
внешним, а рФ =n in — /(2ttkh) - внутренним
Р Ф--втеш™, а р ^
Ф 2akh Ф
предположил, что и в более сложных случаях установившихся плоских фильтрационных течений фактические фильтрационные сопротивления можно разделить на эквивалентные внешние и внутренние.
Метод эквивалентных фильтрационных сопротивлений позволяет рассчитывать с достаточной для практики точностью дебиты и давления в пластах при различных системах разработки.
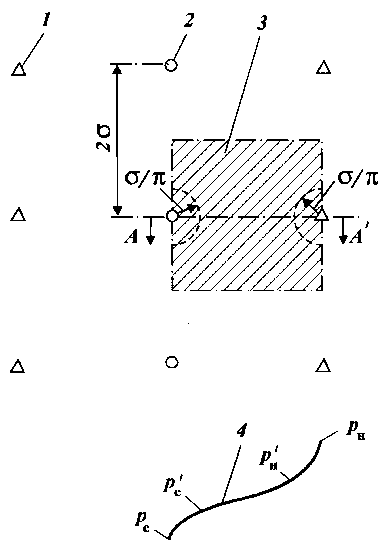
Рассмотрим однорядную систему разработки со схемой расположения скважин, показанной на рис. 48. П ри этом происходит поршневое вытеснение нефти водой из пласта толщиной h. Вязкость нефти в пластовых условиях составляет пн, а вяз-
Рис. 48. Схема распределения давления в элементе однорядной системы разработки:
1 - нагнетательные скважины; 2 - добывающие скважины; 3 - элемент однорядной системы разработки; 4 -
эпюра пластового давления в сечении АЛ'
кость воды nB. Абсолютная проницаемость пласта k, а относительные проницаемости для нефти и воды, являющиеся постоянными согласно модели поршневого вытеснения нефти водой, равны соответственно kE и kB, радиус добывающей скважины гс, радиус нагнетательной скважины гнс. Вода в процессе вытеснения нефти в момент времени t = t1 дошла до расстояния a/п от нагнетательной скважины (см. рис. 48). При этом расстояния между добывающими и нагнетательными скважинами равны. Дебит одной добывающей скважины, равный расходу одной нагнетательной скважины, постоянен и составляет q. Требуется определить перепад давления между нагнетательной и добывающей скважинами.
Рассмотрим течение в одном элементе пласта (см. рис. 48, заштрихованный квадрат) шириной b = 2a. Обозначим давление на расстоянии от нагнетательной скважины, равном rK = a/п, через р'н. В соответствии с условием задачи и формулой Дюпюи
q = ^М^Крн - pН)
n в in
aпггс
Согласно методу эквивалентных фильтрационных сопротивлений течение в рассматриваемом элементе складывается из трех: радиального (течение воды) от нагнетательной скважины радиусом гнс до контура радиусом a/п, прямолинейного (течение нефти) от галереи х = 0, где давление р'н, до галереи x = l, где давление р'с, и радиального (течение нефти) - от контура радиусом a/п, где давление также равно р'с, до добывающей скважины радиусом тс. Учитывая, что ввиду симметрии прямолинейное течение происходит с расходом q/2 (вправо и влево от нагнетательной скважины уходит жидкость с расходом q/2), получаем
q = 2пkkнh(pH - р')
2 П н1
Наконец, для дебита добывающей скважины имеем формулу
q = ^kKh(Pc - Pс)
a
n н1п— пГ
Перепишем приведенные выше выражения относительно перепадов давлений в виде
aa
qnв in--qnн in
i пГнг / / qn Н / пгг
PH-PHPH-Pc=lOkHHh; Pc-Pc=4^
Сложим эти выражения. В результате получим требующийся ответ
п^, 2akH пkн
q
2kh
(II.145)
Рассмотрим ту же задачу, что и (II. 107) - (II. 108), но решим ее методом интегральных соотношений Г. И. Баренблатта, согласно которому приближенное решение задачи представляется в виде многочлена. Далее считаем, что приближенное распределение температуры удовлетворяет не исходному дифференциальному уравнению, а интегральным соотношениям, получаемым в результате умножения левой и правой частей уравнения на координату в степени n и их интегрирования. При использовании описываемого приближенного метода принимают, что всякое незначительное изменение температуры в случае теплопроводности или давления в случае упругого режима распространяется не мгновенно, а существует в ограниченной “возмущенной” области. Для рассматриваемой задачи интегральное соотношение имеет вид
где n - любое, обычно целое число, начиная с нуля. Положим в качестве первого приближения n = 0 и возьмем решение в виде
2
A + A1 — + A2 ——. (II.147)
Ti - i(t) 12(t)
Выполним граничные и начальное условия, которые при приближенном решении задачи имеют несколько иной вид, чем при точном решении, а именно:
T = T0 при 1 = l(t); T = T1 при 1 = 0. (II.148)
Должно также всегда выполняться условие l(0) = 0. При решении задачи приближенным методом необходимо также дополнительно выполнять условие
3x|x=l(t)
Соблюдая приведенные условия, получаем Л = Т1 - То = АТ{; Д = -2АГ1; Аг = АГ1. Таким образом,
2
xx 1 - 2-+
(II.150)
T - То = АТ
l(t) 12(t)
Для определения l(t) подставляем (II.150) в (II.146) при n = 0, считая l1(t) = 0. В результате получим уравнение
6Kxdt = ldl.
Отсюда
l = 2л/ЭК7, (II.151)
т.е. задача решена.
Определим, как и в примере II.4, скорость уноса тепла при
1 = 0. Имеем
vJ x=о = -X т^^ = . (II.152)
dx x = о -v/ЭкTt
Сравнивая приведенное приближенное выражение с точным (II. 122), находим, что скорость уноса тепла, определенная приближенным методом, будет больше точной в --п / Э раз, т.е. всего примерно на 2 %.
ЧИСЛЕННЫЕ МЕТОДЫ
В современных расчетах разработки реальных нефтяных месторождений чаще всего применяют конечно-разностные методы. При использовании этих методов дифференциальные уравнения, описывающие процессы разработки нефтяных месторождений, представляют в конечно-разностной форме. Конечно-разностные уравнения решают с помощью быстродействующих электронно-вычислительных машин-компьютеров. Удобные для использования точные решения задач разработки нефтяных месторождений практически обычно получают только для одномерных случаев (прямолинейное и радиальное течения). При необходимости же рассчитать процессы разработки
Рис. 49. Схема разбиения области со сложной конфигурацией на конечно-разностные ячейки:
1 - контур области; 2 - ячейка А
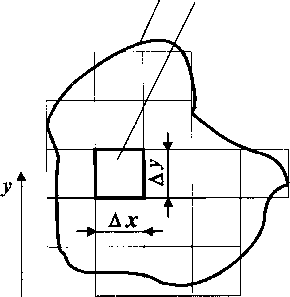
О
х
пластов с учетом их сложной геометрической формы, получить точные и даже приближенные решения не удается. В таких случаях решить задачу можно, применяя численные методы. Например, необходимо рассчитать перераспределение давления в области со сложной конфигурацией (рис. 49) при упругом режиме. В этом двумерном случае уравнение упругого режима имеет вид
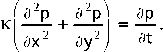
(II.153)
Область течения нефти в плоском пласте разбивается на множество ячеек с размерами А х, А у и h соответственно по осям х, у и z. Рассмотрим ячейку А, которая при бесконечном дроблении (А X ^ 0, А у ^ 0) превращается в точку А. Будем считать, что в этой ячейке давление равно pПри замене в уравнении (II. 153) бесконечно малых приращений конечными выражения для производных преобразуются следующим образом
dp . + 1j - pj .
Аx
d 2p ^ & Pi+lj -Pij - Pij - Pi - lj ).
Аx
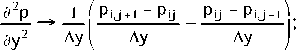
nk+1 nk
dp . p j- p j
![]()
Аx
at Аг
Подставляя (II. 154) в уравнение (II. 153), получаем
+ 1,j Ax
Ax
Ax
АУ
АУ
1 & Pi+1, j - Pij Pij - Pi - 1,j к 1 & Pi, j+1 - Pij Pij - Pi, j -1 '
Ay
Pk+1 - Pk Pj P^ At
Здесь Pjj - давление в ячейке А в момент времени t;
Pij1
давление в той же ячейке в момент времени t + At.
Граничные и начальные условия при решении задач численными методами также приводят к соответствующей конечно-разностной форме. Соотношение (II. 155) представляет собой алгебраическое уравнение. Таким образом, при использовании конечно-разностных методов вместо дифференциальных решают алгебраические уравнения.
АНАЛОГОВЫЕ МЕТОДЫ
Рассмотрим в несколько увеличенном виде ячейку А (см. рис. 49). В соответствии с электрогидродинамической аналогией (ЭГДА) фильтрационные сопротивления можно заменить электрическими, как это показано на рис. 50. Согласно
закону Ома, для силы тока ix и i выражения
i _ ^ AU • j _ ^ AU
Х р Ax У Р Ay
где S - площадь поперечного сечения электрического проводника; р - удельное электрическое сопротивление; AU - приращение электрического напряжения.
Сравним выражения (II. 156) с формулой закона Дарси, представленной в конечно-разностной форме. Имеем
k Ap k Ap , ч
vx---- ; vy----. (II. 157)
П Ax ц Ay
в направлениях х и у имеем (II.156)
1
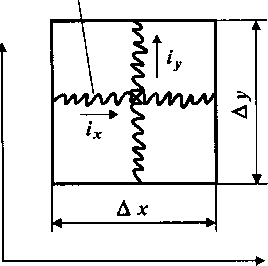
О х
Выражения (II. 156) и (II. 157) совпадают, если давление жидкости заменить электрическим напряжением, скорости фильтрации - силой электрического тока, а k/ц - величиной S/р. Указанные взаимно заменяемые величины - аналоги друг друга. Так, сила тока - аналог скорости фильтрации, электрическое напряжение S/р - аналог давления, электрическая проводимость k/ц - аналог фильтрационной проводимости.
В случае упругого режима аналогом сжимаемости пласта в является электрическая емкость С. Следовательно, можно написать
(II.158)
где a, b и с - коэффициенты пропорциональности.
Подставляя (II. 158) в уравнение упругого режима, получаем
(II.159)
bcS&д2U д2U' dU
![]()
Процессы, описываемые уравнением (II.159), можно моделировать на специальных устройствах, называемых электроинтеграторами, подключая к каждой ячейке соответствующие электрические сопротивления и электрические емкости. По формулам (II. 158) проводим пересчет электрических параметров, экспериментально определяемых на электроинтеграторах, на соответствующие фильтрационные параметры.
§ 12. МОДЕЛЬ ПЛАСТА С МОДИФИЦИРОВАННЫМИ ОТНОСИТЕЛЬНЫМИ ПРОНИЦАЕМОСТЯМИ
Относительные проницаемости - важнейшие
характеристики, определяющие внутрипластовые потоки нефти, воды и газа, а следовательно, обводненность продукции, текущую и конечную нефтеотдачу пластов.
Исходные измерения относительных проницаемостей производят на лабораторных установках путем осуществления фильтрации соответствующих флюидов через образцы пород пласта. Однако эти измерения относительных проницаемостей производятся на выбуренных из пласта образцах пород, имеющих, естественно, небольшие размеры. Так, диаметры и длины образцов цилиндрической формы составляют всего несколько сантиметров. При компьютерных расчетах разработки пластов приходится использовать конечно-разностные ячейки размером по площади пласта 20x20 м, 50x50 м, 100x100 м и более, в зависимости от размеров объекта разработки, требуемой точности расчетов и вычислительных возможностей компьютеров. При указанных выше размерах вычислительных ячеек потоки внутри них нефти, воды и газа будут значительно более сложными, чем потоки в образцах пород, изучаемых в лабораторных условиях, из-за значительно большей неоднородности пород, охватываемых конечно-разностной ячейкой. Также нельзя использовать неоднородность породы в ее образце-керне при расчетах разработки реальных пластов. Так, например, если площадь разрабатываемого объекта составляет 50 км2 (5x10 км или 5-107 м2), а толщина 10 м, то его объем составит 5-108 м3 или 5-1014 см3. При объеме вычислительной ячейки, равном 5 см3, понадобится 1014 ячеек, что является совершенно нереальным для осуществления расчетов разработки объекта.
Выходом из описанной выше трудности является использование модифицированных относительных проницаемостей, в которых учитываются как лабораторные относительные проницаемости, так и неоднородность пласта в пределах конечно-разностной ячейки. В зарубежной нефтегазовой литературе модифицированные относительные проницаемости получили название “псевдопроницаемостей”. В принципе известны два пути определения этих проницаемостей. Один из них состоит в их математическом моделировании с учетом лабораторных измерений и количественной интерпретации неоднородности пласта.
Второй путь заключается в получении модифицированных относительных проницаемостей на основе решения обратных задач разработки объекта. В этом случае осуществляется расчет разработки реального объекта при нескольких видах относительных проницаемостей. За истинные принимаются те из них, при которых расчетные данные лучше всего соответствуют фактическим. Естественно, осуществление второго пути возможно, когда имеется достаточное количество данных о разработке рассматриваемого объекта. Второй путь определения модифицированных проницаемостей равнозначен решению так называемой проблемы “идентификации пласта” или компьютерному воспроизведению разработки пласта.
В § 12 более подробно рассмотрен только первый путь получения модифицированных относительных проницаемостей.
Современные вычислительные возможности позволяют учитывать при расчетах разработки пласта многочисленные виды его неоднородности. К ним относятся крупномасштабные неоднородности, прослеживающиеся от ячейки к ячейке в достаточно больших объемах пласта. Вместе с тем среднемасштабную неоднородность с характерными размерами, например в несколько метров, очень трудно определить при больших расстояниях между скважинами, исчисляемых сотнями метров. Поэтому слои пласта, залегающие между крупномасштабными неоднородностями, считают условно-однородными. Конечно, эти условнооднородные слои являются неоднородными по сравнению с образцами пород, на которых получаются относительные проницаемости.
Количественное представление о среднемасштабной неоднородности дает детальное изучение данных геофизических исследований скважин (через 1 м и менее). Однако это делает возможным представить распределение слоев пород пласта-коллектора только по вертикали.
Распространение этих слоев по горизонтали определять затруднительно, хотя и возможно. Одним из способов преодоления этой последней трудности является компьютерный расчет модифицированных относительных проницаемостей при различных предположениях о горизонтальном распространении слоев, относящихся к среднемасштабной неоднородности, с последующим осреднением рассчитанных модифицированных относительных проницаемостей.
Процедура расчета модифицированных относительных проницаемостей в вычислительной ячейке, используемой для расчета разработки всего месторождения, состоит в следующем.
1. В вертикальном разрезе продуктивного пласта выделяются слои, обладающие среднемасштабной неоднородностью, т.е. которые можно считать условно-однородными. Например, на рис. 51 такими слоями являются слои 1, 3, 5, прослои 2 и 4 обладают такими значениями пористости, проницаемости и нефтенасыщенности, что их можно считать непроницаемыми, а нефть, которая может содержаться в них, - неизвлекаемой.
На основе детального изучения данных геофизических исследований скважин строится номограмма проницаемости по типу зависимости, данной в гл. 4 § 19.
2. Обоснованно выбирают значение (см. рис. 51) 6Ai в вычислительной ячейке Ax и считают, что в каждом вертикальном столбце микроячейки 6Ai реализуется набор проницаемых слоев, соответствующих общей гистограмме проницаемости для объекта разработки.
3. Осуществляют компьютерный расчет вытеснения нефти из ячейки длиной Ai.
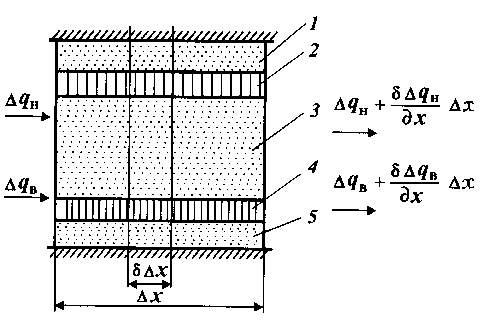
Рис. 51. Схема геолого-физического строения пласта в пределах вычислительной ячейки длиной АI:
1-5 - прослои различной проницаемости
4. Модифицированные проницаемости для нефти k(s) и воды k,(s), зависящие от модифицированной водонасыщенности s , определяют по формулам
Ms) = кнф / ко = AqH/Aq; K(s) = к„ф/к = АЯВ/АЯ-
где Aq - расход закачиваемой в вычислительную ячейку (“макроячейку”) жидкости; Aq = Aqн + AqB; кнф, кВф - физические относительные проницаемости, получаемые в результате лабораторных изменений; к0 - абсолютная проницаемость.
5. Модифицированная водонасыщенность s определяется следующим образом:
СВ 1 / м ’
где
^в ^вход ^выход ’
_ t
0
_t
Модифицированные относительные проницаемости можно определять не только для части разреза пласта, считаемой условно-однородной, но и для всего вертикального разреза пласта.
Если модифицированные относительные проницаемости определены только для условно-однородной части пласта, то при расчетах его разработки необходимо учитывать, что пласт разделен непроницаемыми прослоями типа 2 и 4 (см. рис. 51).
1. Расскажите о классификации моделей пластов.
2. Получите формулу, определяющую трещинную проницаемость трещиноватого пласта. Найдите связь между трещинной проницаемостью, густотой трещин и трещинной пористостью.
3. Объясните методику построения адресной модели пласта по данным геолого-геофизических исследований.
4. Напишите и объясните формулы плотности и закона логарифмически нормального распределения абсолютной проницаемости.
5. Напишите и объясните формулы плотности и закона гамма-распределения абсолютной проницаемости.
6. Какие фундаментальные законы естествознания используют при моделировании процессов разработки нефтяных и газовых месторождений? В виде каких уравнений они выражаются?
7. Что называется коэффициентом распределения (“константой равновесия”) вещества в газовой и жидкой фазах?
8. Напишите формулу, выражающую зависимость пористости пород пласта от среднего нормального напряжения. В какой теории используют эту зависимость?
9. Расскажите о связи между вертикальной компонентой напряжения (вертикальным горным давлением), средним нормальным напряжением и пластовым давлением. В какой теории используют эту связь?
10. Выведите формулу для распределения пластового давления в случае притока жидкости из однородного бесконечного пласта к точечному стоку. Покажите, какой вид приобретает формула при малых значениях. При каких расчетах используют эту формулу?
11. Выведите формулу для дебита скважины в элементе однорядной системы разработки методом эквивалентных фильтрационных сопротивлений.
2.1. ХАРАКТЕРИСТИКА РАЗЛИЧНЫХ РАСТВОРОВ ПРИ РЕМОНТЕ СКВАЖИН
При ремонте скважин используются рабочие жидкости различного назначения: для глушения, промывки скважин, гидроразрыва, химической обработки пласта и других работ.
В зависимости от степени дисперсности растворенного вещества растворы классифицируют на истинные, коллоидные, суспензии, эмульсии, коллоидно-суспензионные и др.
В истинных растворах частицы растворенного вещества состоят из отдельных молекул. Такие растворы прозрачны и, находясь в закрытом сосуде, могут существовать без изменения свойств долгое время. К ним относятся растворы неорганических солей, кислот и щелочей в воде.
На промыслах применяют водный раствор хлористого кальция, плотность которого может быть до 1400 кг/м3. Раствор хлористого кальция благодаря хорошей растворимости не образует осадка, не засоряет фильтровую зону. С увеличением концентрации раствора увеличивается температура замерзания. Так, 30 %-ный раствор CaCl2 с плотностью 1282 кг/м3 замерзает при температуре —50 °С.
Фильтрат технический пентаэритрита (ФТП) — жид
кость от бурого до коричневого цвета с осадком в виде тонкой взвеси со слабым запахом жженого сахара. Раствор находится в слабощелочной среде, т.е. рН = 7+9. Плотность жидкости до 1300 кг/м3. Раствор применяется в скважинах с забойной температурой до 100 °С. Вырабатывается Черкесским химическим заводом Ставропольского края и другими заводами.
Водный раствор бромида кальция (CaBr2) — тяжелая прозрачная жидкость плотностью до 1800 кг/м3. Преимуществом этих растворов считается легкость их приготовления, высокая регулируемая плотность и главное — минимальное повреждение пласта, так как высококонцентрированные растворы солей стабилизирующе действуют на глинистый материал коллектора, а отсутствие в этих растворах твердых частиц способствует сохранению проницаемости продуктивного пласта.
Выбор рецептур растворов на основе солей тяжелых металлов для ремонтных работ производится с учетом необходимости обеспечения стабильности раствора во времени, минимальной его стоимости, коррозионной активности и температуры кристаллизации, соответствующей предполагаемому температурному режиму использования.
В зависимости от необходимой плотности требуется различный компонентный состав солей (табл. 2.1).
Та б ли ц а 2 . 1
Плотность растворов солей в зависимости от компонентного состава
|
Соль | Диапазон плотностей раствора солей, кг/м3 | |
| KCl | 1000- |
-1160 |
| NaCl |
1000- | -1200 |
|
NaCl/CaCl2 | 1200- |
-1300 |
| ФТП |
1200- | -1300 |
|
CaCl2 | 1300- |
-1400 |
| CaCL/CaBr2 |
1400- | -1800 |
|
CaBr2/ZnBr2 | 1800- |
-2300 |
Для скважин, содержащих в пластовых водах большие количества карбоната и сульфат-ионов, рекомендуется использовать солевые растворы, не содержащие кальция, например, рассола бромида цинка с бромидами щелочных металлов. Плотность таких растворов может быть от 1380 до 2300 кг/м3.
Недостатками рассолов являются высокая стоимость используемых солей, коррозионная активность и высокая фильтрация.
В связи с последним фактором, во избежание кольмата-ции призабойной зоны пласта рекомендуется уделять большое внимание чистоте рассола, вплоть до применения фильтрующих элементов тонкой очистки, кроме того, необходима тщательная очистка емкостей, насосов и другого оборудования.
Для уменьшения фильтрации рассолов применяют органические полимеры-загустители, такие как лигносульфонаты, производные крахмала, производные целлюлозы, биополимеры. Наиболее эффективным загустителем концентрированных рассолов является оксиэтилцеллюлоза (ОЭЦ).
Исследования на искусственном керновом материале показали, что наибольшим эффектом по повышению естественной проницаемости кернового материала обладают солевые растворы на основе поташа (К2СО3) [21]. Плотность водного раствора К2СО3 может быть до 1500 кг/м3. В настоящее время только растворы на основе К2СО3 являются обрабатывающим материалом, способным не только восстановить, но и улучшить проницаемость глинистого песчаника.
Эта способность К2СО3 объясняется высокой активностью ионов калия и относительно невысоким (по сравнению с ионом хлора) гидратным числом иона СО3-2, поэтому при ио-нообмене с глинистыми минералами поташ обеспечивает уменьшение толщины гидратных оболочек на глинистых частицах и тем самым способствует повышению пористости и увеличению проницаемости заглинизированных песчаников. Введение в его состав комплексонов (НТФ, ОЭДФ) способствует дальнейшему уменьшению толщины гидратных оболочек и тем самым обеспечивает усиление указанного эффекта. В связи с этим технические жидкости на основе поташа с добавками комплексонов были подвергнуты полному комплексу исследований (В.М. Лимановский).
Исследования на коррозионную активность составов для глушения скважин и температура их замерзания показали целесообразность их использования в практике.
Результаты изучения данной проблемы приводят к следующим выводам.
1. В качестве жидкости глушения и перфорации, не снижающей проницаемость терригенных заглинизированных коллекторов, могут быть рекомендованы солевые составы без твердой фазы (не содержащие частицы размером более 2 мкм) на основе поташа с добавками комплексонов, так как они не только сохраняют, но и увеличивают естественную проницаемость кернового материала.
2. Солевые составы на основе поташа и комплексонов отличаются низкой коррозионной активностью.
3. Температура замерзания растворов поташа обеспечивает возможность круглогодичного использования их в качестве технологических жидкостей глушения.
У коллоидных растворов частицы состоят из многих молекул, и размер их может быть выражен долями микронов. Размеры частиц коллоидного раствора зависят от степени раздробленности, дисперсности вещества. Чем выше степень дисперсности, тем дольше может существовать коллоидный раствор без изменения своих свойств. Коллоидные растворы, как правило, мутные. При длительном хранении они теряют свои начальные свойства: растворенное вещество выпадает в осадок, или весь раствор образует студень. Примерами коллоидных растворов могут служить жидкое стекло Na2SiO3 и водный раствор КМЦ.
Суспензией называют дисперсную систему, состоящую из взвешенных в жидкости мелких твердых частиц. Например, мутная глинистая вода или же меловая суспензия в водном растворе КМЦ.
Меловая суспензия применяется при глушении скважин на время ремонта. Метод основан на способности суспензии в силу высокой дисперсности твердой фазы создавать в приствольной части пласта непроницаемый барьер, исключающий контактирование пород коллектора с рабочей жидкостью, находящейся в стволе скважины. При необходимости после окончания ремонта меловой барьер может быть разрушен соляно-кислотной обработкой, и гидродинамическая связь скважины с пластом восстановится.
Для стабильности меловых суспензий можно использовать КМЦ или ГИПАН. На основе промысловых данных рекомендуются следующие составы для временного блокирования пласта при глушении скважины:
мел химически осажденный плотностью 2,7+2,8 т/м3 — 35+40 %, мас;
вода пластовая — 58+63 %;
КМЦ-500 - 1,5+2,5 %.
При этом технологические параметры суспензии следующие: плотность — 1280 кг/м3; условная вязкость — 300 с; водоотдача — 20 см3/30 мин; суточный отстой — 0.
При взаимодействии соляной кислоты с химически осажденным мелом образуются водный раствор хлористого каль-
ция и углекислый газ, легко удаляемые из пор пласта в процессе освоения:
СаСО3 + 2HCl = CaCl2 + H2O + CO2.
Хлористый кальций хорошо растворим в воде, а выделяющийся углекислый газ создает дополнительную энергию, способствующую процессу освоения.
В процессе разработки газовых и газоконденсатных месторождений, особенно на поздней и заключительной стадиях, возникает необходимость в проведении ремонтных работ в скважине, дополнительном вскрытии продуктивного пласта, промывки призабойной зоны. Используемые при этом жидкости на водной основе с содержанием твердой фазы (преимущественно глины, нередко с утяжелителями) по причине кольматации призабойной зоны не обеспечивают должной эффективности, существенно затрудняя освоение скважин и дальнейшую их эксплуатацию. Значительно уменьшить или полностью исключить отрицательное влияние рабочих жидкостей можно, используя гидрофобно-эмульсионные растворы.
Гидрофобные эмульсии представляют собой полидисперс-ные системы, дисперсионной (внешней) средой которых является углеводородная жидкость с растворенным в ней эмульгатором, а дисперсной фазой (внутренней) — вода или водные растворы солей, кислот, щелочей. От химической природы эмульгатора зависит тип эмульсии, ее структурно-механические свойства и стабильность.
Эмульгатор-стабилизатор — это поверхностно-активное вещество (ПАВ), способное снизить поверхностное натяжение на границе раздела фаз углеводородная жидкость — водная фаза таким образом, что при их интенсивном перемешивании происходит образование мелких капелек водной фазы в углеводородной среде. При определенной концентрации эмульгатора они оказываются сплошь покрытыми участками молекул ПАВ, ввиду чего создается механически прочная оболочка вокруг капелек (структурно-механический барьер), которая препятствует их коалесценции (слиянию).
Химической промышленностью выпускается много эмульгаторов. Но их стабилизирующая способность различная, и образуемые с их применением эмульсии по своим свойствам не всегда соответствуют требованиям, необходимым для проведения работ в конкретных пластовых условиях. Например, известна гидрофобная эмульсия для обработки пласта состава, % (объем): нефтепродукт 34+62, минерализованная вода (в частности, раствор хлорида кальция плотностью 1300 кг/м3) 35+65, дегидратированные полиамиды 0,5+1,5, битумный структурообразователь 0,5+1,5. Плотность эмульсии 900+1000 кг/м3 [19]. Недостатками данной эмульсии являются большое содержание нефтепродуктов, сложный состав, что ограничивает возможность регулировать ее свойства.
Получать гидрофобно-эмульсионные растворы с регулируемыми в широком диапазоне реологическими свойствами и плотностью без твердой фазы стало возможным благодаря новым эмульгаторам-стабилизаторам ДЭСКА-17-20 и РЭМ, разработанным совместно сотрудниками Кубаньгазпром и СевКавНИПИгаза.
Гидрофобные эмульсии с эмульгатором ДЭСКА-17-20 [5] прошли опытно-промышленные испытания при гидроразрыве пласта на Николаевском, Челбасском и других месторождениях, показавшие высокую технологичность и техникоэкономическую эффективность [8].
Более широкое применение в качестве рабочих жидкостей при выполнении различных работ в скважинах находят гидрофобно-эмульсионные растворы с эмульгатором под фирменным названием РЭМ.
Эмульгатор РЭМ, вырабатываемый по ТУ 10-191-032-01 — 90, является катионоактивным ПАВ сложного состава, что позволяет в отличие от других эмульгаторов получать гидрофобные эмульсии с большим содержанием в них растворов различных неорганических солей и соляной кислоты. Хорошо растворяется в подогретой до 30+35 °С углеводородной жидкости, недостаточно быстро и полно при обычной и отрицательной температурах. Экологически безвреден, нетоксичен. Высокая эмульгирующая активность и стабилизирующая способность его позволяют получать концентрированные нейтральные эмульсии с малым, 15+20 %-ным (объемные доли) содержанием в них углеводородной жидкости, с большим, 80+85 %-ным содержанием водной фазы и 0,3+0,7 % эмульгатора.
В качестве дисперсной фазы могут использоваться вода техническая, пластовая, растворы неорганических солей любой плотности — хлоридов натрия, кальция [7], аммонизированного раствора нитрата кальция [8], а также растворов соляной кислоты [9].
В зависимости от объемного соотношения жидких компонентов, их качества и плотности, количественного содержания в полидисперсной системе эмульгатора можно получить гидрофобно-эмульсионные растворы с большим диапазоном реологических свойств: вязкостью от 60 с до "нетекучей", стабильностью при нормальной температуре более 30 сут, при 97 °С более 4 сут, устойчивостью к твердой фазе во времени, необходимом для выполнения работ в скважине. Это выгодно отличает их от других жидкостей и обусловливает возможность широкого применения в различных технологических процессах нефтегазодобычи.
Эмульсии с вязкостью 90+200 с используются для глушения, промывки скважин и вторичного вскрытия продуктивного пласта. Эмульсии с вязкостью до 200+250 с обеспечивают выполнение процесса гидроразрыва пласта с высокими технологическими показателями и качественным закреплением кварцевым песком трещин.
Эмульсии с вязкостью от 300 с до "нетекучей" характеризуются малой подвижностью, продолжительной устойчивостью в пластовых условиях и используются наряду с выполнением других работ как агент, временно изолирующий продуктивный пласт.
О степени влияния различных жидкостей на устойчивость пород продуктивного пласта и фильтрационную характеристику призабойной зоны можно сделать выводы по результатам специально проведенных по методике МГУ [24] исследований на размокаемость пород, которая характеризуется потерей их механической прочности, скоростью и характером распада на отдельные кусочки после погружения в жидкость.
Под воздействием технической воды, растворов хлоридов натрия, кальция образцы пород, отобранные из основных продуктивных пластов месторождений Северного Кавказа, разрушаются полностью за время от 2 до 12 ч [24]. В гидрофобно-эмульсионных растворах разрушения таких образцов не наблюдается. Этим объясняется отсутствие пробкообразо-вания при использовании эмульсий, сохранение фильтрационной характеристики призабойной зоны. Кроме того, гид-рофобизирующие свойства внешней фазы эмульсии способствуют очищению ее от кольматантов при освоении скважины.
В табл. 2.2 приводятся некоторые составы эмульсий и их свойства, ориентирующие исполнителя в подборе рецептуры при проведении работ в скважине.
Составы и основные свойства гидрофобных эмульсий с эмульгатором РЭМ
| Состав, % (объемн.) | Плот ность, кг/м3 |
Вязкость условия, с |
Примечания |
|
РЭМ-0,3 Вода техническая плотностью 1000 кг/м3 — 80 Конденсат газовый — 20 | 950 | 90 + 120 | Устойчива до 90°С |
| РЭМ-0,3 Вода пластовая плотностью 1004 кг/м3 — 80 Конденсат газовый — 20 | 952 |
152+200 | То же |
|
РЭМ-0,4 Вода пластовая плотностью 1012 кг/м3 — 80 Конденсат газовый — 20 | 960 | 230 + 260 |
То же |
| РЭМ-0,4 Раствор хлорида натрия плотностью 1071 кг/м3 — 80 Конденсат газовый — 20 |
1004 | 250 | |
| РЭМ-0,3 Раствор хлорида кальция плотностью 1066 кг/м3 — 80 Конденсат газовый — 20 | 1005 | 265 | |
|
РЭМ-0,5 Раствор хлорида кальция плотностью 1066 кг/м3 — 80 Конденсат газовый — 20 | 1007 |
600 | |
| РЭМ-0,4 Раствор хлорида кальция плотностью 1200 кг/м3 — 80 Конденсат газовый — 20 |
1120 | 350 |
Устойчива до 100+120°С |
|
РЭМ-0,5 Раствор хлорида кальция плотностью 1400 кг/м3 — 80 Конденсат газовый — 20 | 1270 |
530 | Работоспособен до 140 °С |
| РЭМ-0,7-80 Аммонизированный раствор хлорида кальция плотностью 1340 кг/м3 — 80 Конденсат газовый — 20 | 1220 | 350 | То же |
| РЭМ-0,7 Аммонизированный раствор, утяжеленный хлоридом кальция до плотности 1573 кг/м3, — 85 Конденсат газовый — 15 | 1450 |
360 |
Качественные гидрофобные эмульсии с необходимыми реологическими свойствами можно получить только при точном соблюдении их рецептуры и технологии приготовления всех компонентов, порядка ввода в смесительную камеру (емкость) и гидравлического режима перемешивания.
После доставки на скважину всех материалов (углеводородной жидкости, воды, соли, эмульгатора) и подготовки из них жидких компонентов необходимо провести пробное приготовление насосными агрегатами эмульсии в объеме 1,5+2 м3 для уточнения режима их работы при обработке скважины.
Приготавливать эмульсию в зависимости от необходимости ее объема и оснащенности предприятия насосными агрегатами можно двумя способами. При первом, когда требуется небольшой объем эмульсии (15+25 м3), после подготовки жидких компонентов их хорошо перемешивают в одной емкости, затем работающим "на себя" через 10+12-мм штуцер насосом интенсивно прокачивают смесь до получения молочнобелой массы с нужной вязкостью.
При втором способе, когда требуется большой объем рабочей жидкости, ее приготовление заключается в последовательном выполнении следующих операций:
растворяют в 1/3+1/4 части расчетного объема углеводородной жидкости все необходимое количество эмульгатора РЭМ, затем этот концентрированный раствор тщательно перемешивают в остальном (2/3+3/4 части) объеме углеводородной жидкости;
в других емкостях готовят водную фазу с нужной плотностью;
обвязывают насосные агрегаты (их приемные шланги) с указанными емкостями, а нагнетательные трубы через смесительное штуцерное устройство с устьем скважины или с ос-реднительной емкостью;
в смесительное устройство, состоящее из камеры и трех штуцеров, с равномерной производительностью одним насосом подают через штуцер диаметром 6+8 мм раствор эмульгатора; через второй штуцер диаметром 10+12 мм двумя-тре-мя насосами с большей в 3 — 4 раза производительностью закачивают воду, при этом темп закачки каждой жидкости должен быть пропорционален их соотношению по рецептуре (15+20):(80+85); при встречном потоке жидкостей в смесительной камере устройства происходит качественное их перемешивание, диспергирование и при достаточно большой гидравлической мощности (давление на насосах 8+10 МПа) — 22 образование эмульсии при прохождении смеси через третий штуцер диаметром 14+15 мм; в случае несоответствия реологических свойств получаемой эмульсии заданным техническим планом на проведение работ ее следует интенсивно перемешивать в осреднительной емкости работающим "на себя" насосом через штуцер диаметром 14+15 мм.
Высокая технологичность гидрофобных эмульсий и эффективность их применения, наличие в достаточном количестве эмульгатора и местных жидких компонентов, простота приготовления имеющимися у предприятий техническими средствами способствуют широкому применению их в качестве рабочих жидкостей различного назначения в капитальном ремонте скважин. За последние 3 года с их использованием проведены работы более чем в 100 скважинах глубиной от 600 до 3400 м на месторождениях П Кубаньгазпром.
Глинистый раствор — это коллоидно-суспензионная система, которую готовят из глины и воды с последующей обработкой химическими реагентами. Бентонитовая натриевая глина является лучшим материалом для приготовления глинистого раствора.
Основной характеристикой глины является ее коллоидальность, которая определяет выход раствора из 1 т глины. Из табл. 2.3 видно, что чем выше коллоидальность, тем меньше расход глины. Количество глины (бентонитовой), расходуемой на приготовление 1 м3 раствора заданной плотности, определяют по формуле
о = рг(рг р -Рв), (2.1)
р г — р В
где рг — плотность глины (рг = 2,2+2,7 т/м3); рв — плотность воды; ргр — плотность глинистого раствора.
Та б л и ц а 2.3
Классификация глин по коллоидальности
| Плотность раствора, кг/м3, при 25 °С | Коллоидальность глины | Выход раствора из 1 т глины |
| До 1600 1060+1150 1150+1200 | Высококоллоидальная Коллоидальная Малоколлоидальная | 16 м3 и более 10+4 м3 3+1,6 м3 |
Допустим, что необходимо приготовить 40 м3 глинистого раствора плотностью р = 1,16 т/м3. Определить количество бентонитовой глины и воды.
Подставляя исходные данные в формулу (2.1), получаем
о = woa-i) = 0,26 т/м3.
2,6 - 1
Объем глины в 1 м3 раствора составит
т j 0,26 ^ л 3
V = —— = 0,1 м3.
г 2, 6
Объем воды будет равен V, = 1 — Vr = 1 — 0,1 = = 0,9 м3.
Для приготовления 40 м3 глинистого раствора плотностью 1,16 т/м3 необходимо:
V/ = V.V = 40-0,1 = 4 м3;
V,' = V.V = 40-0,9 = 36 м3.
Количество глины, расходуемой на приготовление 1 м3 глинистого раствора заданной плотности, подсчитанной по формуле (2.1), приведено в табл. 2.4.
Т а б л и ц а 2.4
Расход глины (в т), необходимой для приготовления 1 м3 глинистого раствора заданной плотности
| Заданная плотность глинистого раствора, т/м3 | Плотность |
глины, т/м3 | ||||
|
2,2 | 2,3 | 2,4 |
2,5 | 2,6 | 2,7 | |
| 1,08 | 0,094 |
0,091 | 0,088 | 0,085 | 0,083 | 0,081 |
| 1,10 | 0,131 | 0,127 | 0,122 | 0,119 |
0,116 | 0,113 |
|
1,12 | 0,169 | 0,163 |
0,158 | 0,153 | 0,149 | 0,146 |
| 1,14 |
0,206 | 0,199 | 0,193 | 0,187 | 0,182 |
0,178 |
| 1,16 |
0,244 | 0,235 | 0,228 |
0,221 | 0,215 |
0,210 |
| 1,18 |
0,282 | 0,272 | 0,263 |
0,255 | 0,248 |
0,243 |
| 1,20 |
0,319 | 0,308 | 0,298 |
0,289 | 0,281 |
0,275 |
| 1,22 |
0,357 | 0,344 | 0,333 |
0,323 | 0,314 |
0,307 |
| 1,24 |
0,394 | 0,380 | 0,368 |
0,357 | 0,347 |
0,339 |
2.7. ИНГИБИРОВАННЫЙ ГЛИНИСТЫЙ РАСТВОР
При работе в открытом стволе, где опасность прихвата велика, рекомендуется применять ингибированный глинистый раствор, характеризующийся низкими фильтрационными свойствами, высокой стабильностью и низким коэффициентом трения глинистой корки [18]. В буровой раствор, содержащий полимерный реагент, глинопорошок и воду, дополнительно вводят смесь нафтената алюминия с нефтью (НАН) при соотношении 1 : 25, неионогенное поверхностно-активное вещество (ОП-10), буровый уголь и утяжелитель при следующем соотношении компонентов, мас. %:
Вода................................................................................................. Остальное
В условиях буровой нафтенат алюминия готовят следующим образом. В глиномешалку объемом 4 м3 набирают 2,5 м3 воды и загружают 260 кг алюмокалиевых квасцов (17 ведер). Перемешивают до растворения. В полученный 10 %-ный водный раствор вводят 1300 л мылонафта, разбавленного водой
1 : 1, и перемешивают в течение 5 мин. Этого времени достаточно, чтобы в верхней части мешалки образовалось алюминиевое мыло. Через нижний кран (люк) мешалки сливают воду, а образовавшееся мыло растворяют в нефти 2,7 м3. Полученный нафтенат алюминия (НАН) вводят в глинистый раствор, стабилизированный ГИПАНом.
Надо отметить, что мыло поливалентного металла высшей жирной или нафтеновой кислоты, входящее в состав НАН, химически адсорбируясь на наиболее активной составляющей — глинистой фазе бурового раствора, придает ему ди-фильные свойства. При бурении дифильные глинистые частицы, а также свободный нафтенат алюминия, сорбируясь гидрофильной частью на выбуренной породе и стенках скважины, создают за счет своей гидрофобной составляющей барьер, препятствующий контактированию их с дисперсионной средой бурового раствора. За счет этого предотвращается набухание глинистых пород и резко сокращается наработка излишних объемов.
Неионогенное ПАВ, например ОП-10, при таком отношении его с НАН в области рН 8+9 избирательно сорбируется на поверхности кристаллических негидратированных частиц, например барита, увеличивая гидрофильность последнего и предупреждая прилипание друг к другу твердых поверхностей (флокуляцию). ПАВ помогают равномерному распределению всех компонентов бурового раствора, в результате чего повышается его структура, исключается седиментация утяжелителя. В предлагаемом растворе за счет неионогенного ПАВ, взятого в определенных соотношениях с НАН, утяжелитель барит не гидрофобизируется, и буровой раствор прекрасно утяжеляется. Для поддержания рН в пределах 8+9 в раствор может вводиться бурый уголь. Плотность раствора может быть от 950 до 2000 кг/м3.
Глинистые растворы, применяемые в бурении, предназначаются для выноса выбуренной породы с забоя скважины на поверхность; глинизации стенок скважины; создания противодавления на пласт, предотвращающего поступления в скважину флюида, а также обвал стенок; удержания выбуренной породы во взвешенном состоянии при прекращении циркуляции; охлаждения рабочей поверхности долота и инструмента; вращения вала турбобура при турбинном способе бурения.
При капитальном ремонте скважин требования к качеству глинистого раствора остаются теми же, что и при бурении. Плотность, условная вязкость, статическое напряжение сдвига, водоотдача, толщина фильтрационной корки, водородный показатель ионов рН — основные параметры, которые определяют в промысловых лабораториях и непосредственно на скважинах, где проводится капитальный ремонт.
2.8. ФИЗИЧЕСКИЕ ПАРАМЕТРЫ ГЛИНИСТОГО
Плотность (удельный вес) — масса (вес) единицы объема бурового раствора. Определяют прибором ареометром на скважине и пикнометром в лаборатории. Ареометр (рис. 2.1) состоит из стакана с раствором 2, поплавка-шкалы 1 и съемного груза 3. Стакан имеет внутреннюю полость, в которой заключена дробь, обеспечивающая необходимый вес стакана. Прибор имеет две шкалы, градуированные в г/см3: одна шкала имеет деления от 1,0 до 1,8; другая — от 1,7 до 2,5. Для измерения плотности с помощью ареометра необходимо иметь вертикальный сосуд, глубина которого должна быть достаточной для погружения всего прибора. Сосуд входит в ком-
Рис. 2.2. Пикнометр
плект прибора. Подготовка прибора к работе заключается в проверке его градуировки по воде. Для этого в стакан прибора заливают пресную чистую воду и присоединяют шкалу-поплавок. При этом необходимо следить за выдавливанием избытка жидкости из стакана. Если жидкость не выдавливается, то это означает, что стакан не заполнен. Правильно плотность может быть определена только при заполнении всего объема стакана. После этого ареометр опускают в сосуд с водой. По шкале ареометра читают результат определения плотности глинистого раствора. С закрепленным на стакане грузом может быть замерена плотность раствора не более 1,8 г/см3 (1800 кг/м3). Если раствор имеет более высокую плотность, то в этом случае груз снимают и определяют плотность по второй шкале.
Для определения плотности раствора пикнометром сначала в лаборатории определяют массу чистого и сухого пикнометра с погрешностью до 0,1 г. Затем определяют массу пикнометра с глинистым раствором с погрешностью до 1,0 г. Зная объем пикнометра, плотность раствора определяют по фор -муле
г У
где т1 — масса пустого пикнометра, г; т2 — масса пикнометра с раствором, г; У — объем пикнометра, см3.
На рис. 2.2 изображен пикнометр; он состоит из цилиндрического сосуда 2 и крышки 1, которая имеет сквозное отверстие для выхода раствора. Объем пикнометра 97 см3.
Условная вязкость
Вязкость глинистого раствора благодаря наличию в растворе твердой фазы — глины, образующей структуру, называют структурной. Структурная вязкость необходима для расчета гидравлических потерь. Структурная вязкость определяется ротационным или капиллярным вискозиметром и выражается в сантипуазах.
В промысловых условиях пользуются условной вязкостью, которая определяется прибором ВБР-1 или СПВ-5 (стандартно-полевой вискозиметр). Он представляет собой воронку с трубкой длиной 100 мм и внутренним диаметром 5 мм (рис. 2.3). В комплект входят также кружка и сетка для очистки раствора. Время истечения 500 см3 жидкости из налитых в вискозиметр 700 см3 через трубку диаметром 5 мм и есть условная вязкость. Выражается в секундах.
Водоотдача (фильтрация) — способность глинистого раствора отфильтровывать воду при повышенном перепаде давления.
За водоотдачу принимается количество фильтрата, которое отфильтровывается из раствора через фильтр диаметром
Рис. 2.3. Вискозиметр ВБР-1
Рис. 2.4. Прибор ВМ-6 для определения водоотдачи глинистого раствора
75 мм за 30 мин. Определяют прибором ВМ-6 (водоотдача по прибору Минензона), а также при помощи фильтропресса. Она выражается в см3/30 мин.
8 Q
Прибор ВМ-6 (рис. 2.4) состоит из 3-х узлов: основания 7, напорного цилиндра 3 и фильтрационного стакана 5 с принадлежностями. Фильтрационный стакан на верхнем конце имеет горловину с наружной резьбой и отверстием. Нижний конец имеет наружную резьбу М63 х 3. Обеззоленные фильтры 9 и прокладка 8, служащая для герметизации, расположены на основании 7. Узел напорного цилиндра состоит из собственно цилиндра 3 с ввернутой в него из алюминиевой прокладки втулкой, плунжера 1, притертого по втулке, и
груза-шкалы 2, укрепленного на плунжере. Шкала нанесена на прозрачную пластмассовую пластину и прикреплена к грузу винтами. Сквозь шкалу видна отсчетная риска на верхнем конце втулки цилиндра. В притертой паре втулка —плунжер—втулка возникает трение, влияющее на давление при фильтрации. Для устранения трения необходимо плунжер периодически вращать рукой. Для установки шкалы на "0" и спуска масла из цилиндра в нижней части его имеется отверстие, перекрываемое иглой 4. Масло из этого отверстия сливается в чашку. Нижний конец цилиндра 3 имеет внутреннюю резьбу для соединения с фильтрационным стаканом. Для уплотнения места соединения цилиндра со стаканом предусмотрена прокладка. Перед определением водоотдачи необходимо разобрать прибор: отвернуть цилиндр от стакана, вынуть пробку 6. Детали протереть насухо. Проверить, закрыта ли игла. Смочить один или два листочка фильтровальной бумаги водой и положить в основание. Заложить прокладку, ввернуть стакан в основание и вставить пробку. После этого тщательно перемешанный раствор налить в стакан прибора, навернуть на стакан цилиндр, налить в него машинное масло. Вставив плунжер и приоткрыв иглу, подвести нулевое деление на шкале к отсчетной риске на верхнем крае втулки цилиндра. В момент вытаскивания пробки пустить секундомер. После определения водоотдачи открыть спускную иглу, выпустить масло из цилиндра, вынуть плунжер, вылить масло и отдельно раствор. Промыть фильтрационный стакан водой, не разбирая его. Затем разобрать стакан, извлечь фильтр с глинистой коркой и замерить толщину корки.
Статическое напряжение сдвига (СНС)
СНС — сила, которую надо приложить к глинистому раствору, находящемуся в покое, чтобы вывести его из этого состояния. СНС определяют через 1 мин и через 10 мин покоя. Выражается в мг/см2. Так как глинистый раствор обладает тиксотропными свойствами, т.е. при покое способен загустевать, а при взбалтывании разжижаться, то коэффициент тик-сотропии (Ктикс) определяют путем деления численного значения СНС через 10 мин покоя на численное значение СНС через 1 мин покоя:
При качественной структуре глинистого раствора коэффициент тиксотропии равен 2^3. Например, замер СНС1/10 = = 3/6 мг/см2, следовательно, Ктикс = 6/3 = 2.
Содержание газа в буровом растворе
Определение содержания газовой фазы Г (%) основано на уменьшении объема бурового раствора под избыточным давлением 0,1 МПа. Для этого используют приборы ВГ-1 и ВГ-1М. При работе с прибором ВГ-1 собирают фильтрационный стакан прибора (рис. 2.5) и заполняют его доверху буровым раствором. На горловину стакана навинчивают цилиндр, заполняют его маслом и надевают плунжер с грузом-шкалой. Клапан, находящийся под решеткой фильтраци-
онного стакана, при измерении должен быть закрыт. Плунжер, сжимая пробу раствора с газом, опускается, и деление шкалы "газ", остановившееся против риски на верхнем крае втулки, укажет процентное содержание газа в объеме промывочной жидкости. При работе с прибором ВГ-1 объем газа в порции жидкости, налитой в стакан прибора, вычисляют по формуле
2AVr,
V.
где AVj, — отсчет по шкале прибора, см3.
Коэффициент сжимаемости промывочной жидкости
![]()
где V — исходный объем жидкости, налитой в стакан прибора ВГ-1. Коэффициент Ксж имеет большое значение для регулирования противодавления на пласт.
При отсутствии приборов рекомендуется использовать следующий экспресс-метод определения содержания газа в буровом растворе. В бутылку вместимостью 0,5 л наливают 250 см3 вспененного бурового раствора, плотность которого известна (р1). Добавляют достаточную массу пеногасителя и в течение 5 мин интенсивно встряхивают до полного исчезновения пузырьков газа. Замеряют плотность невспененного раствора (р2). Объемную долю газовой фазы (%) вычисляют по формуле
![]()
2.9. ХИМИЧЕСКИЕ ПАРАМЕТРЫ ГЛИНИСТОГО РАСТВОРА
1. Водородный показатель ионов pH — безразмерная величина, равная отрицательному десятичному логарифму концентрации ионов водорода в растворе: рН = —lg H.
При температуре 25 °С в нейтральной среде рН = 7, в кислых средах рН < 7, а в щелочных средах рН > 7.
—I-1-1-1-1-1-1-1-1-1-1-1-1-1-
Определяют рН глинистого раствора или его фильтрата прибором рН-метром или при помощи индикаторной бумаги.
Влияние концентрации водородных ионов на свойства глинистых растворов настолько значительно, что оно дает возможность по величине рН судить об их качестве. Так, между рН, стабильностью, вязкостью и тиксотропией глинистых растворов существует определенная зависимость. Увеличение концентрации водородных ионов в растворе способствует ускорению загустевания его, и тем самым повышается вязкость. Тиксотропия наиболее ярко проявляется при рН = = 8+10, т.е. в слабощелочной среде.
2. Определение гуматов натрия в фильтрате глинистого раствора. Этот параметр определяют в тех случаях, когда глинистый раствор стабилизирован углещелочным реагентом (УЩР). Для этого в промысловой лаборатории готовят реактивы: 0,2 н раствор соли Мора; 0,4 н раствор хромовой кислоты; дифениламиновый индикатор.
Для приготовления 0,2 н раствора соли Мора необходимо 80 г ее растворить в 1 л дисциллированной воды с добавлением 20 мл серной кислоты плотностью 1840 кг/м3. Для приготовления 0,4 н раствора хромовой кислоты необходимо 20 г ее растворить в 500 мл дисциллированной воды с последующим добавлением 500 мл серной кислоты плотностью 1840 кг/м3.
Дифениламиновый индикатор готовится растворением
0,5 г дифениламина в 100 мл серной кислоты плотностью 1840 кг/м3.
После приготовления реактивов в две колбы заливают по 5 мл разбавленного в десять раз темного фильтрата с добавлением по 10 мл хромовой кислоты. Кипячение ведут 5 мин, не допуская при этом бурного кипения. После охлаждения колбы добавляют по 250 мл дисциллированной воды и титруют солью Мора до светло-зеленой окраски. В качестве индикатора добавляют несколько капель дифениламина.
Содержание гуматов натрия определяют по формуле
% ГЫа = (n1 — n2)K,
где % rNa — содержание гуматов натрия, %; n1 — количество соли Мора на хромовую кислоту, мл; n2 — количество соли Мора на раствор, мл; K — постоянная величина, зависящая от соли Мора.
В полевых условиях качество фильтрата из глинистого раствора стабилизированного УЩР можно определить по цвету самого фильтрата — он должен быть черным. Если же цвет фильтрата светло-коричневый или он вообще обесцвечен, то глинистый раствор требуется обработать реагентами: кальцинированной содой с целью высадить ионы кальция, которые могли попасть при разбуривании цементного моста, а также другими реагентами, которые значительно устойчивее к солевой агрессии.
3. Содержание коллоидной фазы. Для определения коллоидной фазы необходимо приготовить посуду и химические реактивы: медицинский шприц, колбу коническую, бюретку, воронку стеклянную, электроплитку закрытого типа, 3 %-ный раствор перекиси водорода, 5 н раствор серной кислоты, дисциллированную воду, метиленовую синь и фильтровальную бумагу.
Для того чтобы приготовить 5 н раствор серной кислоты, необходимо 14 мл ее плотностью 1840 кг/м3 разбавить дисциллированной водой до 50 мл. Кислоту льют в воду, но не наоборот! Чтобы приготовить 3 %-ный раствор перекиси водорода, надо в 0,5-л мерную колбу налить 42,85 мл пергидро-ли и долить до метки дисциллированную воду. На 100 мл воды расходуется 8,6 мл пергидроли.
После приготовления химических реактивов надо отмерить шприцем 2 мл глинистого раствора и перенести в колбу. Добавить 15 мл 3 %-ного раствора перекиси водорода и 0,5 мл 5 н раствора серной кислоты. После тщательного перемешивания кипятить 4 мин с "обратным холодильником", т.е. в колбу вставить воронку. После охлаждения колбы замерить объем и добавить 35 мл дисциллированной воды. При помощи бюретки титровать метиленовой синью. Затем из колбы набрать каплю и нанести на фильтровальную бумагу. При недостаточном содержании для данной пробы метиленовой сини на бумаге от капли останется темный круг с резко очерченной границей.
Титрование надо вести до тех пор, пока не появится от капли на бумаге темным кругом голубой ореол. После этого через 2 мин надо взять пробу повторно — ореол исчезнуть не должен. Расчет ведут по формуле n = 0,96а, где n — процентное содержание фазы; а — количество метиленовой сини, мл; с — объем в объеме, равен 0,37а.
