Глава 4 продольные перемещения подземного трубопровода
ГЛАВА 4
ПРОДОЛЬНЫЕ ПЕРЕМЕЩЕНИЯ ПОДЗЕМНОГО ТРУБОПРОВОДА
Изменение температурного перепала и внутреннего давления в подзем ном трубопроводе вызывает в нем продольные напряжения. Величина эти напряжений зависит от перемещении трубопровода, которые в общем случае могут иметь место при изменении конструктивных параметров трчбо-провода. непрямолинейпости первоначальной осн, при переходе от подземной прокладки к открытой, прн разности величин воздействий (температурного перепада и внутреннего давления), при изменении геометрпче ских характеристик трубы (диаметра и толщины стенки) или при наличии упругих связей по концам трубопровода.
§ 1. Общее решение для определения перемещений и усилий при продольных перемещениях
Рассмотрим прямолинейный подземный участок трубопровода, правый конец которого неподвижен. Для общности решения будем считать, что трубопровод имеет ограниченную длину L.
За начальный параметр пршшмаем осевое усилие Л'0, остальные оба! значения показаны па рие. ] 4
В качестве расчетной модели трубопровода используем стержень (балку) трубчатого сечения, взаимодействующий со средой. Взаимодействие трубопровода с грунтом описывается зависимостью сопротивления грунта от перемещения, диаграмма приведена на рне 15, о Она учитывает ограниченность по величине реакций продольных связей Аналитическое выражение модели грунта, представленной на этой диаграмме, имеет вид:
tx -¦
—nDncxorix, при |
| -sg J"v ,
(4.1)
nDnCx о
tx
= t„p. при i tix 1 > ¦
*np—, '4.2)
я Dhcx „
Здесь tx — сопротивление грунта продольным перемещениям трубы; сх о — коэффициент пропорциональности, называемый обобщенным коэффициентом касательного сопротивления грунта.
В зависимости от нагрузок, воздействий н относительной жесткости тру-; бопровода возможно, что на всей длине рассматриваемого участка грунт работает только в упругой стадии, характеризуемой условием (4.1), либо
на этом отрезке имеют место два участка, описываемых условиями (4.1)
и (4.2).
Участок, где взаимодействие трубопровода с грунтом описывается зависимостью (4 2). назовем участком предельного равновесия, а его длину
обозначим через /„р, в дальнейшем будем называть его просто первым
участком.
Уравнение равновесия элемента dx (см. рис. 15,6) имеет вид
dNx!dx+ tx = О. (4.3)
С учетом (4.1) и (4.2) для каждого из участков это уравнение запишется так:
dh’i'dx 4- fnp = 0, при |%|>—-¦; (4 4)
о
No, L
?t,p
—г,„
d,V и dx ~ xDHcx о =- 0, при
tv, p
nDy\Cx о
»x I se'
tnp'
<;00i ношение тсрмоупругосги, учитывая двухосное напряженное состояние напорного трубопровода,
\( ст вид Рне. 14. Расчетная схема подземного
:Vx ,v jjgnu(46) >частка трубопровода
P' EF Е
Здесь е* — продольная деформация; Е —¦ модуль упругости материала; f — площадь сечения стенок трубы; а — коэффициент линейного расшнре нпя; St—температурный перепад, положительный при нагревании; р— ко эффицнент Пуассона, окц — кольцевые напряжения от внутреннего давления.
В линейной постановке задачи деформации и перемещения связаны зависимостью
Ex~dudx. (4.7)
Тогда
d'1 (a&tE — |xoKU) F. (4 8)
Nx~ EF -
dx
Используя (4.8) и считая, что сечение трубопровода, температурный перепад гг внутреннее давление будут постоянными по длине, уравнения равновесия (4.4) и (4 5) в перемещениях имеют вид.
-) v2"i( = 0, (4 10)
где
y* = nDHcxo'EF. (4 11)
Запишем решение уравнений (4.9) н (4.10) относительно перемещенмй
и усилий:
(4 12)
(4.13) (4 14)
(4.15)
«I =
Ni = - V+ci - (аА^ - и°кц)F "и ~ С3 5,1 Vх + С}] Y*'
Vjj =-- EFy (Cg ch у* - C4 sh y*) — (a.ME — цскц) F.
(JT
-dx-
Считаем, что параметры трубопровода таковы, что по длине трубопровода ямс-стся участок предельного равновесия грунта Тогда граничные условии н условия сопряжения обоих участков и данной постановке' задачи имеют вид:
при х •= О N
Лт = Л'п,
1Ь
о>
ПРИ x = ,iip м1 = “
и.. = — н„п - — t nDwcx 0; при ЛГ = L и„ = 0.
"пр *пр'*"'н‘'жо’ л " “II ^
Исходя из этих условий, определяем произвольные постоянные Ci—Ct I уравнений (4.12)—(4 15) и длину участка предельного равновесии
(4.17)
^|1Гк ^пп /
пр /
-CsthZ.
С. __ пр пр _
7flp(ch /пр — thi sh/np)
Величину tnj, определяют по трансцендентному уравнению, решая его относительно 1ВР-
I fh L fh р , — _-jj
--3-- ”Т ьнр —“ i* •
th t — th/пр
Здесь введены следующие безразмерные параметры
1 =¦ У1* \Р = v/Iip; Л' = т(^-Л^)%,
(4 18) (4.19)j
где
ЛГ<» = ( - -l f!crKU) F. (4.20)
Определив из уравнения (4.18) luv, по формулам (4 17) находим произвольные постоянные, которые позволяют с помощью уравнений (4.12)
(4.15) определить перемещение и продольное усилие любого сечения тру
бопровода.
Запишем значение продольного перемещения и продольного усилия соответственно в начале н конце участка трубопровода:
«о = Cs!EFi (4.21)
—V r (4.22) ’
A'l~ Л'с
chaL
Рассмотрим один из наиболее распространенных случаев, когда участок трубопровода можно считать полубесконечным, т. е. прн L-+-оо. Для получения необходимых расчетных формул раскроем неопределенности в (4.17) и (4 18). Из (4.18) находим
1 I ~
А » IПр —
1
(4.23)
^пр — Л' -
t
пр
Произвольные постоянные в этом случае записываются в виде
нр
С2 =
2<„РТг
Л' Л’
пр
Е Fy е
пр
„в ---LJ
<*Ь- + Js!L
] . (4
25)
> ли в «защемленной» части трубопровода, где перемещение равно нулю,
составит
A'l — Л'» - ( — аМЕ цока) F. (4.26)
Для опенки размера участка который можно принять за бесконечно
д. шшьгй, примем условие, что перемещение его правого конца равно 1 %
о перемещения, соответствующего перемещению конца участка предельного равновесия, т е.
iil — 0,01 «,,р -
0,01 ¦ ~~SE~
¦ (4 27)
Из (4 12) с учетом 4.27) получим уравнение дтя L
f. i (4,28)
V ^Пр
По этой формуле можно определять длину участка трубопровода, с ко ropoi о «собираются» перемещения к его началу.
Изложенное относится к случаю, когда по длине трубопровода имеются два участка: участок предельного равновесия грунта /и,„ где сопро тизпение но длине постоянно и равно /цр, и участок упругой работы грунта, где сопротивление грунта пропорционально перемещению. Критерий наличия уч стка предельного равновесия грунта можно получить из (4.18), считая, что /ni»>0. Тогда указанный критерий можно записать в виде
N thZ>I. (429>
Дтя полубесконечного участка этот критерий будет иметь вид
<*?-%>!_ > j. (4.30)
^пр
Теперь рассмотрим случай, когда участок предельного равновесии от-
сутствусг. т. е. когда критерии (4.29) и (4 30) не выполняются. Как и ра
нее рассматриваем в качестве начального параметра (при х=0) продольны усилие Л'0.
Уравнение, описывающее изменение продольных перемещений и продольных усилий по длине трубопровода, записывается аналогично (4.14). (4 13).
ux — sh ух -f- D,, ch уд\- (4.31)
Nx = EFy (D, ch yx D2 sh Vх) — (a&tE — Цокц) F. (4.32)
Произвольные постоянные D, и Z>2 определяем изграничных условий: при х= 0, Nx — Nn’> при х = L, их = 0 (4 33)
Продольное перемещение и продольное усилие соответственно в начале « конце участка трубопровода будет
Л'., - AL,
Для полубесконечного участка при L-xx, UvyL-И; chy L—+cx>. Для оценки длины участка, который можно принягь за полу бесконечный, используем тот же критерий. Тогда длина участка определится по формуле
L^-Li„. . (4 36).
У (No-N~)y
Полученные зависимости позволяют решить ряд практических задач» если известен начальный параметр усилие No.
§ 2. Экспериментальное определение распределения продольных перемещений по длине трубопровода
Для анализа различных расчетных моделей грунта при продольных перемещениях трубопровода и экспериментальной проверки расчетных зависимостей нами были проведены эксперименты на длинной плети трубопровода диаметром 529 мм.
Трубопровод длиной 91,7 м был уложен в грунт на глубину I м до верхней образующей трубы. По длине трубы через каждые 17,2—19,8 м были устроены шурфы для измерения перемещений трубы и продольных напряжений в металле. Одни конец подземного трубопровода был свободен, к другому его концу с помощью двух гидравлических домкратов прикладывалось продольное усилие.
На рис. 16 показана зависимость перемещения сечения от приложенного к этому сечению усилия. На том же рисунке показано предельное усилие, при котором имело место поступательное движение трубы.
Для анализа влияния замены нелинейной диаграммы т—и линеаризованной теоретические кривые построены по линейной модели (2=1, сх о~ = 1,9 11/см3) и с учетом нелинейности (г=0,218, с2~0,75 И/см3). Значения этих параметров получены нами па основании опытов иа моделях и соответствуют зависимостям т*=—сх 0их и т*=—сги:х.
Продольное перемещение подземного трубопровода при действии продольного усилия S определяется по формулам:
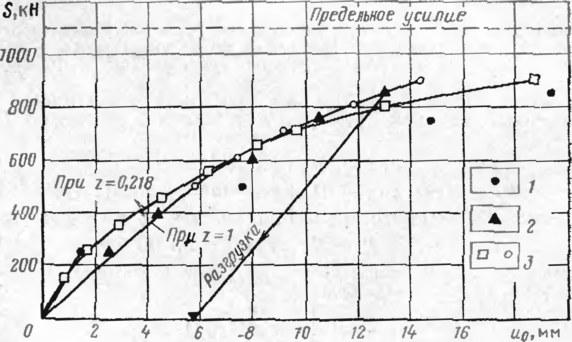
Рис 16. Диаграмма «продольное перемещение нулевого сечения — усилие»:
/ — первое нагружеиис; 2 — второе нагружение; 3 расчетные точки
ni) отсутствии участка предельного равновесия грунта, т. е.
(ipil tx<.tav
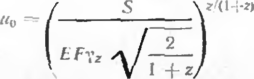
нрп наличии участка предельного равновесия грунта
(4.38)
![]()
![]()
__ <(2+1) 22 /р С><2—1) 22
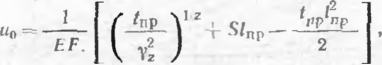
(4.39)
где —длина участка предельного равновесия грунта
(4.40)
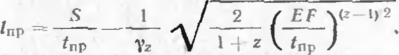
Графики зависимости продольного перемещения от продольного усилия п соответствии с формулами (4.32) и (4 33) при z= 1 и при г=0,218 приведены на рис. 16. Результаты эксперимента свидетельствуют о том что полученные уравнения достаточно хорошо описывают фактическую работу трубопровода. Перемещения по длине подземного трубопровода выражаются следующими уравнениями, полученными на основании решений дифференциальных уравнений равновесия трубопровода прп отсутствии участка предельного равновесия грунта
при наличии участка предельного равновесия
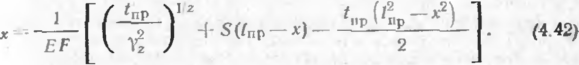
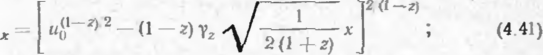
На рис. 17 в соответствии с уравнениями (4.41) и (4 42) построены кривые, характеризующие изменение перемещения по длине труби при различной продольном усилии S, а также приведены экспериментальные данные. Характер действительных продольных перемещений различных сече
1 ий по длине трубы достаточно хорошо согласуется с уравнениями (4.41) и (4 42). Фактические перемещения трубы по длине более точно описываются уравнением, учитывающим физическую нелинейность сопротивления грунта.
Таким образом, на основании сравнения экспериментальных данных ¦с расчетными можно сделать вывод, что учет упругопластической работы грунта с помощью обобщенного коэффициента касательного сопротивления позволяет с достаточной для практики точностью определить продольное перемещение подземного трубопровода ь месте его выхода на поверхность
— при ?=Ч\218,
§ 3. Определение перемещений в месте выхода подземного участка трубопровода на поверхность
• — при 2= I
Для ряда конструктивных решений, применяемых при надземной прокладке трубопроводов, пренебрегая влиянием несущественных факторов, можно получить решения в Замкнутом виде.
Для открытых участков, имеющих П-, Z". Г-образпые и другие компенсаторы, или надземных переходов арочного типа можно принять, что отпор этих конструкций пропорционален перемещению, а усилие от внутреннего давления равно произведению давления на площадь трубы в свету. Тогда начальный napavierp - продольное усилие Л'0 будет
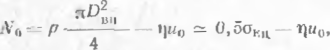
(4.43)
где I)—жесткость конструкции, т. с. усилие, вызывающее единичное перемещение ее конца.
При наличии полу бесконечного подземного участка из уравнении (4 25) к (-1S4) можно определить продольное перемещение в месте нрнмыкания его к открытой части трубопровода, дополнительный распор и длины подземных участков, на которых происходит перемещение:
а) при наличии участка предельного равновесия, т. е. при выполнении условия (4.44)
S'V
![]()
>1;
(4.44)
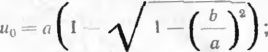
(4.45)
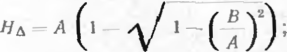
S , E Ftnr> .
a ~--1--•—" ’ iii
- iihm-
A — r]a; В2 = i]4»2. (4.50)
При ?/«<0,1, используя правило приближенных вычислений, можно считать, что
Если пренебречь жесткостью конструкции т), то, раскрывая неопрсделен-' иосгь в (4 45), можио получить
б) при отсутствии \частка предельного равновесия грунта, т. с. при невыполнении критерия (4.44), тс же величины определяются по формулам:
S
«о = —ГГ-г (4 54)
EFy
1-1-ч
Дтя различных тппов конструкций, примыкающих к подземным участкам, жесткость определяется методами строительной механики, например» методами сил или перемещений.
Для практических расчетов систем с компенсаторами их жесткость »ожно определять в соответствии с нормами СНиП 11-45—75 по формуле
Пк - ЕЧК (4.57)
Параметр й,. определяется по следующим формулам: для Г образного компенсатора
К ; (4.58)
для П образною компенсатора
2р2Л-».33,)3к; (4.59)
![]()
![]()
В формулах (4.58)—(4.60) приняты следующие обозначения:
k — коэффициент уменьшения жесткости отвода; р — радиус изгиба оси] 'отвода; /к — вылет компенсатора; In—ширина полки компенсатора.
Так как параметры открытых компенсаторов являются функцией их компенсирующей способности, то эти параметры подбираются методом последовательных приближений. Вначале принимают жесткость компенсатора] 1]„=0 и определяют продольные перемещения но формулам (4.53) или (4.54). Определив параметры компенсатора, исходя из компенсации вы-1 числепных продольных перемещений подземной и открытой частей трубопровода, находят его жесткость.
Далее, по
формулам (4 45) или (4.54) определяют уточненное
значе-1 ние перемещений, по которым пновь
уточняют параметры компенсатор «Обычно
двух приближений бывает достаточно, чтобы
определить расче![]() ные
параметры компенсатора. ¦
ные
параметры компенсатора. ¦
§ 4. Определение расстояний между компенсирующими устройствами
Как известно и подтверждается приведенным решением (4.26). про-1 дольное растягивающее усилие в стенках трубы в защемленной части тру-1 бопровода
N„ ( *\tC | ioKa)F. , (4 61)
При значительном положительном температурном перепаде продольное! осевое усилие может быть сжимающим (знак минус), что, учитывая двух-1 оспое напряженное состояние трубопровода, может привести к исчерпанию! предельного состояния. Кроме того, при этом существенно увели'
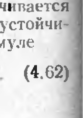
¦и эквивалентное оссвое сжимающее усилие, вызывающее потерю «ости подземного трубопровода. Это усилие определяется по фор»
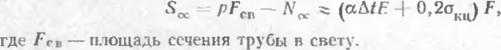
При наличии компенсаторов по длине трубопровода происходит умень-М шение продольного, усилия.
На оспованин решения (4 13) и (4 15), считая, что No 0,5а,;ЦГ (при ] наличии компенсатора), и пренебрегая отпором компенсатора, построим I эпюру продольных усилий по длине трубопровода (рис. 18).
За ось симметрии иа рис. 18 принимается середина между двумя со-1 седиим и компенсаторами, пунктиром показано распределение продольного j усилия при полубееконечном участке трубопровода. Обозначим допускае- 1 мое из условия прочности или устойчивости усилие иа расстоянии L от 1 компенсатора через [Л;] и определим искомое расстояние.
Приняв в формуле (4.22) или (4.35) Л'7, =[/V], из нелинейного уравис-¦ ния определим искомую величину L. Уравнение (4.22) или (4.35) можно 1 решить методом последовательных приближений с помощью простейшей I программы на ЭВМ, составленной по следующей блок-схеме. Задаемся дли-1 бой L, равной половине расстояния между компенсаторами, величину No, I пренебрегая отпором компенсатора, принимаем равной No=Q,5cr,.„F
По формулам (419) определяем безразмерные параметры L и А. ja- I лее, проверяем критерий (4.29). Здесь последующее решение разветвляется. | "Если условие (129) выполняется, то. решая нелинейное уравнение (4.18), . определяем длину участка предельного равновесия грунта /Пр, далее, по 1 формулам (4 17) определяем произвольные постоянные, затем по (4 22)—- J
ж
Эпюра N
Ш
-i-=*сщд
^ЩЩр31Е====-
Рис. 18. Эпюры продольных усилий и перемещений при подземной прокладке с компенсаторами
vcinHe в ссченни трубопровода :юсёрелнпе между комненсато-алн Если это усилие отличается 1; юпуекасмого [А'] более чем на 5 10 то, принимая повое значение расчет повторяют. Если
условие (4 29) не выполняется, то усилие определяется по формуле
(4 33). „
После итерации по формуле (4.21) или (4.34) вычисляют искомое перемещение, по которому н дбираются параметры компенсатора.
.Можно, несколько усложнив программу, весь расчет выполнить
па ЭВМ, учитывая при этом и жесткость компенсатора. В этом случае нужно дополнить программу вычислением параметров компенсатора и его жесткости. Определив жесткость компенсатора но перемещениям, находят его отпор, а следовательно, получают и более точно значение Л'о. В качестве критерия сходимости здесь можно принять условие близости двух значений Vo, определяемых в двух последующих этапах вычисления. Можно предложить приближенною методику определения расстояния между компенсаторами (в пашем случае определение 2L), основанную на ряде допущений. Даже при наличии программы расчета ка ЭВМ методика позволит задаваться значением I па первом приближении.
Вначале считаем, что грунт иа всем участке работает в упругой стадии, тогда из (4.35), принимая NL— [,V], определяем длину L. По критерию (4 29) проверяем справедливость нашей гипотезы. Если условие (4.29) не выполняется, то определенная по (4.35) длина является искомой Если же условие (4.29) выполняется, то иа рассматриваемой длине имеется участок предельного равновесия грунта. Тогда принимаем, что влиянием упругой работы грунта можно пренебречь, и искомая длина определится по формуле
[Л-1
(4.63)
‘пр
Величина продольного перемещения подземного участка трубопровода в месте примыкания к компенсатору определяется по формуле
0,2 о,
(¦
\t
(4.64)
ы„
<пр?а 2 EF
Отметим, что при определении расстояния между компенсаторами коэффициенты перегрузки для грунта следует принимать более единицы, а при определении перемещения — менее единицы. Это связано с необходимостью в обоих случаях вести расчеты в запас прочности.
§ 5. Определение продольного перемещения в месте сопряжения двух участков трубопровода с различными температурным перепадом и внутренним давлением
В местах расположения компрессорных станций со стороны входа и пыхода продукта давление и температура иа двух участках трубопровода могут быть различными (рис, 19, а). Кроме того, при строительстве лупин-
1 ‘>в, чтобы уменьшить перемещение в месте соединения его с основной пит трубопровода, вместо устройства упора укладывают некоторый уча--Тои трубы, который служит «якорем», уменьшающим перемещение (рис
КС
Atj,p/
Газ
тг
"*¦ l-я
Муг/инг A t,p
;At~V,p=0
Якорь
DcnoBnuf магистраль
Рис 19. Схемы участков с различными воздействиями
«<ч
(4 67)
Инг
19,6). Такой тип закрепления является более рациональным, чем устройство специального бетонного упора, так как трубопровод-якорь в дальнейшем используется в случае преобразования луни г, га по вторую магистраль.
В связи с этим возникает не' обходимость определения перемещения в месте стыка двух участ ков трубопровода, а при устрой' стве трубоировода-якоря — необ ходимость определения его мини малыюй длины, обеспечивающей минимальное перемещение.
Рассматриваем случай, когда фнзнко-механическнс характери стики грунта я геометрические] параметры тр^бы одинаковы для обоих участков, а длины участков таковы, что нх можно принимать нолубссконечнымв.
Решение будем искать как для статически неопределимой системы методом сил, используя ранее полученные решения для полу бесконечных участков
Разрежем рассматриваемый участок трубопровода в месте стыка, по j обоим концам установим заглушки и приложим к пим неизвестное усилие X. Его величину определим us условия неразрывности перемещений
м,ц -г- Wn2 (4.65)
где и«1 — перемещение сечения О, как свободного копия первого (левого) участка при воздействии температуры, давления и усилия Х\ «о»— то же, I для второго (правого) участка. Г
Как и ранее, рассматриваем два случая работы грунта на этих участках.
При отсутствии участка предельного равновесия грунта перемещения •определяются по формулам:
X— 0,2окц ,) F
FFy
X - -(a\i.2E + 0,2акп,) F EFy
Подставляя (4.66) и (4.67) в (4.60), получаем искомое усилие
(4 66)
о, 1 (окц X +
(4.68)
^кц F.
ТТодставляя (4 68) в (4 66) или (4.67), получаем искомое перемещение
Aft — М.2
(4.69)
ис = «
2Т
0,1 (окц t — °Kii. г)
су
Критерием отсутствия участка предельного равновесия является условие
unF.Fy*
(4.70)
пр
Выполнив вычисления по формуле (4.69), проверяют критерий (4 70). Если критерий выполняется, то полученное значение — искомое перемещение.
Ъяину участка, на которам происходит перемещение, определяют иэ н{,»р^ь'С11ПЯ (4.35), используя зависимости (4.68) и (4 69):
Если критерий (4 70) ие выполняется, то расчет необходимо выполнять по формулам, учитывающим наличие участка предельного раем овс-сия ]р\пта. Эти формулы получаем аналогично предыдущим, используя решение (4 25).
Неизвестное усилие X определяем по формуле (4.68), а продольное перемещение в месте стыка обоих участков и длина участков, на которых происходит перемещение трубопровода, определяютси соответственно по
формулам:
... - 1 [ ^»р , № S-i)'1 [.
1т* + 4^р ]’
(4 72)
2 F.F
*пр
•**i — ft ip
L - ~ f --- ---— — , (4 73)
7 ^np
где
S, =--- <aMJ: 0,2акц ,) F; S2 (aAf„? 0,2акц .J F. (4 74)
Причем >с.ювно принято, что Si>S0.
Пример 1. Определить продольное перемещение подземного участка сталь ного трубопровода в месте примыкания к открытому П-образному компеи сатору. Трубопровод диаметром DH = 1420 мм, толщиной стенки 6 - 19,5 мм; температурный перепад Л/=60 "С, внутреннее давление р 7,5 МПа, коэффициент перегрузки п,, = 1,1. Глубина заложения трубы (до верхней образующей) Л 100 см. Грунты-суглинки со следующими физико-механиче-сьимн характеристиками: объемный вес Y*p=0,0143 Н/см217, угол виутрен пего трения <|гР=-11°, удельное сцепление с,Р=0,01 МПа = 1 Н/см218, обобщенный коэффициент касательного сопротивления грунта сх о=0,026 МПа/см,
коэффициент перегрузки /гГр—ОД
Параметры П-образного компенсатора: вылет компенсатора 1К=20 м„ ширина полки компенсатора 1а~8 м, радиус изгиба оси отводов рк=280см Определяем жесткость компенсатора.
Параметр отводов:
Г2 ( 142 — 1,95 V
Коэффициент уменьшения жесткости отводов при /.<0,3 составляет
= —---0,067.
1,65 1,65
Изгибная жесткость прямой трубы будет
EI = -
64
Податливость П-образного компенсатора определяем с использованием! «формулы (4 59)
1
X
Е1 4,42-10»
X (1,42 2803-Ь 3,14 280-20001 — 2,28-280--2000) -0,67-200(Р —
— 1,34 280*-!- 2-2000-280s -f 800-2000-— 4 280 2000s} =
— 0,118 (МПа cm)-i = 0,118 10—а Н-1-см.
Жесткость компенсатора — величина, обратная податливости.
т|к — —=---— 8,5 МПа • см — 850 Н см.
6и 0,118
Определяем предельное сопротивление грунта продольным перемете киям трубы.
¦ _ ”1р2, °вн) _ я(1422 — 138.12)
Площадь сечения стенок трубы F
4 ’ 4
= 857 см2
•Бес единицы длины трубы цтр Y-n/ 7,85-10 2¦ 857 = 67,3 Н/см.
Вес продукта (газа) в единице длины трубы
Ягйз- 100прр?^н = 0,95-100 7,5-1,3812 — 1360 Н/М = 13,6 Н/см.
Вес трубы с продуктом
Qn. т ” Ятр ' Q газ ^>7, 3} 13,0 - В1 11 Ч\м.
Коэффициент, } читывающий образование свода естественного равновесия ¦ грунта, определяем по формуле (3.22)
сЛ — 0 046 (-Y 0,307 0,06 0,30.
V 142 J 142
Предельное сопротивление грунта сдвигу определяем по формуле (3.20)
tfnp = 0,8 (81 tg 11 + 2 0,0143 0,3л 1422 tg 11° 0,6я 142-1.0) =
311 Н/см 3,11 МПа-см.
Определяем эквивалентное продольное усилие.
Находим кольцевые напряжения ск
1,1.7,5 138,1
flppDs и
jku
26 2-1,95
= 292,1 МПа; эквивалентное усилие 6} дет
S (12-10~6-60-2,1 106 + 0,2-292,1)857= 1,797 10® МПа-см» =
= 1,797-107 Н.
Определяем параметр упругой работы грунта по формуле (4.11)
Vn 142-0,026 . -1
---= 2,54 10 см .
2,1 10» 857
Проверяем критерий, характеризующий наличие участка предельного равновесия груита по длине трубопровода, по выражению (4 44)
этом случае продольное перемещение определяют по формуле 14.45). По форм' l;,M "(4.49) определяем параметры а и b
1,797-1№ . 2,1 - Ю5-857-3, П
- — 7,77- 10е см.
8,5 8,52
( 1,797 № V ( 3,11 V2 , ,, 1ПЯ.
Ь~ I-1+1--I — 4,а1-109см-.
V 8,5 / 1,2,54-10-J-8,5 )
Ь V4.51 -108 ~= 2,12-104 см.
Так как Ь/а=2,12 • 104/7,76 • 10®=0,0027 <0,1, то для определения нереме-ения но формуле (4.45) используем приближенное выражение (4.51)
„0 , _L.
' !^1 29,03
см.
2 7,77-106
Дли i\ участка, на котором имеют место продольные перемещения, определяем по формуле (4.47).
3 t.797-10‘-0,85-109-29,03 .
L —------1 —---------- = о,7/ • 104 см 5/7 м.
2.54-Ю-» 219 311
Пример 2 Определить продольное перемещение в месте сопряжения двух участков газопровода е различным температурным перепадом и внутренним давлением. Для первого участка Л?,=С0 °С, р(=7,5 МПа; для второго участка 1(, -4о “С, ps=o МПа.
Трубопровод иа обоих участках из труб 1420X19,5 мм, грунтЫ'суглинки со следующими характеристиками: объемный вес груита \*гр*=1.43 • 10~2
Н/см3, угол внутреннего трения <frp= 11°, удельное сцепление сгр—0.01 МПа-1 Н/см2, обобщенный коэффициент касательного сопротивления грунта с-с а -0,026 МПа/ем, площадь сечения стенок трубы F 857см!, вес едини ы длины трубы чТр=С8 Н/см, вес трубопровода (с продуктом) на первом участке <?ц,_ т=81.6 П/см, пв втором — c/zn т= 77,1 Н/см.
Определяем кольцевые напряжения от расчетного внутреннего давления:
а) на первом участке
о1кц ---292,1 МПа;
ц 26 2-1,95
б) иа втором участке
о, кц = JHHeSL. _ , 194,8 МПа.
ц 26 2-1,95
Опп еделяем эквивалентное продольное сжимающее усилие по форму ю
а) на первом участке
Л', (0,2-292,1 + 12-l0-*-2,l J0»-60)857= 1,795-105 МПа-см* =
- 1,795-Ю? Н;
б) на втором участке
(0,2-194,8 12 10~« 2,1-№ 45)857 ),306-10* МПа-см* =
== 1,306 10» Н.
Вычисляем параметр упругой работы грунта по формуле (4 11)
Vjil42-0,026
2,1 105 857
Предельное сопротивление грунта продольным перемещениям трубы оире целяем по формуле (3.20)
а) на первом участке
<1пр 0,8(81,6tg 1Г-j-2-0,0143-0,32 3,14-142220 tg +
-f 0,6-3,14 142 l,0j= 316,8 Нем = 3,168 МПасм;
б) на втором участке tmv—316,1 Н/ем 3,61 МПа-см.
Определяем продольное перемещение газопровода в месте стыка двух!
участков в предположении отсутствия участка предельного равновесия грунта
5, — S, 1,795-10*— 1,306-105
Ло — —*-— =-----—- — 0,53 см.
2EFy 2 2,1-105-857-2,54 - 10-*
Проверяем критерий
Л„FFy* 0,53 2,1 105 857(2,54 10 *)* , ,
--—---— — 1,9/ > 1.
tup 3,168
Так как критерий не выполняется, то расчет ьедем с учетом наличия )ча стка предельного равновесия грунта.
Усилие в месте стыка участков трубопрогода определяем, решая уран пеиис
a№-~2hN с 0,
т де
1 1 1
Ftlip Ft2„ р = 857-316,8
1
— 0,117 10—- (Н ем)-»;
857 • 316,1
-S', S., 1,790-10? 1,306-10-
4=----=— -------;—— — 17,916 См~А
Ft, „р f/2Iip 857 • 316,8 857 - 316,1
А ир *2 пр ^2 _ 316,8
Ft ~~ Ft ~ Ftt up " Ftinp 857 (2,54-10^
316,1 (1,796 10')* (1,306- W7)s
| Г 3,168 |
(1,796-105 —1,551 Ю5)2] |
| |(2,54-10-4)* |
4 3,168 |
1,796-10' — 1,551- 107 —
316,8
на втором участке
2,54-10“221
--1о619 см 156 м;
3 , ' " 2,54-10-222
I, ------5- -I----156 М.
2,54-10 4 1 316,1
Таким образом, перемещение в месте стыка обоих участков составит 0,67 см, а длины участков, на которых происходит перемещение,— примерно 156 м.
Приведено решение, когда вследствие разности удельных весов трубопровода с продуктом изменяются предельные сопротивления грунта нро-дшыгым перемещением. Предельные сопротивления гвинта могут также изменяться за счет различных физико-механических характеристик грунта.
При одинаковых параметрах трубы и грунта иа обоих участках решение упрощается. Решим тот же пример при одинаковых
(81,6-77,1)
<?m 1 <?ПТ2----— =те,4 Н/см,
<пр, = /пр 2 - • с,.р =0,8 (79,4 tg 1Г + 2-0,0143-0,32-3,14 х X 142®-tg 11° 0,6-3,14-142-1) — 316,4 Нем-=3,164 МПа-см.
Определим перемещение в месте стыка обоих участков но формуле (} 721
1 Г 3,164
До =
2-2,1-Ш-857 1(2,54-10-*)* (1.795- 10Б— 1,306-10*)*
ПРОДОЛЬНАЯ УСТОЙЧИВОСТЬ ЗАГЛУБЛЕННЫХ ТРУБОПРОВОДОВ ПРИ ДЕЙСТВИИ ПОЛОЖИТЕЛЬНОГО ТЕМПЕРАТУРНОГО ПЕРЕПАДА И ВНУТРЕННЕГО ДАВЛЕНИЯ
При действии положительного температурного перепада и внутреннего] давления в ссчевии трубопровода возникает продольное осевое сжнмаюГ щее усилие, которое может привести к выпучиванию подземного труболро! вода. Поэтому при расчете трубопроводов больших диаметров необходимо определять их конструктивные параметры (конфигурацию оси трубопровода^! балластировку трубопровода, его глубину заложения) из условия обеспея чения продольной устойчивости.
Глубина заложения подземных трубопроводов определяется рядом фак-1 торов: технологических, зависящих от транспортируемого продукта; мехай ничсских. связанных с защитой трубопровода от механических поврежде! ний; геокриологических, связанных с взаимодействием трубопровода сгрун-1 том, и прочностных, связанных с продольной устойчивостью л напряжен-} но-деформированпым состоянием трубопровода.
§ 1 Определение критического усилия для заглубленного трубопровода, уложенного с начальным изгибом
Рассмотрим заглубленный трубопровод под действием эквивалента: сжимающих усилий, вызванных повышением температуры и внутренней давления. Расчетные модели грунта, их количественные параметры рассмо^ рены в третьей главе.
Если нсслеловать устойчивость в соответствии с расчетной схемой, пред-1 полагающей, что для прямолинейной формы возмущения сколь угодно малы, то подземный трубопровод можно рассматривать как стер ж ель в лив нейно-упрутон среде, т. е. считать сопротивление грунта пропорцнональ-1 ным перемещению.
Как известно, уравнение равновесия прямолинейного сжатого стержня в линейно упругой среде имеет вид
_, d*v „ cPv , , I
+ ^ °- ,5I> где LI — изгибная жесткость трубы; v —- перемещения сечения х\ S — эк-] вивалентное продольное сжимающее усилие; k — коэффициент пропорцио*1 иальности, равный произведению обобщенного коэффициента нормальпопя сопротивления грунта cvn иа эффективный размер сечения стержня, при-Г пинаемый равным наружному диаметру трубы.
Проведенные экспериментальные исследования устойчивости трубопро-] водов показывают, что искривления прямолинейного трубопровода действи!] тельио происходят при параметрах, определяемых нз решения уравнения (5.1). Однако, как отмечено в работе [49], результаты расчета в соответ-С ствии с уравнением (5.1) даже прп заниженных значениях коэффициента1] постели приводят (почти для всех условий эксплуатации) к выподу о зиа-1 чптелыгом запасе устойчивости подземных трубопроводов В то же время, как показывает опыт эксплуатации трубопроводов, имеются случаи выпут-j чиваиня отдельных заглубленных участков. Кажущееся противоречие межд* результатом экспериментов и опытом эксплуатации связано с неучетом начального искривления трубопровода и фактического сопротивления грунта.I Я М Ясин и В. И. Черникии исследовали [49] устойчивость трубопровода при больших перемещениях. Как показал анализ, в ряде случаев нкж-нее критическое усилие ие является определяющим для подземного трубо^-i
Pi!c 20. Расчетная модель подземного трубопровода прн анализе его продольной устойчивости
Pic 21 Расчетная модель грунта при поперечных вертикальных (вверх) перемещениях трубы
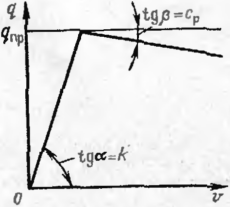
провода. Кроме того, принятая авторами жесткопластичсская модель грунта достаточно условна, так как не учитывает зависимость сопротивления грунта от перемещений, которые могут быть значительными.
Для анализа продольной устойчивости трубопровода с начальным искривлением (рис. 20) необходимо принять модель грунта, учитывающую изменчивость и ограниченность (по значению) сопротивления грунта поперечным перемещениям трубопровода. Для получения решения об устойчивости трубопровода, имеющего начальные искривления в вертикальной плоскости выпуклостью вверх, принимаем бнлииейную модель грунта (рис. 21), характеризующуюся тем, что вначале с ростом перемещений сопротивление грунта возрастает, достигая «предельного», затем при продол жающемся перемещении уменьшается. Угол наклона нисходящей ветви характеризует разрушение грунта засыпки и уменьшения слоя грунта над трубой при вертикальных перемещениях в горизонтальной плоскости.
Аналитическую зависимость сопротивления грунта поперечным перемещениям трубы (см. рис. 21) можно выразить в виде:
q — kv, при 0<ч<9пр/А; (5.2)
q ~ <?пр (1 -{- Ср !k) — СрР, при <?Пр/? <vs(5 3)
rjt (/пг — предельное сопротивление поперечным перемещениям трубы пясрх: cfJ — коэффициент разгрузки; Н—глубина заложения (от верха за сыпь» до нпза трубы).
Одним из наиболее распространенных методов решения подобных нелинейных задач является энергетический метод, основанный на анализе полной энергии системы, в данном случае системы трубопровод —грунт. При использовании этого метода задаются формой полны выпучивания,
2 ее характеристики определяются минимальной энергией по параметрам
вымученного участка. При этом принимается обычно, что формы началь
ного изгиба и дополнительных перемещений совпадают.
Поэтому представляется целесообразным исследовать влияние различных форм начального изгиба и дополнительных перемещений на поведение САатого трубопровода. Для получения достоверного сравнения влияния Рзз.ти'шых факторов используем более точные решения, полученные иа 0С| °ве дифференциального уравнения равновесия. При этом, чтобы полу-11ть решение в замкнутом виде, будем рассматривать только линейную 4с Кль грунта, описываемую зависимостью (5.2).
Уравнение продольно-поперечного изгиба стержня на упругом основа! нин имеет вид j
(5.4)
El
dx4
dx*
dx*
где S — продольное осевое сжимающее усилие в сечении трубы k — коэф! фициепт пропорциональности; v<, и V — соответственно начальный и дополнительный прогибы в сечении.
Рассмотрим две формы начального прогиба трубопровода:
« - '' [sin (-Ь^Н ) + cos (г1—) ]
(5.51
при
. 2 л(х — I)
О s»r ———— 21
(I)
(5.1
‘-о (II)
— оо < х < (- сю;
при Кх<1;
= 0 при />лг>/.
Здесь начало. координат принято в середине кривых, имеющих стрели начального прогиба fo; индексы I и II обозначают соответственно дв^ участка второй формы изгиба.
Первая форма начального прогиба по уравневию (5.5) характеризует! тем, что за «основной» волной длиной 21 в обе стороны от нес распростр| няются быстро затухающие волны с малыми амплитудами. Во второй форме начального изгиба к волне длиной 21 с обеих сторон примыкав полубссконечные прямолинейные участки.
С учетом принятых форм начального прогиба (5.5) и (5.6) было нгД деио решение неоднородного дифференциального уравнения (5.4). Прои вольные постоянные определялись нз граничных условий и условий сопц жепия, которые соответственно дли форм (5.5) и (5 6) имеют biu:
dPv
dxa
dv
dx
dv
dx
лг = О
-О;
О,
ври
(5.7)
О,
0;
при *->ОС
d2v
dv.
dv
II
II
при
dx
dx*
dx
d2v{
dx2
d3v
d'v.
II
(5.8)!
dx»
dx3
dv.
d3Vj
dxa
= 0.
при
dx
По произвольным постоянным определили форму дополнительных перемещений трубопроводов, а исходя нз известного соотношения "между изгибающим моментом и перемещением М= Eld2v/dx2, получили распределен ине изгибающих моментов по длине.
В соответствии с изложенным алгоритмам расчета с помошью ЭВМ вычислены перемещения и изгибающие моменты для стрелки начального прогиба 1 при различных значениях продольного усилия S и длины волны I Решение выполнено в безразмерных параметрах: /о /r./i — отноше-
с стрелки начального прогиба к радиусу инерции сечения трубы;
5 = S 2 ¦yjElk— отношение продольного усилия ft критической силе для
(^конечной балки;
г./ я4 —отношение длины полуволны изгиба к длине полуволны,
соответствующей потере устойчивости бесконечной балки.
Вычисления выполнены только для одной стрелки начального прогиба, так как все вычисленные характеристики прямо пропорциональны ее зиа
ценила рИС 22 и 23 приведены вычисленные безразмерные параметры мак^ симального значения прогиба /=//f _и изгибающего момента М = M/2i ¦y/Elk для стрелки начального прогиба /о= 1 при трех значениях продольного усилия S. Решения для первой формы начального прогиба по уравнению (5 5) показаны на рисунках пунктирными линиями, для второй по уравнению (5.6) — сплошной.
Анализ результатов показал следующее: наибольшие поперечные перемещения и изгибающий момент находятся в середине кривой (х=0); для второй формы начального изгиба поперечные перемещения наблюдаются н на первоначально прямолинейных участках трубопровода; зависимость наибольшего перемещения от длины начальной полуволны имеет максимум; длина полуволны, соответствующая максимальному значению прогиба, не зависят от продольного усилия, а определяется соотношением жесткости трубопровода и среды (грунта); изгибающий момент, как и следовало ожидать, уменьшается с увеличением начальной длины волиы; дополнительные прогибы и изгибающие моменты для обеих форм начального прогиба близки Друг к другу. Это позволяет сделать вывод о том, что форма начального прогиба мало влияет на поведение подземного трубопровода при действии продольного усилия; определяющими являются амплитуда и длина волны начального прогиба.
С использованием энергетического метода также проанализировано влияние различных форм дополнительных перемещений иа поведение сжатого трубопровода. В той же постановке задачи и при тех же принятых обоз-
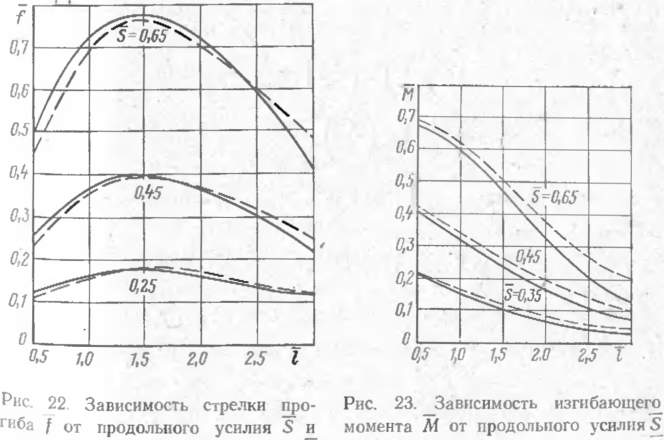
Длнны волны начального изгиба I и длины волны начального изгиба I (по уравнению равновесия) (по уравнению равновесия)
иачениях полная энергия системы трубопровод — грунт при действ: продольного усилия будет
Принято, что длина деформируемого участка при нагружении оста ется постоянной, х,, х2 — соответственно! абсциссы начала и конца этом участка. Начальную форму изгиба трубопровода принимаем, как и ранее по уравнениям (5.5) и (5.6). Формы дополнительных перемещений для каждого из случаев Запишем в виде:
-
2)
№ = ^ j;
[n(x I-1) •[.
L 21 J’
3) Vs — fj sin®
4) = /sin* J
Л ^2f~} '
(5.1^
Вычисляем энергию системы в соответствии с выражением (5.9) формах дополнительных перемещений по (5.10). Далее, из уравнення р, новесня, полученного из условия равенства первой вариации полной эи гии нулю (дЭ/д{=0), будем иметь зависимость между стрелкой допо. тельного прогиба и продольным усилием
|
>нер
...
fi—fo , ч , (5.11
(Л/S)- 1
где величины А и В вычисляются для формы начального изгиба по уравнению (5.6), а дополнительного но (5.10) следующим образом:
I (0,375Т), В3 = 0,935;
|-(0,28/2), е4 = 0,845. (5.12;
Здесь индексы прн коэффициентах А и В соответствуют индексам при пв> ремещеииях v.
Максимальный изгибающий момент определяется по формуле
где коэффициент С, имеющий тот же индекс, что А к В, равен-
Сг =- —~; Сг — 0,5; С3= 1; С4 =1,5 (5.14)
я *
Рис. 24. Зависимость стрелки прогиба j от продольного усилия S и длины волны начального изгиба I (по энергетическому методу)
1 4 — кривые, построенные для различных форм перемещения по (5.10)
Рис. 25. Зависимость изгибающего момента М от продольного усилия S и длины волны начального изгиба / (по энергетическому методу)
1—4 — то же. что на рис. 21
Аналогичным образом вычислены максимальные дополнительные перемещения и моменты для формы начального поогнба по формуле (5.5), а дополнительного по формуле (5.7).
Полученные результаты для различных форм начального и дополнительного прогибов при параметре продольного усилия S=0,45 и стрелке начального прогиба /0=1 приведены на рис. 24 и 25. Сплошными линиями, как и ранее, показаны результаты, полученные при начальной форме прогибов по выражению (5.6), пунктирными — па выражению (5.5). Цифровые индексы кривых соответствуют различным формам дополнительных перемещений по формулам (5.10).
Приведенные кривые подтверждают предыдущий вывод о том, что форма начального изгиба незначительно влияет на прогиб н изгибающий момент, а форма дополнительных перемещений оказывает существенное
в.’ ияние иа эти показатели, особенно на изгибающий момент.
Для сравнения на рис. 24 и 25 построены кривые (без индексов) по результатам, полученным из решения уравнення равновесия. Из графиков следует, что все решения, основанные иа энергетическом методе, дают ту же качественную зависимость прогиба и изгибающего момента от длины начальной волны, что и решение уравнения равновесия. Кривая прогибов также характеризуется наличием максимума. Значение /, при котором имеет '•есто этот максимум, не зависит от формы начального изгиба и лежит п интервале 1 —1,73 в соответствии с принятой формой дополнительных m I емещеиий-. Кривая изгибающих моментов также имеет монотонный характер, а Изгибающий момент уменьшается с увеличением длины волны.
С количественной точки зрения наибольшее совпадение результатов в облд.' сти максимальных перемещений имеет место для формы дополнительных перемещений, описываемой четвертым уравнением (5.10).
Так как форма начального прогиба мало влияет на результаты рас-! чета, то при исследовании устойчивости трубопровода с учетам нелние» ности диаграммы «сопротивление грунта — перемещение» будем считать, что начальная форма прогиба совпадает с формой выпучивания.
Определим форму волны выпучивания при малых перемещениях, рассматривая трубопровод как сжатый стержень в упругой среде. Учитывая, что жесткость грунта засыпки значительно меньше жесткости основания,! и анализируя случаи выпучивания трубопроводов, можно принять, что при, перемещениях трубопровода в вертикальной плоскости образуется одна волна выпучивания, примыкающие участки остается прямолинейными, а по концам волны угол поворота и изгибающий момент равны иулю, т. с,
v=f sin3 —— . (5.17)
Иными словами, мы считаем, что форма начальной волны совпадает с формой выпучивания трубопровода в процессе деформации и что едицГ ственным наперед заданным параметром является стрелка начального npo-J гиба f0.
При выпучивании подземного трубопровода сопротивление грунта вер-j тикалышм перемещениям (см. рис. 21) описывается в соответствии с вы ражешгем (5 2) на первом участке длиной а и выражением (5.3) на вто-1
ром участке волны выпучивания длиной l—a [см. рис. 20). В дальяейшеЩ
так как сг, отношением cvjk пренебрегаем.
Определяем полную энергию системы трубопровод — грунт при поперс» ных перемещениях (см. рис. 20)
0 0 1 a I
+ k J t)sdx -f- J (q,tp- -cpv)v dx. (5.18)
0 a
Здесь для интенсивности поперечных нагрузок принят множитель '/г, ] так как эти интенсивности прн переводе балки из нагруженного состояния 1 в первоначальное обращаются в нуль и, следовательно, по природе своей] должны быть отнесены к категории внутренних сил.
w
Поставляем и выражение (5.1) уравнения начального и дополнительного прогибов (ЬЛ 6), (5.17) и после интегрирования получаем
2
Э=^Ъ2~ (?2 + ЧЫ + P®i («) + № <«> -
т2
--jT?(-7-^ и), (5.19)
где
, , . яп 1 1 лп . , яп
Ф, (n) ----sin nn--cos-sin3---
Ф2 («) — cos —sin2 —-—2 cos ——. (5.20)
В формулах (5.20) и (5 21) введены следующие безразмерные величины
256/»
my^So/hiq — параметр продольного усилия; Х=5 n*Ell4PNq—параметр длины выпученного участка; ту= 10¦yEtk/SNq —характеристика упругой работы грунта; тр=10 V EIcp/3Nq — характеристика зоны разгрузки, где
/V, V^SFT (5 21)
Относительная длина участка упругой работы грунта определяется из условия, что v(x=a) =qnv!k
nn = 2 arcsin |/” 100/9my?_
Условию равновесия системы соответствует равенство нулю первой вариации полной энергии. Исходя из этого, определяется зависимость между продольными усилием и перемещением:
т„ — - ¦
-г— Фа (я)--ЯП sin*- — —- X
27пХ? L 2 2 J п>.
X [— — 0! (л)--я?п' sin* -— j; (5.22)
Зл? К(Э^/ЮО)2'3-]
Длина волны выпучивания, соответствующая минимальному значенЯ продольного усилия, определяется из условия rfm0/rf/.=0
_ Построим диаграмму зависимости полного прогиба от продольного yJ лия в соответствии с выражениями (5.22) и (5.24). Несколько кривых ра повесных состояний при различных стрелках начального прогиба ?о и Л рактернстиках грунта приведены на рис. 26. (Программирование и расЦ На ЭВМ выполнены инж. М. И. Купниым). Следуя классификации, пр ложенпой Я. Г. Пановко, мы имеем потерю устойчивости второго ра которая характеризуется неизменностью (в качественном отношении) ка фигурации системы в процессе ее постепенного нагружения, существованш максимума нагрузки (критической силы второго ряда) и отсутствием pi ветвления форм устойчивого равновесия.
Нетрудно показать, что часть (где dm0/W?>0) кривой равновесных ] стояний (см. рис. 26, сплошная линия) является устойчивой. Иссле! полную энергию системы (5.19), получаем, что для этой части кривой Л рая вариация полной энергии положительная, для правой (рис. 26, пу! тнрная линия) — отрицательная, точке соединения соответствует нуле! значение.
На рис. 27 приведены подсчитанные значения продольного критическа| усилия в зависимости от параметра, характеризующего упругую рабой грунта. Значение mKV соответствует экстремальному значению т0, опрел
Щ
15
2,0
1,5
1,0
0,5
|
„ / | \ | |||||||
|
7 | ||||||||
| й II ё” |
||||||||
| О" |
____ | |||||||
| ---* — |
||||||||
| ii | h | |||||||
|
1 | ||||||||
0,5 1,0 1,5 2,0 2,5 3,0 3,5 С0+К
Рис. 26. Диаграмма «полный прогиб — продольное усилие» с учетом упругой и упругопластической работы грунта
„яеМОмУ выражениями (5.22), т. е. ‘ очке соединения ветвей (см. рис. 26). ?ак следует из графика (рис. 27)
малых начальных стрелках про-
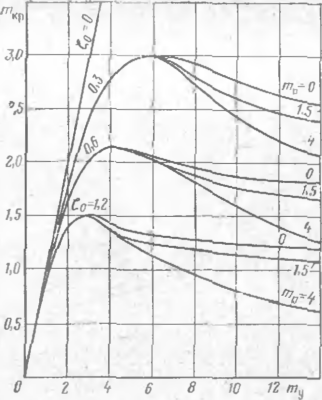
Рис. 27. Зависимость параметра продольного критического усилия от параметра упругой работы грунта при различных значениях начального прогиба
гнба fef параметр упругой работы [>\нта ту имеет значительное влияние на критическое усилие, что соответствует результатам экспериментов П. П. Бородавкина и rj И. Быкова. Если считать, что па всем участке выпучивания грунт работает только в упругой стадии, т е. принять л-1, то критическая сила, как это следует из выражения (5.22) будет m„p=my, что совпадает с решением (5.15). При этом кривая равновесных состояний имеет асимптоту шо=/якр и аналитическое выражение этой кривой принимает
ВИД
При больших значениях начального прогиба н параметра ту влияние упругой зоны работы грунта иа продольное критическое усилие не значительно (см. рис. 27), однако прп этом сказывается влияние зоны разгрузки. Если пренебречь влиянием упругой работы груита, т. с. считать л=0, то из (5.22) можно получить решенне в замкнутом виде
1
(5 26)
т«Р —
27пСо
1 +
640
160
27п?
Минимальная длина волны и стрелка выпучивания, соответствующие потере устойчивости, определяются по формулам:
_2
(5.27)
"кр
27я?о
1
?кр — ¦
(5.28)
1/?о + 27л/Лр/320
График рис. 28 показывает, что начальный изгиб, определяемый в данном случае начальной стрелкой прогиба ?0, снижает силу выпучивания по сравнению с критической нагрузкой, полученной при неучетс начального изгиба.
Достаточных статистических данных о начальном изгибе подземных трубопроводов в настоящее время не имеется. В практике проектирования магистральных трубопроводов первоначальная кривизна обычно определя ется только радиусом изгиба. Для перехода от известных радиусов изгиба к начальной стрелке прогиба нами с помощью ЭВМ исследовалось влия-Ние распределения начального прогиба По длине участка выпучивания на поперечпые перемещения сжатого стержня в упругой среде. Анализ показал, что при практических расчетах трубопроводов на действие продольных усилии можно считать, что нача иий изгиб распределен по Л длине, а его форма близка к син| соиде. Тогда зависимость мел стрелкой начального прогиба и ра диусом изгиба можно вырази в виде

Рис. 28. Диаграмма «критическое продольное усилие — начальный про-гиб»
(5S
где ро — безразмерный радиус изги| равный
РО - Ро V W'*7? (Е 30 При определении и исследои нил полной энергии системы пр дольное усилие S0 принято посто^ ным по длине и независимым длины и стрелки волны вылучд ния. Продольное же усилие от грузки (повышения температуры внутреннего давления) определ иа основе нелинейной зависимо между усилием и перемещен^ учитывая сопротивление грунта пр дольным перемещениям на прямол некных участках, примыкаюц к месту выпучивания.
Величина Sa представляет соб алгебраическую сумму воздейст продукта иа заглушку P»=pf (Кв — площадь трубы в светД продольного усилия N о в стенках трубы, вызываемого деформацией тру1’ провода под действием внутреннего давления и температуры:
о
Деформация изгибаемого Элемента связана с перемещением нелинейно зависимостью
= —-f. —f-dx 2 \
(5 34
Соотношение термоупругости для продольной деформации имеет вид Eje = N0/EF + <хЫ — цоКц /Е (5.35J
(At положительно при нагревании).
Сравнивая (534) и (5 35) и учитывая, что для тонкостенных труб r-2PjF, получаем
1 • [aStEF -{- Ps (1 — 2(i) — S0] —
dx EF
i [d(V+Vo> v; » г л* v _____
- T1 dx J + TI it) ¦ (5 36)
Произведя интегрирование в соответствии с (5.33), с учетом начальной формы изгиба (516) и выпучивания (5.17), имеем
«х = д1 [aMEF — Я3(1 — 2ц) — S0J. (5.37)
EF
гж
Al^l28T(/M 2/М' (5 38)
Продольное перемещение прямолинейного трубопровода, примыкающего к участку выпучивания, онрецеляется в соответствии с рен ением гл. 4. Используя условие неразрывности (5.32) получаем уравнения для определения продольного усилия в зависимости от нагрузки:
прп отсутствии участка предельного равновесия грунта прн продольных перемещениях
(5-39)
прн наличии участка предельного равновесия грунта
(5.40)
V2/2
Критерием отсутствия участка предельного равновесия грунта при продольных перемещениях является условие
~(тР.Т~т о)<]- (5.41)
Здесь приняты следующие обозначения: mp. T=\ui\IEF-\-P^(l—2n)]jNq—
параметр нагрузки; >c=/n])//,Vs — характеристика работы грунта участка пре-
_ 9
дельного равновесия прн продольных перемещениях; ^2(?2+2??0) —
Соразмерное удлинение участка выпучивания.
Проанализируем влияние начального прогиба и примыкающих к месту выпучивания прямолинейных участков на продольное усилие, вызванное изменением температуры и давления, рассматривая трубопровод как стержень в упругой среде, сопротивление которой вертикальным перемещением — величина неограниченная. Тогда с учетом (5.25) находим
&*кр[—-т;--О- (5-42)
Д,
1 320
Уравнение (5 39) является нелинейным относите, ьно тс, Так как вели-•чна Л,, определяемая в этом случае но (5.42), есть функция то. Уравнение (5.39) можно решить графически. На рис. 29 приведен график, построенный в соответствии с уравнением (5.39) и с учетом (5.42). К л к ледует из графика, для прямолинейного трубопровода (?и 0) или
в общем случае при отсутствии сопротивления грунта продольным перемен ниям трубопровода (\’/=0) т„=тр, г.
С увеличением стрелки начального прогиба параметр mo/m к р уменыц] ется. Увеличение степени защемления трубопровода yl также вызыва? уменьшение т0, т. е. полное продольное сжимающее усилие изменяете! от S0—a&iEF+Pa(l—2ц) лри ?о=0 до S0= О при go—>«>, а продольный осевые напряжения в стенках трубы согласно (5.31) от температурного не репада изменяются от айtE до нуля, а от внутреннего давления от 0,3oj^ до 0,5 Окц,
Уравнение (5.39) или (5.40) позволяет по известному значению кя_ тического продольного усилия тс = тКр определить соответствующую кри тическую нагрузку m„t Т. В этом случае при определении Ai значений волны выпучивания Я, н стрелки прогиба ? необходимо принимать равньи) соответственно Акр и ?кр. Так как величины /.кр и С«р зависят только начальной стрелки прогиба и параметров грунта, то уравнения (5.35)
(5.40) становятся линейными относительно то=ткр.
Рассмотрим работу наземного трубопровода.
Остановимся на потере устойчивости наземного трубопровода, уложе ного в насыпи с изгибом в горизонтальной плоскости. Расчетную моде грунта здесь можно принять аналогично приведенной на рис. 21, одна она будет справедлива при перемещениях трубы как вправо, так и вле в горизонтальной плоскости от первоначальной осн. На рис. 30 прнведеЛ зависимости параметра критического усилия тКр от относительной стрелй_ начального прогиба при различных формах потери устойчивости. Гря
фики построены для параметров ту =4 и тР — \. Сплошными линиями по казаны результаты, соответствующие потере устойчивости, происходящей форме дополнительных перемещений, отвечающей сниусоиде первой степ^Г (пдоп=1), пунктирными — синусоиде третьей степени (ядоп=3). Каждая из' трех линий соответствует одной из форм начального изгиба (лнач= 1-т-3)< Как следует из графика рис. 30, форма начального изгиба мало
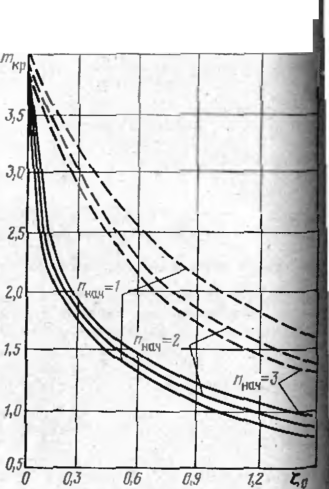
Рис. 30. Влияние форм потери ус- ^ тойчнвостн на критическое усилив!
влияет на критическое усилие, опре деляющим является форма дополнительных перемещений.
Очевидно, что условиям работы наземного трубопровода в насыпи с изгибом в горизонтальной плоскости (ввиду одинаковой жесткости грунта в этой плоскости) из рас-
0,6
0,4
0,2
Рис. 29. Изменение продольного усилия в зависимости от стрелки на чальиого прогиба
I
ПТд
%
OS
|
%__^ | AfV УЧ | гт7ъ |
|||
| • |
ЛУ // | Гг1"— |
|||
|
" и3 | |||||
0 0,2 0Л 0,6 0,8 глрт/т^
отрсниых форм потери устойчивости более полно отвечает синусоида первой степени (идоп=1). Этой форме (см. рис. 30) соответствует меиынее значение критического усилия.
Из приведенного анализа следует, что для подземного трубопровода начальным искривлением в вертикальной плоскости выпуклостью вверх и1Н для трубопровода в насыпи с начальным искривлением в горизонтально?! плоскости характерна потери устойчивости второго рода, которая характеризуется неизменностью (в качественном отношении) конфигурации системы при нагружении и наличием максимума нагрузки. При малом начальном прогибе критическое усилие определяется в основном упругой работой грунта, классическое решение здесь соответствует прямолинейной начальной фо»ме; при значительном начальном прогибе влияние упругой работы грунта па критическое усилие незначительно, определяющим является пластическая стадия работы групта.
§ 2. Упрощенные зависимости для практических расчетов
Так как решение в замкнутом виде можно получить только для частных случаев, то для практических расчетов по рекомендациям ВНИИСТ используются упрошенные зависимости, полученные с допущениями, идущими в запас устойчивости. Приведем необходимые расчётные формулы.
Критическое продольное усилие для прямолинейных участков заглубленного в грунт трубопровода определяется по формуле
пч:1 Cy<PAv
N*P — ~Г2— +" 7~ * (5 43)
312
где с.у о — коэффициент нормального сопротивления грунта.
Расчетная длина волны выпучивания, соответствующая минимальному значению критического усилия:
| / Е!
' П V CyoDH '
?кр — 31 \/ с^ор ¦ (5'44)
Подставляя значение в (5.43), получаем минимальное значение критического продольного усилия
Л^кр — ^ -y/cyoDHEI. (5.45)
Критическое продольное усилие и расчетная длина волны выпучивания
для подземных участков трубопровода с углами поворота, обращенными
вып>клостью вверх, соответственно будут:
<7прРо (• + л!• + —
v V q„vPl J
где Ро расчетный радиус оси изгиба трубопровода.
Исходя из расчетного радиуса оси изгиба минимальное значение критического продольного усилия
Л^кр — 0,375gnpp0, (5.48)
ГЯо ^пр — предельное сопротивление поперечным перемещениям трубопровода вверх.
Дополнительная стрелка прогиба, соответствующая потере устойчи вости:
t fl> . ( ¦ /кр > /о — - . (5.49)
<?11р
где Ср — параметр разгрузки грунта.
Для наземного трубопровода, уложенного в насыпи, с изгибом в го: рнзонталькой плоскости параметры те же, что и для уложенного в грун! трубопровода:
п8Е/ cpLk
lL п
Стрелка дополнительного прогиба вычисляется по формуле (5 49).
Как отмечалось, эквивалентное сжимающее продольное осевое у ил» обусловлено изменением температуры и давления и зависит от деформа-тивиости системы. Как показал проведенный анализ, при малых начальны искривлениях перемещения системы незначительны и эквивалентное сжимаю Щее Усилие можно определять без учета дсформативности системы.
При расчетном радиусе изгиба 1 ООО DB эквивалентное усилие
5Эко = 50 = (аМЕ + О,2<гкц) F, (5.53;
где &( — температурный перепад, положительный прн нагревании; окц
кольцевые напряжения от внутреннего давления.
При меньшем расчетном радиусе (p0=g;1000 DH) эквивалентное продоль-^
ное усилие вычисляется по формулам, учитывающим продольные связи и
«самокомпенсацию» системы: а) при выполнении условия
^—s=l, (5 54)
х 1 + 2/р ^
т. с. при отсутствии участка предельного равновесия грунта при продоль'1
пых перемещениях трубопровода
где
32L-kP
б; при невыполнении условия (5.54), т. е при на пиши участка пре-дс ibiioro равновесия грунта при продольных перемещениях трубопровода
В приведенных формулах начальный изгиб заглубленного трубопровода характеризуется расчетным ради}сом р0- В соответствии с принятой постановкой задачи под расчетным радиусом Ро понимается минимальный радиус изгиба оси трубы, ес.ш изгнб имеет место иа всей длине волны выпучивания. Это обычно наблюдается при свободном (упругом) изгибе тр\бы. Таким образом, если длина хорды кривой больше или равна критической длине волиц выпучивания, то в качестве расчетного радиуса принимается фактический ради ус оси изгиба трубы т. е.
при 1крг^2р5]'я-^- ро = Р> (5.59)
где р — минимальный радиус оси изгиба трубы; а — угол поворота оси трассы трубопровода. «
В практике проектирования и строительства трубопроводов их поворот может выполняться с применением отводов (колен) машинного гнутья или сварных (рис. 31). В этом случае, обычно, условие (5.59) не соблюдается, т. е. перемещение трубопровода происходит по длине, включающей и примыкающие к отводам первоначально прямолинейные участки. Тогда, зная длину волны выпучивания, расчетный радиус можно определить как радиус кривой, проходящей через начало н конец волны выпучивания и вершш у угла поворота. Так как ДЛИ1 а волны выпучивания зависит от расчетного радиуса оси изгиба, то решение выполняется методом последовательных приближений Вначале задаемся возможной длиной волны выпучивания, примерно (40—70) ?>и.
В зависимости от схемы прокладки по формулам (5.60)—(564) определяем расчетный радиус р0 Далее, по формуле (5.47) или (5.51)
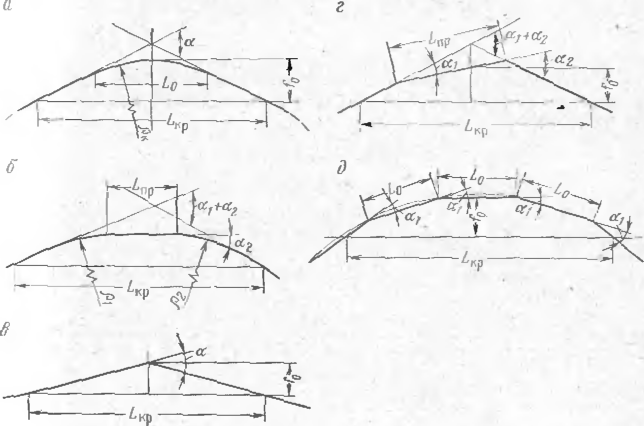
определяем расчетную длину полны выпучивания. Для второго приближения! принимаем возможную дляну волны выпучивания как среднее значение между предшествующим и вычисленным. Обычно трех-четырех прнближёГ ний достаточно для определения расчетного радиуса, зная который п<И (5.48) или (5.52), определяем критическое продольное усилие и, по (5.5)] или (5.58),— эквивалентное продольное усилие.
При прокладке подземного трубопровода по схеме (рис. 31,а), когда' угол а^9'\ длина хорды кривой менее длины волны выпучивания и длина j каждого из прямолинейных примыкающих участков Lnp такова, чщ
JKp
расчетный радиус изгиба определяется по формуле
2L® cos — КР I)
(5 60)
n2j^LKP sin ---2ркр^1 — cos
где а — угол поворота трубопровода в вертикальной плоскости, градусы;] Ркр — радиус изгиба бен (кривой), см; LKр—расчетная длина волны вь пучпнания, см.
При прокладке подземного трубопровода но схеме (рис. 31,6), при] которой расчетный участок состоит из двух кривых вставок и прямолиней-
«1
ного участка между ними, причем каждый из углов менее 9° и PiSin ——
а2 _
+ p2sin —+ Lr.p-". ?-кр> расчетный радиус изгиба определяется по формуле}
2Li
кр
(5-61)1
Ро
Я2 |^кр tg ~i~-- ^inp + Pi tg I Ps tg
(sin _ tg «L±«S. coS -M]
При прокладке подземного трубопровода по схеме (рис. 31, в), при которой на расчетной длине лишь один угол поворота, выполненный с по-1 мощью колен радиусом не более 5 Du, расчетный радиус изгиба определяется по формуле
Ро= -2LkP •
(5.62) I
При прокладке подземного трубопровода по схеме (рис. 31, г), при которой на расчетной длине имеются два угла поворота, выполненные! с помощью колеи (причем Рк^5?)н), расчетный радиус изгиба определи-, ется по формуле
2 L2
LKp
Ро —
Oa —a, . a,+a2 Oj-a,
я2 ^кр tg j-”2 -f
I,lp ^sir
Если при прокладке трубопроводов кривая заменяется ломаной линией с одинаковыми углами, образованными коленами Рк^5?>в и а=3ч-6°, и
с равным» расстояниями между ними (рис. 31, д), то расчетный радиус
изгиба определяется по формуле
л г 9 па*
2LKP c0S -ф-
Ро =---- . (б. 64)
л2 ^-кр sin --L0(n~~ 1) sin «!
Отметим, что эти расчетные формулы не учитывают влияния примыкающих к рассчитываемому участку трубопровода углов поворота противоположного знака, что идет в запас продольной устойчивости.
Чтобы получить решение, удобное для ручного счета, принят ряд допущений и гипотез, которые не позволяют учесть разнообразие расчетных схем. Например, рассматривается только случай, когда сопротивление по перечным перемещениям трубы одинаково по всей длине полны выпучивания. При закреплении газопровода против выпучивания анкерами или грузами рационально их размещать не равномерно по длине волны выпучивания, а сосредоточивать вблизи вершин углов поворота. Расчетные формулы для этой схемы прокладки получены из условий равенства работ на дополнительных перемещениях поперечных пагрузок.
Если обозначить удерживающую способность в окрестности вершины
на длине а через <?2. а на примыкающих к вершине участках — Я\, то от
носительная Длина, на которой необходима прнгрузка ц2, определяется из решения
п = — arcsin -—, a nLKp • (5.65)
п Чг — *?i
При этом должны соблюдаться условия c/i и Экономия полу
чается за счет того, что во всех случаях
9пр^кр ^ (?кр — я) + Ч-iO. (5.66)
Величина <?пр определяется из условия продольной устойчивости тру
бопровода в предположении равномерной нагрузки по всей длине волны выпучивания.
§ 3. Экспериментальные исследования продольной устойчивости заглубленных трубопроводов
Одни из способов проверки полученных качественных и количественных результатов по расчету продольной устойчивости подземных трубопроводов — анализ опыта эксплуатации.
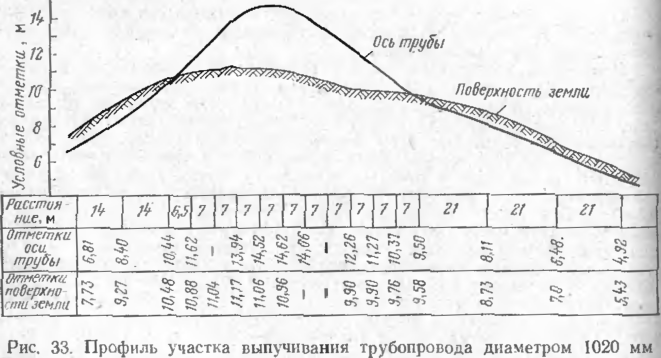
Нами была обследована система газопроводов, проложенных в районах Средней Азии, и проанализированы случаи выпучивания отдельных участков. Качественный характер выпучивания примерно одинаков (рис. 32). Для газопровода диаметром 1020 мм длина волны выпучивания составляла 65—30 м. При этом чем меньше был первоначальный радиус Упругого изгиба, тем меньше была длина волны выпучивания. Для газо проводов, проложенных с отводами машинного гнутья, длина волны выпучивания составляла всего 30—35 м, стрелка прогиба при вышучивании — 0,8—3 м. Рассмотрим случай выпучивания подземного участка газопровода диаметром 1020 мм иа расстоянии около 10 км от компрессорной станции (рис. 33). Газопровод проходит по участку, сложенному сухими пылеватыми песками барханного типа. Высота засыпки на примыкающих к месту выпучивания участках составляла 0,2—0,3 м. Из информации эксплуатирующей организации известно, что при работе первой очереди компрессорной станций, когда температура газа на данном участке составляла 34 С, глубина заложении трубы (до верхней образующей) в среднем была

Рис. 32. Характер выпучивания подземного трубопровода; а участка с упругой кривой, б — участка с кривой машинного гнутья
0,3 м. Используя результаты геодезической съемки примыкающих к месгуа выпучивания участков, можно предположить, что радиус изгиба оси трубы в вертикальной плоскости составлял примерно 1000 м. С пуском второй очереди компрессорной станции температура газа повысилась до 43 °С, на участке кривой началось выпучивание на длине 15 м и стрелка изгиба со-!' ставила 30 см. В дальнейшем при пуске компрессорной станции на пол-1 ную мощность температура газа возросла до 48 °С, при этом продолжалось дальнейшее выпучивание и стрелка изгиба увеличилась до 308 см, а длина приподнятой части достигла 66,5 м.
Проведем по изложенным расчетным формулам количественную оценка этого случая, используя определенные нами физико-жхаинческнё характе-] ристики грунта: объемный вес грунта >’^=15,4 Н/м3, угол внутреннего тре-1 ния фгр 16°, сцспленне сГр=0 Предельная удерживающая способность! против поперечных перемещений <7Пр = 118 Н/см, коэффициент разгрузки) ср=9,1 П/см2. Критическое продольное усилие по (5.48) составляет Лг1[р =1 =4,42 • 106 Н, критический температурный перепад Дt„p по (5.53) равен :
50,5 °С. Учитывая, что данный участок монтировался в декабре при тем-, пературе примерно —5 °С, можно считать, что фактический температурный j перепад близок к расчетному.
рассмотрим также случай выпучивания открытого трубопровода, описанный Э. М. Ясиным в работе [49]. Трубопровод сечением 529 x9 мм находился в открытой траншее, при температуре 33 °С он выпучился. Опрс-'1( нм по ранее приведенным формулам расчетный радиус возможного упругого изгиба. По формуле (5.33) фактическое критическое продольное усилие Лкр = 1,24 • 106 Н, радиус упругого изгиба, при котором может произойти выпучивание, по формуле (5.48) будет р=2820 м. Данный радиус первоначального изгиба оси трубы соответствует 4300 диаметрам трубы, т с. почти прямолинейному участку.
Для анализа ряда допущений и гипотез, выявления типа потери устойчивости, а также количественной оценки результатов было проведено экспериментальное исследование поведения модели подземного трубопровода при действии продольного сжимающего усилия.
Трубопровод сечением 219X6 мм был уложен в траншею соответствующего очертания и состоял из двух прямолинейных участков длиной 29,8 м и 31,2 м с каждой стороны от расположенного в средней части сварного колена рi,=40 Da с углом поворота 7°5д'. Высота засылки (до верхней образующей трубы) составляла А=80 см, грунт песчаный с \гр= 17,4 кН/м3 и (рг)1=33°. Концы трубопровода заглушены и усилены против смятия спе-циа. ьпыми ребрами. По концам трубопровода устроены бетонные упоры, рассчитанные на восприятие сдвигающего усилия” до 2000 кН. Уенг." е иа заглушенные торцы трубопровода передавалось двумя гидравлическими домкратами ДГ 100. На каждом этапе иа!ружеиия после соответствующей выдержки нагрузки фиксировались вертикальные поперечные перемещения но длине трубопровода и продолыые перемещения концов.
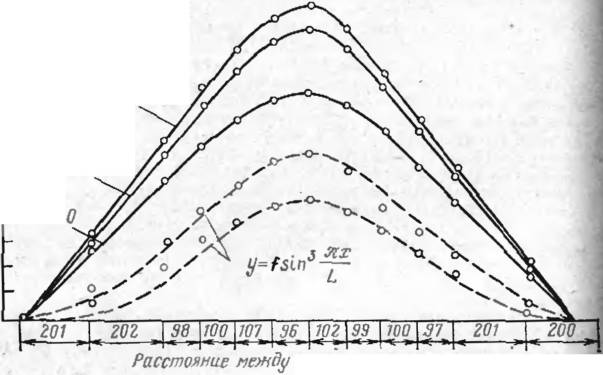
Экспериментальная зависимость продольного усилия от прогиба (рис. 34) совершенно четко фиксирует наличие максимума нагрузки, соответствующего конечному перемещению, т. е, полностью подтверждается то, что для подземного трубопровода, имеющего искривление в вер икаль-
I ой плоскости выпуклостью вверх, характерна потеря устойчивости второго рода.
На рис. 35 приведены упругие лилии подземного участка трубопровода
рн действии продольного усилия. Как следует из результатов опыта,
форма дополнительных перемещений, принятая при анализе устойчивости | о формуле (5.18) и показанная иа рис. 35 пунктиром, согласуется с результатами эксперимента.
Перейдем к количественной оценке результатов эксперимента, определяя расчетные параметры груита (предельные сопротивления, коэффициенты постели н разгрузки) по ранее приведенным формулам: qпр 104,8 Н/см,
1,1 Н/см2, ft=4,6¦ 21,9 100 П/см2, *пр 30,6 Н/см."
Задаемся длиной волны выпучивания LKг, 20,0 м, по (560) находим Ро=60,6 м, по (5.47) определяем соответствующую ZItp=21,2 м, во пто~ ром приближении задаемся LKp 20,9 м, по (5.60) р0 63 4 м, по (5.47)
21 м, т. с. расчетная длина волны выпучивания LKi>=20,95 м. Полу-
четная длина волны выпучивания будет 16.0 м, т. е. расхождение состав
ляет 30,8%- Экспериментальная длина волны выпучивания определялась как расстояние между сечениями, где наблюдались поперечные смещения. Так как точность измерения перемещений составляла 5 мм, то этим, по-видимому, объясняется меньшее экспериментальное значение длины волны выпучивания по сравнению с теоретическим.
Критическое продольное усилие прн Lxp~ 20,95 м но формуле (5.46) будет JV„p=245 кН. Фактическое значение критического продольного усилия, равное разности между максимальным усилием, приложенным к торцу трубопровода, и сопротивле 1ием грунта продольным перемещениям по длине трубопровода, составляло 349 кН, т. е. на 30 % выше расчетного. Большее экспернменталы ое значение по сравнению с расчетным объясняется не только тем, что в последнем для получения более простого решения не учитывается влияние упругих деформаций грунта, но и тем, что предельные сопротивления грунта несколько меньше фактических. Отметим, ‘•то критическое усилие, определенное исходя из линейной модели груита
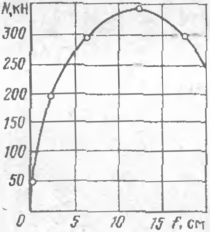
Рис. 35 Упругая линия подземного трубопровод при экспериментальном исследовании продольно!
устойчивости:
- полный прогиб;---- дополнительный прогиб-]
отметший, см
^гго~
о _
*270 -%200-|
5г 130 -
•О
ч 180
Я
по
N=289*tt ЗЬэ
Рис. 34. Экспериментальная зависимость прогиба от продольного усилия
по известной формуле NKP — 2 Y^Eik, превышает фактическое более чев в 12 раз.
Таким образом, на основании проведенных во ВНИИСТе экспериментов, теоретических исследований продольной устойчивости и анализа слу1 чаев выпучивания отдельных участков магистральных трубопроводов изло| женную методику расчета продольной устойчивости подземных трубопроводов можно рекомендовать для использования при проектировании. Пря этом следует иметь в виду, что данное решение дает некоторый запас по продольной устойчивости трубопроводов. Так, с целью получения решения в замкнутом виде упрощена расчетная модель грунта, не учитывается изменение продольного усилия по длине участка выпучивания и использован приближенный энергетический метод. Более точные результаты можно по лучить с использованием разработанной программы расчета на ЭВМ, алгоритм которой изложен в гл. 6.
Пример 1 Определить минимальную глубину заложения газопровода проложенного с упругим изгибом выпуклостью вверх р=1250 м из условия продольной устойчивости. Трубопровод диаметром 1020x12 мм (плСЯ Щадь F=380 см2) проложен иа участке II категории, рабочее (норматив^ мое) давление р—5,5 МПа, температурный перепад At—57 °С, грунт — су-.
nefb со следующими характеристиками: сгр=0,001 МПа 0,1 Н/см* <prP=6°, J 14,3 к Н/м3, вес единицы длины газопровода 9тр=29,80 Н/см
1 Для определения глубины заложения записываем предельное состояние п0 устойчивости, установленное СНиП П-45—75; критическое усилие — по лппмуле (5.48); предельное сопротивление грунта поперечным перемещениям " п° (3-25). ^
Исходя из этих зависимостей, необходимую высоту засыпки от верх-лей образующей до оси трубы определим по формуле
— B-J-V В2+4АС
А = \vp tg 0,7фгр;
В = TrpD,, -f--—р—; С = О.З&угрОи + -¦ — *LZE...
соз0,7фгр 0,375mpnrp пгр
Здесь
S ^aAfg-f 0.2 (l2 10~е-572,1-104-0,2 j x
X 380 = 7,366 10« мПа см2 = 7,366-10* H;
Qn. xp = Qrp + »10°PDeh - 2980 + 0,95'-100-5,5-0,9962 =
(где n — коэффициент перегрузки, равный 0,95).
Тогда
А - 14,3-Ю-з tg (0,7.6°) = 1,08-10 3 Н/см3;
е = 14,3 10 3 102 и---=_ 1,5288 Н/см2;
С 0,39 14,3-10-3-1022Н--7,366-JO8---—~275 Н,'см;
h -1,53 fVl,53g+41,08 iQ-3-275 m ^
2-1,08-10-8
Таким образом, необходимая глубина заложения от верха засыпки до низа трубы из условия продольной устойчивости должна быть не менее 212 cv, а высота засыпки над трубой —111 см, т. е несколько, больше, чем минимальная высота, равная по нормам 100 см.
Пример 2. Проверить устойчивость подземного участка трубопровода лиаметром 1420X10,5 мм, проложенного с отводом машинного гнутья К = 60 Dв с углом поворота 3е при рабочем (нормативном) давлении на Данном участке />=7,5 МПа и положительном температурном перепаде А<^40°С. Глубина заложения до верха трубы /г= 120 см, грунт — суглинок со следующими характеристиками: \гр = 1,43* 10-* Н/см3 фгр = 11°, Сгр= ~1 Н/см*, Сх о=0.03 М Па/см=3 Н/см3.
Определяем предельное сопротивление поперечным перемещениям трубы вверх
Площадь сечения стенок трубы F—727,5 см!, вес единицы длины трубопровода q-tj, 70,7 Н/см, изгибная жесткость трубы ?7 3,75 • 1013 П • см!.
Предельное сопротивление грунта вертикальным (вверх) перемещения! трубы определим по формуле (3 25)
<7„р гР 1,43-10-2 142^191 142^-|- 1,0 [1,43-10-*-1912 X
X
tg(0,7 ll)+-0,'-9i — j = 480
Н/см. cos(0,7 11)J
Коэффициент разгрузки по (3.27)
4ЯГ)
Ср -—-= 1,8 Н/см2.
120 + 142
Предельное Сопротивление поперечному перемещению
Ям» = <?тР + «грТпр.гр = 70,7 + 0,8 480 455 Нем.
GC 3°
Длина хорды отвода = 2р sin = 2 60- 142-sin = 4,6 м.
Очевидно, что длина полны выпучивания LKP будет больше длины хорд] кривой, т. е. в поперечных перемещениях при возможной потере устойчивости будут принимать участие и примыкающие к отводу прямолинейные участки трубопровода. Поэтому расчетный радиус начального изгиба определим методом приближении. Задаемся возможной длиной волны выпучивания L„p=50 DB~70 м. Исходя из этого, определяем расчетный pannvd по (560) Щ
2-702cos 1,5°
ро =----= 560 м
я*[70sin 1,5й —2-60-1,42(1 —cos J,5?)J
При данном расчетном радиусе определяем критическую длину волны вы-' пучивания по (5.47):
= -,
=9,6-107
см2;
5,6-10v 455fl + A/l + -E^0^8^
V V (5,6 10*-455)2 )
LKp = 9,8 ¦ 10s см = 98 м.
Принимаем длину волны, равную среднему арифметическому значению двух последующих приближении /,вр = (70+98)/2=84 м. Далее, расчет повторяем:'
2-842 cos 1,5
ро =--= 668 к,
IX2 [84 sin 1,5 — 2 60 -1,42 (1 —cos 1.5))
Llp *-ggWS^-----------
= 9,04¦ 10» сма
;
6,68- 10-M55 f I 4- л/* +
-^,7——-i'- "j
V V (6,68-10* 455)2 /
LKp = 9,5 103 см = 95 м.
Принимаем:
LKp = (84 + 95) 2 = 89,5 m,
2 89,5a cos 1,5
Po ==--— 7IV м
лг[89,5 sin 1,5 —2-60 1,42 (1—cos 1,5)]
ЬР 7,1•10*-455 '(1—f- Л + В-ЬЗ-^i)
LKp = 9,4-103 см = 94 м
Принимаем LKP=92,5 м:
п2 [92,5-sin 1,5-2-60-1,42(1 —cos 1,5)]
I*__MB-gJB-jg_____—8.7!-l(ft см*;
7.34Л0.-455 f 1 + а/,-Ь )
\ V (7,34-Ю4 455)2)
LKP = 9,33-103 см ~= 93,3 м.
Принимаем окончательно Lt:p~93 м, ро=7-40 м
Так как расчетный радиус меньше 1000 D„, то при определении эквивалентного продольного усилия учитываем влияние продольных связен и самокомпеисации системы.
Вычисляем сопротивление грунта продольным перемещениям трубы. Коэффициент, учитывающий образование свода естественного равновесия грунта, по (3.22) будет
(190\2 120
— 1 +0,367—4-0,06 = 0,34.
142) 142
Предельное Сопротивление грунта продольным перемещениям трубы по /3.20) составит
tnp = 0,8 (70,7 tg 11° + 2 -1 43 10-2 0,34-лХ X 1422tgll° + 0,6n-142-l) = 311 Н/см.
Расчетная стрелка начального изгиба по (5.49)
-0^--°:3
|l8,j_ _24,2 см.
i+^
<7пр 455
Вычисляем безразмерные параметры по (5 57) и (5.56) :
В = 9300 л /--гг— =2,75;
V 2,1 • 1C5-727,5
Д. - ¦———(24,2а 2 24,2 -118,4) = 2,03 10~« 32-9300*
Проверяем наличие участка предельного равновесия грунта при продол ных перемещениях по (5.54)
2,1-10’-727,5-2,75 2,03 104
'¦I,* ^ 1 •
311-9300
1+2/2,75
Тогда эквивалентное продольное осевое сжимающее усилие по форму (5.58) будет:
1,1-7,5138,7'
2-1,65
= 1,24 10Б МПа смг= 1,24 10’ Н;
X /i + 120,3 -10^ 2, КЯ.727,6 г_2_У - 1 L 1.05-10? Н ¦
L V 311-9300 v 2,75) J
Критическое усилие, которое может выдержать данный участок трубопр вода, по (5.48) составит
tfKp =0,375-455-74000 1,26-10’ Н.
Предельное состояние:
1,05 10’ <0,9-1,26 10»; 1.05-10* < 1,13-10»,
т. е. условие норм выполнено, продольная устойчивость обеспечена.
Пример 3. Проверить продольную устойчивость газопровода диаметром 1420x16,5 мм, проложенного в насыпи.
Угол поворота в горизонтальной плоскости, равный 14°, выполнен уп ругим изгибом р=2000 м Воздействия: температурный перепад Д^=58° внутреннее давление р=7,5МПа. Размеры насыпи: ширина по низу Ь=8 4 м, ширина по верху а=2,4 м, высота // = 2,4 м Грунт со следующими фи зико-механическимк характеристиками: \Гр 1,5 -10 2 Н/см®, <prF= IS®, сгр= =0,5 Н/см2, с* о=0,03 МПа/см=3 Н/см3.
Предельное сопротивление грунта поперечным перемещениям трубы:
<Тп. тр = <7тр tg<Prp = 70,7-tg 19° = 24,3 Н/см;
[Г
1
(а±Ь)Н
= 1,5-10-2 tg 19'
2 4
слл__ 149
_|_0,5-—--—— 653 + 174,5 = 827,5 И/см;
142 240 ^^240±840^ 240_И2Л
^пр. гр ^гр ^ Фгр
b-Dn
<?ПР гр = V^Dnfep. fep tg* ^45 + ^ + (tg 45° + ;
_„(«• + Ж ) + Tgi^_(te45»+ -f-) =.,% + 0.55 - !iH<
<7np.rp= 1.5 I0-2 170-142 2,51 =909 Н/см.
Принимаем для расчета меньшее значение qцр. гр.
Предельное сопротивление поперечным перемещениям
Qnp Qn- тр пгрУпр гр = 24,3 + 0,8-827,5 = 686 Н/см.
с SnZIE. = I 63 Н и3
6/2 840
Принимая Ро=Р, находим
расчетную длину волны выпучивания по (5.51) 4
-93.5-3,75. >0»-= 12,5 10е
см*;
2.10*.«e('l +
iKp — 3,5-103см — 35 м.
Длина хорды упругой кривой
L0 = 2р sin ~ — 2 ¦ 2000 - sin —— = 487,5 м.
Так как L0>LKP, то потеря устойчивости возможна на участке упругой кривой, поэтому принимаем р0 р-
Критическое продольное усилие по (5.52)
NKP = 0,212 686 2-105 = 2,91 105 Н.
Экпивалеитное продольное усилие
S3Kd = («А<? + 0,2акц) F — (12 10-6-58 2,1 10s -[- 0,2-346.8) 727,5 =
= 1,5710s МПа см2*= 1,57-10’Н.
Проверяем предельное состояние по продольной устойчивости: ЯэквзеягЯкр’, 1,57-107 <0,9 2,91 107, т. е. условие норм выполнено, продольная устойчивость обеспечена.
РАСЧЕТ ПОДЗЕМНЫХ ТРУБОПРОВОДОВ С ПРОИЗВОЛЬНЫМ ОЧЕРТАНИЕМ ОСИ В ВЕРТИКАЛЬНОЙ ПЛОСКОСТИ С ПРИМЕНЕНИЕМ ЭВМ
Как показа-i проведенный анализ опубликованных работ, решение для определения напряженно деформированного состояния можно получитш в замкнутом виде только для простейших расчетных схем при условных моделях грунта. Исследование устойчивости также выполняется приближен^ ными методами с введением ряда существенных допущений и гипотез. Из-| ложенные в пятой главе методы расчета на продольную устойчивость тожя выполнены с рядом упрощающих предположений и гипотез, которые в ос-": повном Идут в запас устойчивости. Так, принимается, что при выпучивании] подземного трубопровода форма изгиба соответствует бесконечной жесткости основания под трубой; взаимодействие участка выпучивания с соседнюД участками учитывается неполностью, что при наличии выпуклых и вогнутый кривых приводит к значительным запасам и т. д. Кроме того, эиергстичеЯ с кие методы исследования не позволяют достоверно оценить напряженной состояние трубопровода, так как решение существенно зависит от принятый форм выпучивания.
Сложность расчетной схемы подземного трубопровода, состоящего из-произвольного сочетания прямолинейных и криволинейных участков, разно! образие характеристик грунта по длине, существенная нелинейность системы и среды вызвали необходимость применения численных методов, которые за счет совершенствования процесса расчета и использования метода итераций^ позволяют более точно и полно, чем аналитические методы, описать взаимо-1 действие трубопровода с грунтом,
§ 1. Область применения программы «Дога»
Программа «Дога» для ЭВМ ЕС, разработанная ВНИИСТом и ЮжНИИ- ] гипрогазом [37] (программа на машинных носителях хранится в организа-, циях-разработчиках), позволяет рассчитывать подземный трубопровод про-1 нзвольного очертания в вертикальной плоскости на воздействие температурного перепада и внутреннего давления. Длина рассчитываемого участка] трубопровода зависит от конфигурации ЭВМ и конструктивной схемы трубопровода и может составлять от 1000 до 5000 м. Участок трубопровода может состоять из произвольного сочетания прямых, выпуклых и вогнутых кривых, глубина заложения трубопровода и физико-механические характеристики грунта могут быть различными по длине. Концы рассчитываемой си-i стемы могут быть жесткозащсмленньши нлн свободными. Толщины стенки] труб и отводов могут также быть различными по длине участка.
Программа «Дога» напнеана на алгоритмическом языке Фортран-IV и может использоваться для расчетов иа ЭВМ ЕС любого типа.
Алгоритм программы «Дога» использует метод конечных элементом (МКЭ), в котором исследуемый объект заменяется совокупностью дискрет! ных элементов Метод конечных элементов, в отличие от известных методов решения статически неопределимых систем, не требует выбора основной си-i стемы.
Конструкция определяется только взаимным расположением конечных элементов между собой Сущность МКЭ подробно изложена в работе [16].
В качсстпс конечного элемента принимают одномерный элемент, находящийся и среде с двусторонними продольными и поперечными связями. Криволинейные участки трубопровода заменяют совокупностью прямых, являющихся хордами данного сектора. Взаимодействие трубопровода с грунтом
описывается зависимостью сопротивления грунта от перемещения. Численные методы позволяют использовать практически любые сложные зависимости однако, как показал проведенный анализ, излишнее усложнение этих зависимостей с практической точки зрения не имеет смысла. В данной персяи программы используют идеализированные диаграммы «сопротивление грунта — перемещение», состоящие из ряда прямых Расчетные модели грунта описаны в гл. 3. В то же время используемые диаграммы учитывают не только ограниченность сопротивления грунга, но и уменьшение последнего поперечным подвижкам вверх при больших перемещениях. Физическую нелинейность грунта учитывают итерационным методом с использованием линейных решений. Переменные параметры упругости на каждом этапе расчета определяются на основе результатов вычислении предыдущего этапа. Одновременно учитывается геометрическая нелинейность (продольно-поперечный изгиб). Перемещения и усилия на каждом этапе определяют с использованием нелинейных уравнений изгиба, принимая осевое продольное усилие из решения предыдущего этапа. Так как алгоритм программы учитывает физическую нелинейность грунта, ограниченность сопротивления грунта перемещения, то можно использовать программу для расчетов трубопроводов, прокладываемых в слабых грунтах. Алгоритм программы учитывает также самокомпенсацию системы в процессе деформаций и выполняет деформационный расчет трубопровода. Поэтому дополнительная проверка трубо
провода на продольную устойчивость не требуется
С использованием данной программы па основе вариантного проектирования определяются рациональные конструктивные решения удовлетворяющие требованиям прочности и устойчивости
§ 2. Элементы матрицы податливости
Для решения поставленной задачи использован метод конечных элементов в усилиях. При получении матрицы податливости принята гипотеза что влиянием изгиба на продольные перемещения можно пренебречь и что продольное осевое усилие но длине элемента постоянно.
При расчете трубопровода на внутреннее давление и температурный
перепад в качестве его расчетной модели принимается стержень (балка) трубчатого сечения из упругого материала. Продольные деформации определяют с учетом двухосного напряженного состояния в соответствии с обобщенным законом Гука. Считают также, что трубопровод представляет собой плоскую неразветвленную систему, расположенную в вертикальной плоскости, и в процессе нагружения вся система остается плоской.
В соответствии с постановкой задачи для вычисления матрицы податливости элемента используем уравнение продольно-поперечного изгиба
где В=Е1—из гибкая жесткость трубы; S — эквивалентное продольное усилие, вызывающее нзгиб трубопровода (положительное при сжатии); й = CyDa—произведение коэффициента нормального сопротивления грунта на днаметр трубы
Решение уравнения (6.1) запишем для элемента длиной U с начальными параметрами: перемещение v0, угол поворота tfo, изгибающий момент Мц и поперечная сила Q0. Под поперечной силой здесь понимается сила, направленная перпендикулярно к не деформированной оси стержня, т е.
Q0-Bv0-Sv0. (6.2)
Уравнения прогибов, углов поворота, изгибающих моментов и поперечных сил имеют вид;
Фе = - % Tt-~^SL Т3 + Ф0Т5 -ь и0Т В В
Л'1^ = 007’3'{ —фпВТ^ — DqBTs;
= Qa^ 4 -f" M0i i — ф0ВТg v0BTв- (6.3)
Здесь и далее индекс (i), характеризующий номер элемента, опущен.
Функции Т\—Ts от безразмерной координаты %=х/1 в зависимости от
значения корней характеристического уравнения, составленного для диффе
ренциального уравнения (6.1) вычисляются по формулам:
2vivs
K + 'f) (v2shX,S cos Xjg — vt sh Я,| s!n Я,2|)
T, = -
2vjv2
v2 (3vj - л|) shX^cos^jl cos ^ —v, (3v| — vf) chX.,?sin X2|
T ? =---
2vxv2
(vi + v2) sh sin
Vl
¦v*
при S>2^Wk j. __ 8, Sin togfc — EgSin faiiS . e,E2 fef — e|)
COS <Ог? — COS C0j?
2 2 el-?2
exsinoiS —eg sin totl .
e2 — e2ei 2
e2 cos <»2? — «I cos со, ?
eI ®2
где
| / S3 | CyD, |
| 4 В2 | В |
| ! si |
CyDu |
4BS В
©x — ej; o)2 e2Z. (6.7)
=vir+V
Уравнение равновесия продольного сжатия (растяжения) для стержня с линейными упругими связями имеет вид
dx2
где
« яО,|С*
(6.9)
Решение уравнения (6.8) запишем также в виде начальных параметров, используя зависимость осевого усилия в стенках трубы от перемещения и воздействий и граничные условия:
где EF— жесткость сечения трубы на сжатие (растяжение); р.— коэффи-1 циент Пуассона материала трубы; аКц — кольцевые напряжения От внутрсЯ него давления; а — коэффициент линейного расширения материала трубы; Л/ — температурный перепад, положительный при нагревании.
Тогда уравнение продольных перемещений и продольных усилий в стек-i ках трубы будет иметь вид:
их
= «0 ch 0| +
rJia«u-F±a^EF_sh
EFn
Nx— «0?fnsh8|-f (.V0 — fwKUF-j ahlEF) ch 9? — ahtEF -|- iiomF. (6.U|
На основании полученных уравнений (6.3) и (6.11) определим матрицу Податливости отдельно для начала и конца элемента. Элементами матрицы податливости будут перемещения в соответствующей точке только от од-|. ного из единичных усилий, приложенных в начале элемента. Элементами столбца грузовых членов являются перемещения от воздействия темпера-» туры и внутреннею давления. Элементы матрицы податливости вычисляю! по формулам: при 5 < 2 VBk
Ьп = (Я, sh 2Х, + Hs sin 2Л2);
ВН.
3
f>!2 = Ап = —-— (v2Hi sh2At + ViZ/j sin2 A2);
ВН з
62a ---(ll1 sh 2л! — H2 sin 2^2);
®i!cb —--(/^2 ch sin У*? ^ sh'Ki cos Xg) i
BH3
* _ * _ 2viv2 sh sin , ,.2\.
12cb — 2Icb---n~u 1,4 + v2)>
on s
622CD
=-^V1V-2-(Hx sh cos
Xj — H2 ch X,i sin X2);
где
В — EI; A = EF; Q~nl\ ch О 1
sh 0 sh 9
(e-2 sin toj cos Ш2 — ef sin o>2 cos wi)i
6i2' 64t— —-—- (Gs sin cOj^ sin co2 -f Gt cos tox cos w2 — G4);
Q
622 =-—-(ef sin to, cos ©j e| sin to2 cos to,) ;
BG1ele3v
6JJ св = (e2sifl °>1 - ?1sin
6j2cb = - %? - (cos ®i ~cos w2);
G ч
622CB = — (ei sin <°i - 4 sin "г). (6-14>
ио1е1е4
где
Gj = 2eJe2 (1 — cos о, cos to2) — e,e2 (e® + b|) sin to, sin co2;
02 = (e2 8|) 8162',
G3 = (Ei + e2) ele2;
°4 = («I + e'2) ele2'-
<dj — er/; <o2 = e^/. (6.15)
Остальные элементы матрицы податливости равны нулю.
Элементы столбца грузовых членов вычисляют из уравнения (6.11) как перемещение от воздействия температуры и внутреннего давления
( 0 2<ткц \ f h 0/2
(6.16)
Таким образом, получены все элементы матрицы податливости и столбца
* рузовых членов, которые используют для составления уравнения равновесия системы, состоящей из дискретных элементов
§ 3. Определение усилий и перемещений
В каждом узле системы соединяются два элемента, имеющие каждый свон геометрические и физические характеристики. Типовой узел рассчитываемой системы показан на рис. 36. Обозначим номер узла /, длину элемента, предшествующего узлу, h, длину последующего элемента Л+i, угол Между элементами \i, усилия в узле Xsi-2 (момент), Xsi_i (поперечная сила), X3i (продольная сила),
Уравнение неразрывности перемещений выражает условие равенства >|улю перемещений узла от усилий в узле, нагрузок и воздействий. Для
каждого узла мы получаем систему трех уравнений, выражающих равш ство нулю угловых н линейных перемещений по ортогональным местным осЭ
a(3i—2) (3i—5)*sf-6 + a(3e-2) (3i-4)^3i- 4 + ®(3i—2) (31-3)*3*-3 +
+ “(31-2) (3i-2)*si-2+a(3i-2) (3i-l)*3i 1+а(3?-2) (30*3f + a(3i-2)(3f+I)*s(+ll + a(3i~2) (3<+2)*3^+2 + °(3i-2) (3f+3J^s^+8 = PZ<-V j
a(3i-I) (3i-5)^sf~6 + °(3i-I) (3i—4)^si—l + °(3i—I) (3(-3)*3(-3 + c(3(-l) (3i_2) X X X3l-2 + C(3i-1) (31—l)X3l-l + a(3t-l) (3i)^3i + fl(3f-l) (3t+l)*3f+l + j + a{3t-l) (3i+2)X31+2 + aX3i-l) (3i+3)X3i+S = P3i-V a(3i) (31—5)^3*—Б + "(30 (3i—4)*Si-4 + C(3i) (3?-3)*ef 8 + fl(3i) (3i-2)X3t-i +
+ С
il*Si+ Cl
(30 (3f—1) 3f—1 I (30 (30 Si
(30 (3i+l)*(3i+l) + a(30 (3i+2)^3f+2‘
*и-г x3l -г
'3i
ч\;
"Ji*/
| I*'" '1 x \ , | |
|
(l +l)cmcpn<enby' | T |
| r,< Ll+J *1 | /С У |
Рис. 36. Узлы стыковки элементов
Коэффициенты при неизвестных уравнений (6.17) определяют, пехош из принятых направлений усилий д.ш узла, с использованием матрицы п<Я датллвостн стыкуемых элементов: I
= -<5
°рг—2) (3?—4)
'12 (0 св'
ff(3i-2) (3i-b)--Й11 (0 СВ»
а(31—2) (зг—3) ¦— ®: a0i—2) (3i—Z> — ^11 (0 ¦+" ^11 (i-J-I)’
a(3i—2) (3i—1) = *12 (0 cos Vi + ^]2 (i+1)’
а(зг—2) (30 ^12 (0 Sin V{! c(3i—2) (3t+l) — “ °U (i+1) св'
a(3i—2) <3i+2) = 612 (0 CB COS V(i+I); a(3?-2) (3?+3) = ®12 (i+1) СБ sin Т(У+1):
a(3i—I) (3i—5) = — &21 (0 CB cos Vt' й(3г 1) (3{-4) ~ — ^22 (0 CB cos Vf5 C(3(—I) (3i—3) — 633 (0 CB sin Yj’»
°(3i-l) (3i—2) = ~ *21 (i) cos Vj — *2i( t+l>; a(3i-i) (3t—I) — 622 (i)cos2 Vi + 633 (i) sin2\t -f e22 (f+I); e(3H) vSO ” (*22 (() *33 (o) S*n УI COS ?*•
°(3f—1) (3i+l) = *21 (i+I)CB:
°(3i— 1) (31+2) = — ®22 (i+D cb C0S V(,'-J-l>‘
C(3i—1) (3i+3) — ^22 (f ( f) cb sin V(i-f I)’
«<30 (3i—5) = — ^21 (!) cb sin V(I °(3i) (:ii-4) = _ ^22 (i) cb sin Vi'
°(3i) (3i—3) ~ — 633 (i) CB cos Tp °(3i) (3i—2) = ^21 (i) sin TV
«во (3i—l) ~ (^22 со ~ co)sin V/ costv;
fl(3i) (30 ~ ^22 (o sin!i V» + 633 (0 cos2 Vi I" S33 (i+|); C(3i) (31+1) = ®’
°(30 (3i+2) ~ ^33 (i+l) CB s'n Vi+1; °(3i) (3i+3) — _ ^33 (i+1) cbC0SVi+v (6 -18)
При записи правых частей уравнений (6.17) учтем граничные условия по концам рассчитываемой системы. Рассмотрим два наиболее распространенных для линейной части подземного трубопровода случая: первый — выход подземного трубопровода на поверхность к компенсатору, жесткостью которою можно пренебречь; второй — примыкание к рассчитываемой системе по ^бесконечного подземного участка, при этом перемещения трубопровода равны нулю. Тогда граничные условия по концам можно учесть с помощью продольного усилия, обозначенного на левом конце Z,, а на правом Z2. Правые части уравнений (6.J7) записываются в виде:
*3>'-2 =
*31-1 = (°зр(о Н (l)) sinY{’
*V-2, -
-(аЗЖ0 + '-fjr,]- ^2(о) COS VI-(«ЗР
(I+.) + ~~ Ч>2 (о).
где функции ?i(t) и Ег(() отражают условие приложения усилий Zi н Z2 в начале (*= 1) и конце («'=&) участка н определяются выражениями:
1 при < - 1,
Ei (0
0 при i ф 1;
1 при i = k.
(1 при С = в, _
О при i Ф k.
Величины 2\ и Z2 равны соответственно нулю при свободных левом и правом концах рассчитываемой системы и соответствующему продольному усилию при «защемлении» трубопровода.
Из решения системы линейных уравнений, число которых равно утроенному произведению числа всех узлов (3ft), определяют неизвестные узловые усилия. Для определения компонентов напряженно-деформироваиного состояния по длине элемента можно использовать полученные ранее уравнения, записанные в форме начальных параметров. Для этого по полученным значениям узловых усилий определяют начальные параметры для элемента по формулам:
U0 (?) = — ^21 (1)^31—5 ~~ ®22 <0*31- 4 ®21 (о св^зг—2 Ь
+ 622(0 се (Xst-1 cos V/ + X3i sin Vi);
Фо (i) — 6II (i)*3f-6 + ^12 (0^3<-4 ~ 6I1 (I) св-^Si 2 +
+ 612 (i) cb (A'si-l “s Vl + *3i si« Vi)-'
Ml) (0 — ^3i-5;
МО
Тогда по формулам (6.3) вычисляют значения поперечных перемещен* углов поворота изгибающих моментов и поперечных сил в любом сечей* (?=*//,) элемента.
Для определения продольных перемещений н продольных усилий в чениях элемента можно также использовать уравнения (6.11), выражени: в начальных параметрах. Однако их необходимо записать с учетом гранГ ных условии по концам рассчитываемой системы
Е(0 = [ - Xs‘-s2i?i (')]
~ "¦ +
[Xsi cos
v? -
Ха1_г sin
yt
j
§ 4, Учет геометрической нелинейности системы и физической нелинейности грунта
В связи с возможными значительными перемещениями трубопровода алгоритм программы учитывает геометрическую нелинейность системы и физическую нелинейность грунта
Геометрическую нелинейность системы (продольно-поперечный изгиб) учитывали тем, что прн вычислении матрицы податливости ее составляющие определялись из уравнения продольно-поперечного изгиба (6.1), причем счи*! тали, что эквивалентное продольное усилие S, обусловливающее изгиб эле-1 мента, не зависит от перемещения. Фактически же это усилие зависит от перемещения. Поэтому на каждом этапе расчета использовали значение уси-| лия, полученного на основе определенных на предыдущем этапе расчет® перемещений
Для определения осевого усилия используется нелинейная связь между деформацией и перемещением
Nx
где Мх — растягивающее продольное усилие в степках трубы, которое связано с эквивалентным сжимающим продольным усилием зависимостью
Под Sx понимается равнодействующая усилий, действующих в сечении трубы
Пз уравнений (6.24) и (6.25) с учетом (6.26), считая усилие постоянным |10 тлинё элемента, выполнив интегрирование, находим значение эквивалентного осевого усилия для элемента
Si ~ Soo(0 - ?fi(Al'(?) + Д2 (())’ (6-27)
гяе
Sco ,i) = (a btfi + 0.2°KU(ij)F' д - “ПО" “0(0 . a V _
(6.28)
(6.29)
В программе интегрирование осуществляется численным методом по выше пенным в соответствии с формулой (6.3) значениям углов поворота centum.
Критерием сходимости итерационного процесса определения усилий ян ляется сравнение их значений, полученных на предыдущем и последующем этапах расчета.
Расчетные модели грунта, используемые в данном алгоритме, прел стапляют собой зависимости сопротивления грунта от поперечных (вертикальных) и продольных перемещений трубы.
Расчетные модели грунта и их количественные характеристики приведены в гл. 3. Эти модели представляют собой нелинейную связь между сопротивлением н перемещением, причем модель грунта при поперечных перемещениях ввиду различной мощности груита засыпки и основания является несимметричной.
Для учета физической нетнейностн грунта используют метод переменных параметров упругости, аналогичный методу упругих решений при ис-сл довании упругопластической работы металла.
На основе полученных иа предыдущем этапе расчета характерных перемещений элемента определяют секущие коэффициентов нормального и касательного сопротивлении грунта. В соответствии с принятыми моделями грунта аналитические зависимости для определения этих коэффициентов для го элемента имеют вид:
Rrv ^гр
-— при 1>ср > —!-?-;
vcp Суо при
— <?11р —
^гр
СУО
(6.30)
9пр — Я гр
9пр 'j cuoDlt )
+
Lyo
?тр
_?пр_\ . CyoDn )
D„v,
ср
^пр
лйисх0
^пр
nD„cX0
DnCyo при Dcp< —
Ч с р
—Г при JlDH I Мер |
DHcyo
О* тёг)-
D„t>Cp
: иср ’
при
<?ЧР
Lyv
р
л
Критерии сходимости процесса записаны в виде сравнения обоих зна-1 чений коэффициентов, определенных двумя последующими итерациями.
Как показали проведенные экспериментальные исследования на ЭВМ, во! всех случаях обеспечивается сходимость процесса В то же время при разЗ личных модулях деформации грунта основания и засыпки и при поиске иаТ правления малых перемещений сходимость можно обеспечить только при сравнении абсолютных величии Это связано с тем, что прп существенно^ различных жесткостях Оснований и засыпок на первоначально прямолиней| иых участках трубопровода, где малы поперечные перемещения, при итерационном процессе происходят малые колебания относительно нервоначаль-| ного положения Поэтому в версии программы, учитывающей возмржноеД существенного отличия модулей деформации грунта основания н часыпки.1 в качестве критерия сходимости процесса принято сравнение значений ncj ремещений на двух последующих этапах расчета
В заключение следует отметить, что примененный метод учета фи -шче-ской нелинейности грунта позволяет практически испо 1Ьзовать любые лиа|
• раммы «сопротиилоние грунта — перемещение»,
§ 5. Блок-схема программы расчета на ЭВМ
Рассмотрим укрупненную блок-схему расчета (рис. 37), которая позвЛ ляет описать процесс расчета подземного трубопровода с произвольным очертанием оси в вертикальной плоскости.
Блок 1. Исходной информацией являются геометрия рассчитываемой а стемы, высота засыпки над трубопроводом и все физико-механические х. рактеристики !рунта засыпки и основания, воздействия, геометрические* механические характеристики труб н отводов, а также все нормированные коэффициенты, необходимые для проверки предельных состояний трубопрш вода.
ю-
Блок 2. Здесь вычисляются все количественные показатели, характер: зующие сопротивление грунта поперечным (вертикальным) перемещениям трубы, а также коэффициент нормального сопротивлении грунта. На перво! этапе расчета он принимается равным обобщенному коэффициенту нормаль-* пого сопротивления грунта. На каждом последующем этапе расчета, исходя из перемещений, определенных на предыдущем этапе расчета, формируете^ массив секущих значений коэффициентов нормального сопротивления грунта.
Блок 3. Этот блок аналогичен второму здесь формируется массив коэд фициентов касательного сопротивления грунта
Блок 4. Эквивалентное продольное усилие, обусловливающее изгиб тр; бопровода, зависит от воздействий температурного перепада и внутЯ_ него давления и перемещений системы. На первом этапе расчета принима ется, что усилие в каждом элементе равно усилию в защем шнном трубопроводе. Исходя из полученных на предыдущем этапе расчета перемещений, иа основе приведенного ранее алгоритма, используя численное интегриро» ваиие, определяет я массив продольных усилий, характеризующий все менты системы.
Блок 5. Матрица податливости конечных элементов вычисляется иа основе зависимостей, полученных из решения уравнений равновесия. Элементу матрицы учитывают деформативность самих элементов, т. е. геометрическую нелинейность (продольно-поперечный изгиб). В связи с этим согласно ал Л ритму имеются два подблока для вычисления элементов матрицы в зависимости от соотношений жесткости трубы и грунта.
Блок 6 С использованием матрицы податливости и столбца грузовые членов в соответствии с геометрией оси рассчитываемого трубопровода формируются уравнения равновесия всех узлов системы При этом реализуют® и записанные во входной информации граничные условия по концам рас' считываемой системы.
Блок 7. Уравнения равновесия представляют собой систему линейны: алгебраических уравнений высокого порядка. Причем матрица симметричная, ситочная и малозаполненпая. Для решения системы используется специальная подпрограмма, составленная А И Дроботя учитывающая эти особенности матрицы. Подпрограмма реализует решение системы по компактной схеме Гаусса. В результате решения системы определяются внутренние узловые обобщенные усилия.
X
Б ок 8. Используя приведенные в алгоритме уравнения для определения компонентов напряженно-деформированного состояния трубопровода, опре-д< .шются значения компонентов для различных сечений по длине каждого элемента. Компонентами напряжеино-деформироваиного состояния сечения трубопровода здесь являются продольные и поперечные перемещения, углы
| 1 |
Ввод исходных данных | г |
Определение коэффициента нормального сопротивления грунта |
* | 3 |
Определение коэффициента касательного сопротивления грунта. |
||||
| * | ||||||||||
| 6 |
Формирование уравнений равновесия | - |
5 | Матрица податливости конечных элементов |
- | Ь |
Вычисление продольных усилий | |||
|
. * | ||||||||||
|
7 | Решение системы уравнений |
в |
Компоненты напряженно-деформированного состояния | - | 3 | Проверка выполнения критерия сходимости по трем нелинейностям |
Нет | |||
| 11 | Вывод |
10 | Расчет на прочность по нормам | Да. | ||||||
| на печать | ||||||||||
Рнс 37 Укрупненная блок-схема
поворота, изгибающие -моменты, поперечные и продольные усилия Эти параметры используются при определении линейных характеристик взаимодействия трубопровода с грунтом, а также величины эквивалентного продольного усилия.
Бгок 9. Этот блок проверяет сходимость итерационного процесса учета тРсх нелинейностей системы. Выход на расчет по прочности и устойчивости проводится только в том случае, если одновременно выполняются записанные условия сходимости для трех параметров нелинейности для всех элементов рассчитываемой системы
Блок 10. Здесь по определенным значениям продольных усилий и изги-озющих моментов определяются напряжения, действующие в сечениях трубопровода. Далее, в соответствии со СНиП II-45—75, вычисляются предель-но-допускаемые напряжения в зависимости от категории участка трубопро-}да и физико-механических характеристик металла труб
Блок ((. На печать выдается вся входная информация служащая для 'нтроля ввода исходных данных, все компоненты напряженно-деформиро*-
ванного состояния трубопровода, а также количественные характеристики предельных состояний. Здесь же печатаются выводы, основанные на сравнении этих величин.
§ 6. Исходные данные для расчета на ЭВМ и выходная информация
Полная длина рассчитываемого участка трубопровода может составлять примерно 5000 м при произвольном сочетании отдельных прямолинейных и криволинейных участков. С увеличенном конфигурации ЭВМ при малой изменчивости параметров по длине трубопровода полная длина рассчитываем мого участка возрастает.
Рассчитываемый участок трубопровода должен быть ограничен сечениями, для которых известны граничные условия. Программа «Дога» может, как отмечалось, реализовать два тина граничных условий. Поэтому при возможности необходимо выбирать участок, отвечающий этим граничным условиям. Например, если к ближайшему углу поворота примыкает прямолинейный участок трубопровода длиной примерно 150 диаметров трубы, то можно считать, что сечение посередине этого участка неподвижно, и запи сать признак граничных условий — «защемление». Если же углы поворота трубопровода на большой дтнне трассы примыкают близко друг к другу, то при записи граничпых условий, но отвечающих действительности, мы получим достаточно точный результат только для участков, удаленных от крайних сечений. В этом случае по длине трассы трубопровода рассчитываемые участки должны перекрывать друг друга Выбрав рассчитываемый участок трубопровода, его разбивают на отдельные конечные элементы. Узлы, где стыкуются два элемента, должны обязательно назначаться в местах изменения любого из параметров трубопровода таких, как переход прямого участка в криволинейный; изменение толщины стеики трубы, механических характеристик материала трубы, глубины заложения трубопровода и ф] зико-механических характеристик грунта.
Криволинейные участки трубопровода заменяются совокупностью ирВ мых, являющихся хордами сектора. Круговые кривые разбиваются на од! наковые по длине элементы, число которых выбирается таким, чтобы угл: между элементами не превышали 1,5°, а длины элементов не были бо.
20 диаметров трубы.
Если угол поворота круговой кривой обозначить через а, а радиус оси(Х число элементов /г, то длины элементов и углы поворота элементов, примыкающих к первоначально прямолинейным участкам, будут соответствен!®
ln 2р sin <Pi — Фп+i = - (6.32
2 п 2 я
При этом углы между элементами в два раза больше углов между при мыкающими прямолинейными участками и крайними элементами (ф„ а/я)
Для более полного учета физической и геометрической нелинейности грунта и системы прямолинейные участки трубопроводов тоже разбиваются на отдельные элементы. Так как нелинейность проявляется при большие перемещениях, то длины элементов иа этих участках должны быть меньшими. В зависимости от общей длины рассчитываемой системы можно реко мендовать принимать длины элементов, примыкающих к углам поворотг трубопровода и к месту выхода трубопровода на поверхность, равными 5—
10 диаметрам трубы, увеличивая их постепенно до длины примерно в Ю( диаметров трубы.
Узлы рекомендуется нумеровать слева направо, присваивая первый ио мер узлу, в котором стыкуется крайний элемент с последующим, в это» случае первый элемент будет иметь индекс 1, далее номера будут возра стать.
Рабочее давление продукта на данном участке и температурный пере пад определяют с учетом технологии транспорта и условий строительств!
трубопровода в соответствии с действующими нормами. По нормам также и!)'начают коэффициенты условия работ, коэффициенты перегрузки, коэффи тент безопасности по материалу и коэффициент надежности.
Физико-механические характеристики грунта определяют на основании инженерно геологических изыскании, рекомендации л о назначению ненормированных характеристик грунта приведены в гл. 3.
Сходную информацию заносят в специально разработанные формы
Первая строка содержит информацию общего плана: наименование отдела. заказа, варианта, объекта; вторая строка — число внутренних узлов (стыковок двух элементов) илн число элементов минус единица, а также граничные условия на левом (PRZ\) и на нравом (PRZ2) концах рассчитываемой системы. При защемлении трубопровода в сечении записыьастся 1, при свободном конце — О
Третья строка содержит значения следующих параметров, ро — рабочее (нормативное) давление; А/ нормативный температурный перепад, DH — наружный диаметр трубы; а—коэффициент линейного расширения материала труб; В—модуль упругости материала трубы; р— коэффициент Пуассона материала трубы; с — коэффициент, отражающий категорию участка трубопровода; т — коэффициент условий работы; k, — коэффициент безопасности по материалу; /гл — коэффициент надежностн; nv коэффи циепт перегрузки внутреннего давления; п11Р, п2гр — коэффициент перегрузки гр\нта.
Начиная с четвертой строки, построчно для каждого участка (элемента), номера которых записываются в первом столбце, заносятся параметры, переменные по длине рассчитываемой системы I — длина элемента; у — угол между элементами (данным и последующим), в градусах и долях от него (принимается Положительным, если он образован вращением продолжения предыдущего элемента к последующему по часовой стрелке); 6 — толщина стенки трубы; h — расстояние от верха трубы до уровня грунта засыпки; R ". R-j" - нормативное сопротивление, соответствующее пременноуу сопротивлению и пределу текучести материала труб; PRG — признак грунта, при глинистых грунтах записывается 1, при песчаных — 0; уТ1> — объемный вес грунта; фгр -угол внутреннего трения грунта; Сгц—сиеплсиие гpvHTa С'у.з- модуль деформации грунта засыпки; Е,г, оси — модуль деформации гранта основания; ргр — коэффициент Пуассона грунта; сх о — обобщенный коэффициент касательного сопротивления грунта; Rrp — несущая способность грунта.
Общее чис-ю элементов участков будет равно (ft+1), значение последнего уг.чг> грь+1 заносится равным нулю.
Максимальное значение величины k зависит от конфигурации ЭВ М; так, при конфигурации в 128 килобайт максима 1Ьнос значение k равно 100.
Выходная информация содержит первоначальные исходные данные. При 5т >м печатаются все необходимые комментарии. Распечатка исходных дан ных позволяет контролировать их ввод и перфорацию, а также получать го-овую техническую документацию
Далее, на печать выдастся таблица с результатами расчета (см пример). Знак плюс при значении изгибающею момента означает, что при изгибе трубопровода в вертикальной плоскости растянуты нижние волокна (Нак минус—растянуты верхние волокна тр>бы Знак плюс при значении п1'одольного осевого усилия означает, что усилие растягивающее, знак минус - сжимающее. Знак плюс при значении поперечной силы указывает иа TQ- что на левом конце элемента поперечная сила с л мигает этот конец относительно предыдущего участка вверх, а на правом конце — относительно последующего элемента вниз Знак плюс прн значении поперечного перемещения означает, что данное сечение перемещается вниз относительно элемента, минус — что это сеченпс перемещается вверх. Знак плюс при значении продольного перемещения означает, что сечение перемещается слева направо вдоль элемента от начала к его концу, знак минус указывает на противоположное направление перемещения сечения
j
Далее, на печать выдается таблица с результатами прочностного aft чета. В первой и второй графах этой таблицы, как и в предыдущей, приведен номер участка и текущая координата. Далее, в третьей, пятой и седЯ мой графах печатаются вычисленные в соответствии со С-НиП 11-45—75 на-. пряжения но оси трубы н в крайних фибрах сечения. В четвертой, шестой? восьмой графах печатаются предельные значения этих величин.
Заканчивается расчет иа ЭВМ печатью выводов, которые указывают на соответствие рассчитываемой конструкции требованиям норм по расчету на прочность и устойчивость. ,
Отметим, что прн наличии начальных напряжений, связанных с уклад) кой трубопровода, их необходимо алгебраически суммировать с напряж ииями от температуры и внутреннего давления, определенными по дайной программе
Приведем пример применения программы «Дога-3 78» при расчете по земного трубопровода, имеющего изгиб в вертикальной плоскости. Геомс рическая схема рассчитываемою участка трубопровода показана на рис. I Длины ирнмыкаюших к поворотам прямолинейных участков приняты пр
ПоВерхмость земли
s.
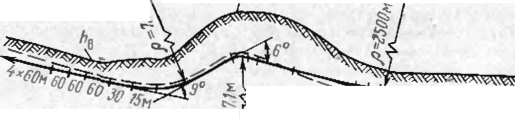
• Ось трубопровода
Рис 38. Геометрическая схема рассчитываемого участка трубопровода
мерно 500 м, для конечных точек граничные условия даны в виде «защемления» трубопровода, которые записаны в алгоритме как значения усил] по концам. Рассчитываемая система состоит из трех углов поворота, два которых выполнены с применением отводов р=5D, один — упругим изгибо! При разбивке на элементы каждый из отводов заменен двумя элементами упругая кривая — четырьмя, длины которых составляют-
для угла 9° 1П=2р sin — =2-7 1 sin 2,25°=5,57 м 2л
для угла 6° /» =2 -7,1 sin 1,5° 3,72 м
для угла 4° /„=2 • 2500 sin 0,5°=43,5 м.
Рассчитываемый участок газопроводов выполнен из труб диаметро* 1420 мм, толщииой стенки 1,75 см, за исключением отвода с углом 9°, кс| торый имеет толщину стенки 1,95 см. Рабочее давление продукта р 7,5Mnai положительпый температурный перепад Д* = 56 °С.
Для иллюстрации возможности программы некоторые из параметров приняты переменными по длине временное сопротив кине & “=570 МПа* предел текучести Лгн=470 и 420 МПа, высота засыпки над трубой fc = 100; 120, 140 см грунты песчаные и глинистые, объемный вес грунта у,р= = 17; 15 кН/м3. угол внутреннего трения фгр=19; 30°, спепление грунта сГп= = 0 012 0 003 МПа, модуль деформации груита засыпки Етр в 25; 38 МПа, то же основания Е,р осп=35, 48 МПа, коэффициент Пуассона грунта Игр —0,12; 0,22, обобщенный коэффициент касательного сопротивления грунта с,со 0 033; 0,022 МПа, несущая способность грунта /?Гр—0 15; 0,12 МПа?
Ниже приведена выходная иифермация, получаемая с ЭВМ. Она вклю:
9
чаеТ исходные данные, которые служат для контроля, результаты расчета /усилий и перемещений) и прочностной расчет. На основании полученных данных проводят анализ работы конструкции. Вначале проверяют правильность принятых граничных условий, критерием чего в данном примере должно служить равенство нулю всех компонентов перемещений по концам сс штываемон системы. Из результатов расчета следует, что поперечные [, продольные перемещения для начала первого участка и конца последнего имеют порядок не более —5, т. е. практически равны нулю. Из анализа леремещеиий можно сделать также вывод, что длины прямолинейных участков по концам рассчитываемой системы, вводимые в расчет, можно было уменьшить.
Далее, на основании результатов расчета можно построить эпюры изгибающих моментов, продольных усилий, поперечных и продольных пере мещеиий и провести анализ работы принятой конструкции Наибольшие изгибающие моменты возникают в углах поворота трубопровода, причем больший момент имеет место на участке выпуклой кривой. Перемещения трубо провода относительно небольшие и яс превышают 4 см. Обратим внимание, что за счет самокомненсации системы продольное сжимающее усилие в стейках трубы от воздействия температуры уменьшается, например, в 12-ом лтеиенте оно уменьшилось по сравнению с первым на 25 %.
Выводы, печатаемые ЭВМ, свидетельствуют о том, что принятое конструктивное решение удовлетворяет требованиям норм по предельным состояниям. На основе анализа и расчета различных вариантов можно принять наиболее рациональное решение, например, по критерию минимума земляных работ.
о Выходная информация
Отдел: Зйкяз: Вариант: Д ятя:
Расчет подземного участка трубопровода на прочность и устойчивость в вертикальной плоскости (Дога)
Исходные данные:
| Количество разбиений 27 Левый конец защемлен Правый конец защемлен Нормативное давление, МПа 7,5 Температурный перепад, °С 56 Наружный диаметр трубы, см 142 Коэффициент линейного расширения ООО 012 Модуль упругости металла, МПа 210 ООО Коэффициент, отражающий условия работы у част- 1,00 ка | Коэфс Удел[ Коэфс Коэфс Коэфс Коэфс Коэфс | жцнент Пуассона металла ,ный вес металла, к Н/м3 )ициент условия работы жциент безопасности по материалу шциент надежности шцнент перегрузки давления шциент перегрузки грунта | 0,3 78,5 0,9 1,34 1,10 1,10 0,80 | |||||
| Номер участка |
I, см | V. градусы |
в, см | h, см |
Риг МПа |
МПа | PRG | |
|
1 | 6000. | 0.0 |
1.75 | 100. |
570 | 470 | 0 | |
| 2 | 6000. | 00 | 1.75 | 100. | 570 | 470 | 0 |
|
| 3 | 6000. |
00 | 1.75 | 100. |
570 | 470 |
0 | |
| 4 | 6000. | 0.0 | 1.75 |
100. | 570 | 470 | 0 | |
| 5 |
6000. | 0.0 | 1.75 |
100. | 570 |
470 | 0 | |
| 6 | 6000. | 0.0 |
1.75 | 100. | 570 | 470 | 0 | |
| 7 | 6000. | 0.0 | 1 75 | 100. | 520 | 470 | 0 |
|
| 8 | 3000. |
0.0 | 1.75 | 120. |
570 | 470 |
0 | |
| 9 | 1500. | —2,25 | 1.75 |
120. | 570 | 470 | 0 | |
| 10 |
557. | —4.50 | 1.95 | 120. | 570 |
470 | 0 | |
|
И | 557 | —2.25 |
1.95 | 120 |
570 | 470 | 0 | |
| 12 | 1200 |
1.50 | 1.75 | 140 |
570 | 470 |
0 | |
| 13 | 372. | 1.00 | 1.75 |
140. | 570 | 470 | 0 | |
| 14 |
372 | 1.50 | 1.75 |
140. | 570 |
470 | 0 | |
| 15 | 1200. | 0.0 |
1.75 | 140. | 570 | 470 | 0 | |
| 16 | 1200. | —0.50 | 1.75 | 140. | 570 | 470 1 | 0 | |
П р о п о л ж Р и и о
| Номер участка |
1, см | У. градусы | 6, см | ft, см |
я", МПа | Я j МПа |
I НО |
| 17 |
4350 | —1.00 | 1 75 |
100. | 570 | 470 | 0 . |
| 18 |
4350. | —1.00 | 1.75 | 100. | 570 |
470 | 1 |
| 19 | 4350 | —1 00 |
1.75 | 100. | 570 |
470 | 1 |
|
20 | 4350. | ¦ 0.50 |
1.75 | 100. | 570 | 470 | 1 |
|
21 | 1000. | 0.0 |
1.75 | 100. | 570 | 470 | 1 |
|
22 | 2000. | 0.0 |
1.75 | 100. | 570 | 470 | 1 |
|
23 | 4000. | 0.0 |
1.75 | 100. | 570 | 420 | 1 |
|
24 | 6000. | 0.0 |
1.75 | 100. | 570 | 420 | 1 |
|
25 | 6000. | 0.0 |
1.75 | 100 | 570 | 420 | 1 |
|
26 | 6000 | 0.0 |
1.75 | 100. | 570 | 420 | 1 |
|
27 | 6000. | 0.0 |
1.75 | 100 | 570 | 420 | 1 |
|
28 | 6000 | 0.0 |
1.75 | 100 | 570 | 420 | 1 |
|
Номер участка | 7гр, кН м | Фгр' градусы |
сгр, МПа | ^гр. зас’ МПа | ?гр ост МПа |
М-гр | Cjj 0, МП а хм |
Rrp, МПа |
|
1 | 17 | 19. |
.012 | 25 | 35 |
.12 | 0.033 | .15 |
| 2 | 17 |
19. | .012 | 25 |
35 | .12 | 0.033 | .15 |
| 3 |
17 | 19 | .012 |
25 | 35 | .12 |
0.033 | .15 |
|
4 | 17 | 19 |
.012 | 25 | 35 |
.12 | 0.033 | .15 |
| 5 | 17 |
19. | .012 | 25 |
35 | .12 | 0.033 | .15 |
| 6 |
17 | 19 | .012 |
25 | 35 | .12 |
0.033 | .15 |
|
7 | 17 | 19 |
012 | 25 | 35 |
.12 | 0.033 | .15 |
| 8 | 17 |
19 | .012 | 25 |
35 | .12 | 0 033 |
.15 |
| 9 |
17 | 19. | .012 |
25 | 35 | .12 |
0.033 | .15 |
|
10 | 17 | 19. |
.012 | 25 | 35 |
.12 | 0.033 | .15 |
| 11 | 17 |
19 | .012 | 25 |
35 | .12 | 0.033 | .15 |
| 12 |
17 | 19 | .012 |
25 | 35 | .12 |
0.033 | .15 |
|
13 | 17 | 19 |
.012 | 25 | 35 |
.12 | 0.033 | .15 |
сгр, МПа
градусы
гр ’
+тр
'гр.ост
МПа
МПа см
*гр, МГТа
хгр
^гр.зас’ МПа
17
17
17
17
15
15
15
15
15
15
15
15
15
15
15
19.
19.
19.
19.
30.
30.
30.
30.
30.
30.
30.
30.
30.
30.
30.
.012
.012
.012
.012
003
.003
.003
.003
.003
.003
.003
.003
.003
.003
.003
25
25
25
25
38
38
38
38
38
38
38
38
38
38
38
35
35
35
35
48
48
48
48
48
48
48
48
48
48
48
.12
.12
.12
12
.22
.22
.22
.22
.22
.22
.22
.22
.22
.22
.22
0.033
0.033
0.033
о.озз
0.022
0.022
0.022
0.022
0.022
0.022
0.022
0.022
0.022
0.022
0.022
.15
.15
15
.15
.12
.12
.12
.12
.12
.12
.12
.12
.12
.12
.12
Результаты расчета
Изгибающий момент, Н-м
Продольное усилие. Н
Координаты
Поперечная сила. Н
Поперечное перемещение, см
Продольное перемещение, см
0.0 0.5 1 0 0.0 0.5 1.0 0.0 0.5
0.0
— 1354Е—12 —.2449Н—11 —.2449Е—11 0.4187Е—10 —.6634Е—09 —6634 Е—09 0.92I2E—08
¦.329Е 07 ¦-3329Е 07 ¦.3329Е 07 -.3329Е 07 ¦•3329Е—05 ¦.3329Е—05 ¦-3329Е 07 .3329Е 07
0.0
0.7948Е—14 —.8328Е—13 —.8328Е—13 0.1709Е—13 0.3446Е—10 0.3446Е—10 —-1404 Е—08
— 01404Е—19 —. 8715Е—19 0.2327Е—17 0.2327Е—17 —.5723Е—16 0.1337Е—14 0.J337E—J4
0.6894 Е—06 0.3471 Е—05 0.7584 Е-05 0.0
0.4161 Е—0Г> 0.1 ЮЗЕ—03 0.6205Е—05
—.3004Е—13 0.1657Е—04
штимпм т I ii
П о з. о л ж е ч ii р
Поперечное перемещение, см
Продольное перемещение, см
11оперечная сила Н
Изгибающий момент, Н м
Продольное усилие Н
Координаты
0.4205Е—04 0.3723Е—04 0.9379Е—04 0.2309Е—03 0.2268Е—03 0.5612Е—03 0.1386Е—02 0.1381Е—02 0.3413Е—02 0 8436Е—02 0.8430Е—02 0.2083Е—01 0.5147Е—01 0.5146Е—01 0.8990Е—01 0.1271 Е 00 0.1271Е 00 0.1594Е 0.I999E 0.1269Е 0.1699Е 0.1951Е 0.2250Е—02 0.3778Е—01 0.7353Е—01 0.94! 2 Е—02 0.5138Е -01 0.9505Е—01 0.1251Е—01 0.2639Е—01
0.6532Е—12 0.6532Е—12 —.1379Е—10 0.2833Е—09 0.2833Е—09 —.5662Е—08 0.1098Е—06 0.1098Е—06 —.2063Е—05 0.3727Е—04 0.3727Е—04 —.6406Е—03 0.1023Е—01 0.1023Е—01 —.8920Е—01 —.1389Е 00 — 1389Е 00 0.4781 Е G.I876E 0.1882Е 0.2291 Е 0.2451 Е 0.2458Е 0.2222Е CU633E 0.1634Е —.6742Е —.3150Е —.3152Е —.3640Е
0.4236Е—07 0.4236Е—07 —.1124Е—05 0.2768Е—04 0.2768Е—04 —.64 77Е—03 0.1456Е—01 0.145Е—01 —.3169Е—00 0.6698Е 01 0.6698Е .1378Е 0.2760Е 0.2760Е 0 4310Е
— .5481Е
— 5481Е —.9153Е 0.5150Е
—. 7189 Е 0.2849Е 0.6921Е —.4727Е -.07009Е 05 1.26) 8Е 06 -.3192Е ¦ .2490Е -.4938Е ¦.1988Е -.2284Е
—.3329Е 07 —.3329Е 07 —.3329Е—07 —.3328Е 05 —.3328Е—07 —.3326Е 07 —.3322Е 07 —.3322Е 07 —.3312Е 07 —.3288Е 07 —.3288Е 07 —.3227Е 07 —.3078Е 07 —.3078Е 07 —2934 Е 07 —.2708Е 07 —.2708Е 07 -.2551Е 07 —.2353 Е 07 —.2416Е 07 —.2357Е 07
— .2285Е 07 —.2293Е 07 —.2285Е 07 —.2262Е 07
— .2207Е 07
— .2180Е 07 —.2110Е 07
— .2123Е 07
— .2118Е 07
— .0936Е—07
— .9336Е—09 —.1046Е—06
0.4365Е—04 0 4365Е—04 —1725 Е—02 0.5150 Е—01 0.5150Е—01 —. 1359Е 01 0.3335Е—04 »5Е 02
— 7784Е 0.1748Е 0.1748Е 0.2750Е
—.3898Е —.3898Е —.7102Е 0.9882Е 0.9882Е 0.1329Е 0.2707Е 0.2706Е 0.1925Е 0.2128 0.218Е 0.2300Е
— 2203Е
— .2205Е
— .2688Е
1.0
00
1 0 0.0 0.5 1.0 0.0 0.5 1.0 0.0 0.5 1.0 0.0 0.5 1.0 0.0 0.5 1.0 0.0 0.5 1.0 0.0 0.5 1.0 0.0 0.5
01
03
04 04
04
05
05
04
06
05
06 06 06
03
05
05
05
06 06 06 06 06 07 07 07 07 07 07 06 07 07 07
00
01
01
01
01
01
01
01
01
00
01
01
01
00
00
00
00
00
0.
06
06
06
06
06
| Номер участка | Координаты |
Изгибающий момент. Н м |
Продольное усилие Н |
Поперечная сила Н | Поперечное перемещение, см | Продольное перемещение, см |
| 13 | 1 0 | —.3174Е 07 |
— .2109Е—07 | —-3612Е 06 |
— .3902Е 01 | 0.4035Е—01 |
| J4 | 0 0 | — 3174Е 07 | —-2108Е 07 | 0.4083Е 06 | —.3899Е 01 | — 1639Е 00 |
| 14 | 0 5 |
— .2534Е 07 | —.2151Е 07 |
0.2807Е 06 | —.3904 Е 01 |
— 1501Е 00 |
| 14 |
1.0 | — 2096Е 07 | —.2190Е 07 | 0.1566Е 06 | — 3688Е 01 | —. 1368Е 00 |
| 15 | 0.0 | —.2096Е 07 |
— .2181Е 07 | 0.5434Е 06 |
—3683Е 01 | — 2333Е 00 |
| 15 | 0.5 | 0 1903Е 06 | — .2369Е 07 | 0.1750Е 06 | — 2151Е 01 | — 1944Е 00 |
| 15 | 1.0 |
0 8625Е 06 | — .2526Е 07 |
0.6150 Е 04 | — .6700 Е 00 |
—-1618Е 00 |
| 16 |
0.0 | 0 8625Е 06 | —.2526Е 07 | 0.6150Е 04 | — 6701Е 00 | —Л618Е 00 |
| 16 | 0.5 | 0 6328Е 06 |
—.2657Е 07 | —.751ЗЕ 05 |
0.1042Е 00 | —.1346Е 00 |
| 16 | 1.0 | 0.4381 Е 06 | — 2765Е 07 | 0.1202Е 05 | 0.2989Е 00 | —.1U7E 00 |
| 17 | 0 0 |
0.4381 Е 06 | - 2765Е 07 | — .1219Е 06 | 0.2979Е 00 | —1143Е 00 |
| 17 | 0.5 | —.5204 Е 05 | — 3032 Е 07 | — .2009Е 04 | —.3571Е—01 | —.5856Е—01 |
| 17 | 1 0 | 0.5481Е 06 |
— 3167Е 07 | 0.1607Е 06 |
04111Е 00 | —-2884Е —01 |
| 19 | 0.0 | 0-6164 Е 06 | -.3251Е 07 | —. 1380Е 06 | 0 R422E 00 | —.1611 Е—01 |
| 19 | 0.5 | —•. I343E 06 | — .3276Е 07 | —.2058Е 02 | — 4147Е-01 | — 7510Е—02 |
| 19 | 1.0 | 0.6153Е 06 |
— .3285Е 07 | 0 1380 Е 06 |
0.5439Е 00 | —.1108Е 02 |
| 20 | 0.0 | 061S2E 06 | —.32S5E 07 | —. 1389Е 06 | 0.О43РЕ 00 | —J059E-01 |
| 20 | 0.5 |
— 9329Е 05 | — 3302Е 07 |
0.6950Е 04 | —.2557Е 01 |
—.5911Е—02 |
| 20 |
1.0 | 0.2601 Е 06 | —.3311Е 07 | 0.5146Е 05 | 0.1770 Е 00 | —.2965 Е—02 |
| 21 | 0.0 | 0.2601 Е 06 |
—.3311Е 07 | — 8726Е 05 |
0.1770Е 00 | —4528Е—02 |
| 21 | 0.5 | —.1633Е 05 | —.3313Е 07 | ¦—.2416Е 05 | 0.1051Е 00 |
—.3999Е—02 |
| 21 |
1.0 | — .6458Е 05 | —.3315Е 07 | 0.4177 Е 04 |
0.3149Е—01 | —.3531Е— 02 |
| 22 | 00 | - 6458Е 05 | —.3315Е 07 | 0.4178Е 04 | 0-3149Е—01 | —.352SE— 02 |
| 22 | 0 5 |
— .1928Е 05 | —3318Е 07 |
0.4066Е 04 | — 1423Е—01 |
—.2743Е-02 |
| 22 |
1 0 | 0 3677Е 04 | — .3320 Е 07 | 0.7602Е 03 | —.5036 К—02 | —.2135Е—02 |
|
23 | 00 | 0 3677Е 04 | — .3320 Е 07 | 0.7602Е 03 | — 5036Е—02 | —.2156Е—02 |
| 23 | 0 5 |
— 1741Е 03 | —.3324Е 07 |
—.4074 Е 02 | 0 2563Е—03 |
—.1311 Е—02 |
| 23 |
1.0 | 0 7188Е 01 | .—3326Е 07 | 0.2187Е 01 | —. 1322Е -04 | — 8015Е—03 |
|
24 | 0.0 | 0.8211Е 01 | — .3326Е 07 | 0 2174 Е 01 | — 1304Е—04 | — .8047Е-03 |
| 24 | 0.5 |
-.2811Е 00 | — .3327Е 07 |
0.5751 Е—07 | — .5089Е—07 |
--38I1E-03 |
| 24 |
1.0 | - 4370 Е—01 |
— .3328Е 07 | —.1953Е—01 | 0.1954Е—07 |
—-1776Е—03 |
ПрОДО .1) ж !1 И
| Номер участка | Координаты |
Изгибающий момент. Н-м |
Продольное усилие. Н |
Поперечная сила, Н |
Поперечное перемещение, см |
Продольное перемещение, см |
| 25 | 0.0 | — .5061Е—03 | —.3328Е—07 | — 1799Е—03 | 0.2064Е-00 | —. 1860Е—03 |
| 25 |
0.5 | —.5312Е—04 | — .3329Е 07 | —.8638—06 |
—.4Я23Е-10 | — .8637Е ¦—04 |
| 25 | 1.0 |
—.2972Е—05 | — 3329Е 0/ |
0.1583Е—06 | — .1566Е —13 |
—.3745Е—04 |
| 26 |
0.0 | —.2563Е—05 |
—.3329Е 07 | 0.2396Е—06 |
0.6055Е—12 | — 4349Е—04 |
| 26 | 0.5 |
0.1337Е—07 | — .3329Е 07 |
—.6839Е—08 | 0 .1506Е -13 |
—-1870Е— 04 |
| 26 |
1.0 | 0.8768Е—07 | —.3329Е 07 | — 5238Е—08 |
—.7427Е—13 | — 4833Е—05 |
| 27 | 0.0 |
0.3166Е—09 | — .3329Е 07 |
— .2558Е—10 | — 8996Е—16 |
— .1987Е—04 |
| 27 |
0.5 | —.2123Е—11 | — .3329Е 07 | 0.8605Е—12 | — .1912Е— 17 | —2999Е—05 |
| 27 | 1.0 |
—.2735Е—11 | — .3329Е 07 |
0.1421 Е—12 | 0 2206Е—17 |
0.2416Е—05 |
| 28 |
0 0 | —.3625Е—13 |
—.3329Е 07 | 0.2948Е—14 |
0.1280Е—19 | — -3624Е—05 |
| 28 | 0.5 |
0.1300Е—14 | — .3329Е 07 |
— .1827Е—15 | 0 1978Е—21 |
0.6257—06 |
| 28 | 1 0 | —.1770Е—16 | —.3329Е 07 | — 3252—17 | — .1527Е—21 | 0.2416Е— 05 |
Прочностной расчет
| Номер участка |
Координаты | апр N • | МПа |
^ст11р JVl- | МПа | а„р1. МПа | fo.ipil- | МПа |
аг,р2’ МПа |
fa„P2l | МПа |
||
| 1 | 0.0 |
0.221Е | 02 | 0.348Е | 03 | — .431 Е |
02 | 0.192Е | 03 |
—.431Е | 02 |
0.192Е | 03 |
| 1 | 0.5 | 0.221 Е |
02 | 0.348Е | 03 |
— .431Е | 02 |
0.192Е | 03 | -.431Е | 02 | 0.192Е |
03 |
| 1 | 1.0 | 0.221Е | 02 |
0.348Е | 03 | —.431Е | 02 | 0.192Е |
03 | — .431Е | 02 |
0.192Е | 03 |
|
2 | 0 0 | 0.221Е |
02 | 0.348Е | 03 | —.431Е | 02 |
0.I92E | 03 | — .431Е | 02 | 0.192Е |
03 |
| 2 | 0.5 | 0.221Е | 02 |
0.348Е | 03 | —-.431Е | 02 | 0 192Е |
03 | —.431Е | 02 |
0.192Е | 03 |
|
2 | 1 0 | 0.221Е |
02 | 0.348Е | 03 | — .431Е | 02 |
0.192Е | 03 | - 431Е | 02 | 0.192Е |
03 |
| 3 | 0 0 | 0 221Е | 02 |
0.348Е | 03 | — 431Е | 02 | 0 192Е |
03 | — 431Е | 02 |
0,192Е | 03 |
|
3 | 0.5 | 0.221Е |
02 | 0.348Е | 03 | — 43 (Е | 02 |
0 J92E | 03 | — 431Е | 02 | 0.J92E |
03 |
| 3 | 1 0 | 0 221Е | 02 |
0.348Е | 03 | —.431Е | 02 | 0 -192 Е |
03 | — .431Е | 02 |
0.192Е | 03 |
|
4 | 0 0 | 0.221 Е |
02 | 0.348Е | 03 | —.431Е | 02 | 0 192Е | 03 | — 431Е |
02 | 0 192Е | 03 |
| 4 | 0.5 |
0.221 Е | 02 | 0.348Е | 03 | — .431Е |
02 | 0 192Е | 03 |
—.431Е | 02 |
0.192Е | 03 |
| Номер участка | Коор дниаты | °пр N' | МПа | f°np ЛЛ]> | МПа |
<Jnpi, МПа | t°npi^ |
МПа | СТПР2' МПа | t°npsl’ |
МПа | ||
| 4 | 1.0 | 0.221 Е | 02 |
0.348Е | 03 | —.431Е | 02 | 0.192Е |
03 | —.431Е | 02 |
0.192Е | 03 |
|
5 | 0.0 | 0.221Е |
02 | 0.348Е | 03 | - .431Е | 02 |
0.192Е | 03 | —.431Е | 02 | 0.192Е |
03 |
| 5 | 0.5 | 0.221 Е | 02 |
0.348Е | 03 | - .431Е | 02 | 0.192Е |
03 | - 431Е | 02 |
0.192Е | 03 |
|
5 | 1.0 | 0.221 Е |
02 | 0.358Е | 03 | —.430Е | 02 |
0.192Е | 03 | —.430Е | 02 | 0.192Е |
03 |
| 6 | 0.0 | 0.221 Е | 02 |
0.348Е | 03 | — 4 ЗОЕ | 02 | 0.192Е |
03 | —.430Е | 02 |
0.192Е | 03 |
|
6 | 0 5 | 0.221Е |
02 | 0.348Е | 03 | —.429Е | 02 |
0.192Е | 03 | - 429Е | 02 | 0.192Е |
03 |
| 6 | 1.0 | 0.221Е | 02 |
0.348Е | 03 | — 426Е | 03 | 0.192Е |
03 | — .426Е | 02 |
0.192Е | 03 |
|
7 | 0.0 | 0.221 Е |
02 | 0.348Е | 03 | — 426Е | 02 |
0.192Е | 03 | — .426Е | 02 | 0.192Е |
03 |
| 7 | 0 о | 0.221Е | 02 |
0.348Е | 03 | — 418Е | 02 | 0.192Е |
03 | - .418Е | 02 |
0.192Е | 03 |
|
7 | 1.0 | 0.221 Е |
02 | 0.348Е | 03 | - 392Е | 02 |
0.192Е | 03 | - .392Е | 02 | 0.192Е |
03 |
| 8 |
0.0 | 0.221Е | 02 |
0.348Е | 03 | — .392Е | 02 | 0.I92E |
03 | —.405Е | 02 | 0.192Е | 03 |
| 8 | 0.5 | 0.221 Е | 02 | 0.348Е |
03 | -.370Е | 02 |
0.192Е | 03 | - .390Е | 02 | 0.192Е |
03 |
| 8 |
1.0 | 0.221 Е | 02 |
0.348Е | 03 |
—.295Е | 02 | 0.192Е | 03 | — 497Е |
02 | 0.192Е | 03 |
| 9 | 0 0 |
0.221Е | 02 | 0.348Е | 03 | —.295Е |
02 | 0.192Е | 03 |
— 497Е | 02 |
0.192Е | 03 |
| 9 | 0.5 | 0.221Е |
02 | 0.348Е | 03 |
— .649Е | 01 |
0.192Е | 03 | —.596Е | 02 | 0.192Е |
03 |
| 9 | 1.0 | 0.221Е | 02 |
0.348Е | 03 | 0.648Е | 01 | 0.427Е |
03 | — .675Е | 02 |
0.192 Е | 03 |
|
10 | 0.0 | 0.494Е |
01 | 0.348Е | 03 | 0.S83E | 01 |
0.427Е | 03 | - .651Е | 02 | 0.227Е |
03 |
| 10 | 0.5 | 0-494 Е | 01 |
0.348Е | 03 | 0.223Е | 03 | 0.427Е |
03 | — .772Е | 02 |
0.227Е | 03 |
|
10 | 1.0 | 0 494 Е |
01 | 0.348Е | 03 | 0.7476 | 02 |
0.427Е | 03 | .128Е |
03 | 0.227Е | 03 |
| 11 | 00 |
0 494Е | 01 | 0.348Е | 03 | 0.746Е |
02 | 0.427Е | 03 |
—.128Е | 03 |
0.227Е | 03 |
|
11 | 0.5 | 0 494Е |
01 | 0.348Е | 03 | 0.454Е | 02 |
0.427Е | 03 | —.987Е | 02 | 0.227Е |
03 |
| 11 | 1 0 | 0.494Е | 02 |
0.348Е | 03 | 0.533Е | 02 | 0.427Е |
03 | —.196Е | 03 |
0.227Е | 03 |
|
12 | 0.0 | 0.221Е |
02 | 0.348Е | 03 | 0.510Е | 02 | 0 427Е | 03 | —.108Е |
03 | 0.192Е | 03 |
| 12 | 0.5 |
0.221Е | 02 | 0.348Е | 03 | —,;96Е |
02 | 0.1926 | 03 |
—.108Е | 03 |
0.192Е | 03 |
|
12 | 1.0 | 0.221Е |
02 | 0.348Е | 03 | 0.551Е | 02 |
0.427Е | 03 | —.НОЕ | 03 | 0.192Е |
03 |
| 13 | 0.0 | 0.221Е | 02 |
0.348Е | 03 | 0.550Е | 02 | 0.427Е |
03 | —.110Е | 03 |
0.192Е | 03 |
|
13 | 0.5 | 0 221Е |
02 | 0.348Е | 03 | 0.694Е | 02 |
0.427Е | 03 | —.124Е | 03 | 0.192Е |
03 |
| 13 | 1.0 | 0 221Е | 02 |
0.348Е | 03 | 0.914Е | 02 | 0.427Е |
03 | —.146Е | 03 |
0.I92E | 03 |
|
14 | 0.0 | 0 221Е |
02 | 0.348Е | 03 | 0.915Е | 02 |
0.427Е | 03 | —.146Е | 03 | 0.192Е |
03 |
| М | 0.5 | 0.221Е | 02 |
0.348Е | 03 | 0.669Е | 02 | Q.427E |
03 | — J22E | 03 |
Q.192E | 03 |
П р О Д П ,П «ч с н н ¦¦
| Номер участка |
Координаты | стпр JV- | МПа | 1°пр лЛ> | МПа | О.Р1' МИа | МПа | о,р2. МПа | S1 р 2^ ’ | МПа | |||
| 14 | 1.0 | о.221Е |
02 | 0.348Е | 03 |
0 500Е | 02 | 0.427Е | 03 | —. 106Е |
03 | 0.192Е | 03 |
| 15 | 0.0 |
0.221Е | 02 | 0.348Е | 03 | 0.502Е |
02 | 0.427Е | 03 |
- . 106Е | 03 |
0.192Е | 03 |
|
15 | 0.5 | 0.221 Е |
02 | 0.348Е | 03 | 0.236Е | 02 |
0.192Е | 03 | —.378Е | 02 | 0.192Е |
03 |
| 15 | 1.0 | 0.221Е | 02 |
0.348Е | 03 | —.472Е | 02 | 0.192Е |
03 | — .378Е | 02 |
0.192Е | 03 |
|
16 | 0.0 | 0.221 Е |
02 | 0.348Е | 03 | —.471Е | 00 |
0.192Е | 03 | —.650Е | 02 | 0.192Е |
03 |
| 16 | 0.5 | 0.221Е | 02 |
0.348Е | 03 | —.197Е | 02 | 0.192Е |
03 | -.581Е | 02 |
0.192Е | 03 |
|
16 | 1.0 | 0.221Е |
02 | 0.348Е | 03 | -1-.194Е | 02 |
0.192Е | 03 | — .522Е | 02 | 0.192Е |
03 |
| 17 | 0.0 | 0 221Е | 02 |
0.348Е | 03 | .—194Е | 02 | 0.192Е |
03 | —.522Е | 02 |
0.192Е | 03 |
|
17 | 0.5 | 0.221Е |
02 | 0.348Е | 03 | —.373Е | 02 |
0.192Е | 03 | -.412Е | 02 | 0.192Е |
03 |
| 17 | 1.0 | 0.221 Е | 02 |
0.348Е | 03 | —.293Е | 02 | 0.192Е |
03 | —.616Е | 02 |
0.192Е | 03 |
|
18 | 00 | 0.221Е |
02 | 0.348Е | 03 | —.295Е | 02 |
0.192Е | 03 | —.616Е | 02 | 0.192Е |
03 |
| 18 | 0.5 | 0.221Е | 02 |
0.348Е | 03 | —.371Е | 02 | 0.192Е |
03 | - .464 Е | 02 |
0.192Е | 03 |
|
18 | 1.0 | 0.221 Е |
02 | 0.348Е | 03 | —.190Е | 02 |
0.192Е | 03 | —.652Е | 02 | 0.192Е |
03 |
| 19 | 0.0 | 0.221 Е | 02 |
0.348Е | 03 | —.190Е | 02 | 0 192Е |
03 | —.652Е | 02 |
0.192Е | 03 |
|
19 | 0.5 | 0.221 Е |
02 | 0.348Е | 03 | —.374Е | 02 |
0.192Е | 03 | — .475Е | 02 | 0.192Е |
03 |
| 19 | 1.0 | 0.221 Е | 02 |
0.348Е | 03 | —.195Е | 02 | 0.192Е |
03 | —.656Е | 02 |
0.192Е | 03 |
|
20 | 0.0 | 0.221Е |
02 | 0.348Е | 03 | —.1Э5Е | 02 |
0.192Е | 03 | —.656Е | 02 | 0.192Е |
03 |
| 20 | 0.5 | 0.221Е | 02 |
0.348Е | 03 | —.393Е | 02 | 0.192Е |
03 | -.463Е | 02 |
0 192Е | 03 |
|
20 | 1.0 | 0.221Е |
02 | 0 348Е | 03 | - .332Е | 02 |
0.192Е | 03 | —.526Е | 02 | 0.192Е |
03 |
| 21 | 0.0 | 0.221 Е | 02 |
0.348Е | 03 | — .332Е | 02 | 0.192Е |
03 | —.526Е | 02 |
0.192Е | 03 |
|
21 | 0.5 | 0.221 Е |
02 | 0.348Е | 03 | — .423Е | 02 |
0.192Е | 03 | —.435Е | 02 | 0.192Е |
03 |
| 21 | 1.0 | 0.221Е | 02 |
0.348Е | 03 | —.405Е | 02 | 0.192Е |
03 | — .454Е | 02 |
0.192Е | 03 |
1
Продолжение
| сЗ | со |
со | СО |
|
с | о | О |
о |
| Щ |
Ш | U3 | |
| е* | см | <м |
см |
| Л | о | СГ> | 05 |
| с: | —* | »—| | |
| о |
О | О |
О О О О
|
со | со | со |
со | со | со | со | со |
го | со | со |
со | со | со | со | со |
со |
| о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о |
| си | ил |
UJ | ил | ил | ил | ил |
W | ш | U3 |
ил | ил | ил |
ЦЛ | ил |
ш | U3 |
|
со | со | со |
со | СО | со | СО | со |
со | со | СО |
со | со | со | со | со |
со |
| со |
со | со | со |
со | со | со | со | со |
со | со | со |
со | со | СО | СО | со |
| *¦"¦* |
ж~щ | •—i | —1 |
•—* | *—< |
¦—* | •“* | •—1 | ||||||||
| о | о | О | о | о | о | о | о | о | о | о | CD | о | о | о | о | о |
|
см | (М | CN |
см | СМ | СМ | см | см |
СМ | см | см |
см | см | см | см | Сч |
см |
| о | о | О | о | о | о | о | о | о | о | о | о | о | о | о | о | о |
| W | Ш |
W | U3 | ил |
си | ил | ил | иЛ 05 | ш | ил | ил |
ш | из | щ |
ил | |
| см |
||||||||||||||||
| со | со | со |
со | со | со |
со | со | со | со | со |
со | со | со |
со | со | со |
| ¦¦=*• |
чГ | гг |
¦4J* | п* |
TJ* | тг | rh |
тГ | '¦ф |
гг* | ||||||
С
?
| со |
со | со | со | со | со |
со | со | СО |
со | со | со | со | со |
со | со | со |
со | со | со | со |
| о |
о | о | о |
о | о | о |
о | О | о |
о | о | о |
О | о | о |
о | о | о |
о | о |
| 05 Ш | из из ш ил | ш ил из | щ из | из | из из W из из ил | ил | ил | ил | ||||||||||||
| см | см | см | со | со |
со | со | со |
СО | со | со | со | со |
со | СО | со |
со | со | со | со | со |
| сг> | 05 |
05 | со | со |
со | со | со | со | со |
со | со | со |
со | со | со | со | со |
со | со | со |
| ""7 |
—? | *“? |
—“• | ¦“* | —1 |
•—* | **“» | «—* | *—* |
—* | ||||||||||
| о |
о | о | о |
о | о | о |
о | о | О |
о | о | о |
о | о | о |
о | о | о |
о | о |
| см | см | см |
см | см | см |
см | см | СМ | см | см |
см | С) |
см | см | см |
см | см | см | см | см |
| о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
| щ | W |
ил | ил | W |
из | ил | из | из | Ш |
из | из | ил |
ил | ш | ил | ил | ш |
ил | ил | ил |
| tC | СО |
о | 05 | |||||||||||||||||
| о |
см | см | см |
СО | со | со | со | со |
со | со | со |
ГО | со | со | со | со |
СО | со | со |
со |
| гг 1 |
Th 1 | rf г |
Tt I | г |
rf I | гг Г |
¦ч** 1 | ¦чг 1 |
¦гг 1 | 1 |
1 | Tt- Г | ТГ 1 | Г}- 1 | 1 | rt" 1 | -Sf 1 | rj* г | 1 |
хГ 1 |
| со |
со | со | со | со | со |
со | со | СО |
со | со | со | со | со |
со | со | со |
со | со | со | СО |
| о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о |
|
UJ | из | ил |
ил | ил | ил | из | и | ш | си | из | ш щ | ил |
ил ил ил Ш ил ил Ш | |||||||
| оО | СО | ОО |
СО | со | 00 | со | ОО |
ОО | ОО | ОО | со | СО |
GO | ОО | ОО |
ОО | 00 | 00 |
00 | 00 |
|
КР | Th |
г}4 | rf | гг | КР |
гг |
¦чз* | Tf |
гг | •чГ | ||||||||||
|
со | со | со |
со | се | со | со | со |
со | со | СО |
со | СО | СО | со | со |
со | со | со |
СО | со |
|
о | о | о |
о | о | о |
о | о" | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
| сч | см |
см | см | см |
см | см | см | см | 04 |
см | см |
сч | см | см |
см | СА |
см | см | см |
|
| о | о |
о | о | о |
о | о | о |
о | о | о |
о | О | о |
о | о | о |
о | о | о |
о |
| из | U3 | ш | из |
из | илилилилилшилил | ил | Сь |
ил ил | из из ил |
щ | ||||||||||
| 54 | см |
См | СМ | см |
см | см |
СА | см |
см | см | см |
см | см |
см | см | см |
см | см | см | |
| см | см |
См | см | см | см | см |
С-4 | см |
см | см | см |
OJ | см | см | см | см |
см | см | см |
см |
| о |
о | о | о |
о | о | о |
О | о | о |
о | о | О |
о | о | о |
о | о | о |
о | о |
cd
С
с
г
с:
2
к I
* 5
9 ~ о
О-Е с
гг cr oL
КяЛ, = 5; О
I&S
?*1
-ч!
004
к:
*RK|
? *51 *г ® Я
?•5 5 5*1
gS?
*?,&
Sogi
?ея
ь Б o?L
X д В 1
° о а. *??
— К К 1
* 5
— “Г sf
* J
2 и о ' tflS# : О о
с
о
с:
й
О <л О о lO о О lO о О LO О О гС> о о о
о © -н о о —-©О — 0©^00~-00—‘ОО—«
о л о
аГ*
о «
?}?$?*?55?со-**‘^-т*>юююсо;оог'-Г'«-Г'-ооаоос
C4(NCN<N<NiM(N(NCqOi(N<NC4(NC'i04<NW(M(MC'J
АСЧЕТ ПОДЗЕМНЫХ ТРУБОПРОВОДОВ С ПРОИЗВОЛЬНЫМ ОЧЕРТАНИЕМ ОСИ В ГОРИЗОНТАЛЬНОЙ ПЛОСКОСТИ С ПРИМЕНЕНИЕМ ЭВМ
Ось трубопровода в горизонтальной плоскости не прямолинейна. Это объясняется не только необходимостью обхода каких-либо препятствий или сооружений, по и тем, что для уменьшения нагрузок и перемещений на пр (мыкающие к трубопроводу конструкции часто применяются подземные комненсаторы-упоры различной конфигурации.
Углы поворота выполняют упругим изгибом или с помощью отводов При выполнении углов поворота с помощью отводов машинного гнутья обычно угол «набирают» из нескольких отводов с прямолинейными вставками между ними.
При воздействии температуры и внутреннего давления происходит продольно-поперечный изгиб трубопровода. При этом возникают дополнительные изгибные напряжения. Нормы проектирования магистральных трубопроводов требуют выполнения проверки деформаций таких схем прокладки, причем для оценки предельного состояния необходимо определять максимальные напряжения с учетом поперечных и продольных перемещений трубопровода.
Учитывая разнообразие конструктивных схем, геометрическую нелинейность системы, характер взаимодействии трубопровода с грунтом и невозможность получения решения для оценки напряженно-деформиронанного состояния трубопровода в замкнутом ииде, для решения задачи используют численные, методы расчета с применением ЭВМ. С помошыо разработанной программы рассчитывают систем у и проверяют выполнение предельных состояний, установленных нормами.
§ 1. Область применения программы «Шаг -лента»
Для расчета подземных трубопроводов с произвольным очертанием оси .в горизонтальной плоскости можно использовать разработанную ВНИИСТом н ЮжПИНГипрогазом программу «Шаг -лента» для ЭВМ КС любого типа [39]. Программа написана на алгоритмическом языке Фортран IV
Конструктивная схема рассчитываемого участка трубопровода может со-стоять из прямых участков, кривых, выполненных упругим изгибом, и отводов произвольного радиуса. Тонцииа стенки трубы и деталей, а также механические характеристики металла могут быть различными по длине рас-считываемого участка Tpvбопровода. По концам рассчитываемого участка можно задать произвольные граничные условия, определяющие пзаимодей ствне трубопровода с конструкциями, примыкающими к обоим концам этого участка. Граничные усилия задаются значениями податливостей (величин, обратных жесткости) примыкающей конструкции.
Данная программа предназначена для расчета подземных трубопроводе. прокладываемых готько на иеобводненных участках трассы так как она не учитывает изменение характеристик обводненного грунта и балла-стировку. Физико-механнческне характеристики грунта, глубина заложения тРУбы, рабочее давление продукта п температурный перепад могут быть различными по длине рассчитываемого участка трубопровода. Кроме того, лр чра.мма позволяет рассчитывать трубопровод при действии на пего внешних усилий, приложенных к любой точке системы. Эти усилия представляется при необходимости в ииде трех компонентой: изгибающего момента, :ог *речиоп и продольной (по отношению к осп трубопровода) силы
I Ipoi рамма реализует нелинейные модели сопротивления грунта продольным и поперечным перемещениям трубы, поэтому может быть нспользч
вана при расчете систем с большими перемещениями и для трубопровод прокладываемых в грунтах с низкой несущей способностью.
Программа позволяет рассчитывать сочетанно различных углов nqj рота в плане, ь том числе компексаторы-уноры, подземную систему с стичной компенсацией перемещений, улаженную но типу «змейки», »1 кладку со елабоизогиутыми учагткамн, параллельную прокладку, шлей! подходы с компрессорной и na-O'HOii станции и к скважинам, ирямодщД ную систему с различными воздействиями по длине, например участок тр5 бопроьода со стабилизатором у узла прнема-пуска очистных устройаИ концевой участок трубопровода с анкером-трубой и др. "¦
Для определения напряженно деформированного состояния подземнв трубопровода используется численный метол, являющийся разновидносЖ метода конечных элементов, описанного в предыдущей главе.
В качестве расчетной модели трубопровода принимается стсржД (балка) трубчатого ссчения. Для первоначально криволинейных учас трубопроводов — отводов учитывается (п соответствии со СНнП 11-45—L1 уменьшение их жесткости по сравнению с прямой грубой. Материал тру| принимается упругим, считается, что рассматриваемый участок трубоЯ вода, представляющий собой плоскую систему, в процессе нагружения | тается в той же плоскости.
При определении деформаций трубопровода учитывается двухос! напряженное состояние напорного трубопровода на основе обобщеян закона Гука.
Взаимодействие трубопровода с грунтом описывается зависимостью с4 противления грунта от перемещения. Зависимости сопротивления грунта от поперечных и продольных перемещений приняты билинейными в виде диа-1 граммы типа диаграммы Прандтля, характеризующимися соогвсгствяв предельной несущей способностью грунта п предельным сопротивлений грунта сдвигу. Расчетные модели грунта и их количественные характер^ стнки приведены в гл. 3.
Физическая нелинейность грунта учитывается итерационным методв упругих решений с помощью переменных пирометров упругости грунта. Дл| каждого этапа расчета проводится линеаризация модели грунта. Для сх] ветстпующего этана расчета используются линейные параметры, полученной на предыдущем этане.
§ 2, Матрица податливости элемента
Так как на каждом этане расчета принимается линейная модель i рунт^ то для получения матрицы податливости используются уравнения равно) сия, в которых параметры грунта не зависят от перемещения. Для каждеи элемента можио считать, что ввиду малости поперечных перемещений и лов поворота продольные перемещения от поперечных нагрузок равны нулю.} Поэтому для определения перемещений можно использовать независим»» уравнения равновесия относительно поперечных и продольных перемещения При этом для определения поперечных перемещений используется линеймЩ дифференциальное уравнение с постоянными коэффициента ми. НелинейностИ (продольно-поперечный изгиб) будем учитывать па конечном этапе расчета* как это делается при расчете стержневых рам методом сил нли перемШ тений.
Для элемента считается, что внешнее обобщенное усилие может бытИ Приложено только по его концам, внутреннее давление и температурный перепад одинаковы по длине элемента, а элемент представляет собой балкя трубчатого сечения с заглушками по концам. j
В соответствии с постановкой задачи для вычисления матрицы лодат! лнвосги и столбца нагрузки используем следующие уравнения равновесие элемента: <
г
параметр коэффициента нормального сопротивления
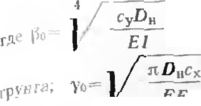
— параметр коэффициента касательного сопротивлений -р)ЯТЙ.
Здесь v — поперечное перемещение сечения на расстоянии х от начала координат; «— продольное перемещение того же сечения; cv — коэффициент локального сопротивлении грунта; D„ —наружный диаметр трубы; ?1 — ичгибная жесткость трубы; сх — коэффициент касательного сопротивления срулса; LF — жесткость трубы при сжатии (растяжении).
Используя решения этих уравнений, определяем матрицу податливости и столбец грузовых членов для элемента стержня, принимая систему коор-,з» тт. связанную с элементом. Номер элемента обозначим i. При зтом будем вычислять матрицу отдельно для начала н конца элемента. Тогда элскелгалш матрицы податливости будут перемещения п соответствующей точке только от одною из единичных усилий, а элементами столбца грузовых членов перемещения от нагрузки и воздействия при отсутствии связей но концам:
| 612 613 | |||
| дн - |
Ь-2\ 6з1 | Й2-2 б.гз 632 ^31 | — |
| Фо (Мь “1) |
Фо (<?«.¦= 1) | Фо 1W 0 — 1) | |
| ~щ(Мв = 1) | — | Ц>(Со* !) |
¦— v0 (No ~ 1) |
| ив (Мй - 1) | uo (Qo ~ Ц |
u0(N0~ 1) | |
| Vi (М«-О | ч>/№<>=-- 1) | (f <(W»=- 1) | |
| — щШ0 1) |
— »?«?• ™ 0 | — 0/ (JV. -= 1) |
|
| щ(м0~ 1) |
«HWo-1) |
||
(7.3)
(7.4)
|
».<p) | ^lPCB |
||||||
| &H/J |
- | -ов(Я) |
’ ЛкP “ | ^2PCE |
— | ||
|
6sp | «.W |
^SPCB |
«,(P> |
Злачеиия элементов матрицы податливости, вычисленные по уравнениям ' I) с использованием условий (7.3) —(7.5), будут"
6,, •= — j—— (sh 2Х |- sin
2Х);
1
¦ (ch 2Я, — cos2X);
’21
^12Cli " ^21 Си ** ---^ ^
p|?/<?
Л,21.г, — -——— (sin A ch ‘к - - co\ X sh X);
2
Siicb --(sin ^ cli X — cos К sh X);
F 1 ch 0
Oas —
‘’•пев--"Г' ГГ7Г ’
? Fy0 sh G
^18 ~ ^23 — ^31 = l%2 = 0,
где
Q — ch 2po/ -\- cos 2(50/ — 2;
Столбец грузовых членов or внешних усилии, приложенных к кои элемента, здесь не записываем, гак как эти члены вычисляются с помой матрицы податливости, приведенной выше. Перемещение от возденет^ температуры и внутреннего давления с учетом двухосного напряженного стояния грубы составит
д д _ аМ + (\ — 2{г)аки/Е ft
зр зрев ТТ" 1ПО-
cYo
При записи выражения (7.7), чтобы учесть соединение элементов Я углом друг к другу, условно принято, что каждый элемент имеет по кГ нам заглушки. Здесь номер i-ro элемента опущен; а — коэффициент лине ною расширения материала труб; At — температурный перепад, положит^ иый при нагревании; р — коэффициент Пуассона материала труб; Е — мо Дуль упругости материала труб; сгкц — кольцевые напряжения от впутрШ него давлении
§ 3 Уравнение неразрывности перемещений узла
В узле системы соединяются два линейных элемента, имеющие кажя свои геометрические и физические характеристики ирн различных воздсйсЩ виях. Кроме того, к узлу в общем случае могут быть приложены внениГ обобщенные усилия. Типовой узел рассчитываемой системы аналогичен пн веденному на рис. 36 Обозначим номер у !Ла i, длину элемента, предше^ вующеги узлу, Л, последующего — Л+i, угол между элементами <р,, узлсГ усилия X с еоотватствующим индексом, внешнее усилие в узле Z с соотвёИ ствующим индексом. ¦j
Под углом фа между элементами понимается угол, образованный вря щениеу продолжения предыдущего элемента U до совмещения с последую! щим элементом 11+>, причем угол считается положительным, если вращсиЯ осуществляется но часовой стрелке.
Положительные направления усилий в узле X и внешних усилий Z coej падают и показаны на рис. 36 н 39, причем для узла г усилия Л'-, (_2, AW*
x3i обозначают соответственно изгибающий момент, поперечную и продол ь-М
ную силы по отношению к началу каждого элемента.
г
О oCijai свойством будут обладать только крайние узлы. Так как но L. 1 Левого узла принят равным единице, го счет длин элементов начина fjcfl со второго. Крайние узлы (с индексом н начальный, с индексом к — ан<чяын) состоят из одного элемента и трех упругих связен: угловой и !|Ву\ линейных, ориентированных по этому элементу и характеризуемых сопутствующими податливостями с1и, Сгн, езн и С1в, с2к, сзк.
Уравнение неразрывности перемещеикй выражает условие равенства hv.ih: перемещений от узловых усилий и всех нагрузок и воздействий. Для каждого узла мы получаем систему трех уравнений, выражающих равенство ц\.1Ю угловых и линейных перемещении по ортогональным местным осям, которая совпадает с <6.17).
Однако в данном случае уравнении (6.17) составляют для всех системы, включая первый и последний
Порядок получаемой системы уравнений равен 3(6+2), где k— число внутренних узлов системы.
Кроме того, учитывая особенности ьраЛнпх узлов, прп формировании системы уравнений принимают условие, что неизвестное с индексом чемее единицы или более 3(&+2) равно нулю.
Коэффициенты при неизвестных (матрица податливости узла) определяются. исходя из принятых обозначений узла на основе матрицы податливости элементов, it вычигля юте я по формулам:
J(3t 2) (3i—5)
узлов
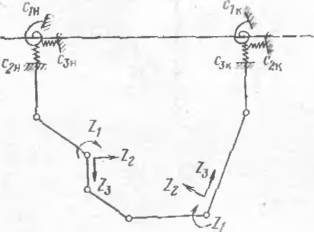
Pit с. иих
39. Ориентация связей и пнеш-уси.тий — момента и двух составляющих сил
4Р,
е (0 •
''(31-21 (31-4)
Р4(0;
Pi
°(3i-2) (3i—3) “
2Pi (?) Ь 2Р1 ((+1) + с1н ПР» •=" 1:
2р, (1) + 2р,((+1) при 1 < i < fe + 2; 2Pi (i> -L 2Pi (i+D + c1k "Pa * *= * -I 2:
3(3i—2) (3i—S)
¦P2(i+I);
a(3i-2) (31—1)
Pf
1 < 1
P2(i) C0S <Pi +
Pi
H(:ti-2) (30 P2 (i) s,n W'
a(3i—2) (3i+l) ~ — 4P6(i+l);
4
P4(?+I) cos(Pi+l;
(3i—2) (34'2) a(3i 2) (3i+3)
(7.8)
P<(i+I) sin 4><+l •
Pi+I
2fi i
2 Рз (0 COS* ф( + Sin2 4;( + _J__ p3;(+1) + e^;
1
sin»«p, + — Рза+1) |
Pj-H ¦
при J <<<?+¦
- P3 (0 cos* Ф, +
При / =*¦
Д-Рз (i) cos* Ф,. + -MjiL si,,2 4;. f _J_ p fj
P, Vi 4 ~J
y(+l
при { fc f ¦
p?
P?
Vi 2№i (0
<+»
1
I
Vi
*lt
I
«(3i~.) (30 = — sm 2q>j
_1
P?
,2 Рз<0
"ft404-1)'
aW~ 1) (3.+2) - —-Pgfi+li t'os(P/+j'.
Pi+I
V~f) <3/+3)---——P5(I+I) sinspf+,
P?
2Р<^г (о Vi
-p4C?)sin фг;
p5 <f) sin <p,;
P/+J 4
cos <pf.
°(30 (3/-2)--Г~ fW sin Ф/.
P
Pi+l
(7 9)t
fl(3i) (3i—5)
Pi
2
Q<1.) (3 —I)
“(3i) <3i-3)
't’l(i) 2 P.!(i)
'¦ft
sin 2<pi
т
“РЛ’ИО 2 I . , 2р ф ,
-cos2 Ф? + — Рз (0 мп* ф, ь —±—iii. + сан
ь Ц Т,+,
при j — 1;
V.+ l
При I < i < k 1-2;
Шт
Yi
cos*qi(+ ~p3(|)5!п*ф( f
Pf
1 - о ^Р»'+Л(1+1)
2P>^(0 C0S* »jtj + — P3(i) sin* Ф?
Pi Vi+1
+ C.
3k
при i = k-1- 2;
a(M) (3i+D ~ ®;
2Pi+A(i+l) .
°(3i) (3i+2) =- ' s,n V't-hl'
V/+J
2Pi
(7.10)
cos ф/+1.
H30 (3?+3>
Vi
i+г
Столбец свободных членов (столбец нагрузки) для узла вычисляется от действия внешних усилий Z, воздействия внутреннего давления р и температурного перепада Л< аналогичным образом
4
^3i—2 — 4Рб (i)Z 1 (i—I) ~ ~Z f’4 (1)^2 (?—1) [2Pl (i)f 1 p) "
Pf
+ 2Pl (.+1)^2 (l,IZl <i) + [ - JpP2 (() cos «P|?1 (0 +
+ P2 (i-f 1) E2I*)] Z2 (/) + p2 (0sin Z3 (0 "
Pi-f-l J "i
4
~ 4Рб (i+nE3 1 (i+l) ” P* (‘+1) C0S 'Pi+l'^S W Z2 (i+l) —¦
(7 11)
1гй»со!фа,« +
*k-x ~
cos <р(Ег (i) ----p2 a+UE-i (0
[-TTPa<‘)C
(0 +
P(i+1)
“^)--7(>3(о1?1«22(?)
-f — sin2tp-2
I VMi)cos4-+-p-P3(0sini,^?i{i) “
-b V, (1+.)?2«I (i) - ^2 ,i+.> Sin ф?+1 ?, (i) Z2 (i+1) _ I
1,1 Q '2р0ЕГ ’
ch 2ft0I — cos 2p0f г .
Ра Q ’2(5„?/ ’
г
ch Р,)/ sin Pul — sh po Icos flnf r2 Q 2 %E1
ch ft,,/ sin p,,/ -j- sh Cos Pi,/ I
Q "щГ’
Q ch 2p0I -f- cos 2p0I -— 2;
VnDncx . v Yo'"'.
F.F '
P P./;
Ps
CyD* 4 El
Po
Го =•-
chO 1
1
o-vo/; Ti -
V,
(7 14)
sh 0 2f>EF
sh 0 2%EF
S •— — аЛ( ~ (I — 2ft)
Окц ,
(7.15)
Окц —
2EF
Кроме того, в программе вычисляются площадь сечения, момент инерции, радиус инерции н момент сопротивления сечения трубы по заданному наружному диаметру и толщине стенки трубы. Для отводов учитывается уменьшение их жесткости по сравнению с прямой трубой по формулам СНиП 11-45—75
F =
4&рк
при 53:0,3;
10 1- 12^
Хк/1.65 при X* < 0,3;
1 — - ¦ ' ---fc)Ki
64
21
(7.16)
Г -
D н?я
Для простейших расчетных схем при неучете физической нелинейности Фунта можно получить решение с использованием обычных вычислительных средств. Для этого необходимо сформировать систему уравнений.
При формировании системы уравнений необходимо учитывать особенности двух крайних узлов системы, поэтому дополнительна в программе
<Pf
О при i ф k -f 2; при i=k + 2;
-{-t
?» (О
при i ф k+ 2; при f = k + 2;
f 0 при i =jfe /г+ 1; ¦
( -1 при i-bi I 'fl
§ 4. Компоненты напряженно-деформированного состояния трубопровода
Из решения системы линейных уравнений, порядок которой равен утро-1 снпому числу всех узлов 3 (6+2), определяют неизвестные условия вс всех Л узлах. Далее, используя решение уравнений равновесия (7.1) и (7.2), выадс- I ляют продольные перемещения, осевые продольные усилия в стенках трубы,* поперечные перемещения, изгибающий момент и поперечную силу. Приведем] уравнения, описывающие изменение этих параметров по длине (%=х}Ц) эле- < мента:
^tri С nt ch G,- — 1
Ni - 4 (i-n) + [(X, (i_„ - Z2 (qEj (/)) sin «Р, + i
, „ ___Sh6?g c DP sh6f(I —1) + sh6<|
+ (x3i - z3 uA <‘>) «>s — - SiEFi--
4 = .
¦-* -r (eP ^ Uo sin p0J? +
B0 cos p0/|)
+ e-W« (Co sin + D0 cos 0Л) + eW “-«> [Л L sin p^l g) -f + cos p0/ (1 - |)j + e~0' »-*> [Cx sin p0 / (i-|) + D, cos Р/ (I -1)1);
г
t ^Jl(DQ sinPoJfc- C0 cos Р(Д) + ew 1 [Л, cospb/ (1 ?)
- Bx sin p0 / (1 - ?)) + e-W (1'E) [Dj sin pe/(i _y _
— Сд cos p0/(l — I)],1; rE= —fe leW?[(^o-Bo)cosp0^-M,J +
e„) sin po/5] + e-P»'E l(Cg - D0) sin pvll + (D0 +
+ C0)cos РД + <J-S> [(/?, Ч 5,) sin р0/ (1 -1) -+ (Bt -
- Аг) cos р0/ (1 - m 4 e-Pl/ <'-«> [(D, sin (ty (I — |j —
-(Cx D1)cospoMl 1)]). (7.19)
Вспомогательные величины в уравнениях (7.19) определяют по фор
мулам:
jVoo = — aAt + f«W
(*3(—5 ~Z\ (i—1)) ^1 " р" (*3i-4 ' Z2 <?—1)) ^5'
B0 ~ (*3i —5 -^l (?-1)) l*-2 “f у (^si-4 Z4 (*—1)) ^6'
C0 = (X3i—S ~~Z\ (i—1)) ^8 n (X3i-4 ~ Z2 (/—))) ^
Pi
(*3<—5 2 1 (t—1)) 1*4 + ~7T~ (^3i—4 ~ Z2 (i—l)) IV,
Pi
^1 = (X3i~2 ~Zl (i)E 1 (0) 1*1 Г"Ц^З( —
Pi
- гз (0еi Щ sif> <p- ('v3f—I -z2(i|?i (0) cos ф] n6;
^1 = (^3C—2 ^1 (?)^1 (0) Иг + “ К*3? ' Z3 (i)^l (*)) sin 'Pi ¦
Р/
(X3?-l - Z2 (i)El W) COS ф;] Цв;
C1 — (^3i—2 ^1 (i)^l {*)) Из--r— f(^3i *3 <1)^1 (0)sin (Pi —
Pi
- (X3i_, - Z2 m) ?1 (r))cos <p,.J (/5,
D1 ~ (*3i—2 — 21 (i)?l (*)) 1*4 + у l(*3i
- Z3 (0^1 W) Sin Ф, - (Xzi_t - z.2 m?t (/)) cos 9,1 H7;
}, 2Р„* cos 2{у _ sjn 2J8,J — 2;
fi-2 = е—2Р°г — cos 2/50/ — sin 2{5(|/;
Из = — е2М_ cos 2Д(/ — sin 2Qol + 2; 1*4 — е2^'/— cos 2poi -( sin 2(5^;
ц5 — 2 sinzp0/r;
|ie — ( — e~2p°' — sin 2p„J + 1) r;
.2P«I
(7 20)
sin2fy — l)r.
Как отмечалось, физическая нелниейчость грунта учитывается по методу* упругих решений. ¦
На первом этапе расчета принимаются линейные характеристики перв^Н ветви диаграммы сопротивление грунта — перемещение:
с* с*о; С«-СУ0.
На основании определенных на предыдущем этапе расчета перемещений 1 определяют новые значения упругих характеристик для г-го элемента: Н
пр
при I нср \ >
лОц | Uqр I
Сх о При i Нср |
"ср ~ « a 0,5); ^?гр
ЯИцСх о ^пр . л?)цсх Q
('22*
пелся —
Дг
при I fep I >
vcp I
'у 110СЛ
'Гр .
Су о при I уср I «ср = »(6 == 0,5).
(7.23)
Количественные параметры диаграммы «Сопротивление грунта — перемеш щение» (с* о — обобщенный коэффициент касательного сопротивления грунта; ] ^пр — предельное сопротивление грунта продольным перемещениям трубыШ су о — обобщенный коэффициент нормального сопротивления грунта; RrV —-1 несущая способность грунта) задаются и вычисляются в программе в соотв ветствии с расчетными зависимостями, приведенными в гл. 3.
Критерием сходимости итерационного процесса является сравнение двухЯ последующих величии с* н cv. В программе это записано в видс: \
Сх поел
Су Поел су Су поел
(7.24)
0,1;
0.1.
Сх поел
Условие (7.24) должно выполняться для всех элементов рассчитываемой системы.
Геометрическую нелинейность (продольно поперечный изгиб) учитывают следующим образом. На основании расчета в линейной постановке опреде- ! ляют изгибающий момент и продольное осевое усилие. Для определения деформационного момента используют зависимость, полученную из рассмот*
(Я -(вух случаев нагрузки бесконечной балки на упругом основании: при Рсйствйи только поперечной силы н при совместном действии лопсречнон
'^продольной сил.
Из сравнения полученных решении находим, что
Л^деф = —. -
— (7-25)
\ 1 ^экв “^кр
Отмстим, что формула (7.25) отличается от аналогичной, используемой при расчетах рам, знаменателем, который имеет степень не 1, а '/а, что отражает влияние упругих связей.
Б формуле (7.25) М — изгибающий момент без продольно-поперечного изгиба: 5^,,в—эквивалентное продольное усилие в сечении трубы, вызывающее изгиб (положительное пр)! растяжении); SKp — критическая сила для бесконечного стержня на упругом основании.
Значения SKp и вычисляют на основании определенного расчетом коэффициента нормального сопротиглеиия грунта су и усилия в стейках тоубы по формулам:
?кр EDHcyn (Dl - Dl) ; (7.26)
S3KB -- Л' -0,5amF. (7.27)
Кольцевые и продольные напряжения в стенках трубопровода от нормативных нагрузок и воздействий определяют по методике, принятой в СНиП II-45—75:
Н _ Ро^вн . /у 90\
—*Г' (7 8)
<|р12 -3- ± J-^1-
тк. (7.29)
пр р JJ7
Коэффициент концентрации гп„ учитывает концентрацию продольных напряжений в отвойах н записан в программе в соответствии со СНиП 11-45—75
при Хи < 0,3;
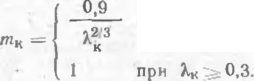
(7.30)
При оценке напряженного состояния трубопровода программой не учитываются начальные напряжения в трубопроводе, возникающие в процессе его укладки. При упругом изгибе трубопровода по заданной кривой ра плса (I изгибающий помет определяют но формуле
/Ир= (7 31)
Р
В соответствии с принятыми здесь направлениями осей координат и усилий знак плюс принимается для вогнутых кривых (при отрицательном угле поворота осн трубопровода), знак минус — для выпуклых (при положительном угле поворота) Полученное по формуле (7.31) значение изгибающего Момента алгебраически складывается со значением изгибающего момента (деформационного) соответствующего участка, выдаваемого на печать.
§ 5. Блок-схема программы расчета иа ЭВМ

В программе реализована проверка предельного состояния трубопрьв
согласно п. 8.21 СНиП 11-45 75 Предельные состояния при расчет! нормативные нагрузки н воздействия записаны в виде:
Блок-схема расчета подземного трубопровода с произвольным о1
![]()
кием оси в горизонтальной плоскости приведена на рис. 40. Опишем блокам. Я
Блок 1. Исходной информацией япляются значения усилий и воздействии
по длине рассчитываемого участка, геометрий рассчитываемой конструкцией фнзико-мехаиическис характеристики трубы и грунта. В этом блоке выч«цЯ ляются параметры, характеризующие жесткость элементов трубопровода, расЯ четные параметры моделей грунта, а также другие характеристики, не зав^| сящие от итераций. «
Блок 2 Матрица податливости вычисляется для всех элементоп рассч^Н тываемой конструкции, т. е. для значения г, изменяющегося от 2 до fe+2.4 Вычисления проводят по ранее приведенным формулам, принимая иа иулеВ^Н итерации значения упругих характеристик грунта рапными начальным.
Блок 3. Здесь вычисляется столбец свободных членов уравнения неразв рывности перемещений в зависимости от значений узловых внешних усилив и воздействия температуры и внутреннего давления.
Блок 4. Система уравнений формируется в соответствии с задапньн^^И уравнениями с учетом граничных условий. Матрица системы получается леи-® точной и симметричной. Для решения системы линейных уравнений высоког^И порядка используется специально разработанная подпрограмма. В резуль-И тате решения системы уравнений определяют неизвестные внутренние узловЫ^И усилия. в
Блок 5. Используя зависимость перемещений от узловых усилий, записан-» ных ранее, определяют характерные перемещения—поперечные и продоль-Я ные перемещения середины (1=0,5) каждого элемента. ¦
Блок 6. По характерным перемещениям, используя метод упругих peine-Я кий, по диаграммам «сопротивление грунта — перемещение» формируют ио- Ж вые массивы упругих характеристик грунта. ]
^ Критерием сходимости процесса прн определении фактических „«иных характеристик нелинейной модели грунта является сравнение велн-ч'ч' ,lii др^х послелуютнх итерациях. Если установленные критерии для №х элементов не удовлетворяются, то вновь сформированные массивы уп-вх1)1ч характеристик грунта засылаются в блоки 2 н 3. Далее, весь процесс расчета повторяется. При З'довлетвореннн критериев сходимости переходят к блоку 8.
Блок 8. На основе найденных окончательных значений внутренних узло-вь,х усилий определяются все компоненты напряженно-деформированного состоянии. трубопровода, деформационный изгибающий момент и усилия, действующие на примыкающую к рассчитываемой системе конструкцию.
Б-юк 9. Определяются кольцевые и продольные напряжения в трех сечс-(И1ЯХ трубопровода (в начале, середине и конце элемента). Прп этом учиты-

Рис. 40. Блок-схема программы «Шаг — лента»
кается концентрация кольцевых и продольных напряжений для кривых труб (гтводов). В соответствии с предельными состояниями, установленными нормами, определяются предельные кольцевые и продольные напряжения в сжатий н растянутой зонах сечения.
Блок 10. На печать в табличной форме с необходимыми комментариями выдаются значения перемещений, усилий и напряжений в сечении трубы, нагрузок иа крайние связи, предельных напряжений, установленных нормами. Кроме того, проводится сравнение действующих и предельных напряжений 1' делается вывод о выполнении условий предельного состояния. При невыполнении условий указывается участок, где условие не выполняется.
§ 6. Подготовка исходных данных для расчета на ЭВМ
Вначале вся рассчитываемая система, состоящая из прямолинейных и криволинейных участков трубопровода, разбиваетси на отдельные конечные Элементы. Узлы, где стыкуются два элемента, должны обязательно иазиа->агься п местах изменения любого из параметров трубопровода: давления
1 Родукта, температурного перепада, диаметра и толщины стенки трубы, гзико-механических характеристик трубы и грунта, приложения внешних Ус илий, а также стыка прямой с кривой.
Криволинейные участки трубопровода заменяются совокупностью мых, являющихся хордами сектора. Рекомендуется па основании числешЗ экспериментов число элементов, на которое разбивается криволинейный сток, выбирать таким образом, чтобы углы между элементам» не превыщД 10°. а длины элементов были бы равны примерно 5—20 диаметрам тпД в зависимости от радиуса изгиба, принимая большую длину элемента jH участков кривых, выполненных упругим изгибом.
Кривые малого радиуса (отводы) рекомендуется разбивать на одинаЛ выс по длине элементы Длину каждого из участков, на которые разб J ется криволинейная вставка, определяют по формуле
«1
2n
In =* 2pisln
Углы поворота стержней, примыкающих к первоначально нрямолия ним участкам, получают по формуле
«I
2п
(7.371
а углы поворота остальных участков — по формуле
(7.:
ЧРв = Т,— ¦ —ф„- —•
В формулах (7.36) — (7.38) приняты следующие обозначения, р,—радпЯ оси изгиба упругой кривой или отвода, см, U| — угол поворота упругой кр| вой или отвода, градусы; п — число элементов, вписанных в данный
Прямолинейные участки трубопроводов также разбивают на отделън! элем emu Это делается для того, чтобы более полно учесть физическую {¦ геометрическую нелинейности грунта и системы. Поэтому на участках, где' могут иметь место большие перемещения, длины элементов должны быть! меньшими. Можно использовать в местах примыкания к углу поворота эле-1 менты длиной примерно п 5- (0 диаметров трубы, увеличивая их постепен^И до длины в 100 диаметров трлбы. Углы поворота между этими элементами! равны нулю. Радиус кривизны такого участка принимается р=0,Ы021. 1
Далее, определяют граничные условия рассчитываемою участка трубой провода, которые характеризуются податливостями упругих связей: углов вой С|, поперечной с2 и продольной сз. J
Ясли к углу поворота примыкает длинный прямолинейный участок труш бопровода, то на определенном расстоянии от него .можно считать трубоД провод защемленным. Тогда податливости этой точки будут равны нулю! (ci=0, Сг=0, с3=0) и ее можно принять за крайнюю точку рассчитываемой системы. Длина прямолинейного участка, па котором происходит перемещав пие трубопровода, зависит от угла поворота и физико механических харакШ герисгик грунта. Ориентировочно длину этого участка можно принять рав® ной 500 диаметрам трубы. Контролем правильности выбора длины этого* участка служат значения усилий в начальной точке, получаемые на осиоваД пин расчета, которые должны соответствовать усилию в затомленной части I трубопровода. Введение в расчет более длинных, чем необходимо, чзстков 4 не изменит результатов расчета, но увеличит время счета на ЭВМ. В то жеЯ время следует учитывать, что максимальное число элементов, иа котороеШ разбивается данная система, зависит от мощности ЭВМ и для ЕС 1020 ] не должно превышать 121. 1
При отсутствии связи по какому-нибудь направлению податливость ее I равна бесконечности (принимаемое в расчете значение 0,1-1051). Если рас- 1 считываемый подземный участок трубопровода примыкает к открытому над- 1
„ому переходу с компенсатором, то, пренебрегая жесткостью последнего,
3 О принять податливости для этой точки равными бесконечности.
' Для любой упругой конструкции, примыкающей к рассчитываемому уча-с трубопровода, ее податливость определяется по общим правилам строите Luofi механики.
Если рассчитываемый участок трубопровода соединяется тройниковым соединением с прямолинейным полу бесконечным в обе стороны от лодсоеди-„сиия трубопроводом (рис. 41), т0 соответствующие податливости, т е. перемещения от единичных усилий, определяются по форму лам:
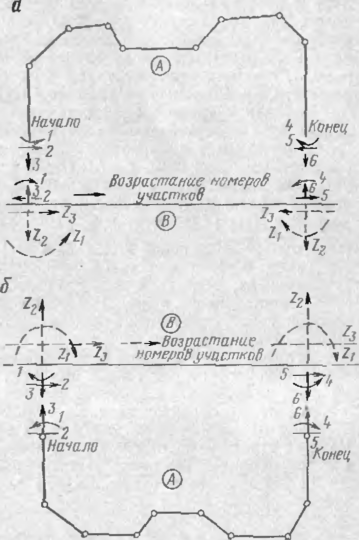
Рис. -41 Положительные направления усилий при примыкании рассчитываемой конструкции к магистрали: а — конструкция примыкает снизу; б —конструкции примыкает сверху
Cl =•
t3-=—i—. (7.39)
3 2 EFy„
Величины ixm, Рм и \-м вычисляется по формулам:
SM
4 El
4 EI
S„ =(ctAf? + 0,l
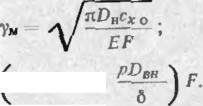
(7.40)
Здесь все параметры трубы, грунта и воздействий относятся к основной магистрали, к которой примыкает рассчитываемый уча-с ок, и имеют следующие обозиа-41 пия:
Ь — модуль упругости материала трубы; F — площадь сечения стснок трубы; I — момент инерции сечення стенок трубы; D,, — наружный диаметр грубы; DBn — внутренний диаметр трубы; 6—толщина стенки трубы; Сх ч—обобщенный коэффициент касательного сопротивления грунта; с„ 0 — обобщенный коэффициент нормального сопротивления грунта; а — коэффициент линейного расширения материала трубы; At — температурный перепад, г |'ложительпый при нагревании; р — нормативное значение внутреннего дав-•тення продукта.
Узлы рассчитываемой системы нумеруют по порядку слева направо, при свайная первый номер левому крайнему узлу. Тогда элемент между первым и вторым узлом (первый участок) будет иметь индекс 2 Далее номера участков будут возрастать.
Положительные направления внешних усилий Действующих в горизои тальной плоскости: момента Zmy, поперечной силы Zsiiy и продольной силы
Zs(fj — приведены иа рис. 41. Им присваивается индекс номера узла, гдЛ действуют эти усилия.
Физико-механические характеристики грунта характеризуются в осноЛ ном нормированными показателями. Рекомендации по их определению изло-5 жены в гл. 3. j
Входная информация заносится в специально разработанные формыЯ Первая строка содержит информацию общего плана—наименования отдел* (8 символов), заказа (4 символа), варианта (8 символов), даты (8 сим о-лов) и объекта (52 символа). В скобках указано максимальное число сщВ волов. Во вторую строку заносятся значения параметров, которые постоянная но длине рассчитываемого участка; k — число внутренних узлов (стыковка двух элементов) или число элементов минус единица; а, ?, ц (для стали • р<=0,3), а — расстояние от трубы до стеики траншеи, k„ — коэффициент на-1 дежиостн, принимаемый по табл. 10 СНиП II-45—75
Начиная с третьей строки, построчно для каждого участка (элемента* заносятся все характеристики в следующем порядке. Первая вертикальней графа показывает номер участка, причем счет участков начинается со втуЩ рого. Далее — величины: Ро, At, DB, 8, I, ср, p — радиус оси изгиба трубопроМ вода для элементов, принадлежащих к прямолинейному трубопроводу, при-] иимается равным бесконечности (вводится величина 0,1-10s1); с (прин мае- h мый по СНиП И-45—75), h, Xrp,R!J ; тип грунта (вводится ноль для песча | ных грунтов и единица для глинистых); угр. фгр. Сгр, Етр, Цгр, Сх о, RTp. i Таким образом заносится информация для всех элементов (участкся^в трубопровода, последний номер которого равен k+\. Значение последнегЛ угла поворота равно нулю. Далее, заполняется вторая форма, первая сторт^В которой содержит значения податливостей связей в начале и конце рассчнЯ тываемой конструкции: 1
С|—угловой, с2 — поперечной; Сз — продольной. ¦
Начиная со второй строки для всех узлов, номера которых от единицы j до /г+2, записываются значения внешних узловых усилий: Z\—изгнбаюпцЯ момент, — поперечная сила, Ъъ—продольная сила. Ш
Подготовка исходных данных для расчета выполняется на перфокартах. Каждая строка — на отдельной перфокарте. Первая строка содержит текстовую информацию, все последующие — цифровую.
Порядок набивки такой: сначала все заполненные строки первой формы, затем — второй.
Для контроля заданных исходных данных и правильности перфорации распечатывается вся исходная информация рассчитываемого варианта. При этом печатаются необходимые комментарии (см. пример.).
Для каждого элемента для трех его сечеиий — в начале, середиие и конце в первой таблице (см, пример) печатаются значения изгибающего! момента, продольного осевого усилия, поперечной силы, поперечного и про- t дольного перемещения. Знак плюс прн изгибающем моменте означает, что • при изгибе трубопровода растянуты правые волокна, если смотреть от начала 1 к концу элемента. Знак плюс при продольном осевом усилии в стенках трубы означает, что осевое усилие растягивающее. Знак плюс при поперечной силе! указывает на то, что на левом конце элемента поперечная сила сдвигает этот конец вверх, а на правом конце — вниз. Знак плюс при значении попе-1 речного перемещения означает, что даппое перемещение направлено вниз,! перпендикулярно данному элементу. Знак плюс при значении продольного 1 перемещения означает, что перемещение направлено вдоль элемента, от его начала к его концу.
Далее, на печать выдаются узловые усилия в начальной и конечной ' точках рассчитываемого участка трубопровода Л (см. рис. 41, а). Положи-1 тельные направления этих усилий в случае примыкания рассчитываемой коИ-1 струкции А к магистрали В сверху показаны на рис. 41, а. Усилия печатз- 1 ю ся по порядку от первого до шестого, причем первые три соответствуют „згнбающему моменту, поперечной силе, продольному усилию для начальной тс,чни рассчитываемой конструкции Л, а вторые три —для конечной точки эт0й конструкции. На примыкающую конструкцию В действуют усилия про-Т1 аоположиого направления. Положительные направления усилий в случае примыкания рассчитываемой конструкцции А к магистрали В снизу показаны на рис. 41,6. Если части Л и В соединены под прямым углом (тройником), то для последующего расчета части В, примыкающей снизу (см. рис- 41,6), величины внешних усилий будет равны: в начальной точке:
Z первому числу (из шести напечатанных) со своим знаком; Z2—третьему числу со своим знаком; Z3 — второму числу с противоположным знаком; в конечной точке:
2, — четвертому числу с противоположным знаком; Хч—шестому числу со своим знаком; Z3 — пятому числу с противоположным знаком.
При расчете части В, примыкающей сверху (см. рис. 41,6), во входной информации внешние усилия будут равны: в начальной точке:
Z - первом}’ числу со своим знаком; Тг— третьем}’ числу с противополож-ним знаком; Z3 —второму числу со споим знаком; в конечной точке:
7,—четвертому числу с противоположным знаком; ?2 — шестому числу с противоположным знаком; Z3 — пятому числу со своим знаком.
При произвольном наклонном положении магистрали В выбор значений величин внешних усилий во входной информации осуществляется поворотом рис. 41, а или б до положения рассчитываемой схемы
Во второй таблице для ранее указанных сечений приведены следующие величины:
в первом столбце — значения изгибающего момента с учетом геометрической нелинейности (продольно-поперечного изгиба);
во втором столбце — значения фибровых напряжений в растянутой (с точки зрения изгиба) зоне сечения (знак плюс — растяжение);
в третьем столбце — предельно-допускаемые напряжения, вычисленные по СНиП 11-45—75 для этого сечения;
в четвертом столбце—значения фибровых напряжений в сжатой зоне сечения;
в пятом столбце — предельно-допускаемые напряжения, вычисленные по СНиП II-45—75 для этого сечения.
Выводы, печатаемые в выходной информации, основаны на сравнении действующих напряжений с пределыю-допускаемыми.
Если не выполняется условие (7.32), то печатается вывод, что толщина стенкн трубы или детали (отвода) не достаточна. Если такого вывода нет, то проверяется второе условие (7.33) и печатается соответствующий вывод.
Приведем пример использовании программы «Шаг лента» при расчете подземного компенсатора-упора. Компеисаторы-упоры применяются для уменьшения перемещений подземного трубопровода в месте выхода его на поверхность, уменьшения усилий, передаваемых на конструкции, к которым подходит подземный трубопровод. Конфигурация компенсатора подбирается из . словия минимальных перемещений на его конце при ограничениях напряжений п трубопроводе. В связи с этим при применении компенсатора-упора трапецеидального очертания угол, примыкающий к длинному прямолинейному участку, обычно в 1,5—3 раза меньше угла, примыкающего к концевому участку. На рис. 42 изображен один из таких компенсаторов с углами 36° н 75°, вылетом 43 м и длиной 180 м, применяемых при проектировании газопроводов больших диаметров. Углы поворота 36° осуществлены из набора отводов с углами 6°, выполненных гиутьем, с прямолинейными участками между ними.
равными 3,2 и 7,8 м. Угол поворота 75° выполнен из крутозагиутого отвод радиусом 710 см (5 ?>„) Компенсатор упор выполнен нз труб 1420X19,5 мм ftIй=600 МПа, Я2Н=470 МПа. Компенсатор-упор расположен на учас7^
II категории, следовательно, согласно СНиП I1-4S—75 коэффициент условия работы »»=0,75, коэффициент, отражающий категорию, с=0,85, рабочее (нор' мативное) давление продукта р=7,5 МПа, положительный температурив перепад &t=57 °С. Физико-механические характеристики грунта постоянна по длине рассчитываемого участка: грунт песчаный, Vrp=15 кН/м3, <рГр=24° Сгр=0,001 МПа, ?гр=20 МПа, рГр=0,25, с* о=0,02 МПа/см, RTР=0,2 МПа!
Граничные условия по Концам рассчитываемого участка: левый конец свободеп, поэтому податливости приняты равными бесконечности и записаны в виде 0,1 1021, правый конец, примыкающий к длинному прямолинейному участку, «а расстоянии примерно 500 м считаем защемленным, поэтому щ три параметра податливости на койне принимаем равными нулю.
Схема разбивки рассчитываемого участка на конечные элементы при дена иа рис. 42. Отметим, что счет элементов начинаете к с двух. Криву угла поворота в 75° разбиваем на пять прямолинейных элементов, тогд
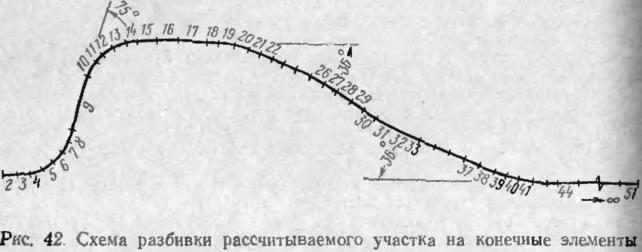
угол между элементами будет 75/5=15°, а между крайним и прямолинейным-
a
75/5-2=7,5°, Длина каждого элемента /п=2рsin——= 2-710sin 7,5°=185см.
2п
Длины элементов, образующих угол 36°, приняты согласно данным о гнутым отводах (длины элементов (в см) см. в выходной информации) Отметим j также, что глубина заложення газопровода изменяется от 100 до 150 см,| а расстояние от трубы до стенкн траншеи принято 30 см, за исключепием участков с крутозагнутыми отводами, где оно составляет 60 см. Распечатка информации, выдаваемой на печать, следующая. Первая часть содержит не-! ходные данные для расчета, которые служат для контроля правильности под-' готовки даииых. Вторая часть содержит результаты расчета, третья часть — ¦ прочностной расчет.
Остановимся кратко иа анализе результатов. Вначале проверяем пра- < вильность принятой предпосылки, можно ли синтать, что газопровод защем-' лен на расстоянии 500 м. Контролем могут служить данные об усилиях иа нравом конце рассчитываемого участка. Из таблицы результатов расчета находим, что для 51 участка при координате, равной единицы
—0,103-10~12 Н-м, JV=—0,557-107 Н, Q=-0,506.10 ieH. Отсюда видноЗ что изгибающий момент и поперечную силу можно считать равными нулю.] Определим усилие для данного сечепия трубопровода при отсутствии перемещений
pDHH 7,5-138,1 Кольцевые напряжения <тКц = ——--- -— — = 265,6МПа. Усилие''
X859,5==—0,55.10* МПА-см —0,55 • 107 Н, что практически совпадает с полученным результатом.
Далее, обратим внимание на вывод, что конструкция удовлетворяет ус-ювням по деформациям. Это означает, что с точки зрения напряженно-деформированного состояния трубопровода конструкция удовлетворяет требованиям норм по предельным состояниям.
Посмотрим, каковы усилия и перемещения в начале компенсатора-упора, т е. для второго участка при координате, равной нулю. Изгибающий момент и поперечная сила практически равны нулю, продольное усилие, равное 0,112-10* Н, представляет собой усилие от давления на заглушку P^=pFсв =
nDlu „ П138-1*
= р —-—= 7,5- -= 0,112- 10вМПа-см = 0,112- 10ВН. Поперечное пере-
4 о
гашение составляет 0,56 см, продольное—1,4 см, полное перемещение —
| 0,56г+1,442=1,55 см. При отсутствии компенсатора-упора продольное перемещение было бы более чем в 10 раз выше, т. е. даипая конструкция существенно уменьшила перемещение трубопровода.
Представляет интерес характер и величина перемещений по длине рассчитываемого участка. Например, на первом углу поворота для середины седьмого участка поперечное перемещение равно 2,4 см, а продольное —
1,05 см, для середины двенадцатого соответственно —11,1 и —5,2 см. Для остальных углов поворота, выполненных плавной кривой, перемещения незначительны.
Рассмотрим напряженное состояние трубопровода. Наибольший изгибающий момент, равный —0,190-10 Н-м, возникает в начале 14 элемента, т. е. во втором угле поворота. Напряжения в растянутой зоне сечения при этом равны 240 МПа, что меньше предельио-допускаемых, равных 363 МПа, в 1,5 раза.
Напряжения на участках, выполненных отводами машинного гнутья, незначительны. Это показывает, что для данного конкретного случая угол поворота трапецеидального компенсатора, принятый равным 36°, можно уве-* лкчить, или уменьшить параметры (вылет) компенсатора-упора. Методом вариантного проектирования можно выбрать для конкретных условий рациональное очертание компенсатора-упора, например, из условия минимума его длины.
Выходная информаций
Заказ: Вэряант:
Расчет подземного участка трубопровода с произвольным очертанием оси в горизон аяьнай плоскости
(Шаг — лента)
Исходные данные:
Отдел:
Объект
Дата:
Удельный вес металла, кН/м3
Коэффициент Пуассока металла
Коэффициент надежности
Наружный диаметр магистрали справа, см
Толщина стеики магистрали справа, см
Высота засыпки труб справа, см
Расстояние от трубы до стенки траншеи справа, см
78,5
0.3
1.10
о
0.0
0.
0.
| Ф. град | 1 Р* | см |
| 00 | ЛООЕ |
21 |
| —7 50 |
ЛООЕ | 21 |
|
—15.00 | .710Е | 03 |
| —15 00 | .710 Е | 03 |
| -15.00 |
• 710Е | 03 |
|
—15.00 | .71ОЕ | 03 |
| —7.50 | .71ОЕ | 03 |
| 7.50 |
ЛООЕ | 21 |
|
15.00 | .71 ОЕ | 03 |
| 15 00 | 710Е |
03 |
| 15.0 |
.71DE | 03 |
|
15.00 | -710Е | 03 |
| 15.00 | .710Е |
03 |
| 0.0 |
ЛООЕ | 21 |
| 0 0 | ЛООЕ | 21 |
| 0.0 | 100Е |
21 |
| 3.00 |
100Е | 21 |
|
3.00 | •710Е | 03 |
| 3.00 | ЛООЕ |
21 |
Номер
участка
МПа
At, °С
V
6, см
см
см
h, см
2
3
4
5
6
7
8 9
10
11
12
13
14
15 36
17
18
19
20
7.5
7.5
7.5 75 7 5
7.5
7.5
7.5
7.5
7.5
7.5
7.5
7.5
7.5
7.5
7.5
7.5
7.5
7.5
57.0
57.0
57.0
57.0
57.0
57.0 57 0
57.0
57.0
57.0
57.0
57.0
57.0
57.0
57.0
57.0
57.0
57.0 57 0
142.
142.
142.
142.
142.
142.
142.
142
142
142.
142.
142.
142.
142.
142.
142.
142.
142
142
1.95
1.95
1.95 1 95
1.95
1.95
1.95
1.95
1.95 1.9 5
1.95 1 95
1.95
1.95
1.95
1.95
1.95
1.95
1.95
1420
710
185
185.
185.
185.
185.
3052.
185.
185.
185.
185.
185.
800
800
1257.
530.
628.
320
0.85
0.85
0.85
0.85
0.85
0.85
0.85
0 85
0.85
0.85
0.85
0.85
0.85
0.85
0.85
0.85
0.85
0.85
0.85
100. 100. 100. 100. 100. 120. 120. 120. 120. 120. 100. 100. 140. 140. 10 0 100. 110. 110. И0.
¦
Продолжение
h, см
в, см
I, см
Ч>. град
м, °с
МПа
о, см
Номер
участка
110.
ПО.
100.
150.
150.
150.
150.
150.
150.
150.
150.
150.
100.
100.
100.
100.
100.
100
100.
100.
100.
100.
100
100.
100.
100.
100.
100
100.
100.
100.
0 85
0.85
0.85
0.85
О 85
О 85
0.85
0.85
0.85
О 85
0.85
0.85
0.85
0.85
0.85
0.85
О 85
О 85
О 85
0.85
О 85
О 85
0 85
O.S5
О 85
0.85
0.85
О 85
0.85
0.85
О 85
.710Е 03 • 100Е 21 ¦710Е 03 .100Е 21 .7L0E 03 ЛООЕ 21 •710Е 03 .1CI0E 21 .7J0E 03 ЛООЕ 21 .710Е 03 ЛООЕ 21 .710Е 03 ЛООЕ 21 .710Е 03 ЛООЕ 21 •710Е 03 100Е 21 .710 Е 03 ЛООЕ 21 .710Е 03 Л00Е 21 ЛООЕ 21 Л00Е 21 ЛООЕ 21 ЛООЕ 21 ЛООЕ 21 100 Е 21 Л00Е 21 -100Е 21 ЛООЕ 21
3.00 300
3.00 3 00
3.00
3.00
3.00
3.00 —3.00 —3.00 —3,00 —3.00 —3.00 —3.00 —3 00 —3.00 —3.00 —3.00 -3.00 —3.00 -3.00
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
628.
780.
628.
320.
628.
780.
628.
320.
628.
780.
628
320
628.
780.
628
320.
628.
780.
628.
320
628.
530.
710.
1420.
2130.
4260.
6390.
7500
7500
7500.
7500.
1 95
1.95
1.95
1.95
1.95
1.95
1.95
1.95
1.95
1.95
1.95
1.95
1.95
1.95
1.95
1.95
1.95
1.95
1.95
1.95
1.95
1.95
1.95
1.95
1.95
1.95
1.95
1.95
1.95
1.95
1.95
142
142.
142.
142.
142
142.
142.
142.
142.
142.
142,
142.
142.
142.
142.
142.
142.
142.
142.
142.
142.
142.
142.
142.
142.
142.
142.
142.
142.
142.
142.
57.0
57.0
57.0
57.0
57.0
57.0
57.0
57.0 57 0
57.0
57.0
57.0
57.0
57.0
57.0
57.0
57.0
57.0
57.0
57.0
57.0
57.0
57.0
57.0
57.0
57.0 57 0
57.0
57.0
57.0
57.0
7.5
7.5
7.5 7 5
7.5
7.5
7.5
7.5
7.5
7.5
7.5
7.5
7.5
7.5
7.5
7.5
7.5
7.5
7.5
7.5
7.5
7.5
7.5
7.5
7.5
7.5
7.5
7.5
7.5
7.5
7.5
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
| Номер участка | а, см |
я". МПа | PRG |
Vrp' taHjM8 | <S>rp. град | сгр, МПа |
! мНа | ^гр |
гхо' МПа см | Rrp. МПа |
| 2 |
30. | 470 | 0 |
15 | 24. | .001 |
20 | .25 | 020 |
0.2 |
| 3 |
60. | 470 | 0 |
15 | 24. | .001 |
20 | .25 | .020 | 0.2 |
| 4 |
60. | 470 | 0 |
15 | 24. | .001 |
20 | .25 | .020 | 0.2 |
| 5 |
60. | 470 | 0 |
15 | 24. | .001 |
20 | 25 | ,020 |
0.2 |
| 6 |
60. | 470 | 0 |
15 | 24. | .001 |
20 | .25 | -020 | 02 |
| 7 |
60. | 470 | 0 |
15 | 24. | .001 |
20 | .25 | .020 | 0.2 |
| 8 |
60. | 470 | 0 |
15 | 24. | 001 | 20 | .25 |
.020 | 0.2 |
| 9 | 30. | 470 | 0 | 15 | 24. |
001 | 20 | .25 |
.020 | 0 2 |
|
Ю | 60 | 470 |
0 | 15 | 24. |
.001 | 20 | .25 |
.020 | 0.2 |
|
11 | 60. | 470 |
0 | 15 | 24. |
.001 | 20 | .25 |
.020 | 02 |
|
12 | 60. | 470 |
0 | 15 | 24. |
.001 | 20 | .25 |
.020 | 0.2 |
|
13 | 60 | 470 |
0 | 15 | 24. |
.001 | 20 | .25 |
.020 | 0.2 |
|
14 | 60. | 470 |
0 | 15 | 24. |
.001 | 20 | .25 |
.020 | 0,2 |
|
15 | 30 | 470 |
0 | 15 | 24. |
.001 | 20 | .25 |
020 | 0.2 |
|
16 | 30. | 470 |
0 | 15 | 24. |
.001 | 20 | .25 |
.020 | 0.2 |
|
17 | 30 | 470 |
0 | 15 | 24. |
.001 | 20 | .25 |
.020 | 0.2 |
|
18 | 30. | 470 |
0 | 15 | 24. |
,001 | 20 | ,25 |
.020 | 0.2 |
|
19 | 30. | 470 |
0 | 15 | 24. |
.001 | 20 | .25 |
.020 | 0.2 |
|
20 | 30. | 470 |
0 | 15 | 24. |
.001 | 20 | .25 |
.020 | 0.2 |
|
21 | 30. | 470 |
0 | 15 | 24. |
.001 | 20 | .25 |
.020 | 0.2 |
|
22 | 30. | 470 |
0 | 15 | 24 |
.001 | 20 | .25 |
.020 | 0.2 |
|
23 | 30. | 470 |
0 | 15 | 24. |
.001 | 20 | .25 |
020 | 0.2 |
|
24 | 30, | 470 |
0 | 15 | 24. |
.001 | 20 | .25 |
.020 | 0.2 |
|
25 | 30. | 470 |
0 | 15 | 24. |
.001 | 20 | .25 |
020 | 0.2 |
|
26 | 30. | 470 |
0 | 15 | 24. |
.001 | 20 | .25 |
.020 | 0.2 |
|
27 | 30. | 470 |
0 | 15 | 24. |
.001 | 20 | .25 |
.020 | 0.2 |
|
28 | 30. | 470 |
0 | 15 | 24. |
001 | 20 | .25 |
.020 | 0.2 |
|
29 | 30 | 470 |
0 | 15 | 24. |
.001 | 20 | .25 |
.020 | 0.2 |
|
30 | 30. | 470 |
0 | 15 | 24. |
.001 | 20 | .25 |
.020 | 0.2 |
|
31 | 30. | 470 |
0 | 15 | 24 |
001 | 20 | .25 | 020 | 02 |
град
кН м3
Фгр'
угр’
24.
24.
24.
24
24.
24.
24.
24.
24.
24.
24.
24.
24.
24.
24.
24.
24.
24.
24.
24.
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
| Ноиер участка | 0, см | «2 ' МПа | РЯС |
|
32 | 30- | 470 |
0 |
| 33 |
30. | 470 | 0 |
| 34 | 30. | 470 | 0 |
| 35 |
30. | 470 | 0 |
| 36 | 30. | 470 | 0 |
| 37 |
30. | 470 | 0 |
| 38 | 30. |
470 | 0 |
| 39 | 30. | 470 | 0 |
| 40 | 30. |
470 | 0 |
|
41 | 30. | 470 |
0 |
| 42 | 30. | 470 | 0 |
|
43 | 30. | 470 |
0 |
| 44 |
30. | 470 | 0 |
| 45 | 30. | 470 | 0 |
| 46 |
30. | 470 | 0 |
| 47 | 30. | 470 | 0 |
| 48 |
30. | 470 | 0 |
| 49 | 30. |
470 | 0 |
| 50 | 30 | 470 |
0 |
| 51 |
30. | 470 | 0 |
П р О Л О Л Ж с U и с
-р’
| , МПа | | М^а | **гр | |
СХО' МПа см | V ип |
| .001 |
20 | .25 | .020 |
0.2 |
| .001 |
20 | .25 | .020 |
0.2 |
| .001 |
20 | .25 | .020 |
0.2 |
| .001 |
20 | .25 | .020 |
0.2 |
| .001 |
20 | .25 | .020 |
0.2 |
| 001 |
20 | .25 | .020 |
0.2 |
| .001 |
20 | .25 | .020 |
0 2 |
| 001 |
20 | .25 | 020 |
0.2 |
| 001 | 20 | .25 | .020 |
0.2 |
| 001 | 20 | .25 | .020 | 0 2 |
| 001 | 20 | .25 | .020 |
0.2 |
| 001 | 20 | .25 | .020 |
0.2 |
| 001 | 20 | .25 | .020 |
0.2 |
| .001 | 20 | .25 | .020 |
0.2 |
| .001 | 20 | .25 | 020 |
0.2 |
| .001 | 20 | .25 | .020 |
0.2 |
| .001 | 20 | .25 | .020 |
0.2 |
| .001 | 20 | .25 | .020 |
0.2 |
| .001 | 20 | .25 | .020 |
0.2 |
| 001 | 20 | .25 | j .020 |
0.2 |
сЗН 0.10000 Е 21
с1К
0.0
с2К
00
СЗК
0.0
с1Н с2Н
0 10000 Е 21 0.10000 Е 21
Результаты расчета
Ноиер
участка
Координаты
| 2 | 0.0 |
| 2 | 0.5 |
| 2 | 1.0 |
|
3 | 0.0 |
| 3 | 0.5 |
| 3 |
1.0 |
| 4 |
0.0 |
| 4 | 0.5 |
| 4 | 1 0 |
| 5 | 0.0 |
|
5 | 0.5 |
| 5 | 1.0 |
| 6 |
0.0 |
| 6 | 0.5 |
| 6 | 1.0 |
| 7 | 0.0 |
|
7 | 0.5 |
| 7 | 1.0 |
| 8 |
00 |
| 8 | 0 5 |
| 8 | 1.0 |
| 9 | 0 0 |
| 9 | 05 |
|
9 | 1 0 |
| 10 | 0.0 |
Изгибающий
Продольное усилие, Н
момент»
Н*м
—.1995Е —.1928Е —.4236Е —.4236Е —.3602Е —.5680Е — 5680Е 0.2746Е 0.1393Е 0.1393Е 0.1910Е 0.2752Е 0.2751Е 0.2949Е 0.3492Е 0.3492Е 0.3218Е 0.3296Е 0.3296Е 0.2362Е 0.I724E 0.1724Е 0.1296Е 0 8542Е О 8541Е
|
00 | 0.1123Е | 08 |
| 06 | 0.1087Е |
08 |
| 06 | 0 Л 071Е | 08 |
| 06 | 0.1071Е | 08 |
| 06 | 0.1072Е | 08 |
| 05 | 0.1083Е |
08 |
| 05 |
0.1081Е | 08 |
|
05 | 0.1084Е | 08 |
| 06 | 0.1087Е |
08 |
| 06 | 0 1085Е | 08 |
| 06 | 0.1084Е | 08 |
| Об | 0.1083Е | 08 |
| 06 | 0.1082Е |
08 |
| 06 |
0.1078Е | 08 |
|
06 | 0.1075Е | 08 |
| 06 | 0.1075Е |
08 |
| 06 |
0.1071Е | 08 |
|
06 | 0 J067E | 08 |
| 06 | 0 1069Е |
08 |
| 06 | 0 1065Е | 08 |
| 06 | 0 1061Е | 08 |
| 06 | 0.1062Е | 08 |
| 07 | 0.9288Е |
07 |
| 06 |
0.9680Е | 07 |
|
Об | 0.960! Е | 07 |
Поперечная сила, Н
| 0.3974Е- | -01 |
| —.4299Е | 05 |
| —.5568Е | 04 |
| —.5568Е | 04 |
| 0.4621 Е | 05 |
| 0.1306Е | 06 |
|
0.7700Е | 05 |
|
0.1056Е | 06 |
|
0.1367Е | 06 |
|
0.3907Е | 05 |
|
0.7307Е | 05 |
|
0.1091Е | 06 |
|
0.321 ЭЕ | 04 |
|
0.3980Е | 05 |
|
0.7765Е | 05 |
| — .4841Е | 05 |
| —. 1061Е | 05 |
|
0.2738Е | 05 |
|
—.1172Е | 06 |
|
—.8480Е | 05 |
|
—.5326Е | 05 |
|
— .1334Е | 06 |
|
0.2073Е | 06 |
|
—.6946Е | 06 |
|
—.4858Е | 06 |
Поперечное
перемещение,
см
| —.5574Е |
00 |
| — .5747Е- |
-01 |
| 0.6671Е |
00 |
| 0 6671Е |
00 |
| 0.Ш4Е |
Oi |
| 0.1819Е |
01 |
| 0.1868Е |
01 |
| 0.2039Е |
01 |
| 0 2207Е |
01 |
| 0 2242Е |
01 |
| 0 2396Е |
01 |
| 0.2527Е |
01 |
| 0.2444Е |
01 |
| 0 2546Е |
01 |
| 0.2614Е |
01 |
| 0.2401Е |
01 |
| 0.2432Е |
01 |
| 0.2426Е |
01 |
| 0.2092Е |
01 |
| 0.2051 Е |
01 |
| 0.1983Е |
01 |
| 0.1784Е |
01 |
| 0.2448Е |
00 |
| — 8155Е |
01 |
| — 8205Е |
01 |
Продольное
перемещение,
си
— .1443Е 01
— .7886Е 00
— .1438Е 00
— 1439Е 00 0 1771Е 00 0.4993Е 00 0.2577Е 00 0.3419Е 00 0 4264Е 00
— .1595Е 00 —.75J7E-01
0 9142Е—02 —.6454Е 08 —.5613Е 00 —.4773Е 00 —.1137Е 01 —.1053Е 01 —.9702 Е 00 —.1565Е 01 —.1481Е 01 —.1398Е 01 —.1645Е 01 —.3417Е 00 0.9223Е 00
— 1499Е 00
Продолжение
|
Ноиер участка |
Координаты |
Изгибающий момент, Н м | Продольное усилие, Н | Поперечная сила, Н | Поперсчпое перемещение, см | Продольное перем ещение* см | ||||
| 10 | 0.5 | 0.3433Е | 06 |
0.9593Е | 07 | — .6209Е | 06 | — 9100Е |
01 | — .7202Е—01 |
|
10 | 1 0 | — 2989Е |
06 | 0 9591Е | 07 | —.7703Е | 06 |
— 1003Е | 02 | 0 5890Е—02 |
| 11 | 0 0 | — 2988Е | 06 |
0.9447Е | 07 | — .3188Е | 06 | — .9692Е | 01 | — 2591Е 01 |
| 11 | 0.5 | — .6660Е | 06 | 0.9409Е |
07 | —.4773Е | 06 | —. 1059Е | 02 |
— 2513Е 01 |
| 11 |
1.0 | —.1186Е | 07 |
0.9372Е | 07 |
—.6495Е | 06 | — .И42Е | 02 | — .2437Е 01 |
| 12 | 0.0 |
—.1186Е | 07 | 0.9267Е | 07 | — 1455Е |
06 | — .1040Е | 02 |
— 5310Е 01 |
| 12 |
0.5 | — 1392Е | 07 | 0.9233Е | 07 |
—.3032Е | 06 | — 1110Е | 02 | — 5234Е 01 |
| 12 | 1.0 | — I 50Е | 07 | 0.9200Е |
07 | —.4702Е | 06 | — 1165Е | 02 |
— 5158Е 01 |
| 13 |
0 0 | — 1750Е | 07 |
0.9147Е | 07 |
0.7228Е | 05 | — .9919Е | 01 | — 7997Е 01 |
| 13 | 0.5 | —. 1751Е | 07 | 0.9113Е |
07 | —.7586Е | 05 | — .10276 | 02 |
— .7921Е 01 |
| 13 |
1.0 | —.189IE | 07 |
Q.9080E | 07 |
—.2277Е | 06 | —.1042Е | 02 | —.7845Е 01 |
| 14 | 0.0 |
— 1891Е | 07 |
0.9094Е | 07 | 0.3375Е | 06 | —.S040E |
01 | —.1027Е 02 |
| 4 | 0.5 | — 1641Е | 07 | 0.9053Е |
07 | 0.2055Е | 06 |
— .7989Е | 01 |
—.1020Е 02 |
| 14 |
1 0 | — 1510Е | 07 |
0 9012Е | 07 |
0.7595А | 05 | —.7750Е | 01 | —.1012Е 02 |
| 15 | 0.0 | — 1510Е | 07 | 0.9108Е |
07 | 0.6483Е | 06 | — .4865Е | 01 |
— .1178Е 02 |
| 15 |
0.5 | 0.3521 Е | 06 |
0.8928Е | 07 |
0.3048Е | 06 | — .3317Е | 01 | —.1146Е 02 |
| 15 | 1.0 | 0 1101Е | 07 | 0.8754Е |
07 | 0.9003Е | 05 | — 1863Е | 01 |
—.1114Е 02 |
| 16 |
0.0 | 0 1101Е | 07 |
0 8754Е | 07 |
0.9004Е | 05 | — 1863Е | 01 | —.1114Е 02 |
| 16 | 0.5 |
0.1234Е | 07 | 0 8605Е | 07 | —.9618Е |
04 | —.7902Е | 00 |
—.1082Е 02 |
| 16 |
1.0 | 0.1112Е | 07 | 0 8461Е | 07 |
—.4339Е | 05 | — .1562Е | 00 | —.1051Е 02 |
| 17 | 0.0 |
0.1112Е | 07 | 0.8461Е | 07 | — .4339Е |
05 | — .1562Е | 00 |
—.1051Е 02 |
| 17 |
0.5 | 0 8342Е | 06 | 0.8226Е | 07 |
— 4082Е | 05 | 0.5403Е | 01 | — .1002Е 02 |
| 17 | 1.0 |
0.5502Е | 06 | 0.8002Е | 07 | —.6050Е |
05 | — .4831Е | 00 |
— 9550Е 01 |
| 18 |
0.0 | 0.5502Е | 06 | 0.8002Е | 07 |
—.6050Е | 05 | — .4831Е | 00 | — 9550 Е 01 |
| 18 | 0.5 |
0.3477Е | 06 | 0.7898Е | 07 | —.9570Е |
05 | — .8722Е | 00 |
— 9351Е 01 |
| 18 |
1.0 | 0.2351Е | 05 | 0.7797Е | 07 |
— .1528Е | 06 | —.1314Е | 01 | — .9153Е 01 |
| 19 | 0.0 | 0.2351 Е | 05 | 0.7794Е |
07 | 0.2719Е | 05 | —.8340Е | 00 |
—.9209Е 01 |
| 19 |
0 5 | 0.9734Е | 04 |
0.7671Е | 07 |
—,4179В | 05 | — .1396Е | 01 | —.8977Е 01 |
| 19 | 1 0 |
—.2762Е | 06 | 0.7551 Е | 07 | —.1460Е |
06 | —.1941Е | 01 |
—.8747Е 01 |
| 20 |
00 | — .2763Е | 06 | 0.7548Е | 07 |
0.4683Е | 05 | — 1480Е | 01 | —.8838Е 01 |
Продолжение
Плодил ж ^ » 11 е
S<5 К S3 к
§=Г* о fl>
p. CL
инц
<M-5S* ^
О о »«*•
coSS
Ш ри ш
СО LTD to
<о ^ со " см со 00 оо
ш ш ш
сч <?> -3* счосЬ г- 25 со оо со оо
ш
Ы К
2*
S3 о
SHg
о« g a)S° p <u a o.
Ct>
с
иЛ Щ щ
o-^of
О") со i NT «Ь lO
N^io 4
oo
Ю СОЮ ООО
Ю iO <D ООО
сОСОсО!
о ooi
ШЙШ
т c^-
TMDN CD CS CO —« CM
ШШШ
сч ^ <o ] СО о •—« — Сч! —<
Sx
ООО
I I
oo oo
SgK
Si
p.**
с
CDiDNTJ-^CDCN^CNifl^a)^.
oocNCMOoooococvcocPio^t^t
lD CD сО ООО
ЮЮ
о о шеи
Ю to СО CD
юю см Сч
CO CD CD
ooo
CD со о о
to со со CD со оо оо о
CO CO CD ooo
< Ю Ю CD ) о oo
? b
ШШШ
Г- cO —.
о ^ ^
CM CM CM
шшш
со сч см со оо 00 стою —«см см
ЩИШ «
CO cr> O CO CM CM CO LO Ю .
INTj-'f
* oo
ШШШ
00 00 00 t'-* о о о CO
40 ю CM
WWffl
О Ю) ю 5>смсм
СО LO LO
|Л см сч
шш
СОСО
смеч
Г4* 05
ЩЩШИШ
t- СО t’-о О CD оо 00 СМ СЧ 05 CD CD h- CD t— r-
•gl51
f~ s
sS
Л Г1
О П *?
ЗооЗооооооооооооооооооЗЗ
ujajijjuJijjajwijjajwujtjjaJWwajwuJaJtdLLi —«ОСМЮ—00О> — СЧСОСОЮСМСЧООО^СОО—
tOCCot-'CDl'-^DCOt'-cDiOcD — *ЬЭ000}0>О»-**-»«с0
St— 00 с?> ^ Ю ^ т*м5Ч о С7> СО 1^- LO СО ^ СО СО l'-*r'4t'-l'-'r''-t'-t'-t'-t"-t'-r*-cDcDcOcDCDcOcOcD<D
I I I I I I Г Г Г Г Г Г ГI (' I ГI' I ГI' I I' ГI I I'
OOOOOOOOOOOOOOOOOOOOOOOOOOO
МЙШШШ W Ш W Ш ШШ щ Ш Ш UJ Ш Ш Id Ш щ Ш Ш Ш Ш Щ td Ш
O CM 00 ^ CO CO CD Ю CD N't °з п со ro <o CM О t"— CD оо Ю *—« со
ООЮМ^!М .-*с?>ЮГ—COCOt'-O)—‘СОЬ-ОООССО-^Ю—«CO--*!^ Г'-С7>тГГ--О5ЮС0—>Г"-0-** O^CNOiOWOiCNiOCNTj'nOblfl^ —< — — .—icn—«счсчс-дсчсч—«счеч—'счсчсчсчо^сч — —
ю о о о о *o О О 'Л о О 'Л О О 'Л о о о о ю о О iO о о ю о о 0^00—00—00— ОО—'ОО—'OO—OO—ОО^ОО— о
ЙШИИЩШИИИШЩШИШШИШШИШ1
^C0N(?>00Q(?>CQi^Ln<N^P:N00t#;-*J'O<Nr't <?> ao c* О ¦*>* M lOOlOrtOONCD^OCN'-'^’ РСООЛЛСО^-^РЗСЧОООЬЬЬО^СО-ЧОС CD CO Is" — 00 —•OOCO^t'-'*4t"-~-'CO~^^—* СЧ t"- <
О О — — — СЧСМСЧСОСОСО-^^^ЮЮЮСОСОСОГ^Г^Ь-ООООСОСЛОО^О СЧСЧСМСЧСЧСЧСМСЧСЧСМСМСМСМСЧСМСЧСЧО^СЧСЧСЧСЧС^СЧСЧСМСМСМСМСО'
I I I I I I I I I I I I I I I I I I I I I II I I I I I
|
г- | г- |
г- | г- | г- |
г— | |||
| О |
О | о | о |
о | о | о |
о | о |
|
Ш | Ы | ttj | щ | щ |
ш | LU |
ш | ш |
|
ю | сч | СО |
СЛ | оо |
о | со | ||
| ю СО | см |
•'"Н <м |
см 8 | т 00 |
е | LO LO |
ю LO | |
| СО |
to | со | ю |
ю | ю |
ю | ю | |
|
О | О | о |
о | о | о |
о | о | о |
oooooooooooooooooooo
I ° I I ° I 1°'
ШЩИШШ щ оо оо счсо
СО СОСО ю см
-ЧСЧ«МЮЬ СО СО СМ
Ю ю LO CD CD
ооооо
О О О О О ОС
SSF1
| . « % S" 2§ 43S &S ° О <и Сьр. Г- Ш 1 и с |
5SoSSooSoООООООООООООООООООООО WBjBJMuaiuwgWBJwgujwwgwMMgwgwgMMgg^g, да? |
| sl= <у S 5Р О» О о. у— й) ^ с |
liiiiileiill ОООООООООООООООООООО |
| га 4 5 о к 5х <и р. о С о С | gggsssssssssssssssssssssssssss “иишйёё |
|
Продольное усилие, |
lliiillllllllSSlsisIs |
| « я * * * к о *- к го S |
8Sg8SSggSSS8SSSS*s*"§8SSSSSSSS ИИШИШИШИИШМШИМШИЩШШИИИМИ^^д^^ |
| ординаты |
dS2o2dS26dS§S2dS2dd°do2gd2od°§ |
| 1 О * | |
| Номер участка | aasssaaaasasss^sssfcftfesassss? |
Продолжение
о о оо
о о о о
О *
4 - 5:
о о g 0
О й> 0.0.
H <i>
*~ч с
OOOOOOOOOOOOOOOOOOOOO
ттт
ШШЦ
LO Ю CQ Ю Ю 00 03 03 00
оо со со
Тп
ШЩ]
Й1^ 4
00 00 о
СО СО
шии
NtO't ^ ^ ^
шш
oS
шш
ЮЗО СО 03
n о
см см
ЩЙ
Оз СМ N lO
00 N
СО Tt'
иш
СО ю
323
шыш 0^0 СО — О
-rj*
иш
со СО
СМ
10 10
ШИ
см со ю о Lr 0
см
СЧМЛЮЮСОЮ О О СО СО CO СО
—« —« GO LO LO —, г--
^ ^ СО СО СО СО СМ
I I I I I I I I I I I I I I I I I I I I I I I I I I I и
со со 00
ООО
I I I
ищи
ОО ОО Оз СО со'О ООО
CMcO
“ о
CM CM
о о
I I
1ИИ ' coco
CO CO
00
do
OOOOOOOOOSOOOOOO
I
ШИИШИИИЙШИИИИИШИ
-|(NCJ)-.0(N'-O>0^c0i0icc000-' N03Tr,^.— t''03-tf<-^<cONN —«СЯСЧ1Л
cscs ON -нСО-н lfclQrr'^^f-^CO<OiO ^тГ^СОСОСЛСЛ—<OOCOcO—^—«— OOOOOOOOOOOO
TT-TT
о ?
*1 о> 3 S с.«5 us
С О о о.
ШШ
CO 00
S3
—* CM
О I*
ШИ со 04 -3* ^
со о
СМ —
1° I I
1C со CD LO со О о о оо
COOiOiO^fLOiOiOlOiO^f^f^fCSCS
ООООООООООООООО
ИИИИЫИИЫШЫШШЩЫИ
| Оз | 03 | ОО | *Q |
со | см | 03 |
03 | со |
|
СО | 00 | СМ |
об | ОО | N | со | со |
N |
| СО | СО | со | см | |||||
|
со | со |
см | СМ | СМ |
см | СМ | тГ< | |
| о | о |
d | о | о |
о | г | г |
г |
СО ^ «З4 СО
тттт
шшшщ
СО со iD СО СО 03 О} ю Г- CM СМ —. — —I —« ю
N
о
I
щщ
03 03
оо
СМ -Ч —• —
о о
тт
шш
СМ СМ
о о о о
т
шшизыш
СО со Оз —i 03 Tt* 03 СО N «СОСО-^in
СО-^СЧЮ-Н
шн
ООО
82 со —¦
d г
Si
I I1° 11
№11111
оо
| N |
N | N | N |
N N N | N | N |
N | N | N |
N | LO | ю |
со | СО | со | со N |
| о |
о | о | о |
ООО | 0 | О | О | О | О | О | о | о | о | о | о | оо |
| ш | щ | ш |
ш | WWW | W |
ш | Щ |
Ш | ш |
Ш | ш | Щ | щ | щ | Щ | WW |
| оз |
ОО | w—i |
СО | 00 см со | со | СО | см |
со | со | Оз |
lO | ю | со |
сч | см | CM lO |
| ю | чО | см СОСО | со | со | О | N | N | 03 | см | со |
ОО | СМ N | ||||
|
СО | ю | ю |
СО cf 04 |
О | СО | ОО |
iO | со | со | оо | тГ< |
со о | ||||
| см |
см | см | см |
см сч см | см |
СМ | см | 03 | ю | ю | со —¦ | |||||
| о | о | о | о | odd | о | о | о | О | о | о | о | о | о | d | о | г г |
¦ ISNNb-I'->00000
шишии
3 N N со Tf 3)SNI0(N<N - чО со N CN CN ^ со со ^ m\G
I I : I I I I I I I I I
NN t4 i ООО *
шищ
мою!
СМ -ч —t
^ Ю ю to W ю
|
СО | СО | СО |
со | со | СО |
| о | о |
о | о | о |
о |
| ш |
ш | ш |
щ | ш | щ |
| 03 | 03 | 03 | см | см |
см |
| ОО N | СО N | ОО ОО | ю со со |
iO СО со | |
| о | о | о | о | d | о |
Hf ь
25s
ю=Е
к о
1ШШ
1 03 Оз * ^03
> СО -Ф
> со со
I I I
ООО
ЗЮЮЮЮЮ^СМСМГГ—«-^CMCOtO^ONN >OOOOoOOO°OOOQOOQQ
1 1 1T 11 TT;
ЩШИЩШИЩЩШИИЩЩШЩЩЙ OQCNNM3)-h«UJ03 03iOlOiO-hOO CO'-So0303NC^C^03C0c0N0)03-HC0c0 C0C0O0303C00000N<N<NNC0C0rr'Tf4^ ОЗЛРЗ-Н-Н-НЬЬ-НСЧС^Т^-Н-ЧСОСОСО
OO I 00
iO О О Ю О О iO О О lO о о ю о о 10 о о о О Ю О О^оО о о 0-н00—«00-ч00—«00—«00-^00—«ОО^ОО*—00—*0
^3 р ° 03 к5.
OO'-<^'4CqW(NC0c0C0'4j'^^l0i0i0CD«0c0NNr'00 00c0(?5050)O
Продолжи vi v\ ft
О ~
§15
4S
О О
с. о.
Со
е
КЗ
ОЙЯ 0.0 о «S
С О
о о,
u с
о
к *
ра
I-
с
еГ ь
2®s “ 2 • ю я»г
К
I- Ж
«
s
? о О го
<N СЯ СО <М *Л
ттт?т
ШЦЩИШ сО СО t'- t'- —' i^-. со qd •*¦» to
<NOO-DO
t4^ со со *-« со
i i f Г®
SNNN N О О О О О
со ос? ООО lONhNN Ю Ю Ю Ю Ю ЮЮ1ЙЮЮ
ЙШИШИ
ю LO со to 00 cOcO LO to
?« OiCi 88
ООО |*0
ШЩЩЦШ
Q-^^OOO)
*o о о <o о 00 ^ ^ Tf СО
•4<NW<0-^
05 OO^Nrf
1Т7ТТ
ЩШРЗШЩ
со —< *—• ¦**-> со ю — -н<мо тг со со оо ^
Ю О о ю о 0~ ОО—i
gCJ <N CO ^
rf> cO <!7> >0 СЧ
х
сз
«
S 2 н I
’S Гт1
s <?
S5 см »-*
О
к ^ Й ю § 10
щ ш J<Kl<to
V** <41 /VI
§NS3 S? 2
!> W <tO
CD
<<о
nS
СП
о
»к
о
я
л
n;
00
о
Ш
ex
»х
о
к
о
к
г
с
сх
с
| МПа |
сосососососососососо оооооооооо |
| еа & С О 1—1 | сосососососососососо COCO<OtO<OtO<OCOtOtO сосососососососососо оооооооооо |
| с3 С ? сч СХ С о |
СОСОСОСОСОСОСОСОСОСО оооооооооо шшщшшшшшсши 0000<N^<N^^«0 ОООООООООО |
| го С ? |
сосососососососососо оооооооооо |
| и сх с: Сэ U-I | ЩЦШШШЩЦШЩШ сосососососососососо tOcOvOCOcOvOtOcDtOCO сосососососососососо оооооооооо |
| Я С S н р. с Ъ |
сосососососососососо оооооооооо щщшшщщщщсиш ОСОСЛО^Г-.СООСОСОСО сосососососососососо оооооооооо |
| Я |
ОСОО^ОСОЮЮЮСОСО оооооооооо |
| К ¦в- о *=t |
шшщшшшшшши CD-iT}iL0O0)O'Hl^L'5 СПСО^^—<GOoSlC3C^CD <Na5CS|C^CDtO^Ot^COrO «-.¦^^сОЮиОС^-ч-ч Г \ \ \ Г1 iood |
| S н сз И я *=[ сх о о | оюооюоо^ооо 00—100-^00^0 |
| Номер участка |
СОСОСОСОСОСО'^'^'^Ю |
Номер
участка
% !¦ «Па
КР2] мпа
о
5
6 6 6 7 7
7
8 8 8 9 9 9
J0
10
10
И
11
И
12
12
12
13
13
13
14 14
14
15 15
0.139Е
0.145Е
0.145Е
0.146Е
0.150Е
0.150Е
0 J47E
0 147Е
0.147Е
0.140Е
0.135Е
0.129Е
0.152Е
0.141Е
0.172Е
0.136Е
0.132Е
0./31Е
0.156Е
0.193Е
0.192Е
0.206Е
0.231Е
0.230Е
0.230Е
0.240Е
0.240Е
0.222Е
0.212Е
0.157Е
0.116Е
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
0.363Е
0.363Е
0.363Е
О.ЗбЗЕ
0.363Е
О.ЗбЗЕ
О 363Е
0.363Е
О.ЗбЗЕ
О.ЗбЗЕ
О 363Е
0.363Е
0.363Е
0.363Е
0.363Е
О 363Е
0.363Е
0.363Е
0.363Е
0.363Е
О.ЗбЗЕ
0.363Е
0.363Е
0.363Е
0.363Е
О.ЗбЗЕ
0.363Е
О.ЗбЗЕ
0.363Е
0.363Е
0.363Е
О.ЗбЗЕ
0.363Е
0.363Е
0.363Е
0.363Е
О.ЗбЗЕ
0.363Е
0.363Е
О.ЗбЗЕ
0.363Е
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
0.148Е
0.148Е
0.148Е
0.148Е
0.148Е
0.148Е
0.148Е
О.ЗбЗЕ
0.363К
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
Координаты
М
деф’
Н м
| 0.5 |
0.1913Е | 06 |
|
1.0 | 0.2756Е | 06 |
| 0.0 | 0.2756Е |
06 |
| 0.5 |
0.2955Е | 06 |
|
1 0 | 0 3498Е | 06 |
| 0.0 | 0.3498Е |
06 |
| 0.5 |
0.3224Е | 06 |
|
1.0 | О.ЗЗОЗЕ | 06 |
| 0.0 | 0.3303Е |
06 |
| 0.5 |
0.2367Е | 06 |
|
1.0 | 0.172ЭЕ | 06 |
| 0.0 | 0.1728Е |
06 |
| 0.5 |
0.1303Е | 07 |
|
1.0 | 0.8581Е | 06 |
| 0.0 | 0.8586Е |
Об |
| 0.5 |
0 3451Е | 06 |
|
1.0 | — 3005Е | 06 |
| 0 0 | — 3005Е |
06 |
| 0.5 |
—.6698Е | Об |
|
1.0 | —.1193Е | 07 |
| 0.0 | —.1193Е |
07 |
| 0.5 |
¦—.HOI Е | 07 |
|
1.0 | —-. 1761Е | 07 |
| 00 | —¦. 1762Е | 07 |
| 0.5 |
—¦ .1763Е | 07 |
|
I 0 | —Л904Е | 07 |
| 0.0 | —Л904Е |
07 |
| 0.5 |
—. 1651Е | 07 |
| 1 0 | —Л521Е | 07 |
| 0,0 | —. 1519Е | 07 |
| 0.5 |
0.3544Е | Об |
1°пр il>
|
МПа | °пр 2* | МПа |
| 03 | 0 112Е |
03 |
| 03 | 0 106Е | 03 |
| 03 | 0 106Е | 03 |
| 03 | 0 104Е | 03 |
| 03 | 0.100Е |
03 |
| 03 |
0.100Е | 03 |
|
03 | 0.102Е | 03 |
| 03 | 0.101Е |
03 |
| 03 | 0 101Е | 03 |
| 03 | 0.107Е | 03 |
| 03 | Q.1UE | 03 |
| 03 | 0.118Е |
03 |
| 03 |
0.642Е | 02 |
|
03 | 0.838Е | 02 |
| 03 | 0.513Е |
02 |
| 03 |
0.874Е | 02 |
|
03 | 0.905Е | 02 |
| 03 | 0.889Е |
02 |
| 03 |
0.623Е | 02 |
|
03 | 0 250 Е | 02 |
| 03 | 0.237Е |
02 |
| 03 |
0.868Е | 01 |
|
03 | —Л70Е | 02 |
| 03 | —.J77E |
02 |
| 03 | — .182Е | 02 |
| 03 | —,285Е | 02 |
| 03 | — .283Е | 02 |
| 03 | — Л10Е | 02 |
| 03 |
— .230 Е | 01 |
|
03 | 0 548Е | 02 |
| 03 | 0.921Е |
02 |
Продолжение
МПа
МПа
МПа
nps’
Номер
участка
'пр 1
Координаты
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О 363Е
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
о зезЕ
О.ЗбЗЕ
02
02
02
02
02
02
02
02
02
02
02
02
02
02
02
02
02
02
02
02
02
02
02
02
02
02
02
02
02
02
02
0.646Е
0.646Е
0.583Е
0.607Е
0.607Е
О 674Е
0.745Е
0.745Е
0.802Е
0,900 Е
0.891Е
0.887Е
0.683Е
0.76SE
0.790 К
0.766Е
О 657 Е
0.846Е
0.794Е
0.817Е
0.740Е
О 793 Е
0.783Е
О 746Е
0.594Е
0.688Е
0.699Е
0.669Е
0.573Е
Q.689E
0.700Е
0.139Е
0.139Е
0.142Е
0.136Е
0.136Е
0.124Е
О 1I2E
0.112Е
0.103Е
0.916Е
0.925Е
0.901 Е
0.107Е
0.974Е
0.954Е
0.964Е
0.107Е
0.856Е
0.880Е
0.857Е
0.898Е
0.8UE
О 820Е
0.830Е
0.955Е
0.861Е
0.833Е
0.845Е
0.942Е
0.792Е
0.747Е
сл
| 15 | 1 0 |
|
16 | 0.0 |
| 16 | 0.5 |
| 16 |
1.0 |
| 17 | 0.0 |
| 17 | 0.5 |
| 17 | 1 0 |
| 18 | 0.0 |
|
18 | 0.5 |
| 18 | 1 0 |
| 19 |
0.0 |
| 19 | 0.5 |
| 19 | 1.0 |
| 20 | 0.0 |
| 20 | 0.5 |
|
20 | 1 0 |
| 21 | 0.0 |
| 21 |
0.5 |
| 21 | 1.0 |
| 22 | 0.0 |
| 22 | 0.5 |
| 22 | 1.0 |
|
23 | 0.0 |
| 23 | 0.5 |
| 23 |
1.0 |
| 24 |
00 |
| 24 | 0.5 |
| 24 | 1.0 |
| 25 | 0.0 |
|
25 | 0.5 |
| 25 | 1.0 |
деф
Н м
| 0.1108Е | 07 |
|
0.1109Е | 07 |
|
0.1243Е | 07 |
| 0 1120Е | 07 |
| 0 1120Е | 07 |
|
0.35I0E | 06 |
|
0.5553Е | 06 |
|
0.5552Е | 06 |
|
0.3510Е | 06 |
|
0.2374Е | 05 |
|
0.2374Е | 05 |
| 0 9832Е | 04 |
| — 2791Е | 06 |
|
—.279IE | 06 |
|
—.2432Е | Об |
|
—.2943Е | Об |
|
—.2943Е | 06 |
|
—.7271Е | 04 |
|
—.6046Е | 05 |
|
—.6046Е | 05 |
|
0.2336Е | Об |
|
—.2597Е | 05 |
|
—.2597Е | 05 |
|
0.5973Е | 05 |
|
—.2558Е | 06 |
|
—.2556Е | 06 |
|
— .1988Е | Об |
|
—.2615Е | 06 |
|
—.2615Е | 06 |
|
0.7280Е | 05 |
|
—.3282Е | 05 |
м
| 03 | О.ЗбЗЕ | 03 |
| 03 |
О.ЗбЗЕ | 03 |
|
03 | 0 ЗбЗЕ | 03 |
| 03 | О.ЗбЗЕ |
03 |
| 03 |
О.ЗбЗЕ | 03 |
|
03 | О.ЗбЗЕ | 03 |
| 03 | О.ЗбЗЕ |
03 |
| 03 | 0 .ЗбЗЕ | 03 |
| 03 | О.ЗбЗЕ | 03 |
| 02 | О.ЗбЗЕ |
03 |
| 02 |
О.ЗбЗЕ | 03 |
|
02 | О.ЗбЗЕ | 03 |
| 03 | О.ЗбЗЕ |
03 |
| 02 |
О.ЗбЗЕ | 03 |
|
02 | О.ЗбЗЕ | 03 |
| 02 | О.ЗбЗЕ |
02 |
| 03 |
О.ЗбЗЕ | 03 |
|
02 | О.ЗбЗЕ | 03 |
| 02 | О.ЗбЗЕ |
03 |
| 02 |
О.ЗбЗЕ | 03 |
|
02 | 0 ЗбЗЕ | 03 |
| 02 | 0 ЗбЗЕ |
03 |
| 02 |
О.ЗбЗЕ | 03 |
|
02 | О.ЗбЗЕ | 03 |
| 02 | О.ЗбЗЕ | 03 |
| 02 |
О.ЗбЗЕ | 03 |
|
02 | О.ЗбЗЕ | 03 |
| 02 | О.ЗбЗЕ |
03 |
| 02 |
О.ЗбЗЕ | 03 |
|
02 | О.ЗбЗЕ | 03 |
| 02 | О.ЗбЗЕ |
03 |
L°np i^’
Номер
участка

26
26
26
27
27
27
28 28 28 29 29
29
30 30
30
31 31
31
32 32
32
33 33
33
34 34
34
35 35 35
0.0 0.5 1.0 0.0 0.5 1 0 0.0 0.5 1.0 0.0 0.5 1.0 0.0 0.5 1.0 0.0 0.5 1 0 00 0.5 1.0 0.0 0.5 1.0 0.0 0.5 1.0 0.0 0.5 1.0
05
06 06 06 06 06 06 06 06 06 06 06 06 06 06 06 06 06 06 06 03 06 05 05
05
06 05
05
06 06
02
02
02
02
02
03
02
02
02
03
02
02
02
02
02
02
02
02
02
02
02
02
02
02
02
02
02
02
02
02
03 03 03 03 03 03 03 03 03 03 03 03 03 03 03 03 03 03 03 03 03 03 03 03 03 03 03 03 03 01
02 02 02 02 02 02 02 02 02 01 02 02 02 02 02 02 02 02 02 02 02 02 02 02 02 02 02 02 02 01
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
—.3282Е 0.2588Е —-1748Е — 1748Е —. 1957Е —.7318Е —.7318Е —.7072Е —.7809Е —.7809Е —.1360Е 0.4604Е 0.4604Е 0.1526Е 0.3946Е 0.3946Е 0.1059Е 0.4746Е 0.4746Е 0.3615Е 0.4358Е 0.4362Е —.7810Е 0.3828Е 0.3828Е —.4498Е 0.2716Е 0.2716Е —-1053Е 0.4537Е
0.735Е
0.790Е
0 741Е
О 805Е
О 802Е
О 116Е
0.893Е
0.876Е
0.893Е
0.118Е
0.708Е
0.921Е
0.751Е
0.625Е
0.686Е
О 832Е
0.611Е
0.854Е
0.679Е
0.632Е
0.648Е
0.810Е
0.543Е
0.502Е
0.488Е
0.610Е
0.451 Е
0.460Е
0.502Е
0.734Е
О 363Е
0.363Е
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
0.363Е
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
0.713Е
0.615Е
0.623Е
0.558Е
0.526Е
0.131Е
Q.400E
0.399Е
0.366Е
О 790Е
0.5I6E
0.271Е
0.440Е
0.522Е
0.402Е
0.275Е
0.461Е
0.184Е
0.358Е
0.388Е
0.354Е
0.194Е
0.433Е
0.448Е
0.462Е
0.306Е
0.432Е
0.422Е
О.ЗбЗЕ
О 943Е
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
0 363Е
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
0-363Е
ОЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
О.ЗбЗЕ
Продолжение
| Номер участка |
Координаты | мдеф. Н | м | стпр 1' |
МПа | [°пр 1^’ |
МПа | °лр г' |
'1Па | t°np *1' | ПИ а |
| 36 | 0.0 |
0.4537Е | Об |
0.567Е | 02 | О.ЗбЗЕ | 03 | 0.260Е |
02 | О.ЗбЗЕ | 03 |
| 36 | 0.5 |
0.3632Е | 06 | 0.529Е | 02 | О.ЗбЗЕ |
03 | 0.284Е | 02 |
О.ЗбЗЕ | 03 |
|
36 | 1.0 | 0.4631 Е | 06 | 0.556Е |
02 | О.ЗбЗЕ | 03 |
0.243Е | 02 |
0.363Е | 03 |
|
37 | 0.0 | 0.4631 Е |
06 | 0.727Е | 02 | О.ЗбЗЕ | 03 |
0.738Е | 01 | О.ЗбЗЕ | 03 |
| 37 |
0.5 | —.1095Е | 06 | 0.464Е | 02 |
О.ЗбЗЕ | 03 | 0.309Е | 02 | О.ЗбЗЕ |
03 |
| 37 | 1.0 | 0.2376Е | 05 |
0.390Е | 02 | О.ЗбЗЕ | 03 | 0.356Е |
02 | О.ЗбЗЕ | 03 |
| 38 | 0.0 |
0.2375Е | 05 | 0.381Е | 02 | О.ЗбЗЕ |
03 | 0 365Е | 02 |
О.ЗбЗЕ | 03 |
|
38 | 0.5 | —.5189Е | 06 | 0.531Е |
02 | О.ЗбЗЕ | 03 |
0.181Е | 02 |
О.ЗбЗЕ | 03 |
|
38 | 1.0 | 0.3949Е |
05 | 0.353Е | 02 | О.ЗбЗЕ | 03 |
0.326Е | 02 | О.ЗбЗЕ | 03 |
| 39 |
0.0 | 0.3950Е | 05 |
0.367Е | 02 |
О.ЗбЗЕ | 03 | 0.311Е | 02 | О.ЗбЗЕ |
03 |
| 39 | 0.5 | —.6554Е | 05 |
0.372Е | 02 | О.ЗбЗЕ | 03 | 0.279Е |
02 | ОЗбЗЕ | 03 |
| 39 | 1 0 |
0.6310Е | 06 | 0.758Е | 02 | 0 363Е |
03 | —.132Е | 02 |
0.148Е | 03 |
|
40 | 0.0 | О.бЗЮЕ | 06 | 0.524Е |
02 | О.ЗбЗЕ | 03 |
0.990Е | 01 |
О.ЗбЗЕ | 03 |
|
40 | 0.5 | 0.5757Е |
Об | 0.499Е | 02 | О.ЗбЗЕ | 03 |
0 110Е | 02 | О.ЗбЗЕ | 03 |
| 40 |
1.0 | 0.7367Е | Об | 0.546Е | 02 |
О.ЗбЗЕ | 03 | 0.495Е | 01 | О.ЗбЗЕ |
03 |
| 41 | 0.0 | 0.7367Е | 06 |
0.818Е | 02 | О.ЗбЗЕ | 03 | —.221Е |
02 | 0-148Е | 03 |
| 41 | 0.5 |
0.I929E | Об | 0.420Е | 02 | О.ЗбЗЕ |
03 | 0.148Е | 02 |
О.ЗбЗЕ | 03 |
|
41 | 1.0 | 0.3745Е |
Об | 0.535Е | 02 | О.ЗбЗЕ | 03 |
0.711Е | 00 | О.ЗбЗЕ | 03 |
| 42 |
0.0 | 0.3745Е | 06 |
0.398Е | 02 |
О.ЗбЗЕ | 03 | 0.145Е | 02 | О.ЗбЗЕ |
03 |
| 42 | 0.5 | — .2799 Е | 06 |
0.354Е | 02 | О.ЗбЗЕ | 03 | 0.165Е |
02 | О.ЗбЗЕ | 03 |
| 42 | 1.0 |
—.6297Е | 06 | 0.461 Е | 02 | О.ЗбЗЕ |
03 | 0.365Е | 01 |
О.ЗбЗЕ | 03 |
|
43 | 0.0 | — .6296Е | 06 | 0.461Е |
02 | О.ЗбЗЕ | 03 |
0.365Е | 01 |
О.ЗбЗЕ | 03 |
|
43 | 0.5 | — .7724Е | 06 | 0.494Е |
02 | О.ЗбЗЕ | 03 |
—.272Е | 01 | 0 148Е | 03 |
| 43 | 1 0 | —.7001Е |
06 | 0.454Е | 02 |
О.ЗбЗЕ | 03 |
—.179Е | 01 | 0.I48E | 03 |
| 44 |
0.0 | —.700 iE | 06 | 0.454Е | 02 |
О.ЗбЗЕ | 03 | —.179Е | 01 | 0 148Е |
03 |
| 44 | 0.5 | —.3595Е | 06 |
0.307Е | 02 | О.ЗбЗЕ | 03 | 0.650Е |
01 | О.ЗбЗЕ | 03 |
| 44 | 1.0 |
— .9625Е | 05 | 0.189Е | 02 | О.ЗбЗЕ |
03 | 0.124Е | 02 |
О.ЗбЗЕ | 03 |
|
45 | 0.0 | —.9625Е | 05 | 0.189Е |
02 | О.ЗбЗЕ | 03 |
0.124Е | 02 |
О.ЗбЗЕ | 03 |
|
45 | 0.5 | 0.3090Е |
05 | 0.117Е | 02 | О.ЗбЗЕ | 03 |
0.970Е | 01 | О.ЗбЗЕ | 03 |
| 45 |
1.0 | 0.2058Е | 05 |
0.708Е | 01 |
О.ЗбЗЕ | 03 | 0.569Е | 01 | О.ЗбЗЕ |
03 |
1
Продолжение
| СО | со |
СО | сО | со | со | со |
со | СО | со |
со | со | со | со | со |
со | со | со |
| О | о |
О | О | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о |
| Ш | Ш | ш | ид | W | ш | ш |
ш | ш | ш |
ш | щ | ш |
ш | ш | ш |
щ | ш |
|
со | оо | оо |
СО | оо | СО | со | СО |
ОС | со | оо |
00 | со | со | оо | 00 |
О0 | оо |
| ю | >*• | чг | ч* |
||||||||||||||
| со | *—‘ |
¦"Ч | *“2 | —« | *—* | “1 | м_ |
||||||||||
| о | О | О | О | о | о | d> |
о | о | о |
о | о | о |
о | о | о |
о" | о |
С
?
Си
С
| о | о | см о | см о | см о | о |
сч о | сч о |
сч о | сч о |
см о | СЧ о | сч о | сч о | сч о | сч о | сч о | сч о |
| щ о> S | .450Е | .125Е |
ы ю см | Uj о со | ш 00 сч |
.428Е | .554Е | .608Е | ы 00 8 | W 2 | ш сч П* <о | W сч СО |
.647Е | ш о> TJ- со | •649Е | .650Е | .650Е |
( ( <
М ! II II II
| со |
со | СО | со | со | со |
со | со | со |
со | со | со | со | ?2 |
со | СО | со |
со |
| о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о |
| ш | ш | ш | ш | ил | ш |
ш | ИД |
щ | ид | ид | ид | ид |
ид | ид | U-) | ид | ti3 |
| со | 00 |
СО | со |
оо | со |
ОО | со |
оо | СО | 00 | со | 00 |
со | со |
со | ОО |
со |
| со |
*«а< | ГГ | |||||||||||||||
| со | 1—* |
«—« |
*¦—* | »—4 | «—<1 | •** |
¦—* | **] | “• | ||||||||
| о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о |
и
?
00 о Ю Ю 05
| сч | сч | Сч |
| о |
о | о |
|
ил | щ | Ш |
| СО | 00 | |
| сч | сч |
1ГЭ |
| tQ |
<м
о
W Й И
со оо с*
|
сч | сч | сч |
сч | сч | сч |
| о | о |
о | о | о |
о |
| ид | щ | ид | ш |
ид | щ |
| см | сч | г- тГ |
С7> 2 | сл |
S3 |
| CD |
со | со | со |
со |
о
с
?
ООО
о
(X
а
о
Вывод:
1. Конструкция удовлетворяет условиям по деформации
I I I N I м I I м I м I I
cs N N СО tD
{s. СО п Ф Is-
00 00 СО СЛ г-
Г-. Csl см ^ —
6 j* Г Г о
| со | ю |
Г-- | г- | 05 |
о |
| о 1 |
т | о 1 |
? | 7 | |
|
ид | Щ | / щ | щ | f W |
ш |
| со |
О) | 05 | со |
||
| N |
с» | о> | to |
со | |
| г- |
ю | Ю | ю |
г- | <м |
| со | со | со | -ф | со | |
| о | о |
о | о | 1 |
|
о | сч | |
|
т | т | 1 |
| 1 ш | 1 ш | 1 ш |
| 1^ | 05 | |
| со | ю | <х> |
| о^ | со | о |
| со f' | 00 о* | 1 |
to
о О ш ы
00 Ю ю <м
— тр
сч сч о о
о о
S
X
ИД Ш 8 8
00 00 )' Г I'
^ррюорюо
О-'ОО-^ОО—*
Р lO р р 0 0-^0
&
S*
Is
NNCOoOOOOifflffiOOQ^wM
¦^¦^'з,\ст|‘т}'^^Й101йи0ЮЮ
CD СО СО rf" ^ ХГ
РАСЧЕТ УЗЛОВ РАЗВЕТВЛЕНИЙ ПОДЗЕМНЫХ ТРУБОПРОВОДОВ С ПРИМЕНЕНИЕМ ЭВМ
Под узлом азветвления подземного трубопровода понимается система, сое оящая из прямых участков трубопр вода и со динительных деталей. Тамге конструктивные схемы применяются при проектировании крановых обпязок, шлейфов, подходов трубопроводов к ыногониточным переходам, подземных обвязок компрессорны станций и др.
При воздействии температурного перепада и внутреннего давления рассчитываемая конструкция трубопровода, включающая соединительные детали, испытывает ие только радиальные нагрузки от внутреннего давления, но и ус алия и изгибающие момента от перемещения всей системы. Усилия и из нбающие моменты в существенной мере зависят от конфигурации системы, взаимодействия трубопровода с грунтом и расположения опорных связей.
Опыт эксплуатации трубопроводов показал что для трубопроводов больших диаметров (свыше Г00 мм) напряжения иродольно-поперечного изгиба значительны и могут привести к отказам системы. В связи с этим нормы иа проектирование магистральных трубопроводов требуют проверки прочности тройииковых соединений на воздействие не только внутреннего давления, но и изгибающего момента и продольных снл.
Расчетная схема подземного трубопровода с узлами разветвлений является достаточно сложной. Система состоит из ряда конечных и полубеско-н< чных по длине участков трубопровода, криволинейных вставок различной есткости при этом характеристики грунта, нагрузки и воздействия могут ыть различными по участкам. Все это обусловило применение численных етодов расчета и привлечение ЭВМ для их реализации.
§ 1. Область применения программы «Узлы-78»
Программа «Узлы-78», разработанная ВНИИСТом и ЮжНИИГипрога-зом, позволяет рассчитывать плоскую систему трубопровода произвольной конфигурации, состоящую из прямолиней (ых, криволинейных участков (ул-р>го-изогнутых или отводов) трубопроводов. В местах разветвления трубопроводы соединены между собой тройниками. В качестве нагрузок н воздействий рассматриваются внутреннее давление продукта температурный перепад н внешние сосредоточенные усилия (продольная и поперечная енлы н изгибающий мрмеят). Внутреннее давление н температурный перепад могут Сыть различными по участкам трубопровода, сосредоточенные усилия могут быть приложены в любом сечении по длине рассчитываемой конструкции. Граничные условия рассчитываемой системы могут быть произвольными и задаются характеристиками жесткостей примыкающих конструкций. В произвольных сечениях рассчитываемой системы могут быть упругие связи, пре-1ятствуюЩ1е продольным, поперечным и угловым перемещениям. Программа <0> злы-78» написана на алгоритмическом языке Фортран-IV для ЭВМ ЕС любого типа. (Текст программы иа машинных носителях хранится в органи-зациях-разработчиках). Для практических расчетов создана форма подго товки исходных данных.
Для определения иапряженно-деформированного состояния узлов разветвления подземных трубопроводов используется численный метод, являющийся разновидностью метода конечных элементов. Исслед; емая конструкция заменяется некоторым числом дискретных элементов, которые затем стыкуются в узловых точках. Выбор числа дискретных элементов определяется геометрией рассчитываемой системы, характером взаимодействия трубопровода с грунтом, а также зависит от конфигурации (объема оперативной
памяти) ЭВМ. В качестве конечного элемента принимается стержень (бал трубчатого сечения, находящийся в среде с двусторонними (продольны* поперечными) связями под воздействием температурного перепада и вА реинего давления Криволинейные участки трубопровода заменяются сов купи стью прямых, являющихся хордами данного сектора. Материал трД принимается упругим. При определении деформаций трубопровода вается двухосное напряженио-деформнрованное состояние напорного труж провода на основе обобщенного закона Гука.
Зависимости сопротивления грунта от перемещения трубы характеризу
и идеализированными диаграммами, состоящими нз ряда прямолине^Г отрезков. Для продольных (вдоль оси трубы) перемещений принята моЛ типа диаграммы Праидтля, для поперечных (перпендикулярно оси рубы) j ремещекии принята трилинейная модель.
На первом этапе расчета принимается, что модель грунта линейная, а пк дольное усилие известно, После определения начальных параметров форм руется матрица системы уравнений равновесия всех узлов, ее порядок рам утроенному числу узлов в рассчитываемой трубопроводной системе.
На основании решения системы линейных уравнений определяются уШ вые перемещения и начальные параметры. Используя уравнения измени перемещений по длине, определяются характерные перемеще! ия и параметр самокомпенсации системы. По найденным величинам определяются иоЛ параметры, характеризующие взаимодействие трубопровода с грунтом и цГ дольные усилия в характерных сечениях. Затем, используя новые параметры, вновь выполняется расчет линеаризированной расчетной схемы. Число -и^ раций определяется иа основе записанных условий сходимости процеГ
Получив параметры взаимодействия трубопровода с грунтом иа послёд нем этапе итерационного процесса, а также- эквивалентное продольное ус* лне с учетом перемещений трубопровода, определяем значения осевых и п~ перечных условий, изгибающих моментов и перемещений для любого и! ходимого сечения рассчитываемого участка трубопровода.
Таким образом, алгоритм прга раммы «Узлы-78» учитывает нелинейное^ продольных и поперечных связей, геометрическую нелинейность (продольН поперечный изгиб) и нелинейность связи между деформациями и переИ щениями.
§ 2. Матрица жесткости элемента
Как отмечалось рапее, каждый элемент на каждом этапе счета рассма ривается как упругий стержень, взаимодействующий со средой, имеющей линейные связи. При получении матрицы жесткости можно пренебречь вли' нием изгиба на продольные перемещения, а продольное осевое усилие п{? иять постоянным по длине элемента. Используя эти допущения, уравиед равповссия в поперечных перемещениях можно записать в следующем видЯ
где Elij — изгибн&я жесткость; — осевое продольное усилие; &ijf« =cy(ij)DE(ij) — произведение коэффициента нормального сопротивления rpyivfl и наружного диаметра трубы- i, / — номер начала и конца элемента.
Запишем решение уравнения (8.1), используя начальные параметры» прогиб v0, угол поворота фо, изгибающий момент М0) поперечную силу Qo Я зависимости М0= ~EIv0"; Q0<=EIv0'" — Sv^f. Здесь под Q0 понимается nonejf ная сила, направленная перпендикулярно к недеформированной оси стержг# Уравнения прогибов, углов поворота, изгибающих моментов и поперечных сн имеют вид:
Mt an = MoRic (if) + Mfln vn QoRi2 a,-) + Qt# 13 «/>;
Q| (if) = Л^и (У) + Ml^lS (if) + Co^.6 (fy) @11^17 (if) » (8-2)
где Rко)- Rmu) — функции безразмерной координаты сечения элемента-
D Vij s*n Vijtijl — f*,7 sin \f%
К1 «Д -¦
COS Pijhfi C0S Vf/g .
*2 (f/> -
4 ~ rii
л,
4 rii
4sin Mi/^-vf/Sinv^g _
^7 0/)
vi? - I*»
'8 (f/) 2 2
(4sin vali? - 4sin fVi/?) .
^7 (if) t ^ ^9 (If) (*) ~ ^8 (if) 0) ^8 (if) ( )
R — ^9 ap R7 (if) (?) ~ ^8 (I Д (1) ^8 (//) (I)
^7 (i/) (0 ^9 (t/) (*) ~*8(if) (*) ^8ОД ^12 (i/) ^3(//)^)“
№«ft W ^e«ft f1) — Ri(ij) 0) ^8(?/) (l)] ^7 (I/)
^14(i/) — ^6 (if)(&“-
[^5(«fl (0 — ^8(ij) (l)] Rfi{ll) Ш t
_ + 1*6 (if) 0) ^7(ij) ~~ ^5(i/) (*) ^8(if) (01 ^9(i'/) (S) .
*7 (tf) 0) *9 (if) (V *8 (if) 0) *8(if) 0)
Д _ *9 W) ^8((7) (?) ~~ ^8 (if) *9(if) (5)
15(,7) «7(4, 0) *9«Л (!) *8ОД (1) *8 ил W ;
*16 (if)" *4 (if) {%) —
[^8(1/1 W ^9(1/1 0) ~ ^4<ij) (*)J ^8(i/) (1)] ^8 (if) ®
__t^4(ffl 0)^7 (i/) (*) *3(1/, 0) *8 (if) (1)1 *9 (if) (S) .
*7 (if) 0) *9 (if) (I) *8 (if) (*) *8 (if) 0)
Вспомогательные функции Тщ» — T\nii), входящие в (8.4), вычисли по формулам:
Т ~ ац Ch аЧ'1чЬ sin hi sh «ijlj/Ъ cos fiijlifl.
T2Uf) ~
_ ад ch ац1цЪ sin $ц1дЪ f>(< sh «,//'?,? cos fly/f/g .
2«c;Pci
(Pi/ - «?/) ?h аЧ1Фsin Р.7г»Д + 2a./P./ ch aHlificos Pi/*i/S . "ф5S* ’
n, (®?/ +Pi/) 5Ьа(^Д5трг/.1?Д-}-2а;;РуСЬа^гДсочРу^
Н/ + Pi/) (Pi/ cosРц1Ф - aij ch VifS sin Pi/*i/?) .
Pi/ (®ai/ ~ Pi/) ®i/*i/5 cosPi/i;S “ a// (3?i; “ aV) *
X ch ац1ф Sin р,../у|
y7(i/) --
2ai/P i/
(«?/ + P?/)2 sh V«* sin Мч* . i* ¦
(ai/ + Pi/) [Pi/ (Py ~ 3c?tj sh cos +
+ a>; (4 - 3P</)ch ai№ sin РЛ-6]
¦
T10 (If) - TS(ij) <&> —
[T7(if) (*)7 9(if) f1) — ^6 (If) 0) T8 (if) I1)] ^7 (if) <S) +
+ 0) Tllto О - ТЧЪ (‘) r8(ifl (01 7 Si/® .
7’7(i/)(‘)7'9(id(0-7’8(i/)(l)r8W(l)
т — ^t</)Q7,7(<7)^~r8(i/)0)7’8(i/)( I) .
^7 (i/) f1) 79(i/) U) — 78 (i/) T8 (ID (l)
TI2(i/) ^T3(lj) Ш —
[ зил (О (О ^4«/) 0) 78 (if) (*)] T7 (ifl №)
__[y4(i/) ^Vtf/) (*) ~ r3(i/) 7 8 UP W] TH (if) fe) .
^7 (i/) (О T9 (If) (*) T8(If) (*) 8 (if) W
T T7 (If) WT8 (jf) (I) — Te (If) t1) T1 (If) ^ .
13 m T7m[\)T9Vfi{\)-T„m{l)TbW(l) '
TH(ij\=*:Tb4l)№ —
Fb(If) (») ТЭ«» 0) - r6од (1) г8вд (I)] Тш (I) +
t^6(i/) (*) ^7 (If) (0 Tb(if) T8(ij) ^)1 ^9(if) (?) .
^7 (i/) ^9 (if) 0) — 8 (if) 0) T% (i/) 0)
_ ^9 (ffl 0) TS (If) (?) y8(»f) П) ^9(ffl (S) .
^7(ij) (4 T*m (1) — T’eit/) M ^8(i/) W
[^ЗОД 0) 0) — ^4(?/) (П T8(if) (*)] T6(ij) (6) +
+ [r4(?fl 0) T7 Ш) (*) “ Г3 Ш) 0)
Tlb(ij) — T4(i]) (fc)
T1Vj) W ^9(iy) 0) — ^8 (if) 0) T8(ij) (0 тпЧ){1)Пт(1) T6m(\)T6UD(i)
T? (If) 0) T9 (ij) (0 — T8 (if) (!) ^8 (if) (!)
Как уже отмечалось, в постановке задачи на каждом этапе расчета счи| таем, что сопротивление грунта т* пропорционально продольным переме ниям и*. Обозначим этот коэффициет пропорциональности через с* о, кото-5 рый в дальнейшем будем называть коэффициентом касательного сопроти| ння грунта. Таким образом, принимаем, что
хх = — схоих\ dNx = nDnXxdx. (8.<j
Для элемента, находящегося под воздействием температуры и внутрЯ него давления (двухосное напряженное состояние), уравнение связи межд| деформацией и усилием имеет вид
dux Nx
ЦОкц
' (8.Ц^
+ аД t-
dx
EF
где tix - продольное перемещение; Nx — осевое продольное усилие, полол тельное при растяжении; EF — жесткость сечення при сжатии (растяженнВ а — коэффициент линейного расширения; А/ — температурный перепад, по^Г жнтельный при нагревании-, ц — коэффициент Пуассона; окц—кольцевые н| пряжения от внутреннего давления. Уравнение равновесия в продольных ne-J ремещеннях на основе (8.6) и (8.7) имеет вид
dx2
яРнсха
(8.9)
/г =
EF
Из решения уравнения (8.8) при граничных условиях х -= 0, их = «о» Nx = No
(8.10).
получаем уравнения продольных перемещений и осевых продольных усили выраженных через начальные параметры:
(8.11)
их = Щ ch пх +
sh nx;
N0 — цОкц/7 + O.UEF EFn
Nx — EFnu0 sh fix + (N0 — цсткц/гa&tEF) ch nx — aAtEF + (8.12)'
Ha основании уравнений (8.2), (8.4) и (8.11), (8.12) можно полу «L матрицу жесткости отдельного конечного элемента. Начальные параметру (элементы матрицы) получаются из условий:
вд1 = Л*о при Фо=1. »о = 0, <Р/ — 0, v{ = 0;
а12= — М0 прн — 1. <Ро=-°. 4>f = 0, vt = 0;
| ^22 —' QO |
при | V0—\, |
<Po = °. | = 0, |
vi 0 | |
| ('21 Qo |
при | <Ро= 1. |
i/0 = °. | <Pf |
0, | uj = 0 |
| *11 — Ml | при | Ч>0 — !. | оо — °. | <Рг | = 0, | V[ = 0 |
| ^12 — Mj | при |
Щ = 1. | %> = 0, |
<Pi | = 0, | p/ = 0 |
| /?22 = - Q/ |
при | 1/0=» 1, |
ip0 = 0, | Ф/ | = 0, | ч/ — 0 |
|
62l Qi | при |
f0 —0, | фо= 1. |
Ф/ | 0, | t)/ = 0 |
| O33 = — Л^о | при | Ho — 1. | щ = 0; |
|||
| ^33 ^ |
при | 1/q =* If |
щ — 0. |
s2
У
[J _ ,
Используя этн условия, находим прн -fi^>cyW)D*W)'
(vi/"" Mi/) (v'ysin I1'/7-/ cos V‘/ ~ Sitl V‘/‘7 C°S ^Ч1Ч ;
аП(«д= Qf[-
Mijvij [(f*i/ + v?/)cos Ыч cos V‘7 +
+ 2iyt, sin 1sin viflu — (И?,- + v2 1
al2(lI)-a2Hij) Qf/
(vg - Pi/) К sin V</ cos Mi ~~ Min C0S ViL;
°22((/) “ Qv
(vi; - И-l) Kv sin 5™У>7~) .
bimi)- Qf/
Pkv.v (4 ~ ^ С08^Л/-С03У^ ¦
*12 («й - *21 W) - Qy ~
- Н/ - ^7) К/sin v» *‘/ ~ ^‘75Ш M/L (8 14)
*22 ОД - Q?/
где
Qij
К/ 'I' 4) sin Ht/Af sin V.7 + 2Mt/vf/ (cos М/ C0S V<7 0 (8.15)
?/i/
Для случая —<cyUi>DHUi) аналогично имеем
«i/Рг/ (Pi/sh 2a.uhj — ац sin 2pц1ф_.
0,1 « “ “ ' “оТ-
°12 Uf) ~ c2l (ij) “
««/Plf «¦ + P?/) (Рх/ sh 2V.7 + «V sin2P-7f.v) . в22ад- Q<y.
2ауРг/ (Pf/ sh аг//у cos — а?/ ch ay/y sin рй-/„-)
*. "8 о»-’
2ttf/P,-/ (4-+ft//)sh Vgsin P I f
b12(f/) = fc21 (?/)
%,7pt/ (a^ + Py) (p , sh a?//,y cos Pl7/V 'I a?/ ch <y(| sin pt/y'
"оо /;л —
—--—*———-——-----— —
ш
22 (if)
Qf/
где
Pf/ sh af/f; aij sin Pf/f/
(8-17И
Vff -
Elli
Независимо от относительной жесткости подземного элемента, т. е. cq отношения между Sij/4?/,-,- н
г _ _ рр chn«lU . аэз (if) — писг и . :— »
Sh «у/f/ 1
*33 (ij) = nijEFif
(818)
Sh Лу/у
то nepeni «ЗРОД = + 0,2(ткц(1-й) F?/.
Реакция от давления и температурного перепада (р, Д/) определяется Tio ' формуле
(8.19)
§ 3. Определение усилий и перемещений
Конечным элементом является прямолинейный отрезок трубопровода! жесткость которого и характеристики его взаимодействия со средой одгаиД ковы по длине. Для него также постоянны по длине воздействия — темпера-j турный перепад я внутреннее давление. Граничными точками расчетного учяГ стка трубопровода назовем такне, в которых известны псе компоненты вн^Н них усилий или задана связь с прнмыкающейся конструкцией. К узловым', точкам будем относить также границы конечных элементов и места расп^^И жения опор. Предполагается, что в каждом узле в общем случае стыкует^ три элемента (рис. 43). Узел стыковки / характеризуется тремя примьн^^™ щими точками /, к, т, тогда каждый элемент обозначается двумя нндексаЛЯ С началом отсчета в узле (рпс. 44). Длина элемента — расстояние меДЩ узлами — обозначается буквой с двумя индексами, иапример li}. Полож^Г_ вектора в плоскости описывается углом поворота, образованным вращением вектора по часовой стрелке до совмещений с единичным вектором. В качеств единичного вектора принята ось, направленная условно вертикально bi^T угол обозначается ф*,-. Считается, что в каждом узле возможно действ! внешних сосредоточенных сил—двух составляющих усилий R2, Rs и изги^ бающего момента R\. Положительное направление усилий принято вдаГ осей местной декартовой системы координат, а изгибающего момента—пИ часовой стрелке. В каждом узле имеются три упругие связи, направление (Olf торых совпадает с направлением усилий. Жесткости угловой и линейны* связей, представляющих собой реакцию, вызванную единичным перемещением этих связей, обозначены соответственно Qu q-2 и <7s- Уравнение равновеФЩ для i-го узла с примыкающими элементами 1ц, Uk, Um записывается в виД*|
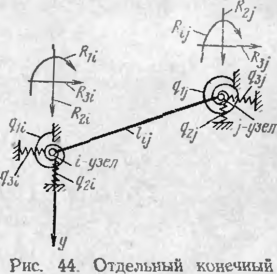
элемент
(«—о ^п-1 Z* ~t” (n+i)Zn+i +
+ ^п(п+2)^п+2 ^ *пР. (8 2 )
Элементы уравнения (8.20):
вектор узловых обобщенных перемеЩе-
2„ =
2/1 + 2 —
'ко
(8.22)
RnP~
| ний | |
| 2?/—2 | |
| л II | Zsl—1 |
| Z:№—2 | |
| —>- | |
| ¦2/1+1 — | %эт—1 |
| %зт |
ISCKTOP грузовых членов
%з1г—2
Z'ik—l Z-.tk
is
Z*1-1
%3i
(8.21)
— R (il—2) P
— Rq(—1)P
^2(i) (30 /> — #3(0
Матрица податливости узла, состоящего из трех элементов:
Г(3?-2) (3/—2) '(Зг-2) (3/-1) /‘(3i-2) (3/)
Г(3г—1) (3/—2) Г(3?-1) (3,-1)
Г(3?—1) (3/)
'п (и—I) :
Гзг (3/-1) Г(30 (3/)
г(30 (3/—2)
|
'(31—2) (3ft—2) | r(3?—2) (3ft—1) | r(3?—2) (3ft) |
| (3?—1) (3ft—1) | r(3i—1) (3ft—I) | r(3?-l) (3ft) |
| r(3() (3ft—2) |
r(3?) (3ft—J) | r(3i) (3ft) |
| r(3C~2) (3m—2) | '(31-2) (3m—I) |
r(3i—2) (3m) |
|
r(3i—J) (3m—2) |
Г(3m-l) |
r(3i—l) (3m) |
|
r(3i) (3m—2) |
f(ii) (3m—1) |
r(3Q (3m) |
|
r(3i—2) (3i—2) | r(3i-2) (3?—I) | r(3i-2) (3?) |
| r(3i— 1) (3i—2) |
r(3(-l) (3?—1) | r(3i—1) (30 |
| r(3f) (3f-2) |
r(3i) (3i—I) |
rW) (3i) |
Rnn -
'л (rt+1)
Исходя из принятых обозначений коэффициенты riS системы канонич ских уравнений и грузовые члены Pip выражаются через элементы магрн жесткости следующим образом:
г(3?—2)(3/—2) — bil (?/)'•
r(3(-2)(3i- 2) — aU(i/) + °и (ik) + °п dm) + яI ([)• (3i—2) (3/-1) = — *12 (if) sin "Pi/I r{3i—2) (31-1) — a12ij s!n %j +
+ al2 (ik) sin V(k + "12 (im) «'Я 4im,
r(3i—2) (3?) = al2(t/) cos 4V/ +
гШ—2) (3j)--612 (if) cos Ч>?/
+ a\2 (ik) C0S Vik + “12 (im) cos %m’
: ^12 (i[) sin 'ti/'
431-1) (3/—-2)
Г(31—1) (3/—I) ~ b22 (if) Sin2 Ч>?/
^33 (?j) cos* 4>|/J
r(3i~ l) (3/) = (~ b22 од + 633 {t-^ sin <р4/ cos ф1у-; i) <3i—2} ~ flIZ (Cj) s*n Vif ~Ъ e12 (ik) sm 44k + «12 (im) sin 4tm'
(3/ J) = «22(//> sin* %! + a22(ik) sin2 %k + a22(tm) s,n® Vim + + Ъ (0 + O33 (i/)cos2 4>i/ + «33 (ik)COs8 Vik + «33 (im) cos* <pto; r(3i-l) (3t) = (“22 (if) — «33 (if)) sin f'il cos + («22 (?ft) “ «33 (i/г)) X x Sin <p,.fe = COS фа + («22 dm) ~ «33 (im)) sin %m C0SГ(3i) (3/—2) bl2 (i/) C0S 'fir
r(;<C) (;</-[) — ( ~ *22 (Cj) +*33 (tj)) sin fijcos Vif
r(3i) (3/) ~ ~~ *22 f//> cosS 4*;/ — b33 (if) Sin* q>if + g3(ij; r(3E) (3i 2) = «11 (I/) cosVil + °11 (ik) cos 4>?fc + 0ц dm) COS <pim;
r(3Q (3i—1) — (°22 (?/) — «33 (if)) sin 4*1/ COS Фу + («22 ((ft) ~
- «33 (ik) Sin %k C0S %k + («522 (im) - «33 (im)) sitl «Pirn COS Vfa|. ff(3i~2)P = 0;
(8 24)
J
Я (з?—1) Р--a3P(lf) С05’Л1/ — аЗР (in) cos Vim ~ а3Р (I*) cos ‘Pit’
R (30 р = °3р ОД sin «Pi/ + °3Р (im) sin Tim + аЗР (№) sinЪк' (8.25)
Под компонентами напряженно-деформированного состояния конструкции понимаются перемещения — линейные и угловые, усилия — продольная сила, поперечная сила и изгибающий момент — и нагрузки на связи — все т )И составляющие. Для определения этих компонентов из решения системы уравнений (8.20) определяется перемещение узловых точек Далее, используя элементы матрицы жесткости определяются граничные параметры каждого конечного элемента. Формулы для вычисления поперечного перемещения, угла поворота, изгибающего момента, поперечной силы и продольного перемещения для начала и конца элемента следующие:
°0 ОД--Z3t~l sin Ф17 Z8i cos Ф?/'
Фо ОД = Zbl-2'
Mo ОД ~ Z(3?-2) ail(lj)— (^87-1^21 (II) S*n ^8;*21 ОД C0S W{j) +
+ ^3/—2*11 (?/) + ^8i-le12 ОД sirl Ф|/ + Zgiai2 (?/) cos 4>f/:
Qo од ~ (?si cos tpy -f- Zi(1 sin «22 од + zsi-2asi (ij)
(ZSi C0S Vl/ + Z3/-l sin *P//) ^22 (?/) + ZMj-2b2l ОД»
«о (y) = ^ gi—icos Фг/ + z8t sin фгу,
= zs/-2°tl ОД + (Za/-1sin % + Z3/C0S Фу) Я22ОД —
— (Zsi cos <рг/ + ZsJSin (ptl) bl2 {ij) — Z6i_?n {i/);
tffl ~(~zalcos Фг/ ~ zs/-isin Ф«/) fl22 у,-) + Z8/~a°22 од +
+ (Z#/ COS q)t/ + Zzi_xsin ф;/) *22 (гл + VaVffl!
Um = Zzi-l C0SЬ/ + ZSi Sin V
(8.26)
Для определения компонентов напряженно-деформированного состояния трубопровода в промежуточных сечениях по длине элемента используются уравнения (8,2) нлн (84), в зависимости от его относительной жесткости, и (8.12). Нагрузка на опоры определяется как разности усилий, действующих в сечениях трубы слева и справа от опоры.
§ 4. Методика учета геометрической и физической нелинейности
При расчете трубопроводов на воздействие температуры в внутреннего давления нелинейные эффекты оказывают значительное влияние на напряги енно-дефор мированное состояние конструкции, поэтому опишем методы учета нелинейностей, реализованные в программе «Узлы-78». Для учета геометрической нелинейности при нахождении матрицы жесткости использовано нелинейное уравнение (8.1), второй член которого отражает изменение геометрии системы в процессе нагружения.
На основании нелинейной связи между деформацией и перемещением получены уравнения, связывающие эквивалентное продольное осевое усилие с перемещением трубопровода
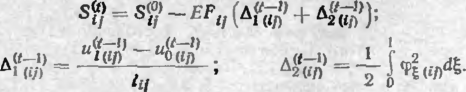
(8.27)
Реализация этих зависимостей осуществляется итерационным методом с нД пользованием значепий перемещений, полученных на предыдущем этаЛ счета (/—1). Для учета физической нелинейности грунта, т е. нелинейности зависимости сопротивления грунта от продольных и поперечных сопропЯ лений, расчетные модели которого описаны в гл. 3, применяется метои| переменных параметров упругости. На каждом этапе счета нслользуедЯ линеаризированная модель грунта, количественные параметры которой опрЗ деляются на основании перемещений, полученных па предыдущем этаД счета. Для определения значений параметров коэффициентов нормального*» касательного сопротивлений грунта используются следующие аналитические зависимости:
(
g» <«/)
при |г,.(0,5)|< —-
«/)
H (if) c\ (if)
^(if)D
н (•/)
при
81 Vi)
(if) , & (if)
T--
(?/) c2(tf)
B2(iD~Si(iD
)•
DK di) CI0»
C3(if)D„(lf)
Dn (ij) c2 (if)
(if) I vif (0.5) |
ua (if) V 4 gl df)
^2 (i/> + ( I (°-5) I--p
V я (if) C1 (?/) /
и df) Cl W)
Dh (If) | vif (°’5) |
при | vcj (0,5) | >
gi (if) cl (.7)
+
(8.28)
1/'
/
лРи(17) cjtQ W)
*np (if)
EFu
nDK (if) Cx0(if)
(8 29)
пц
np (i/)
np (if)
?F0|«i/(0,5)l
nDIl (if) CX0 (ij)
при [| Uij (0,5) | >
при j игу (0,5) |
Критерием остановки итерационного процесса принято условие, при котором относительная разность параметров, определенных на последующем я предыдущем этапах счета, не превышает наперед заданной величины. Эта величина установлена на основе численных экспериментов.
§ 5 Исходные данные для расчета на ЭВМ и выходная информация
Вначале вся рассчитываемая система, состоящая из прямолинейный участков, кривых упругого изгиба, отводов и тройников, разбивается на конечные прямолинейные элементы. Криволинейные участки трубопровода заменяются совокупностью прямых, являющихся хордами сектора Кривые
малого радиуса (отводы) рекомендуется разбивать на одинаковые по длине элементы. Прямолинейные участки трубопроводов также разбиваются на отдельные элементы. Целью разбивки прямолинейных участков на отдельные элементы является более полный учет физической нелинейности грунта. Поэтому на участках, где могут иметь место большие перемещения, длины элементов должны быть меньшими. Длины элементов в местах примыкании к углам поворота рекомендуется принимать равными 5 -10 диаметрам трубы, увеличивая их постепенно по мере удаления от утла. Узловые точки, где сты-ку ются элементы, обязательно назначаются в местах установки тройников, кранов, стыка прямолинейных участков и криволинейных; в сечениях, где приложены внешние сосредоточенные усилия (моменты, поперечная и продольная силы); в топках, в которых имеются связи (опоры); в местах изменения любого из параметров трубопровода диаметра трубы, толщины стенки трубы, температурного перепада, физико механических характсри стик грунта и трубы. При этом место изменения внутреннего давления не должно быть в тройниковом сечении. Далее, определяются граничные условия рассчитываемой системы, т. е. жесткости упругих связей. Связи, препятствующие углу поворота, поперечному и продольному перемещениям но отношению к прямолинейному элементу трубопровода, могут находиться в любой узловой точке. Если связь в какой-либо узловой точке в каком-либо направлении отсутствует, то се жесткость равна нулю. Если связь полностью ограничивает перемещения (неподвижная опора), то ее жесткость принимается равной бесконечности и вводится в форму исходной информации число 0,1 • 1021. Если к углу поворота примыкает длнннын прямолинейный участок, то на определенном расстоянии от него трубопровод можно считать защемленным, т. е. принять жесткости всех трех связей равными бесконечности. Если рассчитываемая конструкция примыкает к открытому надземному переходу с компенсатором, то, пренебрегая отпором компенсатора, жесткости в месте выхода подземного трубопровода на поверхность можно принять равными нулю.
Нумерацию узлов можно проводить в любой последовательности, причем узлами являются и крайние точки рассчитываемой системы даже при отсутствии в них связей. Рекомендуется нумеровать узлы таким образом, чтобы разность между номерами двух соседних узлов была наименьшей.
Положительные направления внешних усилий и ориентация упругих связей приведена на рис 44 При необходимости действующие усилия следует разложить на составляющие по принятым здесь направлениям с учетом их знака.
Входная информация заносится в специально разработанные формы, содержащие два листа. Первая строка первого листа формы содержит ин формацию общего плана: наименование отдела (8 символов), заказа (8 символов), варианта (8 символов) и объекта (56 символов). Во вторую строку первого листа заносятся значения параметров, постоянных иа всей рассчитываемой конструкции k число узловых точек; п,, — коэффициент перегрузки для внутреннего давления, определяемый согласно нормам; а — коэффициент линейного расширения материала труб; ? — модуль упругости материала труб ц—коэффициент Пуассона материала трубы; утр объемный вес материала труб; игр — коэффициент перегрузки для грунта опре леляемый согласно нормам; h расстояния от верха трубы до поверхности грунта.
Начиная с третьей строки второго листа формы, построчно для каждой узловой точки (где стыкуются два или три элемента), обходя их по возрастающим ,номерам, заносятся псе характеристики в следующей последовательности: i — номер узловой точки; /', k, т — номера соседних узловых точек; если к узлу примыкает одии элемент, то ft и т принимаются равными пулю, если два элемента, то т=0; fp.j, ф,*, <pjm — углы, составляемые соответственно элементам ij, ik и im с вектором (ф — угол, образованный вращением элемента относительно узловой точки по часовой стрелке до совмещения с принятым направлением вектора, направление вектора можно принять любым, но одинаковым для всех узлових точек; желательно для
ускорения счета его направление принять совпадающим с осью больши ства элементов); qu— жесткость упругой связи, препятствующей углу поворота узловой точки; tja — жесткость упругой связи, препятствующей По| перечному перемещению узловой точки; q3i—жесткость упругой связи, препятствующей продольному перемещению узловой точки; /?ц—внешни изгибающий момент, приложенный к узловой точке; R2.—внешняя поперечная сила; R3i — внешняя продольная сила.
Число горизонтальных строк, начиная с третьей, должно быть равно числу узловых точек, т. е. параметру к, внесенному во вторую строку пер' вого листа формы. Затем необходимо заполнить второй лист формы. j
Начиная с первой строки второго листа формы, для каждого элемента в порядке возрастания номеров заносится вся информация в следующей последовательности: н — номер начала элемента; ж — номер конца эл мента; I — длина элемента; fi—толщина стенки трубы; At — положительный температурный перепад; р — нормативное (рабочее) давление; цгр коэффициент Пуассона грунта; Е,р — модуль деформации грунта; «ргр угол внутреннего трения грунта; — объемный вес грунта; сгр — сцепл ние грунта; сх „ — коэффициент касательного сопротивления грунта; т|Гр —| коэффициент, определяемый в зависимости от отношения расстояния см трубы до стенки траншей к расстоянию от верха засыпки до оси трубы gi — сопротивление грунта поперечным перемещениям трубы, соответству, щее пересечению первых двух ветвей диаграммы «сопротивление грунта — перемещение»; g2 — сопротивление грунта поперечным перемещениям трубы, соответствующее пересечению второй и третьей ветви диаграммы «соп[ тивление грунта—перемещение»; Ci—тангенс угла наклона к оси абецн' второй ветвн диаграммы «сопротивление грунта—перемещение»; с? — тан-, гене угла наклона к оси абсцисс третьей ветви диаграммы «сопротивление грунта — перемещение».
Подготовка исходных данных для расчета выполняется на перфокартах на Устройстве ЕС-1090. Каждая строка бланка перфорируется на отдельно перфокарте. Первая строка бланка содержит текстовую информацию, все последующие — цифровую.
Для контроля заданных исходных данных и правильности их перфо рации распечатывается вся исходная информация рассчитываемой слстемыЛ Прн этом печатаются необходимые комментарии.
Следующая таблица содержит результаты расчета. Первая графа, названная «шифр» участка, содержит цифры, обозначающие начало и конец участка в том виде, в котором они приняты при формировании печати. Вторая графа, названная «текущие координаты», показывает для каких сечений участка даны последующие результаты. Цифра 0 соответствует началу участка, 0,5 — середине, 1—концу. Третья графа содержит значение изгибающего момента. Знак плюс означает, что растянуты правые волокна, если смотреть от начала участка к концу Четвертая графа содержит значение продольного осевого усилия в стенках трубы Знак плюс означает, что продольное осевое усилие — растягивающее. Пятая графа содержит значение поперечной силы. Знак плюс указывает, что на левом конце элемента поперечная сила сдвигает этот конец влево относительно оси, если смотреть от начала участка к концу, а на правом конце — в протнвопо-'' ложную сторону. Шестая графа содержит значение поперечных, относительно данного участка, перемещений. Знак плюс показывает, что перемещение направлено влево относительно участка, если смотреть от его начала к концу. Седьмая графа содержит значение продольных, относительно данного участка, перемещений. Знак плюс означает, что перемещение направлено от начала элемента к его концу. Восьмая графа содержит значения, угла поворота сечения Знак плюс означает, что поворот осуществляется по часовой стрелке, если смотреть от нача,па элемента к его концу.
В качестве иллюстрации применения программы «Узлы-78», рассмотрена схема трубопровода, изображенная на рнс 45. Она представляет собой систему, расположенную в горизонтальной плоскости при глубине за-ложепня трубопровода (до верхней образующей трубы) 100 см. Ь первом и втором узлах имеется заделка, ограничивающая продольные, поперечные и угловые перемещения. Четырнадцатый н пятнадцатый узлы представляют собой место выхода на поверхность трубы, которая заканчивается заглушками, ограничений по всем компонентам перемещений нет. Две магистрали выполнены из труб размером 1420Х19 мм, перемычка — из труб 320X14 мм. Внутреннее давление и температурный перепад одинаковы для всего участка и равны р=5,4 МПа, Д/'=43 °С. Физико-механические характеристики грунтов: модуль деформации грунта ?гр=28 МПа. угол
| -50п ---ОТм W0n | ||
| Я® " / фМго/гэ с* tv 0 фйго/ГЗ П 'нитка | 1 ЗГ to i}4 © Г 1 | ш ^¦фюго/w фМо/19 ® ® \ © |
|
- х ¦ --Шм-^ |
¦*r—JU0w—** | |
Рис. 45. Схема рассчитываемой системы трубопроводов
внутреннего трения фгр=32°, объемный вес грунта Yrp=16 к11/м3, сцепление Сгр—0,002 МПа. Геометрические параметры рассчитываемой системы и нумерация узлов приведены на рис. 45.
Информация, выдаваемая после расчета на ЭВМ, состоит из двух частей: исходные данные и результаты расчета системы. Обратим внимание, что под шифром участка, например I—6, понимается, что начало участка находится в узле 1, конец — в узле 6, под текущей координатой 1, 0,5; 0 понимается соответственно конец, середина и начало участка.
В результате расчета находятся три компонента усилий — изгибающий момент, продольное усилие в стенках трубы и поперечная сила, а также трн компонента перемещений. По компонентам усилий определяются напряжения в трубопроводе и соединительных деталях, по компонентам перемещений — перемещения элементов конструкции
Прочностной расчет в программе не реализован, так как в нормативных документах по проектированию магистральных трубопроводов не даны предельные состояния для соединительных деталей при действии трех компонентов усилий и внутреннего давления продукта.
Для оценки предельных состояний соединительных деталей [15] дополнительно, учитываются коэффициенты интенсификации напряжений, которые зависят от принятой конструкции деталей и характера нагружения
Отдел:
Объект;
Расчет прочности разветвленных подземных трубопроводов («Узлы-78»)
Исходные данные:
Количество узлов
Коэффициент линейного расширения
Коэффициент Пуассона металла
^«•-1.........- - - -
15
•000012
0.3
0.83
Коэффициент перегрузки давления Модуль упругости металла, МПа Объемный вес металла, кН/м3
Высота засыпки, см
210 000
78.5
100
Коэффициент перегрузки грунта
Примыкающие узлы
Узел (
4>ik
Vim
*/
*1
m
1
2
3
4
5
6
7
8 9
10
11
12
13
14
15
О
О
2
3 II
5
5
4
3
6
4 8 9
13
10
6
3
9
8
7
10
12
О
13 15 0 7
14 О 0
О
о
4 11
6
J
О
12
О
О
5 О О о о
0.0
0.0
270.0
180.0 180,0
150.0
270.0 270 0 270 0 270 0 180 0 1SOO
270.0 270 0
270.0
90.0
90.0 900
90.0
90.0
90.0 180.0
0.0
90.0
90.0 0.0 0.0
90.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 270.0 0.0 0 0 00 о о 0.0 0.0 0.0 0.0 0.0
О 1Е20 0 1Е20 00 0.0 0.0 0.0 0.0 0.0 0.0 0.0 о о 0.0 0.0 0.0 0.0
0.1Е20 0.1Е20 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0 0 0.0
О IE20 О 1Е20 0.0 0.0 0.0 0.0 0.0 0.0 0.0 00 0.0 0.0 о о 0.0 0.0
| 00 |
0.0 | 0 0 |
|
0.0 | 0.0 | 0.0 |
| 0.0 | 0 0 |
0.0 |
| 0.0 | 0.0 | 0.0 |
| 0.0 | 0.0 | 0.0 |
| 0.0 | 0.0 | 0.0 |
| 0 0 | 0.0 |
0.0 |
| 0.0 |
0.0 | 0 0 |
| 00 | 0 0 | 0 0 |
| 00 | 0.0 | О.о |
| 0.0 | 0.0 |
00 |
| 0.0 |
0.0 | 0 0 |
| 0.0 | 0.0 | 0 0 |
| 00 | 0.0 | 0.0 |
| 0.0 | 00 |
00 |
| Шнфр участка | !, см | 0„, см |
в, см | Л*, °с |
р, МПа | ^гр |
Егр. МПа | Фгр, градусы | Vrp. кН/м’ |
| 1—ь | 13 000. |
142.0 | 1 90 | 43.0 | 5,4 | 0.30 |
28 | 32.00 | 16 |
| 2—3 | 5 000. |
142.0 | г.90 | 43.0 | 5,4 | 0.30 |
28 | 32.00 | 16 |
| 3—9 | 10 ООО. |
142.0 | 1.90 | 43.0 | 5,4 | о.зо |
28 | 32.00 | 16 |
| 3—4 | 1 220. |
102.0 | 1.60 | 43.0 |
5,4 | 0 30 | 28 | 32.00 | 16 |
| 4—8 | 200. | 32.0 | 1 40 | 43.0 |
5,4 | 0.30 | 28 | 32.00 | 16 |
| 4—11 | 380. | 102.0 | 1.60 | 43.0 |
5,4 | 0.30 | 28 |
32.00 | 16 |
|
5—11 | 380. | 102.0 |
1 60 | 43.0 | 5,4 | о.зо | 28 |
32.00 | 16 |
|
5—7 | 200 | 32.0 |
1 40 | 43.0 | 5,4 | 0.30 | 28 |
32.00 | 16 |
|
5—6 | 1 220. | 102 0 | 1 60 | 43.0 |
5,4 | 0.30 | 28 |
32.00 | 16 |
|
6—10 | 10 ООО | 142 0 | I 90 | 43.0 |
5,4 | о.зо | 28 | 32.00 | 16 |
| 7—12 | 380 | 32.0 | 1 40 | 43.0 |
5,4 | 0.30 | 28 |
32.00 | 16 |
|
8—12 | 380. | 32.0 |
1 40 | 43.0 | 5,4 | 0.30 | 28 |
32.00 | 16 |
|
9—13 | 10 000. | 142 0 | 1 90 | 43.0 |
5,4 | 0.30 | 28 | 32.00 | 16 |
| 10—15 | 10 ООО. | 142 0 | 1 90 | 43.0 |
5,4 | 0.30 | 28 |
32.00 | 16 |
|
3—14 | 10 ООО | 142 0 | 1 90 | 43.0 |
5,4 | 0.30 | 28 |
32.00 | 16 |
|
Шифр участка | срр, Н/см* | сХ0, Н/см» |
Уу МПа | ?2. МПа |
сг, МПа/см |
сд. МП а/см | СН | ¦Чгр |
| 1—6 | 0,20 | 2,60 |
999. | 999. | 0.10Е—30 | О.ЮЕ-ЗО | 0.38 |
0.72 |
| 2—3 |
0,20 | 2,60 | 999. |
999. | 0.10Е—30 | 0 10Е-30 | 0.38 | 0.72 |
| 3—9 | 0,20 |
2,60 | 999 | 999. |
0 10 Е—30 | 0 10Е-30 |
0.38 | 0.72 |
|
3—4 | 0,20 | 2,60 |
999 | 999. | 0 10Е—30 | О.ЮЕ-ЗО | 0.38 | 0 72 |
| 4—8 |
0,20 | 2,60 | 999 | 999. | 0 10Е—30 |
О.ЮЕ—30 | 0.38 | 0 72 |
| 4—11 | 0:0 |
2,60 | 999. | 999. | 0.10Е—30 | 0.10Е—30 |
0 50 | 0.72 |
|
5—11 | 0,20 | 2,60 |
999 | 999. | 0 10Е—30 | 0 10Е-30 | 0.50 | 0 72 |
| 5—7 |
0,20 | 2,60 | 999 | 999. | 0 10Е—30 |
О.ЮЕ-ЗО | 0 90 | 0.72 |
| 5—6 | 0,20 |
2,60 | 999 |
999. | 0.10Е—30 | 0 10Е-30 | 0 50 | 0.72 |
| 6—10 | 0,20 |
2,60 | 999. | 999. |
0 10Е—30 | О.ЮЕ-ЗО |
0.38 | 0.72 |
|
7—12 | 0.20 | 2,60 |
999. | 999. |
0.10Е—30 | О.ЮЕ-ЗО |
0.90 | 0.72 |
|
8—12 | 0,20 | 2,60 |
999. | 999. |
0.10Е—30 | О.ЮЕ—30 |
0,90 | 0.7 2 |
|
9—13 | 0,20 | 2,60 |
999. | 999. |
ОЛОЕ-ЗО | О.ЮЕ-ЗО |
0.38 | 0.72 |
|
10—15 | 0,20 | 2,60 |
999. | 999. | 0 10Е—30 | О.ЮЕ-ЗО | 0.38 | 0.72 |
| 3-14 |
0,20 | 2,60 |
999. | 999. |
О.ЮЕ-ЗО | О.ЮЕ-ЗО |
0.38 | 0.72 |
| Шифр участка | Координаты |
Изгибающий момент, Н м |
Продольное усилие, Н |
Поперечная сила, Н |
Поперечное перемещение, см |
Продольное перемещение, см | |||
| i-б | 1.0 | 0.108Е | 07 | —.349Е |
07 | 0.238Е | 06 |
0.961 Е 00 | 0.332Е—01 |
| 1—6 | 0.5 | — 357Е | 03 | —.361Е |
07 | 0.367Е | 02 | 0.862Е—03 | 0.603Е—02 |
| i-б | 0.0 |
—.116Е | 01 | —.363Е | 07 | —. 112Е—00 | — .112Е—20 | —126Е.—12 | |
| 2—3 | 1.0 |
—-111Е | 07 |
—.362Е | 07 | —.245Е | 06 | —.995Е 00 |
0.232Е—02 |
| 2—3 |
0.5 | 0.109Е | 06 |
—.363Е | 07 |
0.153Е | 05 | 0.483Е—01 | 0.959Е—03 |
| 2—3 | 0.0 | —.714Е |
04 | —.363Е | 07 |
—.987Е | 03 |
—.987Е—17 | —. 126Е—12 |
| 3—9 | 1 0 |
—.242Е | 02 | — 348Е | 07 | 0.267Е |
01 | —.390Е 00 |
0.338Е—01 |
| 3—9 |
0.5 | 0.360Е | 08 |
—.359Е | 07 |
0.908Е | 03 | — .350 Е 02 | 0.928Е—02 |
| 3—9 | 0.0 | —.110Е |
07 | —.362Е | 07 |
0.244Е | 06 | —.995Е 00 | 0.232Е—02 |
|
3—4 | 1.0 | 0.860Е |
04 | 0.372Е | 07 | 0.340Е | 04 |
0.246Е—01 | —.237Е 00 |
| 3—4 | 0.5 |
—.390Е | 04 | 0.387Е | 07 | 0.845Е |
03 | 0.772Е—02 | —-610Е 00 |
| 3—4 | 0.0 | —.680Е | 04 |
0.413Е | 07 | 0.610Е | 03 | —.232Е 02 |
—.995Е 00 |
| 4—8 |
1.0 | —.328Е | 04 |
0.413Е | 06 |
—.400Е | 04 | 225Е 00 ¦ | 0.899Е—01 |
| 4—8 | 0.5 | — 442Е |
05 | 0.411Е | 06 |
—.558Е | 03 | —.233Е 00 | 0.326Е—01 |
|
4—8 | 0.0 | —.219Е | 04 | 0.411Е |
06 | 0.298Е | 04 |
—.237Е 00 | —.246Е—01 |
| 4—II | 1.0 |
0.727Е | 04 | 0.360Е | 07 | 0.370Е |
03 | 0.274Е—01 |
—.112Е—01 |
| 4—11 |
0.5 | 0.125Е | 04 |
0.361Е | 07 | — .959Е | 03 | 0.271Е—01 | —.124Е 00 |
| 4—11 | 0.0 | 0.10SE |
05 | 0.364Е | 07 |
—.222Е | 04 |
0.246Е—01 | —.237Е 00 |
| 5—11 | 1.0 |
—.728Е | 04 | 0.360Е | 07 | 0.229Е |
03 | —.274Е—01 |
0.112Е—01 |
| 5—11 |
0.5 | —.108Е | 04 |
0.361Е | 07 | 0 152Е | 04 | —.258Е—01 | —.101Е 00 |
| 5—11 | 0.0 | - 129Е |
05 | 0.363Е | 07 |
0.268Е | 04 | — .216Е—01 | —.214Е 00 |
|
5—7 | 1.0 | 0.442Е | 04 | 0.412Е |
06 | 0.567Е | 04 |
0.208Е 00 | 0.929Е—01 |
| 5—7 | 0.5 |
0.472Е | 03 | 0.411Е | 06 | 0.250Е |
04 | 0.212Е 00 |
0.356Е—01 |
| 5—7 |
0.0 | —.571Е | 03 |
0.410Е | 06 |
—.706Е | 03 | 0.214Е 00 | —.216Е—01 |
| 5—6 | 1.0 | —.222Е |
05 | 0.403Е | 07 |
- 557Е | 04 |
—.332Е—01 | 0.961Е 00 |
| 5—6 | 0.5 | 0.812Е | 03 | 0.377Е |
07 | —.205Е | 04 |
—.776Е -02 | 0.582Е 00 |
| 5—6 | 0.0 | 0 135Е | 05 | 0.363Е |
07 | —.ЗЗЗЕ | 04 | 0.216Е—01 | 0.214Е 00 |
| 6—10 | 1.0 |
0 233Е | 02 | -.164Е | 07 | —.238Е |
01 | 0.304Е 00 | 0.442Е 00 |
| 6—10 | 0 5 |
— .364 Е | 08 | — .398Е | 07 | —.838Е |
03 | 0.297Е—-02 |
0.122Е 00 |
| 6—10 |
0.0 | 0.106Е | 07 |
—.348Е | 07 |
—.235Е | 06 | 0.961Е 00 | 0.332Е—01 |
| 7—12 | 1.0 | —319Е |
04 | 0 403Е | 06 |
—.314Е | 03 |
0.478Е—01 | 0.810Е-02 |

Шифр
участка
Координаты
Изгибающий момент. И м
|
7—12 | 0.5 | — .181Е 04 |
| 7—12 | 0.0 |
0.440Е 04 |
| 8—12 |
1.0 | 0.321Е 04 |
|
8—12 | 0 5 | 0.213Е 04 |
| 8—12 | 0.0 |
—.325Е 04 |
| 9—13 |
1.0 | — 196Е—03 |
| 9—13 | 0.5 | 0.830Е 03 |
| 9—13 | 0.0 | — .242Е 02 |
|
•J0—15 | 1.0 |
—.119Е—03 |
| 15 |
0.5 | —.963Е 03 |
|
я к 1 ”-15 | 0.0 |
0.234Е 02 |
| Ф4 |
1.0 | 0.212Е—08 |
| ^ ? 5’ гс ? ? ю Е 2 о о К ? “ 9 | 0.5 0.0 |
0.891 Е-02 —.216Е—03 |
11 р о д О л ж с и и о.
|
долыюс усилие, Н | Поперечная сила> Н | Поперечное перемещение» см | Продолвное перемет ние, см |
| 0.403Е 06 | —.186Е 04 | 0.655Е—01 | — .100Е 00 |
| 0.411Е 06 | — ,416Е 04 |
0.929Е—01 | — .208Е 00 |
| 0.401Е 06 | 0.943Е 02 |
—.4786—01 | —.810Е—02 |
| 0.404Е 06 | 0.158Е 04 |
—.613Е—01 | —.116Е 00 |
| 0.412Е 06 | 0.375Е 04 |
— .899Е—01 | —.225Е 00 |
| — .164Е 07 | —.775Е—05 |
0.856Е—07 | 0.442Е—00 |
| —.308Е 07 | 0.465Е—02 |
0.437Е—07 | 0.122Е 00 |
| —.348Е 07 | 0.2676 04 |
0.131Е 05 | 0.338Е—01 |
| 0.454 Е 07 | —331Е—05 |
—.377Е—05 | 0.284Е 01 |
| 0.150Е 06 | —342Е—02 |
—.503Е—07 | 0.122Е 01 |
| —.160Е 07 | —.257Е 01 |
— .117Е— 05 | 0.442Е 00 |
| 0.450 Е 07 | 0.378Е- 09 |
0.250Е—09 | 0.284Е—01 |
| 0.150Е 06 | — .134Е-06 |
0.202Е—11 | 0.122Е 01 |
| —.160Е 07 | —.826Е—05 |
0.279Е—09 | 0.442Е 00 |
м
я „ о, п
° н я
о я
О Т5
о о .
? 1 » х о
S 1а ш s
я с'
(О "* •
РАСЧЕТ ПОДЗЕМНЫХ ТРУБОПРОВОДОВ, ПРОКЛАДЫВАЕМЫХ НА ОБВОДНЕННЫХ УЧАСТКАХ ТРАССЫ
11а подземные трубопроводы, прокладываемые на обводненных участках трассы, дополнительно действует нагрузка от выталкивающей силы воды, н сопротивление обводненного грунта поперечным и продольным перемещениям трубы уменьшается. В связи с этим даже трубопроводы, прокладываемые в минеральных грунтах, необходимо дополнительно закреплять против потери устойчивости. Опыт эксплуатации показал, что расчет таких трубопроводов с учетом действительных условий их работы приобретает важнейшее значение.
Учитывая возможно большие перемещения трубопровода прн малом сопротивлении грунта его перемещениям, для всех участков таких трубопроводов обязательна проверка деформаций трубы при действии всех нагрузок и воздействий. Это особенно относится к участкам трубопровода, имеющим начальный изгиб в вертикальной плоскости нли относительно большие углы поворота в горизонтальной плоскости.
Для оценки напряженно деформированного состояния подземных трубопроводов, прокладываемых на обводненных участках, разработан комплекс программ, алгоритмы которых позволяют учесть характер взаимодействия трубопровода с грунтом, балластировку трубопровода и особенности, связанные с геометрической и физической нелинейностью.
§ 1. Определение нагрузки от выталкивающей силы воды
Поперечная нагрузка иа трубопровод от выталкивающей силы воды зависит от уровня воды относительно трубы. Если пренебречь кривизной трубопровода, то выталкивающая сила, действующая на единицу длины трубопровода, определяется по формуле
к
8
(а — sin а),
(9 1>
Qb — Yb-F обв- F обв —
где у* — удельный вес воды с учетом растворенных и взвешенных в ней веществ; Dn — наружный диаметр трубы с учетом изоляционного покрытия и футеровки; а — угол, характеризующий уровень воды относительно оси трубы.
2л — accos 2 (ft
(9.2)
2 arccos
2jt, есл и
2 (ftp ¦— h к)
Он
D„
О, если
fto)
ftjj ^5 ft*
• если ft < ftB ftc;
если ft„ < ftB < Я; ftfi H,
J. J, от верха засыпки до уровня воды; ft, ho, Н соответ-черха засыпки до верхней образующей, оси и ниж-•с»
¦&С
к и
Рис. 46. Принятые обозначения подземного трубопровода при обводнении
nDi
0,8 А
hVb
<7 в
§ 2. Сопротивление грунта перемещениям трубы
При расчетах подземных трубопроводов, прокладываемых на обводненных участках, как показали проведенные во ВНИИСТе эксперименты, можно пользоваться теми же моделями грунта, что н для трубопроводов в обычных условиях. При этом изменяются только количественные параметры модели. На основании проведенных экспериментов установлены эмпирические формулы для определения предельной удержи-лающей способности грунта. В зависимости от уровня воды предельное сопротивление грунта поперечным вертикальным вверх перемещениям трубы определяется по формулам прн
<?пр. гр = D,i J Yrp+ Yb3E ^ — hn —— j -4 k |l Yrp^n (2Л0 -f- hK) -f- Ybsb (Ло AB)2j tg 0,7<Prp ^ ¦
--—— ^обв) + Ybsb [ (ho — hB)DK
0,7 h,^
-j; (»4)
FОби J 4' Yb3b J (hc — — —^o6b^J “t-
+ k [vrp^B (2ft0 — hB) tg 0,7 фгр + Увзв — hB)2 tg 0,7 <prp + 1 ¦
L cos 0,7qVpJ
(9.5)
(9.6)
sOJqVpJ’
cos 0,7фгр nDl
<7пр. гр - Yrp
¦) +*fvrp^tgO,7<fVp+ -°’-^
IYpDh(ao-
p.rp
8
cos I
где DB — наружный диаметр трубы; Yrr — объемный вес грунта в естественном (необводненном) состоянии; объемный вес грунта во взвешен
ном состоянии; k — коэффициент, характеризующий прнзму выпора, принимаемый равным единице для трубопроводов условным диаметром от 100 см и более и меньше единицы—для трубопроводов меньших диаметров (к Дн/100); фгр—угол внутреннего трения грунта; сгр -сцепление грунта: Fvok — площадь сечення трубы, находящейся в обводненном состоянии Объемный вес грунта во взвешенном состоянии
(9.7)
где Yy—удельный вес грунта (скелета); у»—удельный вес воды, е — ко эффициент пористости
Прн назначении уровня обводнения рассчитываемого участка трубопровода следует исходить не только нз данных непосредственных изысканий трассы трубопровода, но и учитывать прогнозируемый уровень поды, связанный с гидрогеологическими условиями и их изменениями во времени При назначении объемного веса необводненного грунта необходимо учитывать изменение его влажности за счет капплляриого подсоса из ннжней
обводненной части грунта. Коэффициент пористости грунта должен отражать не только результаты изысканий, но н способ и время обратной засыпки траншеи грунтом.
При проектировании трубопроводов на участках, сложенных, грунтам» которые могут перейти в жидкопластичсское состояние, прн определении выталкивающей силы следует вместо объемного веса воды принимать объемный вес разжиженного грунта, определяемый по данным инженерны;, изысканий. Сопротивление грунта продольным перемещениям трубы зависит от уровня воды и относительной глубины заложения трубопровода. Предельное сопротивление грунта продольным перемещениям трубы на единицу ее длины можно определить по следующей формуле:
'пр.гр = 2лФн
(vrp + YB3B\ tgqYp + 0,6nD^ .
(9 8>
При расчетах по формуле (9.8) следует учитывать, что если hb^h^ то необходимо принимать hB=h0. Коэффициент Сл, учитывающий образование свода естественного равновесия при продольных перемещениях трубы, определяется по следующим зависимостям, аппроксимирующим эксперимен-
тальные кривые: для песчаных грунтов
с/,— 0,416—---0,056 — +0,095;
(9.9)
для глинистых грунтов
сь^ 0,367 —--0,046 -f 0,06.
§ 3 Сопротивление перемещениям трубы при наличии балластировки трубопровода
Прн определении сопротивления поперечным перемещениям трубы необходимо учитывать не только сопротивление грунта, но и сопротивление, оказываемое дополнительными закрепляющими устройствами. Расчетное предельное сопротивление поперечным перемещениям трубы вверх можно записать в виде
^пр “ гг. т т Пгр*?пр. гр» (®'
где qa. г — положительная плавучесть трубопровода; пгР коэффициент перегрузки для грунта, принимаемый согласно СНиП 11-45—75 равным 0,8; 9пр. гр — предельное сопротивление грунта.
Расчетная положительная плавучесть трубопровода определяется по формуле
<?п. т *?тр ”1 ^доп ^Выт* (9-12)^
где Qrp — расчетный вес единицы длины трубопровода; <?„ыт—расчетная выталкивающая сила на единицу длины трубопровода.
Под <7доп следует понимать величину прнгрузки на единицу длины трубопровода. При расчете на эксплуатационный период в оп включается, расчетный вес продукта Если балластировка осуществляется с помощью | грузов, то при вычислении <7доп следует учитывать выталкивающую силу •
воды, действующую на данную конструкцию. При вычислении расчетной
положительной плавучести по формуле (9.12) необходимо нормативные значения всех составляющих умножать на коэффициент перегрузки, который в соответствии с нормами следует принимать: для собственного веса трубопровода равным единице; выталкивающей силы воды —1,05—1,15; для веса железобетонных грузов—0,95; для сплошного обетонировапия — 0,93— 0,9; для веса продукта — 0,95. Если трубопровод закрепляется анкерами, -со величина <jRon вычисляется по формуле
•7доп = Байк 1< (9-13)
г
где Банк — расчетное усилие (допускаемая нагрузка) на анкерное устройство; I — расстояние между анкерами.
Для винтовых анкеров согласно СНиП II-45—75 расчетное усилие (Банк) определяется по формуле
Бяяк = 2&гр^анкЛ1анк> (9.14)
где г — число анкеров в одном анкернам устройстве; kTp — коэффициент несущей способности грунта, в котором находятся лопасти анкеров.
гК™’ ГР>™ ‘гр
Л’ан„—максимальная (критическая) нагрузка на один винтовой анкер, завинченный в грунт I группы на глубину не менее шести диаметров лопасти.
|
Диаметр | Л/„ „ н |
Диаметр | N Н |
| анкера, мм | анк» А1 | анкера, мм | анк» л 1 |
| 100 | 6 500 | 300 | 30 000 |
| 150 | 7 500 |
400 | 53 000 |
|
200 | 13 500 | 500 |
83000 |
| 250 |
21 000 | 600 | 120000 |
>Плнк — коэффициент условий работы анкерного устройства, принимаемый равным 0,5 при z=g;2 и 0,4 —при г>2.
В последнее время стали использоваться свайные анкера раскрывающегося типа АР 401, обладающие повышенной несущей способностью Методика по определению максимальной критической нагрузки для таких анкеров, учитывающая как глубину заложения свайных анкеров, так и физико-механические характеристики грунта, изложена в [26]. Предельное сопротивление такого анкера определяется по формулам;
При Ланк/^авк^5
N анк Yrp^ Ь SCrpl (9.15)
Прн ЛапкМ, HJK >5
N анк
(ЛсГ р Вугр^аяк) F анк» (9.16)
где Лащ, — глубина заложения лопасти от дна траншеи; daHK — днаметр лопасти анкера уГр — средневзвешенный объемный всс грунтов, залегающих от дна траншеи до отметки заложения анкера, определяется с учетом уровня обводнения; V — объем конуса выпирания.
<^анк ~Г hанк tg фгр . cos <ргр
фгр- угол внутреннего трення; сГр — сцепление грунта; Faвк — суммар-
nha
| • угла |
внутреннего | трения фгр: | |||
| фгр | А | В |
Фгр | А |
В |
| 10 |
6,2 | 2,1 | 26 |
16,8 | 9,2 |
|
14 | 7,1 | 2,8 |
28 | 21,2 | 12,3 |
| 18 | 8,6 |
3,8 | 30 | 26,9 |
16,5 |
| 22 |
11,1 | 5,5 | 32 |
34,4 | 22,5 |
При определении предельного сопротивления продольным перемещени также необходимо учитывать положительную плавучесть трубы. Однако при этом необходимо учитывать, что анкера практически не препятствуют продольным перемещениям трубы, т. е. предельное сопротивление должно вычисляться по формуле '
(9.19)
¦пр
гр
к) ^ *Ргр Н" ^пр. гр]
В этой формуле предельное сопротивление грунта продольным переме-1 щениям трубы определяется по (9.8).
§ 4 Определение пригрузки для упругого изгиба трубопровода
Равномерную нагрузку, необходимую для изгиба трубопровода по заданному радиусу обычно определяют нз условия, при котором прогиб балки посередине пролета, равного расстоянию между началом и концом дуги кривой (хорде), равнялся стрелке кривой. Тогда пригрузка определяется по формуле
fEI
Бкзг = - ( 9.20)
Стрелка прогиба f и длина хорды кривой L (пролет) определяются, исходя нз принятой формы кривой в виде окружности:
1 = р — 0,5 V4P2 L2’
(9.21) (9 22)
L — 2р sin р'2,
где р — радиус окружности; р — угол поворота.
Коэффициент k отражает граничные условия. Например, для вогнутых кривых значение k принимается равным 5/384, т. е. концы балки счита-' ютея шарнирными. Если считать, что одни конец балки защемлен, а другой шарнирный, то к= 1/185
Н А. Кухтериным и автором предложен иной подход к определению прнгрузки для изгиба трубопровода. Будем исходить нз условия, что нам необходимо обеспечить заданный угол поворота трубопровода при ограничениях по изгибным напряжениям трубы. Пренебрегая, из-за малости углов поворота, несимметричностью системы, для рассматриваемой балки можно принять, что углы поворота оси балки по концам равны но абсолютной величине половине угла поворота трассы. На рис. 47, а изображена принятая расчетная схема для вогнутой кривой, причем, как и ранее для дуги окружности, расстояние от места поворота трубопровода до условной вершины названо тангенсом Т, а от оси трубы до условной вершины — биссектри-
Рис. 47. Расчетная схема поворота трубопровода с помощью упругого
изгиба
сой Б Из решения уравнения поперечного изгиба балки при принятых граничных условиях:
E!dAy'dx = Базт; (9.23)
у = dzy/dx2 = 0; dyjdx ± р/2 прн х=0, L, (9 24)
находится форма упругой линии трубы
Вх /j'и^г 1 - .j I Б\щгХ^
У~—---—— *3Н--5151—, (9.25)
2 12 EJ 24 EI '
где EI—нзгнбная жесткость трубы; БМзг — интенсивность поперечной нагрузки; р—угол поворота, L—длина волпы изгиба.
Отметим, что решение дифференциального уравнения (9.23) содержит четыре произвольных постоянных, в то время как граничных условий у нас шесть. Дополнительное граничное условие служит для определения длины волны изгиба, которая определяется по формуле
, Г 12?7р
Так как обычно в практике проектирования прниято характеризовать упругий изгнб минимальным радиусом оси трубопровода то на основании (9.25) и (9.26) находим минимальный раднус
з
2 , / 12 Е1
р-Т
\/ -• (9-27)
Отсюда искомая поперечная распределенная нагрузка
Таким образом, на основании формулы (9.28) при заданном угле поворота оси траншеи и минимальном радиусе упругого изгиба трубопровода, определяющих максимальное напряжение в стенках трубы при изгибе, вычисляется необходимая равномерно распределенная нагрузка. С использованием формулы (9 28) можно также определить тот минимальный угол поворота, который можно осуществить за счет изгиба трубопровода под собственным весом при укладке его в пеобводненную траншею прн задан-
ном радиусе, илн минимальный радиус при заданном угле поворота В этом случае величина Бизг принимается равной весу единицы длин трубы:
2El
<?трР3
4?/
99трР-
Pmin — —
(9 29) (9.30)
Pmin — 2
Запишем также формулы для определения необходимых геометрически параметров. Длина волны изгиба определяется по (9.26); ее также можно! используя (9.28), выразить через угол поворота и минимальный радиус оси изгиба
(9.31)
2
Расстояние от начала кривой до вершины поворота (см рис. 47, а)
3 рр
(9.32)
cos р,.'2
Расстояние от низа кривой до вершины поворота (см, рис. 47, а)
Б ^4т-Рр(-3.2^Р 2-Р)% 0,141р2р.
(9.33)
04
В некоторых случаях необходимо вычислить промежуточные отметки дна траншеи. В связи с этим запишем уравнения изогнутой оси трубопровода в системе координат, приведенной на рис. 47, а:
(9.34)
3
?изг
(9.35)
El
9р2?„зг
(9.36)
где I — длина волны изгиба, определяемая по (9.31); %=xfL — безразмерная абсцисса точки.
Получим решение для параметров упругого изгиба трубопровода по выпуклой кривой с темн же предпосылками расчета, как и ранее. Все обозначения принимаем аналогичными предыдущим (рис. 49,6). Приведем без вывода необходимые расчетные формулы: длина волны изгиба
L - 2 {/
минимальный радиус упругого изгиба
3
пригрузка для упругого изгиба трубопровода е углом поворота 0 и минимальным радиусом оси изгиба р
минимальный угол попорота прн изгибе трубопровода под действием собственного веса трубы
минимальный радиус оси изгиба трубы под действием собственного веса лри заданном угле поворота
Pmin-2]/ ’ (9'39)
длина вотны изгиба, выраженная через угол поворота и минимальный радиус оси изгиба:
L = Зрр; (9.40)
расстояние от начала кривой до вершины поворота
2 соь р/2
расстояние от вершины кривой до вершины угла поворота
Б - Рр (-|- tg| 2 - р) « 0,188р2р; (9.42)
уравнение упругой линии в системе координат, приведенной на рис. 47, б:
(9.43)
где Р — угол поворота; 1=Ц2 — половина длины волны изгиба; %—xll — безразмерная абсцисса точки.
§ 5. Устойчивость положения и продольная устойчивость подземного трубопровода
Расчет трубопровода, как и любой другой строительной конструкции, должен производиться на нагрузки и воздействие в условиях строительства и эксплуатации. В процессе строительства должно обеспечиваться проектное положение подземного трубопровода. Не касаясь технологии нропзподства работ по укладке трубопровода на дно траншеи, рассмотрим те нагрузки и воздействия, которые действуют при этом, а также условия обеспечения проектного положения трубопровода.
Укладка трубопровода па дпо траншеи может производиться при отсутствии обводнения траншеи, причем обводнение может быть уже после засыпки трубопровода грунтом. Укладка трубопровода в некоторых случаях может производиться и в обводненную траншею. В связи с этим в различный период действуют и различные сочетания нагрузок. В общем случае будем исходить из того, что обводненный грунт обладает определенной удерживающей способностью против поперечных вертикальных (вверх) перемещений трубы. Удерживающая способность определяется расчетом иа основании данных гидрогеологических изысканий и прогноза изменения физико-механических свойств грунтов, В ряде случаев исходя из возможной недостоверности исходных данных по грунтам, а также с целью обеспечения надежности трубопроводов больших диаметров, согласно нормам, «балластировка грунтом» не учитывается.
Прн укладке трубопровода на дно необводненной траншеи необходимо обеспечить проектное положение трубопровода, т. е соответствующие углы
поворота трубопровода в вертикальной плоскости прн ограничениях по из-гнбным напряжениям. Углы поворота трубопровода часто выполняете упругим изгибом трубопровода по действием собственного веса трубы. Исходя из этого, определяется профиль трубопровода. Для обеспечения устойчивости положения трубопровода в этом случае необходимо, чтобы выполнялось следующее условие:
где Бвят — интенсивность упругих сил; т — коэффициент условия работы-трубопровода; <?гр — расчетный вес единицы длины.
Интенсивность упругих сил может определяться в записимости от направления угла поворота по (9 28) или (9.37). Отметим, что 5рзг завис не только от угла попорота, но и уровня максимальных напряжений, ха растеризуемых минимальным радиусом упругого изгиба. Исходя из последнего vi ограничивается область применения упругого изгиба трубопровода для осуществления поворота трубопровода. Профиль траншей определяется в зависимости от угла поворота и минимального радиуса упругого изгиба оси трубопровода и может назначаться в соответствии с уравнениями (9.34) или (9 43). Если в соответствии с принятым в проекте углом поворота и минимальным радиусом упругого изгиба оси трубы условие (9 44) не выполняется, то для изгиба трубопровода он может лрнгружаться балластом. В этом случае условие (9.44) запишется в виде
Б изг < т fop + <?бал), (9.45)
где (?б«л — расчетная интенсивность поперечной нагрузки от балласта с учетом коэффициента перегрузки. Если до начала эксплуатации трубопровода возможно его обводнение, то устойчивость положения для этого периода проверяют по условию
^изг "т ^в. т ^ ?в. (^тр " ^бал ^ *?пр. гр\ (9.46)
где q„ т — расчетная интенсивность выталкивающей силы, действующей на трубу с учетом коэффициента перегрузки; qB о — расчетная выталкивающая сила, действующая на конструкцию балластировки с учетом коэффициента 1 перегрузки; qnр. гр — расчетное предельное сопротивление грунта поперечным вертикальным (вверх) перемещениям трубы, определяемое по (9,4— 9,6) с учетом коэффициента перегрузки, равного 0,8.
Левая часть условия (9.46) отражает интенсивность нагрузок, действующих в поперечном направлении оси трубопровода вверх, правая — вниз.
Отметим, что при расчете устойчивости положения на период последую-тцего (после укладки трубопровода в сухую траншею) обводнения траншеи в предэксплуатационпый период в <7сал включается также при наличии анкеров их удерживающая способность, определяемая по (9.13).
При укладке трубопровода в обводненную траншею устойчивость его положения на период строительства проверяют по условию
Бизг + 9в.т + 9в.<3^"г(?тр 9*1.). (947>
В отличие от предыдущего случая, здесь не учитывается удерживающая способность анкеров и грунта.
Прн укладке трубопровода в необводненную траншею и закреплении его анкерами повышенной несущей способности при последующем обвод- , нении в трубопроводе могут возникнуть значительные изгибные напряжения. В связи с этим необходимо произвести проверку против развития чрезмерных деформаций. Особенно это относится к участкам трубопроводов, имеющих упругий изгиб выпуклостью вверх. Условия для ограничения деформаций
где <7и ))н — максимальные продольные напряжения от нормативных нагрузок; — нормативный предел текучести металла труб.
При определении продольных напряжений для рассматриваемого периода считается, что пролет трубопровода равен расстоянию между анкерами, а р пролете действует соответствующая поперечная нагрузка, направленная вверх Кроме того, учитываются и продольные напряжения, связанные с упругим изгибом трубы по заданному профилю.
В записанных формулах, определяющих устойчивость положения трубопровода в период строительства (до эксплуатации), не отражены нагрузки, связанные с воздействиями деформаций грунта, сопровождающихся изменением его структуры, например пучение и др. При их наличии необходим расчет, учитывающий действие дополнительны»; нагрузок. Отмстим также, что здесь ие учитывается изменение температуры стенок трубы в течение времени от укладки трубопровода в траншею и засыпки его грунтом до начала эксплуатации трубопроводной системы. Обычно изменение температуры в этот период меньше, чем изменение температуры стенок труб, свя-чаиное с температурой транспортируемого продукта. Однако в некоторых случаях, например, если температурные перепады для периода строительства н эксплуатации отличаются по знаку, необходимо и для случая строительства проверять продольную устойчивость трубопровода.
Проверку продольной устойчивости трубопровода на обводненных участках можно производить по зависимостям, приведенным в гл. 5, принимая за предельное сопротивление поперечным перемещениям трубы равнодействующую всех поперечных нагрузок.
Трубопроводы, прокладываемые иа обводненных участках, имеющие углы поворота в вертикальной или горизонтальной плоскости, под действием продольных осевых усилий могут иметь большие перемещения. Для оценки их напряженно-деформированного состояния можно использовать программы для ЭВМ «Шаг — вода» и «Дога — вода»
§ 6. Расчет трубопровода с произвольным очертанием оси в горизонтальной плоскости
Для расчета подземных трубопроводов с произвольным очертанием оси в горизонтальной плоскости, прокладываемых на обводненных участках, можно использовать разработанную ВНИИСТом и ЮжНИИГипрогазом программу «Шаг —вода» (текст программы на машинных носителях хранится в организациях-разработчиках).
Программа «Шаг — вода» разработана в развитии программы «Шаг — лента». Остановимся только на особенностях алгоритма этой программы и отличиях его от ранее описанного. Области применения программ «Шаг — вата» и «Шаг — лента» идентичны, за исключением того, что алгоритм данной программы учитывает особенности работы трубопровода на обводненных участках трассы. Уровень грунтовых вод может быть различным по длине рассчитываемой конструкции. Подготовка исходных данных для расчета на ЭВМ но программе «Шаг — вода» проводится аналогично программе «Шаг —лента». Узлы стыковки элементов (узловые точки) должны дополнительно назначаться в местах изменения уровня обводнения, а также в местах изменения вида балласта и его величины Особенностью данной версии программы является более удобный для практических рас четоп ввод исходных данных, что позволяет уменьшить описание входной информации. Исходные данные для расчета по программе «Шаг — вода» заносятся на специальные двусторонние бланки, иа которых указаны обозначения данных, их физический смысл и размерность Первая строка бланка содержит информацию общего плана — наименование отдела (8 символов), заказа (4 символа), варианта (8 символов), даты (8 символов) и наименования объекта (ие более 52 символов). Во Вторую строку заносятся значения параметров, постоянных по длине рассчитываемого участка: k — число внутренних узлов; а — коэффициент линейного расширения материала труб; Е — модуль упругости материала трубы; ц — коэффициент Пуассон^ материала трубы; \Чр — объемный вес меча.ила, kn — коэффициент иадед ности, принимаемый по СНнП 11-45—75 Следующие величины в згой строк вводятся для расчета податливости трубопровода на левом и правом коц'? цах рассчитываемого участка в местах иодсоедиксния к прямолинейном^ участку магистрали: ?>в — наружный диаметр трубы магистрали; Ь --щина стенкн трубы магистрали; Л —высота засыпки под трубой магнстраЛ а — расстояние от трубы магистрали до стенки траншеи; А/ — расчети температурный перепад для магистрали; р — рабочее давление продук? для магистрали.
Если податливость заведомо известна иа том или другом конце рассч тыпасмого трубопровода, то приведенные величины для магистрали задайте»1 нулевыми. Третья н всс последующие строки лицевой стороны бланка разбиты иа вертикальные графы. Первая вертикальная графа указывает на* нумерацию участков (элементов). Вторая графа служит для нумерации пер-] фокарт. Последующие графы предназначены для задания техно.тогпчсскил параметров (At, р), геометрических Характеристик поперечного ссчення я" фнзико-механических характеристик металла труб (D„, б, 1, <р, р, с, А, «тр, &>в), типа грунта и различных его физико-механических характеристГ
(Фгр, Утр, Сгр,
Егр> 1*гр* Сх о» $гр).
Данные для второго участка (третья строка бланка) заполняются лм костью. Далее заполнение удобнее вести по графам. Во всех графах лицевой стороны бланка (кроме I. q> и тнпа грунта) исходные данные, в случае их повторения, не заносятся до появления в них числа, отличного от предыдущего. Нуль в этих графах недопустим. i
В первую строку оборотной стороны бланка заносится податливость упругих связей в начальной и конечной точках расчетной схемы (йл-, с2«-, Сзл-, ci к, С2к, Сзк). В последующие строки оборотной стороны бланка заносятся данные по обводнению — у>-, у», е, hB. яъ&л, q°ч„ и внешние обобщенные усилия — ZI, 22, Z% (изгибающие моменты, поперечные н продольные силы), приложенные в соответствующих узлах. Причем в первой точке (вторая перфокарта) величины, характеризующие обводнение, заменяются нулями. Для второго элемента (третья перфокарта) данные заполняются полностью. Начиная с третьего элемента, повторяющиеся величины в графах уу. у в и с, пс заполняются, а в графах Лв, <?сал, ^ачк заполняются все, кроме нулевых данных.
При заполнении бланков следует знать, что первая и вторая строки лицевой стороны и первая строка оборотной стороны заполняются только на первом листе
Перфорация исходных данных выполняется на перфокартах. Каждая строка бланка перфорируется на отдельной перфокарте. Первая строка содержит текстовую информацию, все последующие—цифровую. Порядок набивки листов: сначала все заполненные строки лицевых сторон бланков, затем оборотных в порядке их нумерации. В случае, если информация помещается более чем иа одном бланке (от одного до пяти), то первые две строки лицевой стороны бланка набиваются только е. первого листа, набивка последующих листков начинается с третьей строки. Третья строка набивается обязательно полностью с первой по 77-ю колонку. В следующих. строках набиваются только заполненные числа. Первая строка оборотной стороны избивается только один раз, и эта перфокарта ставится сразу после всех карт с. лицевых сторон бланков. Во второй строке первые шесть данных— обязательно нули, a Zt. Z?, Zs могут быть и не нулевыми Третья строка набивается полностью В остальных — только заполненные числа.
Выходная информация, получаемая по программе «Шаг — вода», аналогична выходной информации программы «Шаг —лента». Она содержит данные о всех компонентах напряжений н перемещений по длине рассчитываемого участка, значение усилий, действующих на примыкающие конструкции, а также сравнение вычисленных напряжений с предельно допустимыми, установленными нормами.
§ 7. Расчет трубопровода с произвольным очертанием оси в вертикальной плоскости
Для расчета подземных трубопроводов с произвольным очертанием оси в вертикальной плоскости можно использовать разработанную ВНИИСТом и ЮжНИИГнпрагазом программу «Дога— вода» (текст программы па машинных носителях хранится в оргаиизациях-разработчнках). Программа «Дога — вода» разработана в развитии программы «Дога». Остановимся только на особенностях алгоритма этой программы и отлячиях его от ранее описанного. Так как область применения программы распространяется на расчет трубопровода на обводненных участках, то алгоритм программы более полно учитывает отличие жесткостей, характеризующихся модулем деформации, грунта засыпки и основания (под трубой). Направление лоперечных перемещений (вверх или пннз) является неизвестным, поэтому в процессе счета анализируется характер перемещений и, в зависимости от направления, на каждом этапе счета учитываются соответствующие характеристики грунта. Отметим также, что алгоритм программы учитывает различие между балластировкой трубопровода грузами и закреплением его анкерами с точки зре-нггя их влияния на сопротивление продольным перемещениям
Подготовка исходных данных для расчета на ЭВМ по программе «Дога —вода» проводится аналогично программе «Дога». Узловые точки должны назначаться в местах изменения уровня обводнения, а также вида балласта и его величины.
Исходные данные для расчета заносятся на специальные бланки. На первую перфокарту заносится Информация об отделе, заказе и варианте (8 символов) и о наименовании объекта (не более 56 символов). На вто pvio перфокарту заносится число разбиений (не более 100) и признаки PRZX и PRZ2, характеризующие условия по концам трубопровода. На третью перфокарту заносятся параметры, постоянные по длине рассчитываемого участка: ро—рабочее (нормативное) давление; &( — температурный ле ррпад, DH — наружный диаметр трубопровода; а — коэффициент объемного расширения; Е— модуль упругости металла; ц, — коэффициент Пуассона ме талла; с — коэффициент, определяемый согласно СНиП П-45—75; m — коэффициент условия работы трубопровода; —коэффициент безопасности по материалу; ku — коэффициент надежности; пр — коэффициент перегрузки рабочего давления; /tirp, л2гр — коэффициент перегрузки для грунта.
После разбивки рассчитываемого участка на элементы информации
о геометрии заносится в перпый и второй столбцы четвертой и последующих перфокарт. Длина U заносится по порядку, начиная с левого конца. Угол поворота у,- между элементами образуется вращением продолжения предыдущего элемента к последующему. При вращении по часовой стрелке угол считается положительным, против — отрицательным. Знак минус записывается обязательно, знак плюс можно опускать. Углы задаются в градусах и десятых долях от них.
Па последней перфокарте записывается Y* +1=0. На четвертой н последующих перфокартах заносятся: 6 — толщина стенкн трубы; ft — высота засыпки нал трубой; R'{, R]>— нормативные сопротивления материала трубы растяжению (сжатию); PRGR=1 для песчаных грунтов и PRGR= О для глинистых грунтов; Yrp — объемный вес грунта; фгр — угол внутреннего трения грунта; стр — сцепление грунта; Егр. зас — модуль деформации грунта засыпки; Егр оси — модуль деформации грунта основания; ргр —коэффициент Пуассона грунта; сх о обобщенный коэффициент касательного сопротивления грунта; RTP — несущая способность грунта; —удельный пес грунта; у» — объемный вес воды с учетом растворспных солей и взвешенных веществ; е — коэффициент пористости; ftB — расстояние от верха засыпки до уровня воды, если уровень воды выше поверхности засыпки, то следует принимать Ао=0; ЦД1,п — расчетный (с коэффициентом безопасности по материалу) вес балласта под водой (задается со знаком плюс)
или расчетное усилие анкерного устройства на единицу длины (задает! со знаком минус).
Четвертая строка бланка заполняется полностью. В последующих стт/ ках все величины (за исключением I. у, PRGR, дяпВ) в случае их по^ рения можно не заполнять. Нулевые значения этих величин недопустим*
Выходная информация, получаемая по программе «Дога — вода», анэ* логична выходной информации программы «Дога». Она содержит дГ ные о всех компонентах перемещений н напряжений по длине расечн ваемого участка, результаты проверки прочности, деформативностн к у тойчивости трубопровода.
Алгоритм программы не учитывает предварительных напряжений в Tpj бопроводе, возникающих в процессе его укладки. Кроме того, при состав? лении данного алгоритма удерживающая способность анкеров или грузоИ учитывается как интенсивность, равномерная по длине элемента, что совсем потно отражает напряженное состояние трубопровода при прим| нении анкеров большой удерживающей способности, устанавливаемых значительным шагом. В этих случаях нужно дополнительно учесть nanpf жения от предварительного изгиба трубопровода и от нагрузок, действуй^ щих в пролете между анкерами.
Пример 1. Определить величину пригрузкн для выполнения угла повоЯ рота 1с30' в вертикальной плоскости с помощью вогнутой упругой кривой минимальным радиусом р=3000 м. Трубопровод 1420X16,5 мм, /=*1,79-
• 106 см*. ?=2,1 - 107 Н/см2. (.
Переводим угол в градусных единицах измерения в радианы
д яр° я1.5 „ „со
р = —-— —-= 0,0262 рад.
180 180
Прнгрузка по формуле (9.28)
Бнзг =, — . _2JJ0M179110f_ =7 н/см ^ ?20 н,м 9 0,0262®. (3-10»)®
Тапгенс по (9.32)
3
Т —0,0262-3000 = 58,95 м.
4
Биссектриса по (9.33)
Б = 0,141-0,02622 3000 = 0,29 м = 29 см.
Пример 2. Определить пригрузку для выполнения угла поворота 1°30' с помощью выпуклой упругой кривой мийнмалышм радиусом р =3000 м.
Трубопровод сечением 1420x16,5 мм. Угол поворота в радианах
180
Пригрузка по (9.37)
с 8 2,1-ЮМ ,79-10е
? изг —¦ *'— •--—' ’ — 1,8 Н/ см -— 180 11/м.
9 0,02622(3-10»)*
Тангенс по (9.41)
Г= 1,5-0,0262-3000= 117,9 м.
Пример 13. Для трубопровода 1420X16,5 мм (#тр=57 Н/см) определить предельный угол поворота, который можно выполнить упругим изгибом трубопровода иод действием собственного веса, чтобы минимальный радиус ск и изгиба трубы составлял 3000 м.
Для вогнутой кривой по (9.29):
В min —-— л / •—-—-—-—-—— - 9,32-ДО—3 рад;
3-3105 V 5,7-3-105-
180-9,32-10~3 Для выпуклой кривой по (9.38) :
й 2 /2-2,1- ЮМ,79-10*
Пример 4. Проверить устойчивость подземного участка трубопровода 1420X16,5 мм, проложенного упругим изгибом р=2500 м в вертикальной плоскости с углом поворота «=3,45° при рабочем (нормативном) давлении р=7,5 МПа и положительном температурном перепаде At —58°С.
Глубина заложения до верха трубы /г = 100 см, уровень грунтовых вод от верха засыпки hr, — 120 см. Грунт — песок средней крупности, объемный вес угр= 15,2 кН/мг, удельный вес уу=25 кН/м3, коэффициент пористости 8=0,5, угол внутреннего трения фгр=27°, сцепление сгр=0,05 Н/см2.
Определим предельное сопротивление поперечным перемещениям трубы вверх.
Площадь сечения стенок трубы
_ ."(ft, *%¦)_ _ лНгВЗL , 727 5 с«>.
4 4
Вес единицы длины трубы
<?т[) = /'YTp = 727,5 7,85-10~2 — 57 Н/см.
Вес продукта (газа) в единице длины трубы
9газ ~ ,00nnPDBH ¦= 100-0,95-7,5-1.3872 - 1370 Н/м = 13,7 Н/см.
Вес трубопровода
<утр =i 57 -f 13,7 = 70,7 Н/см.
По формуле (9.2)
а = 360' — 2 arecos -2i1-7i-IlI20L- _ 271,8°.
142
По формуле (9.1)
Foe. = -sin271.fi ) -1.45-10* см2.
Выталкивающая сила
9в = Гобв7в= 1,45-104-1,05-10-2= 152 Н/см.
Положительная плавучесть
Qh. т ^тр — Цвыт =~ 70,7 -— 152 — 81,3 Н/см.
2,5 10~Z— 1,05-1Q-
Твэв — •
(171 — 120)-142 -i-----1,45- 10* + 1 [1.52-№-*•120 X
X (2-171 — 120) tg (0,7 27)+0,9710 2 X 0,7 171 0,05
= 396 Н/см.
X (171 — i20is fg (0,7 - 27) +
cos (0,7 -27)
Сопротивление поперечным перемещениям
<7пр Я«. т + «rpVnp. гр ' - 81,3 + 0,8-396 _ 235,5 Н/см Коэффициент разгрузки
396
1,64 Н/см2.
+ ^RH 1422 4- 138 Тг
EI = EF—S———= 2,1- 107-725,7 —t———— — 3,75-Ю13 Нем®.
h + D„ 100 + 142
Иэгнбнзя жесткость грубы
Э2 ви
16 16
г _ <?пр гр
Ср ---
Принимая po=p. находим расчетную длину волны выпучивания по формуле (5.47):
]} =¦ кр
= 6,8-10’ см*;
250 000-235
,в(
V V (2,5-106-235,5)* J ?Кр = 8,13-Ш> см = 81,3 м.
265-3,75-10«
Длина хорды упругой кривой
п. Ч 4Ц
L0 = 2р sin —— = 2 2500 sin ———- 150,5 м.
2 2
Так как L0>LKv, то потеря устойчивости возможна на участке кривой, поэтому р= =<> и критическое продольное усилие, которое может воспринимать данный участок, определяется по формуле
NKр = 0,375дПг>Ро 0,375 • 235,5-2,5 • 10* = 2,2 -10? Н.
Определяем действующее эквивалентное продольное сжимающее усилие. Кольцевые напряжения
Усилие
S = (ссДtE + 0,2окц) F = (12-10-®-58-2,1 • 10» + 0,2-346,8)-727,5 =
= 1,57-10% МПа-см2 = 1,57-107 Н.
Проверяем предельное состояние по продольной устойчивости
S<mNK р, 1,57-10*<0,9-2,2-107, 1,57-10» < 1,98-107.
Таким образом, принятое конструктивное решение рассчитываемого подземного участка обеспечивает продольную устойчивость трубопровода
Пример 5. Определить шаг анкеров диаметром 400 мм (Л'авк=53 кН) из условия про; ольной устойчивости газопровода 1420X16,5 мм (<?тР= -5770 Н/м, /=1,79-10® см4), выполненного упругим изгибом р=4000 м с углом поворота а= 1°30', проложенного на болоте, подстилаемою мине-алышм грунтом — песками (ferp==2). Участок газопровода относится к III категории (т=0,9). Рабочее (нормативное) давление 7,5 МПа. температурный перепад Л/=60 °С
Вес единицы длины газопровода с продуктом
<?т. я = <?тр + пп- 100pD|H = 5770 + 0 95-100-7.5-1,387»=
= 7150 Н/м = 7,15 кН/м.
Допускаемая нагрузка на анкерное устройство по (9.14)
Ба„к-2-2,53-0,5= 106 кН.
Эквивалентное продольное сжимающее усилие
S^( 0,2 -Ы-7—..—8'—. . 12-10-6 2,1 -Ю»-6о\ 727= 160347 МПа-см*^
V 2-1,65 )
^ 1,6-10’ Н.
Предельное сопротивление поперечным перемещениям газопровода, обеспечивающее его устойчивость, определяется из (5.48)
а =-^-Ы—-- = 119 Н/см =11,9 кН/м.
^ 0,375р0т 0,375-4- 105-0,9
Выталкивающая сила воды, действующая на трубопровод, по (9.3) л¦1 42^
qu--¦ 10 500 16 900 Н/м = 16,9 кН/м.
Шаг анкеров из условий продольной устойчивости
^ __ Бенк___= 4 8 м
<?лр — <?т-п + <7в 11,90 —7,15-f-16,90
Проверяем условие возможности образования волны выпучивания на длине упругой кривой принимая в (5.47) ср=0:
= jgj.l-_10M,?.j» = , 10, ш;
кр 2-11,9-4-10»
Ецр 102,4 Mi
а 15°
La — 2р sin = 2-4000 sin—~—= 104 м;
L0>LKP; 104 >102,4.
Таким образом, необходимый шаг анкеров равен 4,8 м.
Пример 6. В качестве иллюстрации применения программы «Дога вода» приведен пример расчета подземного трубопровода с криволинейн^ в вертикальной плоскости осью, проложенного в обводненной траншее. ^
Трубопровод рассчитывается на внутреннее давление р=7,5 МПа d температурный перепад Л/=50 “С. Рассчитываемый участок выполнен из труб 1420X17,5 мм за исключением криволинейной вставки с углом 9°, тол шина стеики которой 6=19,5 мм. Угол поворота (вогнутый) равный 4°, выполнен упругим изгибом р=2500 м. Физико-механические характеристики металла трубы следующие. R* — 570 МПа, Rw2 ~ 470 МПа; иа участках 23Г 28 R* = 420 МПа. Высота засыпки над трубой меняется по длине труст провода р пределах 100—140 см, объемный вес грунта Yrr= 15; 17 кН/*а] угол внутреннего трения фгр = 19; 30°, сцепление сгр=0,003; 0,012 МПИ модуль деформации грунта засыпки ?гр яа'с =25; 38 МПа, модуль де-'J формации грунта основания ?гр. 0ся=35; 48 МПа, коэффициент Пуассон! грунта Цгр=0.12: о,22, коэффициент касательного сопротивления ?хо=0,02* 0,033 МПа/см, несущая способности грунта #гр=0,12; 0,15 МПа, коэффР ииент пористости 6=0,75. Расстояние от верха засыпки до уровня воды меняется по длине рассчитываемого участка в интервале 50—250 см. Для обес-' печения устойчивости положения трубопровода предусмотрена его батла-стировка утяжеляющими грузами и закрепление анкерными устройствами. Интенсивность дополнительной нагрузки изменяется от 0 до 140 Н/см (при закреплении анкерами в столбце «вес дополнительного груза» условно ста-i вится знак минус).
Разбивка рассчитываемого участка на элементы изображена на рис. 48. Длины элементов и углы между ними приведены п форме представления исходных данных Исходные данные для контроля ввода распечатываются (см. результаты, выдаваемые с ЭВМ).
На определенном расстоянии от крайних углов поворота считается, что трубопровод «защемлен». Алгоритмом программы это условие реализуется тз пиде значений усилий по концам. Поэтому контролем правильности выбора сечения, которое можно считать «защемленным», служат перемещения. В приведенном примере расчета в начале участка поперечное перемещен «ие имеет —22 порядок, продольное —6, в конце >частка соответетвеннИ •—21 и —6 порядок, т. е. перемещения рагшы нулю. Это показывает правильность принятых граничных условий. Из анализа распределения про-лольимх и поперечных перемещений и трубопровода по длине следует, что общая длина рассчитываемого участка в данном примере может быть уменьшена
Характер распределения перемещений по длине, полученный на основании расчета, показывает, что на первом угле поворота поперечные nepei мощения направлены вниз и их максима лная величина равна 2,46 см, Иа втором — поперечные перемещения направлены вверх и равны 4,2 см, на третьем — поперечные перемещения незначительны и не превышают 0,7 см. Отметим, что хотя первый угол поворота, равный 9°, больше вто-f рого, рапного 6°, поперечные перемещения иа последнем большие, что объ-'
Рнс 48 Схема рассчитываемого участка трубопровода с разбивкой на элементы
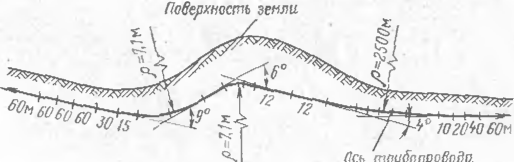
меняется меньшей жесткостью грунта засыпки по сравнению с основание^
Из рассмотрения результатов прочиостаото расчета следует, что наибольшие напряжения в растянутой зоне имеют место в 14 элементе, принадлежащем второму углу поворота, и равны 96,6 МПа. Наибольшие напряжения в сжатой зоне сечения имеют место на стыке 10 и 11 элемента, т. е. на участке первого угла поворота, н равны 129,1 МПа, допускаемые напряжения в сжатой зоне равны 227,3 МПа.
Построив эпюры перемещений, усилий и напряжений, можно судить
о характере работы рассчитываемого участка трубопровода
Выводы, полученные в результате расчета (см. пример), свидетельствуют о том, что принятое конструктивное решение удовлетворяет предельным состояниям, установленным нормами. Рациональное конструктивное решение можно выбрать методом вариантного проектирования различных схем прокладки и балластировки.
Пример 7. В качестве иллюстрации применения программы «Шаг — вода» рассмотрим расчет участка трубопровода типа шлейфа компрессорной станции, конфигурация которого в плане изображена «а рис. 49. Левая точка рассчитываемой системы принята неподвижной, т. е податливости ее трех связей — угловой, поперечной и продольной — приняты равными нулю. Справа рассчитываемый участок трубопровода примыкает к основной магистрали. Податливости этой связи вычисляются программно в соответствии с приведенными в гл. 6 расчетными формулами. В связи с этим введены исходные данные основной магистрали' трубопровод размером 1020X16 мм, высота засыпки над трубой 100 см, расстояние от трубы до стенки траншеи 24 см.
Шлейф характеризуется следующими параметрами. Трубопровод размером 1420X26 мм, углы поворота выполнены из отводов радиусом 150 см. Условно принято, что но длине рассчитываемого участка применены трубы с различными пределами текучести металла (/?” = 400 МПа, Я”=350ЛЩа). Гсмнературный перепад и внутреннее давление одинаково по длине и составляет Af=56,5°C, р—7,5 МПа.
Грунты по длине рассчитываемого участка различны: песок п сутли нок Физико-механические характеристики песчаного грунта объемный цес УгР = 19 кН/м3, угол внутреннего трення фГр=35°, сцепление сгр=0,001 Mila, модуль деформации грунта ?=30 МПа, коэффициент Пуассона грунта |'гр=0,25, обобщенный коэффициент касательного сопротивления i рун гг>
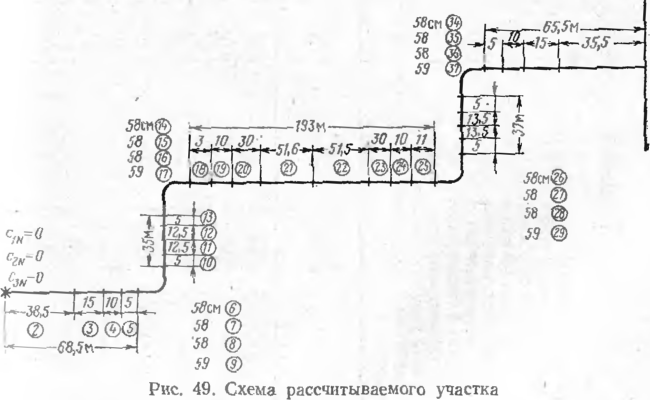
трубопровода на прочность и устойчивость в вертикальной плоскости с учетом обводнения ( «Дога — вода» )
27
Коэффициент Пуассона металла Удельный вес металла, кН/м3 Коэффициент условия работы Коэффициент безопасности по материалу
Коэффициент надежности Коэффициент перегрузки грунта
0.3
78,5
90
1.34
1.10
0.80
7,5 56 142 .000012 210 000 1.00
работы

1
2
3
4
5
6
7
8 9
10
11
12
13
14
6000.
6000
6000
6000.
6000
6000.
6000.
3000.
1500.
557.
557.
1200.
372.
372.
1.75
1.75
1.75
1.75 1 75
1.75
1.75
1.75
1.75
1.95
1.95
1.75
1.75
1.75
100.
100.
iOO.
J00.
;оо.
100.
юо.
120.
J20.
120.
120.
140.
140.
140.
570
570
570
570
570
570
570
5.70
570
570
570
570
570
570
470
470
470
470
470
470
470
470
470
470
470
470
470
470
0
0
0
0
0
0
0
0
0
О
0
О
0
О
17
17
17
17
17
17
17
17
17
17
.0017
.0017
¦0017
.0017
19.
19.
19.
19.
19.
19.
19.
19.
19
19.
19.
19.
19
19
.012
012
.012
.012
.012
.012
.012
.012
.012
.012
.012
012
012
012
Расчет подземного участка
Исходные данные:
Количество разбиений Левый конец защемлен Правый конец защемлен Нормативное давление, МПа Температурный перепад, °С Наружный диаметр трубы, см Коэффициент линейного расширения Модуль упругости металла, МПа Коэффициент, отражающий условия участка
0.0 0.0 0.0 00 0.0 00 0.0 00 -2.25 -4.50 —2.25 1 50 3 00 1.50
,
П р Д <> ji ж с \\ \\ I*.
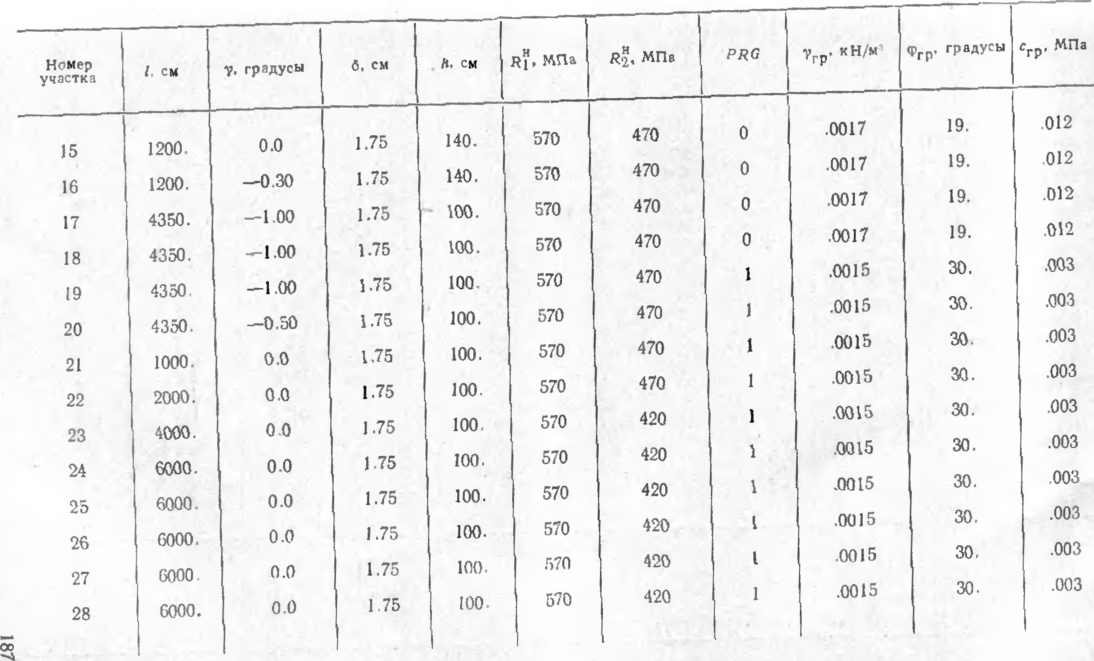
Номер
участка
'гр. зас МПа
гр- OCII'
МПа
^гр1
МПа
ГУД- ГР'
кН/м!
гр
1
2
3
4
5
6
7
8 9
10
и
12
13
14
15
16
17
18
19
20 21 22
23
24
25
26
27
28
25
25
25
25
25
25
25
25
25
25
25
25
25
25
25
25
25
25
38
38
38
38
38
38
38
38
38
38
35
35
35
35
35
35
35
35
35
35
35
35
35
35
35
35
35
35
48
48
48
48
48
48
4S
48
48
48
.12
.12
.12
.12
.12
.12
.12
.12
.12
.12
.12
.12
.12
.12
12
12
,12
12
.22
22
.22
.22
.22
.22
.22
.22
.22
.22
11 11 1 1 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11
| .033 | 15 |
28 |
| .033 |
.15 | 28 |
| .033 | 15 | 28 |
|
.033 | .15 | 28 |
| .033 | .15 |
28 |
| .033 | 15 | 28 |
| .033 |
.15 | 28 |
|
.033 | 15 | 28 |
| .033 | .15 |
28 |
| .033 | 15 | 28 |
| .033 |
.15 | 28 |
|
.033 | .15 | 28 |
| .033 | 15 |
28 |
| .033 | .15 | 28 |
| .033 |
.15 | 28 |
|
.033 | .15 | 28 |
| .033 | .15 |
28 |
| .033 | .15 | 28 |
| .022 |
.12 | 28 |
|
.022 | .12 | 28 |
| .022 | .12 |
28 |
| .022 | .12 | 28 |
| .022 |
.12 | 28 |
|
.022 | .12 | 28 |
| .022 | .12 |
28 |
| .022 | .12 | 28 |
| .022 | .12 | 28 |
| .022 | 12 |
28 |
X о* Mlla/см
к Н/м1
| е | /!ц, СМ | "бил- ИЛ' |
|
0.75 | 50. | —140 |
| 0.75 | 50. |
—140 |
| 0.75 |
50. | —140 |
|
0.75 | 50. | —140 |
| 0.75 | 50. |
—140 |
| 0.75 |
50 | —140 |
|
0.75 | 50. | —140 |
| 0.75 | 150. |
—120 |
| 0,75 |
150. | — 120 |
|
0.75 | 150. | -120 |
| 0.75 | 150 |
— 120 |
| 0.75 |
170. | 120 |
|
0.75 | 170 | 120 |
| 0.75 | 170. |
120 |
| 0.75 |
170. | 120 |
|
0.75 | 240 | —100 |
| 0.75 | 200. |
-100 |
| 0.75 |
200. | -100 |
|
0.75 | 200. | -100 |
| 0.75 | 200. |
—100 |
| 0.75 |
200. | —100 |
|
0.75 | 2.50. | 0.0 |
| 0.75 | 250. |
00 |
| 0.75 |
2.50. | 0.0 |
| 0 75 | 250. | 0.0 |
| 0.75 | 250. |
0.0 |
| 0.75 |
250. | 0.0 |
|
0.75 | 250. | 0.0 |
Результаты расчет«1
Изгибающий момент, Н см
Номер
участка
Координаты
Продольное усиЛ'Дг, Н
Попеп<?чнни сила, II
Попсрсч нос прри',ещети‘, см
Продольное перемещение, см
оо
0.5 1.0 0.0 0.5 1.0 0.0 О 5 1.0 0.0 0.5 1.0 0.0 0.5 1.0 0.0 0.5 1.0 0.0 0.5 1.0 0.0 0.5 1.0 00 05 I 0 0.0 0.5
1
1 1
2 2 2 3 3
3
4 4
4
5 5
5
6 6 6 7 7
7
8 8 8 9 9
9 10
10
00
01
03
03
04
05 05
05
06 06 06 07 07 07
02
03
04 04
04
05
05 04
06 07 06
00
00
00
01
01
01
00
00
00
00
00
00
—.7450Е—15 0.6012Е—13 0.6012Е—13 —.8622Е—12 0.1239Е—10 0.1239Е—10 —.4038Е—09 —.2420Е—07 .—2420Е—07 0.2584Е— 05 —.3710Е—'04 —.3710Е—04 —.74 06Е—02 0.4841 Е 00 0.4841Е —.6806Е 0.1000Е 0 1000Е —.1440Е 0.2027Е 0.2027Е 0.240GE —.3917Е —.3917Е —.7067Е 0.1003Е 0.1003Е 0.1357Е
| —.3329Е | 07 |
| 3329Е |
07 |
| —.3329Е |
07 |
| —.3329Е |
07 |
| —.3329Е |
07 |
| — .3329Е |
07 |
| —.3329Е |
07 |
| —.3329Е |
07 |
| — .3329Е |
07 |
| —.3329Е |
07 |
| —.3329Е |
07 |
| —.3398Е |
07 |
| — .3328Е |
07 |
| — 3326Е |
07 |
| — .3322 Е |
07 |
| —3322Е |
07 |
| .—3312Е |
07 |
| .-3286Е |
07 |
| —.3286Е |
07 |
| — .3224Е |
07 |
| —.3069Е |
07 |
| —.3069 Е |
07 |
| —.2921Е |
07 |
| —.2687Е |
07 |
| —.2687Е |
07 |
| — .2525Е |
07 |
| —.2321Е |
07 |
| — 2384Е |
07 |
| —.2322Е |
07 |
0.0
— .2117Е—15 0.6168Е—14 0.6168Е—14 -.9458Е—13 0.1501Е—11 0-1301Е—11 0.1Э07Е—10 —.8371Е—08 —.8371Е—08 0 3306Е—06 0.1396Е—04 0.1396Е—04 0.1837Е—02 0.3789Е—01 0.3789Е—01 —.6660Е—00 0.1094Е 02 0.1094Е —.1742Е 0.2698Е 0.2698Е —.4907Е
— .5341Е
— .5341Е
— .8733 Е 0.5179Е
—.6765Е 0.2902Е
0.1097Е—22 —.5222Е—21 —. 1226Е—19
— 1226Е—19 —-1419Е—18
0 4610Е—17 0-4610 Ё—17 0-3837Е—15
— .2438Е—13
— 2438Е—13 —-2916Е—12
0-9610Е—10 0.96ШЕ-10 —.3857Е— 08 .—1574Е—06
— -1574Е—0в 0 3149Е—06 0 1607Е—04 0.1607Е—04
—.5309Е— 03 0 1186Е—01 0 1188Е-01
— 1010Е 00 —.14G2E —.1462Е
0.4807Е 0.1883Е 0.1889Е 0.2295Е
0 .6894Е -06 0.3471 Е—05 0.7584 Е—05 0.0
0.4161 Е—05 0.1 ЮЗЕ-04 0.6894 Е—05 0Л795Е—04 0.4481 Е-04 0.3723Е—04 О 9586Е—04 0.2385Е—03 0.2337Е—03 0.5791Е—03 0.1431Е—02 0 1427Е—02 0.3528Е—02 0.87I6E—02 0.8716Е—02 0.2152Е—01 0.5318Е—01 0.5318Е—05 0.8359Е—01 00
0.1314Е
0.1314Е
0.1647Е
0.2065Е
0.1324Е
0.1670Е
Номер
участка
Изгибающий Момент. Нем
Продольное усилие, Н
Координаты
Поперечная енла, Н
Поперечное перемещение, см
Продольное перемещение, см
ю
11
))
и
12
12
12
13
13
13
14 14
14
15 15
15
16 16 16 17 17
17
18 18 18 19 19 19
1 0 00 0.5 1.0 0.0 0.5 1.0 0.0 0.5 1.0 0.0 0.5 1.0 0.0 0.5 1 0 0.0 0.5 /О 0.0 О 5 1.0 00 0.5 J.0 0.0 0.5 1.0
0.2749Е 07 0.2748Е 07 0.1987Е—01 О 21 ЭЕ 07 0.219Е 0.25I0E
— .2282Е —.2282Е —,2688В —.3285Е
— .3285Е —.2652Е
— .2210Е
— .221ОЕ 0.1286Е 0.8699Е 0.8699Е О 6465Е О 5227Е 0.5227Е
— .1717Е 0.6920Е 0.6920Е
—.1948Е 0.6534Е 0.6535Е —Л409Е ОШОЕ
| —.2247Е | 07 |
| —.2256Е | 07 |
| —.2244Е | 07 |
| —.2218Е | 07 |
| —.2163Е | 07 |
| —.2126Е | 07 |
| — 2049Е | 07 |
| — .2057Е | 07 |
| — 2050Е | 07 |
|
— .2038Е | 07 |
|
— 2037Е | 07 |
|
—.2081Е | 07 |
|
—.2192Е | 07 |
|
— 2113Е | 07 |
|
— .2319Е | 07 |
|
—.2475Е | 07 |
|
-.2475Е | 07 |
|
—¦261 IE | 07 |
|
—.2794 Е | 07 |
|
—.2724 Е | 07 |
| - .3000Е | 07 |
|
— .3130Е | 07 |
| .—3130Е | 07 |
|
—.3215Е | 07 |
|
—-3251Е | 07 |
|
— .3251Е | 07 |
|
—.3275Е | 07 |
|
— .3284Е | 07 |
| 0 6975Е | 06 |
| —.4643Е |
06 |
| —.6330Е |
05 |
| 0.2635Е |
06 |
| —.3156Е |
06 |
| —,2620Е |
06 |
| —.5053Е |
06 |
| -Л220Е |
06 |
| — .2365Е |
06 |
| — 3635Е |
06 |
| 0.4023Е |
06 |
| 0.2804Е |
06 |
| 0.1615Е |
06 |
| 0.5465Е |
06 |
| 0.1840Е |
06 |
| 0.1350Е |
05 |
| 0.1350Е |
05 |
| — .7897Е |
05 |
| 0.4073Е |
05 |
| —.9287Е |
05 |
| —.4782Е |
04 |
| 0.1373Е |
06 |
| — .1369Е |
06 |
| 0Л 764Е |
04 |
| 0.1230Е |
06 |
| —. 1534 Е |
06 |
| O.J478E |
04 |
| 0 1379Е |
06 |
0.2448Е 0.2455Е 0.2204Е 0.1589Е О 1591Е —.8144Е
— 3403Е —.3405Е —.3918Е
— 4196Е
— 4Г93Е —4205Е —3985Е
— 39S0E —.2375Е
— .7657Е —.7657Е
0.1359Е О 4407Е 0.4397Е
— .3959Е—02 0,7521Е 00 0.7516Е 00
—.1Э74Е—01 0.6347 Е 00 0.6345Е 00
— .4731Е—01 0.5442Е 00
01
01
01
01
01
00
01
01
01
01
01
01
01
01
01
00
00
00
00
00
0.2026Е 00 0.9986Е—02 0.4612Е—01 0.8255Е—01 0.2009Е—01 0.6389Е—01 О.1097Е 00 0.2067 Е—01 0.3533Е—01 0.5010Е—01 —.1696Е 00
— .1550 Е 00 —.1409Е 00 —.2452Е 00 —.2039Е 00 —-1692Е 00 —.I692E 00
— 1402Е 00 —.П57Е 00 -.1I96E 00
— .5905Е—01 —.2479Е—01 —.3791Е—01 —. 1762Е—01
— .5186Е—02 —. 1626Е—01
— .7594Е-02 —.1155Е—02
07
06
07
07
07
07
07
07
07
07
Об
06
06
06
06
06
06
06
06
06
06
06
06
06

П р о Д о л ж I' u и е
| Номер участка |
Координаты |
ИзгнбающнП | момент. Н-см |
Продольное усилие, Н |
Понерсчиля сплз, |
Поперечное переменен нс, см |
Продольное перемещение, ем |
| 20 20 20 21 21 21 22 22 22 23 23 23 24 24 24 25 25 25 26 26 26 27 27 27 28 28 28 | 0.0 0.5 1.0 0.0 0.5 1.0 0.0 0.5 1.0 0.0 0.5 1.0 0.0 0.5 1.0 0.0 0.5 1.0 00 0.5 1.0 0.0 0.5 1.0 0.0 0.5 1.0 | 0.6160Е 06 —.9335Е 05 0.2602Е 06 0.2601 Е 06 ¦—.1632Е 05 —.64G8E 05 — .6458Е 05 — 1928Е 05 0.3677Е 04 0.3677Е 04 — .1741Е 03 0.7254 Е 01 0.8211Е 01 —.2811Е 00 — .2316Е— 01 — .5061Е-03 0.531 ЗЕ 04 —.2798Е—05 ¦—.2563Е -05 0.1335Е—07 0.9041Е—07 0.3166Е—09 —.2122Е—11 — .2766Е—11 — 3624Е—13 0.1300Е—14 — .1305Е—16 | —.3284 Е 07 — .3302 Е 07 —.ЗЗПЕ 07 —.3311Е 07 — .3313Е 07 — .3315Е 07 — 3315Е 07 — 3318Е 07 —3320Е 07 — 3320Е 07 —.3324 Е 07 — 3326Е 07 —.3326Е 07 — .3327Е 07 — .3328Е 07 — .3328Е 07 .—3329Е 07 —.3399Е 07 —.3329Е 07 — 3329Е 07 —.3399F. 07 —.3329Е 07 —.3329Е 07 —.3329Е—07 —.3329Е 07 — .3329Е 07 — .3329Е 07 | —Л390Е 06 0 6955Е 04 0 5146Е 05 — .8726Е 05 — .2414Е 05 0.4177Е 04 0.4177Е 04 0.4066Е 04 0.7602Е 03 0.7603Е 03 —.4074 Е 02 0.2304Е 01 0.2174Е 01 0.5749Е—01 — 1953Е—01 — Л799Е— 03 — .8638Е—06 0.1816Е— 06 0.2396Е—06 —.6839Е—08 —.4656Е—08 —.2558Е—10 0.8602Е—12 0 1421Е—12 0.2948Е—14 —Л827Е—15 —.10S4E—17 |
0.5441Е 00 — 2554Е—01 0.1770 Е 00 0.1770Е 00 O.iOolE 00 0 314ЭЕ—01 0 3149Е—01 —. 1423Е—01 —.5036Е—02 —.5036Е-02 0.2563Е—03 —.1357Е—04 —. 1304Е—04 —.5U3E—07 0.1711Е-07 0 2064Е—08 —.4823Е—10 — .2995Е—13 0 6056Е—Г2 0.1505Е—13 —.7637Е—13 —.8997E-1G —.1911Е—17 0.2200Е—17 0.1280Е—19 0 Л 977Е—21 — Л621Е—21 |
—.1065Е—01 —.5944—02 —.2982Е—02 — .4578Е—02 —.4940Е—02 — .3561-02 —.3540 Е—02 —.2757Е-02 —.2140Е—02 —.2162 Е—02 —Л317Е-02 —.8037Е—03 —.8071Е-03 —.Г4836Е—03 — Л788Е—03 — .18G0E—03 —.8637Е-04 —.3745Е—04 — .4349Е—04 —.1870Е—04 —.4833Е—05 —Л987Е—04 —.2999Е—05 0.2416Е—05 —.3624Е—05 0.6257Е—Об 0.2416Е—05 |
| Номер участка |
Координаты | стпр N' | МПа |
[апр jV]' | МПа | <ТПР1, МПа | (°пр 1 ]• | МПа |
<тлр2, МПа | 1спр *]’ | МПа | ||
|
1 1 1 | 0.0 |
0.221 Е | 02 | 0.348Е | 03 | —.431Е |
02 | 0.192Е | 03 |
— .431Е | 02 |
0.192Е | 03 |
|
0.5 | 0.221Е | 02 |
0.348Е | 03 |
—-431Е | 02 | 0.I92E | 03 | —.431Е |
02 | 0.192Е | 03 |
|
| 1 0 | 0.221 Е |
02 | 0.348Е | 03 |
— -431Е | 02 | 0 192Е | 03 | — .431Е |
02 | Q.192E | 03 | |
| 2 | 0.0 |
0.221Е | 02 | 0.348Е | 03 | —.431Е |
02 | 0.192Е | 03 |
—.431Е | 02 |
0.192Е | 03 |
| 2 Л | 0.5 | 0.221Е |
02 | 0.348Е | 03 | -.431Е | 02 |
0.192Е | 03 | —.431Е | 02 | 0.192Е |
03 |
| 2 | 1 0 | 0.221Е | 02 | 0 34SE | 03 | —.431Е |
02 | 0.I92E | 03 | —.431Е | 02 |
0.192Е | 03 |
| 3 | 0.0 | 0.221Е |
02 | 0.348Е | 03 |
—.431Е | 02 | 0 192Е | 03 | — .431Е |
02 | 0.192Е | 03 |
| 3 | 0.5 |
0.221 Е | 02 | 0.348Е | 03 | —.431Е |
02 | 0.192Е | 03 |
—.431Е | 02 |
0.192Е | 03 |
| 3 А | 1 0 | 0.221Е | 02 | 0.348Е |
03 | —.431Е | 02 |
0.192Е | 03 |
—.431Е | 02 | 0.192Е | 03 |
| 4 А | 0.0 | 0.221Е | 02 | 0.348Е |
03 | — .431 Е | 02 |
0 192Е | 03 |
—.431Е | 02 | 0.192Е | 03 |
| 4 А | 0.5 | 0.221 Е | 02 | 0.348Е |
03 | —.431Е | 02 |
0.192Е | 03 |
—.431Е | 02 | 0.192Е | 03 |
| 4 г | 1 0 | 0.221Е |
02 | 0 348Е | 03 |
—.431Е | 02 |
0.192Е | 03 | -.431Е | 02 | 0.192Е |
03 |
| О г |
0.0 | 0.221 Е | 02 |
0.348Е | 03 |
—-431Е | 02 | 0.192Е | 03 | —.43IE |
02 | 0.192Е | 03 |
| 5 г | 0.5 |
0.221Е | 02 | 0.348Е | 03 | —.431Е |
02 | 0.192Е | 03 |
—.431Е | 02 |
0.192Е | 03 |
|
О с | 1.0 |
0.221 Е | 02 | 0.348Е | 03 | -.430Е |
02 | 0.192Е | 03 |
—.430Е | 02 |
0.192Е | 03 |
|
о ? | 0.0 | 0.221 Е | 02 | 0.348Е |
03 | -.430Е | 02 |
0.192Е | 03 | -.430Е | 02 | 0.192Е |
03 |
| О ft |
0.5 | 0.221 Е | 02 |
0.348Е | 03 | -.429Е | 02 | 0 I92E |
03 | —.429Е | 02 |
0.192Е | 03 |
|
и 7 | 1.0 | 0.221 Е | 02 | 0.348Е |
03 | —,426Е | 02 |
0.192Е | 03 |
—.426Е | 02 | 0.192Е | 03 |
| 1 7 | 00 0.5 |
0.221 Е | 02 | 0.348Е | 03 | —Л26Е |
02 | 0.192Е | 03 |
-426Е | 02 | 0.192Е | 03 |
| / 7 | 0.221Е | 02 |
0.348Е | 03 | —.417Е | 02 | 0.192Е |
03 | -.418Е | 02 |
0.192Е | 03 | |
|
/ о | 1.0 | 0.221Е | 02 | 0.348Е |
03 | —.390Е | 02 |
0.192Е | 03 |
—.405Е | 02 | 0.192Е | 03 |
| О О | 0.0 0.5 1.0 |
0.221Е | 02 | 0.348Е | 03 | — .390 Е |
02 | 0.192Е | 03 |
—.405Е | 02 |
0.192Е | 03 |
|
о 8 0 | 0.221Е |
02 | 0.348Е | 03 |
—.369Е | 02 |
0.192Е | 03 | —.387Е | 02 | 0.192Е |
03 | |
| 0 221Е |
02 | 0.348Е | 03 |
—.201Е | 02 |
0.192Е | 03 | —.495Е | 02 | 0.192Е |
03 | ||
| У Q |
0.0 | 0.221Е | 02 |
0 348Е | 03 | -.201Е | 02 | 0.192Е |
03 | —.495Е | 02 |
0.192Е | 03 |
|
У Q | 05 | 0.221 Е | 02 | 0.348Е |
03 | — .628Е | 01 |
0.192Е | 03 |
—.592Е | 02 | 0.192Е | 03 |
| У 10 10 | 1.0 | 0.221 Е | 02 | 0.348Е |
03 | 0.747Е | 01 |
0.427Е | 03 |
—.676Е | 02 | 0.192Е | 03 |
| 0.0 |
0.494Е | 01 | 0.348Е | 03 | 0.978Е |
01 | 0.427Е | 03 |
-.653Е | 02 | 0.227Е | 03 | |
| 0.5 |
0.494Е | 01 | 0.348Е | 03 | 0.237Е |
02 | 0.427Е | 03 |
—.779Е | 02 |
0-227Е | 03 | |
П р о д о л ж с и и е
•~о
|
01 _—- ti и Номер участка | Координаты | °пР N’ МПа |
[°лр*]-МПа | | °пр 1’ МПа | 1«прг]-МПа | %р а* мш | ["ар «1'МПа |
| ОС IO 10 11 11 11 12 12 12 13 13 13 14 14 14 15 15 15 16 16 16 17 17 17 18 18 18 19 19 19 20 3 СО | 1.0 0.0 0.5 1 0 0 0 0.5 1 0 00 0.5 1 0 00 0.5 1.0 0.0 0.5 1.0 0.0 0.5 1.0 0 0 0.5 1 0 0.0 0.5 1.0 00 0.5 1.0 0.0 | 0.494 Е 01 0.494Е 01 0.494Е 01 0 4 94 Е 01 0.221Е 02 0.221 Е 02 0 221Е 02 0 221Е 02 0.221 Е 02 0.221Е 02 0 221Е 02 0 221Е 02 0.221Е 02 0.221Е 02 0.221Е 02 0.221Е 02 0.221 Е 02 0.221Е 02 0.221Е 02 0.221Е 02 0.221Е 02 0.221Е 02 0.221 Е 02 0.221Е 02 0.221Е 02 0.221Е 02 0.221Е 02 0.221Е 02 0.221 Е 02 |
0 348Е 03 0.348Е 03 0.348Е 03 0.348Е 03 0.348Е 03 0.348Е 03 0.348Е 03 0.348Е 03 0.348Е 03 0.348Е 03 0.348Е 03 0.348Е 03 0.348Е 03 0.348Е 03 0.348Е 03 Q.348E 03 0.348Е 03 0.348Е 03 0.348Е 03 0.348Е 03 0.348Е 03 0 34 8Е 03 0.348Е 03 0.348Е 03 0.348Е 03 0.348Е 03 0.348Е 03 0.348Е 03 0.348Е 03 | 0.767Е 02 0.766Е 02 0.482 Е 02 0 564Е 02 0.542Е 02 —.181Е 02 0.588Е 02 0.587Е 02 0.740 Е 02 0.965Е 02 0.966Е 02 0.723Е 02 0.552Е 02 0.553Е 02 0.261 Е 02 0.471 Е 00 0.472Е 00 — 966Е 01 —.157Е 02 — .I57E 02 —.324Е 02 —.146Е 02 —.146Е 02 —.344Е 02 — .176Е 02 —Д76Е 02 .372 Е 02 —.195Е 02 .195Е 02 | 0.427Е 03 0.427Е 03 0.427Е 03 0.427Е 03 0.427Е 03 0.192Е 03 ОЛ27Е 03 0.427Е 03 0.427Е 03 0.427Е 03 0 427Е 03 0 427Е 03 0.427Е 03 0 427Е 03 0.192Е 03 0.427Е 03 0.427Е 03 0.192Е 01 0 192Е 03 0.192Е 03 0192Е 03 0.192Е 03 0.192Е 03 0192Е 03 0.192Е 03 0.192Е 03 0.192Е 03 0.192Е 03 0 192Е 03 |
—.129Е 03 —.129Е 03 — 100Е 03 — .108Е 03 — .110Е 03 — 369Е 02 —.112Е 03 —.112Е 03 — 127Е 03 — .149Е 03 — 149Е 03 —. 126Е 03 —.110Е 03 —.110Е 03 —.347Е 02 —.646Е 02 — .646Е 02 — .580 Е 02 ' —.549Е 02 ' — .549Е 02 — .453 Е 02 —.665Е 02 — .665Е 02 — .490Е 02 —.666Е 02 —.666Е 02 —.477Е 02 — 656Е 02 — .656Е 02 | 0.227Е 03 0.227Е 03 0.227Е 03 Q.227E 03 0.192Е 03 0 192Е 03 0.192Е 03 0.192Е 03 0.192Е 03 0 192Е 03 0.192Е 03 0.192Е 03 0.192Е 03 0 192Е 03 0 192Е 03 0 192Е 03 0.192Е 03 0.192Е 03 0192Е 03 0.192Е 03 0192Е 03 0 192Е 03 0 192Е 03 0.192Е 03 0.192Е 03 0-192 Е 03 0 192Е 03 0.192Е 03 0 192 Е 03 |
Продолжение
COCOCOCOCOCOCOCOCOCOCOCOCOCOCOCOCOCOCOCOCOCOCOCOCOCO
оооооооооооооооооооооооооо
шшшшшшшишшниышиившишишщымш
СМСМСМСМСМСЧСМСМСОСОСОСОСОСОСОСОСОСОСОСОСОСОСОСОГЧСО
cr>a^cr>c^cr>(^cr?c^cococOcocococococococococociococoU.)co
ОООООООООООООООООООООООООО
WWWWWWWUWWWWUJWWW
‘ОСОСОСОСОСОСОСОСОСОСОСОСОСОСОСО
СМ<МСМ(МСМ<МСМ<М<М<М<МСМСМ<МСМ(М
оооооооооооооооо
СОСОСОСОСОСОСОСОСОСОСОСОСОСОСОСОСОСОСОСОСОСОСОСОСОСО
оооооооооооооооооооооооооо
ЩШШШИЩИШШШШШШМШИШШИИИИШШШШ
С^СМСМСМСМСМ<М<МСОСОСОСОСОСОСОСОСОСОСОСОСОСОСОСОСОСО
ООООООООСОСОСОСОСОСОСОСОСОСОСОСОСОСОСОСОСОСО
ОООООООООООООООООООООООООО
С
смся
оо
<N СМ
оо
<МСМ
о о
СМ <М
оо
CM СМ
о о
с
?
ыш
ою <м со
щщ
TP TJ"
Ю LO
тт
шш
со о о см -чг ю
ишшш
5 СО СО н <Г 'Ф
с
й
| CM CV |
сч | сч | сч | счсч | СЧ |
СЧСЧ | сч | сч | см | сч сч |
сч см сч | счсчсч |
сч сч | счсч | сч |
| ОО | о |
о | о | оо |
О | оо | о | о | о | оо | ООО | ООО |
оо | оо | о |
| ШШ | W |
Ы | U4 | WW |
ш | Ш ш | ш |
ш | ш |
ШШЫ | ышш | адш | ш ш | ы | |
| СО СМ | О} | со | ю | »0 СО |
ст> | о —. |
•—< | г—1 |
т—* •—1 | --. _ __| |
.—. _ч | *—1 •—» |
|||
| о со | со | см | о | О см | см | (М со |
со | со | со | СО СО | со СО СО |
СО со СО | со СО |
со со | со |
|
СОСО | со |
-т | т* гГ | -«г | тг ТГ | гг |
^*1 | ^ г5! |
-ф -**< гг | -<г <г |
<г |
I I I I I I I II I I I I I I I И I I I I I I I I
СОСОСОСОСОСОСОСОСОСОСОСОСОСОСОСОСОСОСОСОСОСОСОСОСОСО
с
?
а
U
О
Выводы.
Конструкция удовлетворяет условиям прочности.
Конструкция удовлетворяет условиям по деформациям. Конструкция удовлетворяет условиям продольной устойчивости.
с
ё
с
ОООООООООООООООООООООООООО
OOOOOOQOoOOOcOOOoOCOoOoOOOQOOOQOQOOOOOQOOOOOOOoOOOoO
СОСОСОСОСОСОСОСОСОСОСОСОСОСОСОСОСОСОСОСОООСОСОСОСОСО
ОООООООООООООООООООООООООО
СЯСЯСЧСЯСЯСЧСЯСЯСЯСЧСЯСЯСЧСЪСЧСЧСЧСЯСЯСЯСЯСЧСЯСЧСЯСЯ
ОООООООООООООООООООООООООО
^^^СМС^СМ^^С^СМСМС^С^СМСЧСЧСЧС^С^С'ЗСМСЧС^СЧС^С^
CNCMC^CMCMCMCMCMCMCMC'iCMCMC^CNCMOgc'JCMCMCMC'iC'JCMC'JCM
ОООООООООООООООООООООООООО
ЮОО^ООЮОО'ООО^ОО'ООО^ООЮООЮ о О—*00^00 — 00^00-^00 —«ОО—«ОО-^ОО-ч
А V-
о ? ? о
о <Я
^0^,„^oj(N(NcOCOCO't'!l,4tiClflU5^)cDCDNNNOOQOCO
OjCMC'JCNCMCMCMCMCMCMCMC'ICMC'JCKMCMC'iCMCNCMCMCMCMCMCM
Cm = 0,02 МПа/см, несущая способность грунта йгр=0,4 МПа. Те же характеристики для суглинка:
УгР=16 Н/м\ фгр =22°, сГ1>=0,028 МПа, ?гр = 19 .МПа,
^гр—0,4, с*о 0,03 МПа/см, /?1Р=0,02 МПа.
Уровень воды (от верха засыпки) принят переменным и равным от 20 до 300 см. Удельный вес грунта принят равным 28 кН/м3. Удельный вес воды у* = П кН/м3, пористость грунта е=0,75. На части участков предусмотрена балластировка с помощью грузов <7оал = 140 Н/см, <?«» л
120 Н/см, иа ряде других анкерами, так что сопротивление qайк —100 Н/см.
Рассчитываемый участок разбит на 40 элементов, причем каждый отвод — На 4 элемента. Длина элементов и углы между ними приведены
в информации, выдаваемой ЭВМ.
Первая часть распечатки информации содержит исходные данные, вторая часть результаты расчета и третья часть — прочностной расчет. Про
анализируем полученные результаты. Из вывода следует, что принятое конструктивное решение удовлетворяет предельным состояниям, установленным нормами. Далее получаем нагрузки на примыкающие конструкции. На неподвижную опору действует изгибающий момент, равный М 0,477 ¦
• Ю5 Н-м поперечная сила, равная Q=500 Н, н продольное усилие N = =0,386-10 Н На примыкающий трубопровод действуют М=0 129-10‘ Н-м, Q=590 Н, N=0,517 • 107 Н.
Перемещения, действующие в тройииковом соединении, составляют: поперечное— 0,23-10-2 см, т. е практически нуль; продольное (ноперечное относительно магистрали) — 0,81 см, т. е. значительно меньше толщины тройника. Наибольшие изгибающие моменты и перемещения возникают в отводах, образующих угол поворота Во всех сечениях напряжения не превышают предельно-допустимых Например, в седьмом элементе напряжения в растянутой зоне — 202 МПа при пределыю-допустимы: 283 МПа,
в сжатой зоне — 26 МПа при предельно-допустимых 90,7 МПа
На основании приведенных результатов можио построить эпюры напряжений и перемещений, по которым проектировщик может представить себе характер работы трубопровода.
Расчет подземного участка трубопровода с произвольным очертанием оси в горизонтальной плоскости
с учетом обводнения ( «Шаг — вода» )
Исходные данные:
Расстояние от трубы до стенки траншей справа, см 22
р0< МПа
Д/. 'С
в, см
I, см
V, градусы
р, с к
А. см
Номер
участка
2
3
4
5
6
7
8
9
10 11 12
13
14
15
16
17
18
19
20
7.5
7.5
7.5
7.5
7.5
7.5
7.5
7.5
7.5
7.5
7.5
7.5
7.5
7.5
7.5
7.5
7.5
7.5
7.5
56.5
56.5
56.5
56.5
56.5
56.5
56.5
56.5
56.5
56.5
56.5
56.5
56.5
56.5
56.5
56.5
56.5
56.5
56.5
142.
142.
142.
142.
142.
142.
142.
142
142
142.
142.
142.
142.
J42.
142.
142.
142.
142
142,
2.60 2.60 2.60 2.60 2.60 2.60 2.60 2.60 2.60 2.60 2.60 2.60 2 60 2.60 2.60 2.60 2.60 2.60 2.60
3850.
1500
1000
500
58.
58.
58.
59. 500.
1250.
1250.
500.
58.
58
58.
59. 500.
1000.
3000.
0.0
0.0
0.0 -11.25 -22.50 -22.50 -22.50 -11.25 0.0 0.0 0.0 11 25
22.50
22.50
22.50 11.25 0.0 00 0.0
100Е 21 Л00Е 21 100Е 21 -100Е 21 .150Е 03 . 1 БОЕ 03 . 150 Е 03 .150 Е 03 . 100Е 21 .100Е 21 . 100 Е 21 100 Е 21 150Е 03 .I50E 03 -150Е 03 .150Е 03 0.100Е 21 Л00Е 21 Л00Е 21
0.85
0.85
0.85
0.85
0.85
0.85
0.85
0.85
0,85
0.85
0.85
0.85
0.85
0.85
0.85
0.85
0.85
0.85
0.85
100.
100,
100.
100.
100.
100.
100
100,
100.
100.
100.
100
100.
100.
100.
100.
100.
100.
100.
Продолжении
| Номер участка | р„, МПа | Aii 'С |
Ян, см | 5. сы |
/, см | <J>, градусы | р, см | с | Л, см | |
| 21 |
7.5 | 56.5 | 142. | 2.60 | 5150. | 0 0 | .100Е | 21 |
0.85 | 100 |
| 22 | 7.5 | 56.5 |
142, | 2.60 | 5150. |
0.0 | Л00Е | 21 | 0.85 | 100. |
| 23 | 7.5 | 56.5 | 142, | 2.60 |
3000. | 00 | Л00Е |
21 | 0.85 | 100. |
| 24 | 7.5 |
56.5 | 142, | 2.60 |
1000. | 00 | 100Е | 21 | 0.85 |
100. |
| 25 | 7.5 | 56.5 | 142. |
2.60 | 500. | —11.25 | 100Е | 21 | 0 85 | 100. |
| 26 | 7.5 | 56.5 |
142. | 2.60 | 58. |
—22.50 | .150Е | 03 | 0 85 | 100. |
| 27 | 7.5 | 56.5 | 142. | 2.60 |
58. | —22.50 | .150Е | 03 | 0.85 |
100. |
| 28 | 7.5 | 56.5 | 142. |
2.60 | 58. | —22.50 |
. 150Е | 03 | 0.85 | 100. |
| 29 |
7 5 | 56.5 | 142. | 2.60 | 59. |
—11.25 | 150Е | 03 |
0.85 | 100. |
|
30 | 7 5 | 56.5 |
142. | 2.60 | 500 | 0.0 | 100Е |
21 | 0.85 | 100 |
| 31 | 7 5 |
56.5 | 142. | 2.60 |
1350 | 0.0 | 100Е | 21 | 0.85 |
100 |
| 32 | 7 5 | 56.5 | 142. |
2.60 | 1350 | 0.0 |
100 Е | 21 | 0.85 | 100 |
| 33 |
7.5 | 56.5 | 142. |
2.60 | 500 | 11.25 | 100Е | 21 |
0.85 | 100 |
| 34 | 7.5 | 56.5 |
142. | 2 60 | 58. |
22 50 | Л БОЕ |
03 | 0.85 | 100 |
| 35 | 7.5 |
56,5 | 142, | 2.60 |
58. | 22 50 | . 150Е | 03 | 0.85 |
100. |
| 36 | 7.5 | 56 5 | 142, |
2.60 | 58. | 22.50 |
150Е | 03 | 0.85 | 100 |
| 37 |
7.5 | 56.5 | 142. |
2.60 | 59. | 11.25 | 150Е | 03 | 0 85 | 100. |
| 38 | 7.5 | 56.5 |
142. | 2.60 | 500. |
0.0 | 0.100Е | 21 | 0 85 | 100. |
| 39 | 7.5 | 56 5 | 142. | 2.60 |
1000 | 0.0 | 100Е |
21 | 0.85 | 100, |
| 40 | 7.5 |
56.5 | 142. | 2 60 |
1500. | 0.0 | 100Е | 21 | 0 85 |
100. |
| 41 | 7.5 | 56.5 | 142 |
2.60 | 3550 | 00 |
100Е | 21 | 0.85 | 100. |
| Номер участка |
а, см | Я". МПа |
PRG | 7гр, МПа |
^гр' градусы |
Сгр, МПа | ?гр, МПа | •*гр |
сх 0, МПа, см |
Ягр. МПа |
| 2 |
24 | 400 | Q |
19 | 35. | 001 | 30 | .25 |
.020 | 4 |
| 3 | 24, | 400 | 0 | 19 | 35. |
001 | 30 | .25 |
.020 | 4 |
|
4 | 24 |
400 | 0 |
19 | 35. | 001 | 30 | .25 |
.020 | 4 |
| 5 | 24. | 400 | 0 | 19 | 35. |
.001 | 30 | .25 |
.020 | .4 |
|
6 | 24. | 350 |
0 | 19 | 35. |
001 | 30 | .25 |
.020 | .4 |
|
Номер участка | а, см | Я1,,- МПа |
PRO | J^rp* ИПЛ |
Ф гр' градусы | еГр. МП» | ?гр> МПа |
**гр | сх 0> МПа с.м | Ягр. МПа |
| 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 | 24. 24. 24. 24. 24. 24. 24. 24. 24. 24. 24. 24. 24. 24. 24. 24. 24. 24. 24. 24. 24. 24. 24. 24. 24. 24. 24. 24. 24. 24. 24. |
350 350 350 400 400 400 400 350 350 350 350 400 400 400 400 400 400 400 400 350 350 3.50 350 400 400 400 400 350 350 350 350 | 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 | 19 19 19 19 19 19 19 19 19 19 19 19 19 19 19 19 19 19 19 19 19 19 19 19 19 19 19 19 19 19 19 |
35. 35. 35. 35. 35. 35. 35. 35. 35. 35. 35. 35. 35. 35. 35. 35. 35. 35. 35. 35. 35. 35. 35. 35. 35. 35. 35. 35. 35. 35. 35. | .001 .001 .001 .001 .001 .001 .001 .001 .001 .001 .001 .001 .001 .001 .001 .001 .001 .001 .001 .001 .001 .001 .001 .001 .001 .001 .001 .001 001 001 .001 | 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 | .25 .25 .25 .25 .25 .25 .25 .25 .25 .25 .25 .25 .25 .25 .25 .25 .25 .25 .25 25 .25 .25 .25 .25 .25 .25 .25 .25 .25 .25 .25 | .020 .020 020 .020 .020 .020 020 020 .020 .020 .020 .020 .020 .020 .020 .020 .020 .020 .020 .020 .020 .020 .020 .020 .020 .020 .020 .020 .020 .020 .020 | .4 .4 .4 .4 .4 .4 .4 .4 .4 .4 .4 .4 .4 .4 4 4 .4 4 .4 .4 .4 .4 .4 .4 .4 .4 4 .4 .4 .4 .4 |
¦
| Номер узла | Yyд. гр. кН.м» | к Н • м | |
|
1 2 | 28 | 11 | |
| 3 | 28 | 11 | |
| 4 | 28 | И | |
| 5 | 28 | 11 | |
| 6 | 28 | 11 | |
| 7 | 28 | 11 | |
| 8 | 28 | 11 | |
| 9 | 28 | 11 | |
| 10 | 28 | 11 | |
| 11 | 28 | 11 | |
| 12 | 28 | И | |
| 13 | 28 | 11 | |
| 14 | 28 | 11 | |
| 15 | 28 | и | |
| 16 | 28 | 11 | |
| 17 | 28 | 11 | |
| 18 | 28 | И |
П р о А о Л /к с- и » О
| Номер участка |
а. см | МПа |
PRG | тур» МПЗ |
•Frp’ градусы |
сгр. МПа | ?гр. МПа | ^гр |
сх 0. МПасм |
Дгр. МПа |
| 38 39 40 41 | 24. 24. 24. 24. | 400 400 400 400 | 0 1 1 1 |
19 16 16 16 | 35. 22. 22. 22. | .001 .028 .028 .028 | 30 19 19 19 | .25 .40 .40 .40 | .020 .030 .030 .030 | .4 .2 .2 .2 |
| Узлопыс усилия | ||||||
| е |
Ав, см | ^груза’ Н:с« | 9а нк’ н см | Z,. н « | г .л н | Zy н |
|
0.75 0 75 0.75 0.75 0 75 0 75 0.75 0.75 0.75 0.75 0.75 0.75 0.75 6.75 0.75 0.75 0.75 | 20. 20. 20. 20. 20 20. 20. 20. 20. 150. 150. 150. 150. 150. 150. 150. 150. | 140 140 140 140 140 140 140 140 140 120 120 120 120 120 120 120 120 | 00 00 00 0.0 0.0 0.0 0.0 0.0 00 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 | 0.0 0.0 00 0 0 0.0 00 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 |
00 2.0 0 0 0 0 00 00 0 0 о.о о.о 0 0 о.о о.о 00 о.о о.о о.о о.о о.о | 0.0 0.0 00 0 0 0.0 0.0 0.0 0.0 00 00 0.0 0.0 0.0 0.0 0.0 0,0 0.0 0.0 |
•c ^ •с ГС
к о
— О©.— 00~«00>—ОО — О О — О О ¦— О О — О О — О О >— ОО
ослоосло о сл oobibboiooyiobbibo'cnoboioboib
ooooooooooolIII
bic^’oobobpiDiDoobobo^ со Lo сл •** >-s] CD Ю Ю О — — о> — — to © о оэ со to^-Js.^4kCr>Ot40Q500Ot0tO^00 »— 001000СЛ^С00^4 — *-4^3(000
mmmmrnmmmmmmmrTimm
OOOOOOOOOOOOOOOOOOOOO
-jNOia)0)05^oo505oo5ffl O)Gi0O5C7)O5O5O)
о о oo
• to кэ со bi ооссч
СО >— i— СО
— со *— СЛ ЙИИИ
ю — ^ '•q СО“Ц
СО tO -4
1—¦ to
спгпгп
^юю ОС О “-J
оо — со
00 со — тгпсп
О 03 *ч| — -4 03
мига
-vi —
CO *—
— сл
mm
з:?
ООО
Сл Сл 4^
ООО
ООО
О О сл
ОООООООООООООООООООООООООООООО
Релуль гиты ^расчет а
ОССОСО О
К) ю ос о
_ _ _ Ol сл to ^
nmmmrcrarornrammtflmmmmmrampimraram
0О *->J “>1 ¦4 01 —
СО 05 сг> —
tnmm
со to rw
О ООО -о со SfDO
mmtrj
OOOOOOOOOOOOOQOOOOOOCO
со^слоз^^^--ооооооо^^лю оо—осО — Ооо-^сл^сосогоослсоооо
ОООООООООООООООООООО
OoOoOCQCOCOCCdOoQCOOOCQCOCCOOOOO^J“-J-4-4|
О о о о
*4 -4
ООО
-vl -vl ~vj
ООО
•-J Оо
оо | ‘ J J J J J J J I oooooooo I I . _ _
io — — Ьэ is» — — — — — — coto‘—* — ooicoco”— — — bi
-40СООЗ~-ЮОСЮ-4срСООО*ОСЛ<ОСО-4**г*'^ — ГОЮ — О О СО СО СО <T> СИ СЛОЮЮСООСООООСЛ — Ooc-J^fOOOCOCOCOCOOT*— >— го сл сл со
со со о — — -^союсо-^осло — ^Oocoai-J — — cototoo^^-^to tnmtommmmcncnrnrnrncnrntfltnrnrnrntncncnrrjmrntntntnrntn
ОООООООООООООООООООООООООООООО
ОООЭООО-ОООСЪОООООООООООО^СЛСЛСЛСЛСЛ^СО
о о
ООООООООООООООООООООООООО I
• — ОС *-4
f оо
-4 — —
СЛ 00 »0 О “-30 ОС CD О
mrnm
*° я 2S
g-s
п> <2
ЬЭЮСО^СЛСЛСЛСПСЛСЛ^^^ЮЬЭЬО- — — — >?* —
ОО--4С0О — СО*—ЮЮС0С0.?*0000-400^ОО00 — 0000 — СЛСЛООО^- — ОЮоо — О © Q0 — 000^400
ЮСОО^Ю.Ь'СЛ^СЛ^СОСЛСЛСЛСЛСОСО^СОСО — СЛ
сп m m сп гг» tn tv т яиии п? и ггзш гягя пз га пз гч оооооооооооооооооооооо
>t- о — со оо со
-р- -v|
меч
СО
00
гпгпеп
,±
28
о о ос о — — •¦
^ОООООООООООООООООООО
-Z— — ^coW^^^LT^^^.^COCOCONDtO — ^ n^^COCOCO^-'j*^ — 0--q^J030CD03-vJ-^|COCr> _-oooO“'4aitoa>4i. — ^ооослсло«ооооосг>ю ОС0СЛ-а)03С0^С0ЮОУ1(ОЮ^С0Ча)СЛ01ОЩ
rnrnmmmrrimmmmmmmnimrnmrnrTiwrnrn
ОООООООООООООООООООООО
15
и
(О
- э*
X 3 О Q
" л>
Сл ^ — *Т* Сл Сл
ооо
О *vi -^1
— со со гпгпгп
) to js*
] GO О
3 to to i m гп
СЛ о
~-4 СО
гп гп
5 О О С
^^WCOWUCOWWWWCtflOWMtOMKjMMtoW'-
^O{DQO4OJ^4»WK3'-O0OOSfl5Oi^WK)'-O(D
X'<
213
ICK)WbOJOMb3MtOlOWMtOU)tOtOtOtOtOMNOWtO ОООООООООООЭООООООФССООООО OOOOOOOOOOOOOOODOC
oooooooooooooo о
СЛ ' *
I oooooooo
СЛ СЛ СЛ СЛ СЛ СЛ СЛ СД Oi СЛ СЛ Сд СЛ СЛСЛСЛСЛСЛСЛСЛСЛСЛ
wucowwwwwco
ООООООООО
ооооооооо
ООООООООО ООО
to ю to to to to — — ь— ООООООСЛСЛСЛ ООООООООО
о о
OOOOOOOOOOOOOO оООООО*— — *— OOOOOOOOOOOOOO ООООООООО
о I— — ооо
ООООООООфО
ОООООООООО
ООООООООООООООООООООООО
ООООООООООООООООООООООО
oooooooooooooo ооооооооо
ООООООООООООООООООООООО
Ха
п*<
3S«
ООООООООО
о О о о
О о о о о о
N
X
N
X
о
OOOOOOOOOOOOOO
OOOOOOOOOOOOOO
ООООООООО
ооооооооо
| Координаты |
Изгибающий момент, Н'М |
Продольное усилие. Н |
|
0.0 | 0.1617Е Об | 0.9677Е 07 |
| 0 5 | 0 1741Е 07 | 0.9787Е 07 |
|
1.0 | 0.2075Е 07 | 0 1018Е 08 |
| 0.0 | 0.2073Е 07 | 0.1018Е 08 |
|
0.5 | 0.1353Е 07 | 0.1033Е 08 |
| 1.0 | —.1823Е 06 | 0.1051 Е 08 |
|
0.0 | —.1809Е 06 | 0.1036Е 08 |
| 0.5 | — 3905Е 06 | 0.1037Е 08 |
| 1 0 | —-6150Е 06 | 0.1038Е 08 |
| 0.0 | — 6138Е 06 | 0 1012Е 08 |
| О 5 | — 7643Е 06 | 0.1010Е 08 |
| 1.0 | —.9301Е 06 |
0.1008Е 08 |
| 0 0 |
—.9293Е 06 | 0.9928Е 07 |
| 0.5 | —.9914Е 06 |
0 9909Е 07 |
| 1 0 |
— 1065Е 07 | 0.9889Е 07 |
| 0 0 | — .1065Е 07 |
0.9870 Е 07 |
| ОБ |
—.1017Е 07 | 0.9850Е 07 |
| 1 0 | — 9760Е 06 |
0.9830Е 07 |
| 0 0 |
— 9786Е 06 | 0.9878Е 07 |
| 0 5 | — 2466Е 06 |
0.9709Е 07 |
| 1.0 |
0.2895Е 06 | 0.9546Е 07 |
| 0 0 | 0 2093Е 06 | 0 9546Е 07 |
| 0.5 |
0.5481 Е 05 | 0.9201 Е 07 |
| 1 0 | 0 4814Е 06 | 0 8881Е 07 |
| 0 0 | 0 4814Е 06 | 0 8881Е 07 |
|
0.5 | 0.3393Е 05 | 0.7745Е 07 |
| 1 0 | — .I999E 05 | 0.6893Е 07 |
|
0.0 | — 1999Е 05 | 0.6893Е 07 |
| 0.5 | 0 1029Е 04 | 0 4136Е 07 |
|
10 | 0.2196Е 01 | 0.3558Е 07 |
¦
| Попереч ивя сила, Н | Поперечное перемещение, см |
Продольное перемещение, см | |||
| 0.2753Е | 06 |
0.4185Е | -01 | — 5474Е- | -01 |
|
0.1992Е | 06 | —.9612Е | 00 | 0 4499Е |
00 |
| —.1582Е |
06 | — .3069Е | 01 |
0 9611Е | 00 |
|
— .1582Е | 06 | — .3069Е | 01 | 0.9611Е |
00 |
| — .4350Е |
06 | —.4303Е | 01 | 0 1168Е | 01 |
| — .8109Е | 06 |
—.5676Е | 01 | 0 1378Е | 01 |
| —.6967Е |
06 | —.5830Е | 01 | 0.2443Е | 00 |
| —.7484Е | 06 |
—.5987Е | 01 | 0.2685Е | 00 |
| —.8014Е |
06 | — .6131Е |
01 | 0.2927Е | 00 |
| ~4941Е | 06 |
—.5770Е | 01 | —.2075Е | 01 |
| —.5452Е | 06 | — .5896Е |
01 | -.2051Е | 01 |
| —.5973Е | 06 |
—.5999Е | 01 |
—.2027Е | 01 |
|
-.1923Е | 06 | —.4764Е | 01 | -.4160Е |
01 |
| —.2343Е |
06 | —.4839Е | 01 |
— 4145Е | 01 |
|
—.2769Е | 06 | — 4885Е | 01 | — 4121Е |
01 |
| 0.1783Е |
06 | —.2935Е | 01 |
—.5677Е | 01 |
| 0.1521 Е | 06 | — 294 5Е | 01 | -5652Е |
01 |
| 0.1259Е |
06 | — .2931Е | 01 |
— .5628Е | 01 |
| 0 35Е2Е | 06 |
—.1781Е | 01 | —.6096Е | 01 |
| 0.2333Е |
06 | — .1465Е | 01 | —.5983Е | 01 |
| 0.1359Е | 06 | — .1120Е | 01 | —.3692Е | 01 |
| 0.1359Е |
06 | — 1120Е | 01 | —.5692Е | 01 |
| 0.1472Е | 05 |
—.5182Е | 00 | —.5295Е | 01 |
| —.3186Е | 05 | — 1381Е |
00 | —.4905Е | 01 |
| —3186Е | 05 |
—. 1381Е | 00 | — .4906Е | 01 |
|
—-14JOE | 05 | О 7415Е | 01 | —.3783Е |
01 |
| 0.1468Е |
04 | 0.4713Е— | -02 | —.2724Е | 01 |
| 0.1468Е | 04 |
О 4713Е—02 | —.2724Е |
01 | |
| —.1756Е |
02 | —.6446Е- | 03 |
—.Ш7Е | 01 |
|
— .8289Е | 01 | — .5532Е- | 05 | 0.3117Е |
00 |
Продольное перемещение, ем
Поперечная сила, Н
Продольное усилие, И
00
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
00
00
00
01
01
01
01
00
0.3J17E 0.1768Е 0 3406Е 0.3406Е 0 4469Е 0.5591Е 0.5592Е 0.5980Е 0.6375Е 0.6375Е 0.6575Е 0.6777Е 0.6272Е 0.6295Е 0.6319Е 0.4612Е 0.4636Е 0 4660Е 0.2298Е 0.2322Е 0.2346Е —.2707Е
— 2462Е —.2216Е —.1472Е —.1263Е —.I056E
- 1056Е —.5058Е
0.3558Е 0 4532Е 0.6954Е 0.6954Е 0.7779Е 0.8833Е О.&ЙЗЕ 0.9133Е 0.9453Е 0.9453Е 0.9606Е 0.9763Е 0.9711Е 0.9729Е 0 9747Е 0.9770Е 0.9788Е 0.9806Е 0.9982Е 0.1000Е 0.1001Е 0.1030Е 0 ЮЗОЕ 0.Ю29Е 0 1046Е 0.1029Е 0.1015Е 0.1015Е 0.9688Е 0.9546Е
—.8289Е —.I580E 0 1 549Е 0.1549Е
— .1544Е
— .3345Е —.3345Е
0.1824Е 0.1508Е 0.1508Е 0.2568Е 0.3898Е 0.1364Е 0.1646Е 0.1927Е —.3106Е
— .2637Е —.2175Е —,6671Е
— .6097Е
— 5534Е
— .8962Е
— 8366Е
— .7785Е —.9054 Е
— .4921Е -.1911Е —.1911Е
0.1959Е
0.2463Е
01
02
04
04
05 05 05
05
06 06 06 06 06 06 06 06 06 06 06 06 06 06 06 06 06 06 06 06 06 06
07
07
07
07
07
07
07
07
07
07
07
07
07
07
07
07
07
07
07
08 08 08 08 08 08 08 08 08 07 07
00
00
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
01
00
00
Координаты
| 0.0 | 0.2196Е 01 |
| 0.5 | —-1104Е 04 |
| 1 0 | 0 2164Е 05 |
| 0.0 | 0 2164Е 05 |
| 0.5 | —.3853Е 05 |
| 1.0 | —.5204Е 06 |
| 0.0 | — 5204 Е 06 |
| 0.5 | — .5844 Е 06 |
| 1 0 | — 2028Е 06 |
| 0.0 | — 2028Е 06 |
| 0,5 | 0 3009Е Об |
| 1 0 | 0 1104Е 07 |
| 0.0 | 0 1100Е 07 |
| 0.5 | 0 1144Е 07 |
| 1.0 | 0 1196Е 07 |
| 0.0 | 0 1196Е 07 |
| 0.5 | О.ШЗЕ 07 |
| 1 0 | 0 1043Е 07 |
| 0.0 | 0.1043Е 07 |
| 0.5 | 0 8590 Е 06 |
| 1 0 | 0 6902Е 06 |
| 0.0 | 0.6921 Е 06 |
| 0 5 | 0 4368Е 06 |
| 1.0 | 0 1983Е 06 |
| 0 0 | 0 1995Е 06 |
| 0.5 | — 1523Е 07 |
| 1 0 | —.2355Е 07 |
| 0 0 | —.2355Е 05 |
| 0.5 | —.2053Е 07 |
| 1 0 | —.4526Е 06 |
Изгибающий момент. Н м
—.5532Е—05 0.7149Е—03 —.8380Е—02 —.5380Е—02 —.8020Е—01 0.1563Е 00 0.1563Е 0.5705Е 0.1220Е 0.1220Е 0.1590Е 0.1924Е 0.3206Е 0.3221 Е 0.3203Е 0.5377Е 0.5322Е 0.5235Е 0.6623Е 0.6505Е 0.6361 Е 0.6779Е 0.6610Е 0.6429Е 0.6265Е 0 4709Е 0.3310Е 0.3310Е Q.8133E — .1509Е
Поперечное перемещение. см
Изгибающий момент. Н м
Продольное усилие. Н
Поперечная сила, Hj
Продольное перемещение, ем
| — .4526Е | 06 | 0.9546Е |
07 | 0.2463Е | 06 |
| 0 9818Е | 06 |
0.9731Е | 07 | 0.1590Е | 06 |
| 0.1303 |
07 | 0.1024Е | 08 | —. 1077Е | 06 |
| 0.1303Е | 07 |
0.1024Е | 08 | — .1077Е | 06 |
| 0 8J89E |
06 | 0.1040Е |
08 | —.2891Е | 06 |
| — .1918Е | 06 |
0.1059Е | 08 |
—.5299Е | 06 |
|
—.1509Е | 06 | 0.1049Е | 08 | — .4361Е |
06 |
| -.3221Е |
06 | 0.1051Е | 08 |
— .4701Е | 06 |
|
—.4636Е | 06 | 0 1053Е | 08 | —.504 8Е |
06 |
| —.4627Е |
06 | 0 1038Е | 08 |
—.2809Е | Об |
| — .5494Е | 06 |
0.1036Е | 08 | —.3165Е | 06 |
| — .6462Е | 06 | 0.1034Е |
08 | —.3526Е | 06 |
| —,6459Е | 06 |
0.Ю26Е | 08 |
—.6635Е | 05 |
|
—.6699Е | 06 | 0.1024Е | 08 | —.9776Е |
05 |
| — .7027Е |
07 | 0.1022Е | 08 |
—.1293Е | 06 |
|
—,7031В | 06 |
0.1023Е | 08 | 0.1872Е | 06 |
| — .6516Е | 06 | 0.1021Е |
08 | 0.1649Е | 06 |
| — .6958Е | 06 |
0.1019Е | 08 |
0.2428Е | 06 |
|
—.6073Е | 06 | 0.1023Е | 08 | 0.3021Е |
06 |
| —.8670Е |
04 | 0 100 5Е | 08 |
0.1811Е | 06 |
|
0.3204Е | 06 |
0.9887Е | 07 |
0.8653Е | 05 |
|
0.3204Е | 06 | 0.9887Е | 07 | 0.8653Е |
05 |
| 0.5205Е |
06 | 0 9337Е | 07 |
0.3813Е | 04 |
|
0.Ф428Е | 06 | 0.8856Е | 07 | —.2839Е |
05 |
| 0.4428Е |
06 | 0 8856Е | 07 |
—.2839Е | 05 |
|
0.2069Е | 06 | 0 7974Е | 07 | — 288GE |
05 |
| 0 4542Е |
05 | 0.7306Е | 07 |
— .1403Е | 05 |
|
0 4542Е | 05 | 0.7306Е | 07 | — .1403Е |
05 |
| —1849Е |
05 | 0.5249Е | 07 |
0Л307Е | 04 |
|
0 1286Е | 04 | 0.5849Е | 07 | 0.5923Е |
03 |
| —Л509Е | 00 |
0.3583Е—01 | |
| — .74 78Е |
00 | 0.5781 Е | 00 |
| —.204 5Е | 01 | 0.1130Е | 01 |
| —.2045Е | 01 |
0.U30E | 01 |
|
—.2785Е | 01 | 0.1338Е | 01 |
| — .3608Е | 01 | 0 1548Е |
01 |
| —.3836Е |
01 | 0.8150Е |
00 |
| —.3929Е |
01 | 0.8394Е | 00 |
| — .40Г2Е | 01 |
0.8638Е | 00 |
|
—.4032Е | 01 | —.7368Е | 00 |
| — -4100Е | 01 | —.7126Е |
00 |
| —.4153Е |
01 | —.6884Е | 00 |
| —.3571Е | 01 |
—.2225Е | 01 |
|
-.3604Е | 01 | -.2201Е | 01 |
| —.36J7E |
01 | — 2I77E | 01 |
| —.2509Е | 01 |
— 3396Е | 01 |
| — .2498Е | 01 | — .3371Е | 01 |
|
—.2472Е | 01 | — .3347Е | 01 |
| — .1774Е | 01 | —.3767Е |
01 |
| —.1429Е |
01 | —.3560Е | 01 |
| —. 10 82 Е | 01 |
— .3356Е | 01 |
|
—. 10 82Е | 01 | — 3356Е | 01 |
|
-.5026Е | 00 | -2954 Е | 01 |
| — .1372Е | 00 | —.2563Е |
01 |
| — Л372Е |
00 | —.2563Е | 01 |
| 0.7899Е— | -01 |
—.1999Е | 01 |
|
0 8790Е- | -01 | -.1459Е | 01 |
| 0.8790Е- |
-01 | —.1459Е | 01 |
| 0 4760Е— | -02 | —-2977Е | 00 |
| — 23Q6E- | -02 |
0.8104Е | 00 |
0.0 0.5 /.О 0 0 0.5 1.0 0.0 0.5
3.0 0.0 0.5
1.0 0.0 0.5 1.0 0.0 0.5 1.0 0.0 0.5 1.0 0.0 0.5 1.0 0.0 0.5 1 о 00 0.5 1 0
Прочностной расчет
МПа
1Я1ф *1'
°пр 2’ МПа
МПа
°ир г' МПа
Нм
М
пр II
деф’
Координаты
| —.4809Е | 04 | 0 630Е | 02 |
| 0.1337Е | 05 |
0-667Е | 02 |
|
—.2744 Е | 05 | 0 779Е | 02 |
| -.2744Е |
05 | 0 779Е | 02 |
| -.2021Е | 06 |
0.849Е | (12 |
| —.4905Е | 06 |
0.953Е | 02 |
| — .4903Е | 06 | 0.953Е |
02 |
| — .5890Е |
06 | 0.996Е | 02 |
| — .3035Е | 06 |
0 942Е | 02 |
|
—.3034Е | 06 | 0.942Е | 02 |
| 0 1204Е |
06 | 0.904Е | 02 |
| 0.8206Е | 06 |
0.109Е | 03 |
|
0 8179Е | 06 | 0.189Е | 03 |
| 0.8648Е |
06 | 0.195Е | 03 |
| 0.9185Е | 06 |
0.202Е | 03 |
|
0 9186Е | 06 | 0 202Е | 03 |
| 0.8668Е |
06 | 0.195Е | 03 |
| 0 8261Е | 06 |
0.190Е | 03 |
|
0.8265Е | 06 | 0 191Е | 03 |
| 0.6932Е |
06 | 0.175Е | 03 |
| 0.5732Е | 06 |
0.160Е | 03 |
|
0.5744Е | 06 | 0.162Е | 03 |
| 0.3817Е |
06 | 0.138Е | 03 |
| 0.2022Е | 06 |
0.116Е | 03 |
|
0.2034Е | 06 | 0.975Е | 02 |
| —.1J17E |
07 | 0.I20E | 03 |
| —Л734Е | 07 |
0.135Е | 03 |
|
— .1734Е | 07 | 0.135Е | 03 |
| — .I383E |
07 | 0.I2IE | 03 |
| 0.1622Е | 06 |
0.891Е | 02 |
0.323Е
0.323Е
0.323Е
0.332Е
0.323Е
0.323Е
0.323Е
0.323Е
0.323Е
0.323 Е
0.323Е
0.323Е
0.906Е
0.906Е
0.906Е
0.906Е
0.906Е
0.906В
0.906Е
0.283Е
0.283Е
0.283Е
0.283Е
0.283Е
0.323Е
0.323Е
0.323Е
0.323Е
0.323Е
0.323Е
03
03
03
03
03
03
03
03
03
03
03
03
02
02
02
02
02
02
02
03
03
03
03
03
03
03
03
03
03
03
0.627Е 0.660Е 0.7G5E 0.765Е 0.745Е 0.701Е 0.701 Е 0.694Е 0.786Е 0.736Е 0.842Е 0.672Е —.136Е —.193Е —.258Е —.259Е —.193Е —.142Е — .132Е 0.344Е 0.184Е 0.201Е 0.439Е 0 661Е 0.871 Е 0.626Е 0.459Е 0.459Е 0.510Е 0.808Е
02
02
02
02
02
02
02
02
02
02
02
02
02
02
02
02
02
02
02
01
02
02
02
02
02
02
03
02
02
02
0.323Е
0.323Е
0.323Е
0.323Е
0.323Е
0.323Е
0.323Е
0.323Е
0.323Е
0.323Е
0.323Е
0.323Е
0.283Е
0.283Е
0.283Е
0.283Е
0.283Е
0.283Е
0.283Е
0.283Е
0.283Е
0.283Е
0.283Е
0.283Е
0.323Е
0.323Е
0 323Е
0.323Е
0.323Е
0.323Е
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
0.0 0.5 1.0 00 0.5 1.0 0.0 0.5 1.0 0.0 0.5 1.0 0.0 0.5 1 0 0.0 0.5 ] 0 0.0 0.5 J.0 0.0 0.5 1.0 0.0 0.5 1 0 0.0 0.5 1.0
g
СП
Номер
участка
м
деф’
Н м
стпр 1' МПа
|
0.1622Е | 06 | 0 891Е | 02 |
| 0.1746Е |
07 | 0Л30Е | 03 |
| 0.2080Е | 07 |
0.142Е | 03 |
|
0.2080Е | 07 | 0.142Е | 03 |
| 0.1355Е |
07 | 0.125Е | 03 |
| —Л825Е |
ОС | 0.970Е | 02 |
| —.1812Е | 06 |
0.113Е | 03 |
|
—.3921Е | 06 | 0.139Е | 03 |
| — 6160Е |
06 | 0 167Е | 03 |
| — 6151Е | 06 |
0.165Е | 03 |
|
— .7661Е | 06 | 0.183Е | 03 |
| —-9321Е |
06 | 0.204 Е | 03 |
| — 9316Е | 06 |
0.202Е | 03 |
|
— .9939Е | 06 | 0.210Е | 03 |
| — .10G8E |
07 | 0.219Е | 03 |
| — .1068Е | 07 | 0.219Е | 03 |
| —.1020Е | 07 |
0.213Е | 03 |
|
—.9786Е | 06 | 0.207Е | 03 |
| -.9811Е |
06 | О.ШЕ | 03 |
| —.2473Е | 06 |
0.916Е | 02 |
|
0.2102Е | 06 | 0.892Е | 02 |
| 0.2102Е |
06 | 0.892Е | 02 |
| 0.5502Е | 06 |
0.949Е | 02 |
|
0 4835Е | 00 | 0 904 Е | 02 |
| 0.4835Е |
06 | 0.904Е | 02 |
| 0 3415Е | 05 |
0 688Е | 02 |
|
- .2016Е | 05 | 0.610Е | 02 |
| — .2016Е | 05 | 0.610Е |
02 |
| 0.1043Е |
04 | 0 363Е | 02 |
| 0.2228Е | 01 |
0 312Е | 02 |
Координаты
t^np ll’
МПа
% «Па
[°пр *]• МПа
12
12
12
13
13
13
14 14
14
15 15
15
16 16 16 17 17
17
18 18 18 19 19
19
20 20 20 21 21 21
0.0
0.5
1.0
0.0
0.5
1.0
0.0
0.5
1.0
0.0
0.5
1.0
0.0
0.5
1.0
0.0
0.5
1.0
0.0
0.5
1.0
0.0
0.5
1.0
0.0
0.5
1.0
0.0
0.5
1.0
0.323Е
0.323Е
0.323Е
0.323Е
0.323Е
0.323Е
0.283Е
0.283Е
0.283Е
0.283Е
0.283Е
0.283Е
0.283Е
0.283Е
0.2S3E
0.283Е
0.283Е
0.283Е
0.323Е
0.323Е
0.323Е
0.323Е
0.323Е
0.323Е
0.323Е
0.323Е
0.323Е
0.323Е
0.323Е
0.323Е
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
0.808Е 0.411Е О 360 Е 0.360Е 0.559Е 0.876Е 0 685Е 0.425Е 0.147Е 0 125Е
— .634 Е
— .271Е —.284Е —.363 Е
— .457Е
— .459Е —.401Е —.35IE
0.615Е 0.789Е 0.784Е 0.784Е 0.666Е 0.655Е 0.655Е О,671Е
о.еооЕ
0.600Е
О.ЗбЗЕ
0.312Е
02
02
02
02
02
02
02
02
02
02
01
02
02
02
02
02
02
02
02
02
02
02
02
02
02
02
02
02
02
02
0.323Е
0.323Е
0.323Е
0.323Е
0.323Е
0.323Е
0.283Е
0.283Е
0.283Е
0.283Е
0.906Е
0.906Е
0.906Е
0.906Е
0.906Е
0.906Е
0.906Е
0.906Е
0.323Е
0.323Е
0.323Е
0.323Е
0.323Е
0.323Е
0.323Е
0.323Е
0.323Е
0.323Е
0.323Е
0.323Е
03
03
03
03
03
03
03
03
03
03
02
02
02
02
02
02
02
02
03
03
03
03
03
03
03
03
03
03
03
03
Продолжение
[«Val- МПа
<Г„р s. МПа
Гпрг!' Л1Па
Номер
участка
Л,деф' Н м
Координаты
0.323Е
0.323Е
0.323Е
0.323Е
0.323Е
0.323Е
0.323Е
0.323Е
0.323Е
0.323Е
0.323Е
0.323Е
0.906Е
0.906Е
О 906Е
О 906Е
О 906Е
0.906Е
0.906Е
0.906Е
0.283Е
0.283Е
0.283Е
0.283Е
0.323Е
О 323 Е
0.323Е
0.323Е
0.323Е
0.323Е
03
03
03
03
03
03
03
03
03
03
03
03
02
02
02
02
02
02
02
02
02
03
03
03
03
03
03
03
03
03
02
02
02
02
03
02
02
02
02
02
02
02
02
02
02
02
02
02
02
02
01
01
02
02
02
02
02
02
02
02
0.312Е 0.397Е 0.605Е 0.605Е 0.673Е 0.641Е 0.641Е О 651Е 0.778Е 0.778Е О 766Е 0.573Е
— ,516Е
— 569Е —.632Е —.630Е —.525Е —.436Е —.421Е —.190Е
0.212Е 0.447Е 0.361 Е 0.657Е 0.8676 0.512Е 0.286Е 0.286Е 0.322Е 0.721Е
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
03
0.323Е
0.323Е
0.323Е
О 323Е
0.323Е
0.323Е
О 323Е
0.323Е
0.323Е
0.323Е
О 323Е
О 323Е
О 283Е
0.283Е
0.283Е
0.283Е
0.283Е
0.283Е
0.283Е
0.283Е
О 283Е
О 283Е
0.283Е
0.283Е
0.323Е
0.323Е
0.323Е
О 323Е
0.323Е
О 323Е
0.312Е О 398Е 0.616Е 0.616Е О 693Е 0.909Е 0.909Е 0.952Е 0.882Е 0.882Е 0.921Е 0.114Е О 222Е 0.227Е О 234 Е 0 234Е 0.224Е 0.215Е О 217Е 0.194Е 0.173Е О 176Е 0.144Е О 115Е 0.969Е 0.129Е 0.149Е О 149Е О 137Е О 954Е
02
02
02
02
02
02
02
02
02
02
02
03
03
03
03
03
03
03
03
03
03
03
03
03
02
03
03
03
03
02
0.2228Е
— .11 (8Е 0.2181Е 0.2181Е
—.3880Е
— .5228Е —.5228Е
— .5868Е
— .2034Е
— 2034Е 0.3019Е 0 1107Е 0.1 ЮЗЕ 0.1147Е 0 1199Е 0.1199Е О.П16Е 0.1045Е 0.1046Е 0.86ЮЕ 0 691Е 0.6933Е 0 4376Е О 1986Е 0.1998Е
—.1525Е —.2359Е —.2359Е —.2059Е
— .4540Е
01
04
05 05
05
06 06 06 06 06 06 07 07 07 07 07 07 07 07 06 00 06 06 06 06 07 07 07 07 06
0.0
0.5
1.0
0.0
0.5
1.0
0.0
0.5
1.0
0.0
0.5
1.0
0.0
0.5
1.0
0.0
0.5
1.0
0 о
0.5
1 0 00 0.5 1 0 00 0.5 1.0 0.0 0.5 1 0
22
22
22
23
23
23
24 24
24
25 25
25
26 26 26 27 27
27
28 28 28 29 29
29
30 30
30
31 31 31
Продолжение
сосососососососососососососо
оооооооооооооо
шшазшйшишшщышщси
СОСОСОСОСОСОСОСОСОСОСОСОСОСО
C^CMCMCMCMCMOOOOCOOOGOOOOOGO
СОСОСОСОСОСОС^С^СЧСЧСЧСЧСЧСЧ
со со со ООО
СО СО со СО СО СО
о о о о о о
СО СО СО СО СО СС СО
о о о о о о о
С
?
ы ш ш ил ш и: ш
SCO СО ГО СО СО СО ОС 00 00 СМ СЧ СЧ СЧ СЧ СЧ СЧ СО СО СО
шизшш из щц иш
СО СО СО С----
СЧ СЧ СЧ <
СО СО со с
- - - * См см см см з со со со со СО со
оооооооооооооооооооооооооооооо
| см |
сч | см | см | см | см см |
см | см | см |
см | см |
— | __ |
см | см | см |
сч | см | см | сч | см |
см | см | см |
сч см | ||
| о |
о | о | о |
о | оо | о |
о | о | о |
о | о | о |
о о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | оо |
|
U3 | и> | U3 |
ш | из | ЙЫ | и | W | из | U3 | U3 |
из | Ы | шш |
ш | и | ш |
ш | ш | ш |
из | из | ш | и | U3 | и | шш |
| — |
¦—* | тг |
СО | —« тГ | СО | СТ) | О |
г- | ю | .—. |
СТ) ^ | г- |
сч | ._, |
LO | ю | to |
СО | со | СО |
о | ст> | О со | |||
| сч | Q | со | о | о | 00 00 | сч | СО | см | о | оо | со | СО ^ | CD |
00 | оо | со |
00 | О | •sD | Ч* | сч |
см | LO — | |||
|
t"- | ср | LO |
Ю | Г-- | 00 о | lO | СО |
со | сч |
о | со | см см | 00 | Г-; | со | г- |
г- | о | so |
^о | со | CD |
CD | т}< Ю | ||
|
о | О | о |
о | о | о о |
о | о | о |
о | о | о |
о | оо | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о о |
а
с
с
| го |
со со | со |
со | со | со |
СО СО со | со |
со | со | со |
со | со | со | СО | со |
СО | со | со |
СО | со | СО | со | со |
со | со | со |
со |
| с |
о о | о | о |
о | о | ООО | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о |
| из из |
03 | U3 | W |
из | ШШ со | ш |
из | из | из | из | из |
из | из | ш |
ы | ш | ш |
из | ш | из | из | из |
из | из | ш |
ы | |
| *Н |
СО СО | со | со | СО | со | СО СО со | со | со |
со | со | со | со | со |
со | со | СО |
со | со | СО | со | со |
со | со | со |
со | со | со |
| сх | сч см | сч | см |
см | см | СО 00 со | оо | со |
оо | 00 | 00 |
00 | 00 | СО |
00 | см | см | см | см |
сч | сч | см |
см | сч | см | сч | см |
| со со | со |
см | со | со |
сч сч см | см |
см | сч | сч |
см | см | сч | см | см |
СО | СО | со | СО | со |
СО | со | со |
со | со | со | со | |
| сГ |
о о | о | о | о | о |
ООО | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о |
Выводы Конструкция удовлетворяет условиям по деформациям.
С\СОСОСОСОСЧСОСОСОСОСОСОСОСОСОСОСОСОСОСЧСЧСЧСЧСЧСЧСЧС'1СЧС'1СЧ
оооооооооооооооооооооооооооооо
^O^OCOCM05iOCMOOOO>«—ОСО^Г-О^ЮЮОО^СМСМСОСОСОЬОТ»* l0^{NCM-^r-'-'C0uj^i0Kr,NNNN'sDO:®,0ujiO0,)O)iOiDL'3tD^ CD — СЛ —* ~ч —«г— —¦ —.—«»-.,-*».-*аОСЛОСТ>аООСГ'-ОсОч34Ю
ОООООООООООООООООООООООООООООО
О CD о о
шы
С4 ю
S3
| сО | о | CD | CD |
СО | |
| о | о | о | о | о | о |
| из |
из | из | ш | ш | из |
| со | см |
см | о | iO | |
| о LO | г- TJ« | t"- 3 |
г— | о | о |
| ю | to |
'¦о | г- |
CD О
о о
ШИ со о
СМ I4-
in о
CD CD
СО СО Г- Г*- СО СС JD О ОООООООО
СО О CD о to о оо о о
О чЗ4 CD ООО
OJWWWCUCUCUtiJ о r-D LO IO СЯ - -гГ тГ О О О СЧ —• со lD СО СО СО CM CD СГ) СЧ rfCO — —'00~* — с0
цшш
tCS СТ) СЧ
со ОО —
ЦЩШШШШЩШИ
тГГ^СМСМ^СОСОтГСМ
^ ю ю с» со ад n о СМСМт»<тГ01ЛкОООСО СОЮт^т^СЧт**^—
-9-
о
оо о о
I I
ОООООООО
ОЮООЮООЮООЙСЗО^ООЮООЬОООЬОООЮООЮО ОО—-ОО — ОО'-ОО'^-ОО'—00 — 00 — ОО—'ОО — ОО'—
смсмсчсососо^^-^юю1псо,х>сог--г^г-сосоаоо>о>о>ооо—> — —
СОСОСОСОСОСОСОСОСОСОСОСОСОСОСО.СОСОСОСОСОСОСОСОСОТГ^Т^^-^Т^
is 55 ?
БАЛОЧНЫЕ СИСТЕМЫ НАДЗЕМНЫХ ПЕРЕХОДОВ С КОМПЕНСАТОРАМИ
Рассмотрим надземные переходи со специальными компенсаторами — Г /.Пи трапецеидальной конфигурации. Расчет таких систем можно разделить на два этапа. Прн малом числе пролетов вначале определяют Допускаемые расстояния между опорами, а затем параметры компенсаторов. При большом числе пролетов, когда устраивают несколько комненсаторов, чначале при принятых параметрах компенсатора определяют необходимое расстояние между ними, а затем расстояние между опорами.
Прн расчете крайних комненсаторов надземной части трубопровода необходимо учитывать и перемещение примыкающих к ним подземных уча стков трубопроводов.
§ 1 Определение расстояний между опорами
Прн определении изгибающих моментов для балочных систем надземных трубопроводов от действия поперечной нагрузки в качестве расчетной угодсли трубопровода принимают балку трубчатого сечения. Граничные ус лонпя на опорах зависят от способа монтажа перехода.
В практике строительства трубопроводов применяют два способа монтажа многопролетных балочных переходов. Первый способ, называемый «неразрезанным», заключается в том, что длинную плеть, равную общей длине перехода, используя трубоукладчики, укладывают па промежуточные опоры. Расчетная схема такого перехода представляет многопролетную балку При «неразрезном» способе монтажа мпогопролетного перехода : рубопровода максимальный изгибающий момент от поперечной нагрузки возникает на промежуточных опорах и определяется общими правилами
строительной механики. При равной длине средних пролетов максимальный изгибающий момент
М0 = <?/2 12 0,0833ql2, (10.1)
me q — сумма интенсивностей всех поперечных нагрузок, включая и соб
сгненный вес трубопровода (при расчете трубопровода па вертикальные нагрузки); I—расстояние между опорами
Второй способ монтажа называемый «разрезным», заключается в том. что трубопровод укладывают на опоры отдельными секциями, равными
длине одного пролета, а затем секции сваривают .между собой. Расчетная схема такого перехода при действии собственного веса представляет собой «дпопролетную балку с шарнирными опорами (концами); опорный и пролетный (посередине пролета) моменты-
де f/тр — вес единицы длины трубы.
На нагрузки, возникающие в процессе эксплуатации, трубопровод рассчитывают как многопролетную балку, т. с. опорный и пролетный моменты определяют по формулам:
М0 (q — <?тр) iZ/12; = {q-qTp) Ш. (10.3)
В зависимости от соотношения собственного веса трубы и продукта расчетным моментом может являться лнбо пролетный, либо опорный Поэтому необходимо вычислить суммарный изгибающий момент на опоре и в пролете от всех поперечных нагрузок (</тр и q—<?тР) и в качестве
I
расчетного принять больший. Длина крайних пролетов миогопролетиой[ сц стемы желательно принимать равными 80 % от промежуточных, что об( спечивает примерное равенство опорных и пролетных моментов.
При проектировании и строительстве переходов применяют одно- и< многопролетные (до четырех пролетов) консольные схемы с наклонньпГ компенсаторами по концам. Важным является выбор рациональных дли консолей.
При проектировании однопролетных двухкоисольных балочиых переходов длину консолей из условия минимума изгибных напряжений следует при нимать равной 35% от длины пролета (/г=0,35 /), в этом случае расчет! ный изгибающий момент
оР
0,0625<j/2. (10 4)
Как следует из сравнения формул (10.1) и (104), прн одной и той же длине пролета за счет разгружающего действия консолей изгибиые напря® жеиия однопролетпого перехода с двумя консолями меньше напряжений! в многопролетной системе на 33 %, т. е. применение этой системы позвоД ляст увеличить пролет на 15 %¦
AIhoi опролетную систему с консолями рассчитывают так же, как и | обычную миогопролетную систему, длину же консоли принимают равном 40 % от длины пролета.
Воздействие температурного перепада и внутреннего давления вызы^Я пает продольные напряжения, llpu расчете обычно учитывают только про-* дольные осевые напряжения, пренебрегая влиянием изгибных напряжений. !
Продольные осевые напряжения в стенках трубы перехода с компенв саторами
°пР Л/ = i?Fсв - Hk)/F • (10-5)1
где р — расчетное внутреннее давление; fc» —площадь трубы в свету; Ни—1 реакция отпора компенсатора; F — площадь сечеиия стенок трубы.
Пренебрегая отпором компепсатора и выполняя соответствующие »ре- ] образования, получаем
где Сткц — кольцевые напряжения в трубе от внутреннего давления.
Для определения пролета балочных переходов используются предельные-! состояния, установленные нормами. Для многопролетных систем прокладки* с компенсаторами при отсутствии или устранении резонансиых колебаний! перехода в ветровом потоке предельное состояние из условия образования пластического шарнира имеет
0,5ок„ + #2 1
\М |<l,27/?2tTsin —-— л, (10 7)1
где М — абсолютный максимальный изгибающий момент; W — момент со- Л противления сечения стенок трубы; о„ц — кольцевые напряжения в трубе Я от внутреннего давления; /?2 — расчетное сопротивление, определяемое cor-в ласно норм
Так как изгибающий момент зависит от длины пролета, то из условия ] (10.7) можно определить максимальное расстояние между опорами. В част-Л кости, для многопролетных систем при «неразрезном» способе монтажа 1 максимальное расстояние между промежуточными опорами
0,5aKTi 4- Ro l,27R2W sin - кч 2
Для однопролетных переходов с компенсаторами предельное состояние, установленное нормами, можио записать в виде
I М | [R2 О, ^Окц) W. (10 9)
[o'Да максимальное расстояние между опорами перехода с коисолямн бч'дст определяться по формуле
(К2-0,5окц) W 0,0625?
V-
(10 10)
Если толщина стенки труб перехода подобрана по внутреннему давле-шю так, что удовлетворяется условие aKK=i?2, то формулы (10.7) и (10.9) .преобразуются соответственно к виду:
| М |<0,9RSW;
Таким образом, использование в качестве предельною состояния условии образования пластического шарнира позволяет увеличить пролет на
30 V
Приведенные расчетные формулы определяют напряженное состояние трубопровода только от вертикальных поперечных нагрузок и внутреннего давления. При действии ветровой нагрузки в горизонтальной плоскости изгибающие моменты вычисляют по формулам (10.1) (10-4), принимая
в качестве поперечной иагруэкн ветровую. Геометрическая равнодействующая изгибающих моментов
Пролет перехода определяется аналогичным образом исходя из предельных остояннй (107) или (109).
Ветровая нагрузка при наличии резонанса вызывает изгибающий мо-иеит и в вертикальной плоскости, поэтому необходимо проверить, имеет п место для принятой схемы прокладки ветровой резонанс, и выбрать расстояние между опорами из условия предотвращения ветрового резонанса. Искомое расстояние между опорами определяется исходя из критерия, что при критической скорости ветра более 25 м/с для надземных трубопроводов отсутствует ветровой резонае [34]. Критическая скорость ветра для надземного трубопровода определяется по формуле
где ?)„ — наружный диаметр; v — частота свободных колебаний трубопровода; Sh — число Струхаля-,
Число Струхаля "для надземных трубопроводов (при отсутствии аэродинамических гасителей колебаний) определяют по формуле
Sh = 0,2 + 0,0163 — , (10.13)
А
где h — высота расположения трубопровода над поверхностью земли
Используя зависимость частоты колебаний от пролета (2.11) и приняв -’кр=25 м/с, из (211) И (10.12) находим максимальное расстояние между опорами, при котором не возникает ветровой резонанс
klElg
Приняп число Струхаля равным 0,2 При h/D„>2 п подставив значение g=9,8l, получим
(1 - mS).
(10.15>
где Е1—нзгнбная жесткость трубы, Н • м2; D,, — наружный диамет
трубы, м; kK — коэффициент, зависящий от числа пролетов; q — расчетная поперечная нагрузка, Н/м; тг — отношение продольного сжимающего усилия-к критическому.
Применение виброгаеителеП целесообразно в тех случаях, когда умепь шение длин пролетов переходов до величии, при которых не возникает резонансных колебаний, не рационально по тохнпко-экопомическим сооб ражениям. Основными способами борьбы с колебаниями надземных пере! ходов являются:
повышение демпфирования конструкции трубопровода и приложение! инерционных усилий в протнвофазе—механические способы;
устранение причин, вызывающих колебания, аэродинамические спо-lj собы;
одновременное использование указанных способов;
изменение частоты собственных колебаний путем устройства антивибрационных связей.
Характеристики механических гасителей колебаний и некоторые данные по аэродинамическим способам гашения колебаний приведены в рекомендациях (34].
При прокладке трубопроводов на пучииистых грунтах возможно перемещение опор под действием сил пучения. В статически определимых (од-нопролстных) системах вертикальные перемещения опоры не вызывают j дополнительных напряжений. В многопролетных системах при перемещении одной из опор возникают дополнительные изгибные напряжения. Их можно-определить в соответствии с известными решениями для мпогопролетных балок при заданном перемещении опоры.
Изгибающие моменты для опорного И пролетного сечения можно опре- ! делить но формулам:
1.02Е/А
МД2 =
(10 16)
4,39EIA /2
где Е1—нзгнбная жесткость трубопровода; А — относительное вертикальное перемещение опоры вверх; I—расстояние между опорами.
При одновременном действии поперечной нагрузки и пучения изгиба- , ющпе моменты суммируются Обратим внимание на то, что изгибающий момент от поперечной нагрузки пропорционален квадрату расстояния между’ опорами, а от пучения — обратно пропорционален квадрату расстояния. Сте-1 довательно, нужен пролет, при котором суммарный момент минимален. | Суммарный момент
EIД
M = k1qP+kt——¦, (10.17>
г
где ki и k2 — коэффициенты, зависящие от расчетной схемы перехода и расчетного сечения — опорного или пролетного. Определим расстояние 1 между опорами, соответствующее минимуму изгибающего момента при заданном перемещении. Минимуму соответствует условие dM/dl—О. Из (10.17), выполнив дифференцирование, найдем
k,EI А Кя
Подставив (10.18) в (10.17), найдем минимальное значение изгибающего
момента
Afmin - 2 VfeiM?/A. (10.19^
По предельному изгибающему моменту, определяемому условием 110.7). приравняв его Afmin, из (10.19) можно определить максимально допустимое пучение опоры, далее, по формуле (10 18) — максимально допустимый пролет перехода. Если фактическое значение пучения опоры Л больше максимально допустимого, а, изменяя конструкцию уменьшить его невозможно, то необходимо усилить балочную конструкцию. Если фактическое значение пучения опоры меньше предельно допустимого, то длину пролета определяют из условия (10 17), приравнивая этот момент предельном;', вычисленному по формуле (10.7).
§ 2. Расчет компенсаторов на воздействие температуры и внутреннего давления
При заданном (принятом) расстоянии между компенсаторами расчет компенсаторов сводится к выбор; их геометрических параметров из условия восприятия перемещений прямолинейной части трубопровода, обусловленных воздействием температуры и внутреннего давления. Если компснса тор расположен в месте выхода подземного трубопровода на поверхность, то перемещение, на которое должен рассчитываться компенсатор, склады вается из перемещений соответствующего открытого участка и перемещения трубопровода в месте выхода его нз грунта. Прн заданных (принятых) геометрических параметрах компенсатора расчет сводится к определению предельных перемещений, воспринимаемых этим компенсатором. Определяют ей величиной прн этом является предельно допустимый уровень продольных напряжений.
Для определения продольных напряжений в компенсаторе от продольных перемещений вычислим его податливость, т. е. перемещение его конца от единичного усилия Н. Для общности решения рассмотрим трапецеидальный компенсатор. Все принятые геометрические параметры компенсатора (а- угол поворота, р радиус оси изгиба отвода, вылет компенсатора. 1и длина полки) представлены на рис. 50. Компенсатор Представляет собой систему, состоящую из круговых отводов и прямолинейных участков. Податливость его определяется так же, как для стержневой системы:
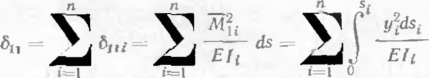
где п — число участков, которое для схемы, изображенной на рис. 50
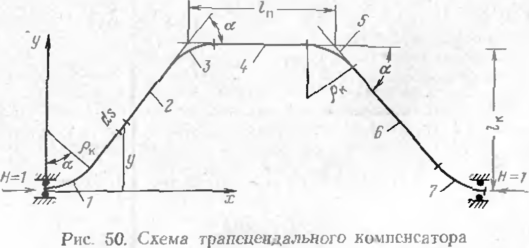
равно 7; Eli нзгибиая жесткость каждого участка; Мц — изгибающий момент от единичного усилия.
Выполнив интегрирование в соответствии с форм} л ой (10.20), получим податлииость для трапецеидального компенсатора
6,1 = ~^j~ (-?- ^ За -г 4 cos а--L sin 2а - 4 j + ?рка - 2р«iK х
2
X (а + cos а — 1)]J. -J-:—— [/3 — 2р3 (1 — cos а)3 + 3/кр2 (1 — cos а)2 —
-3/2KpK(l-co.sa)] | y2K-2P/K(l_cosa)]( (10.21)
-где km — коэффициент уменьшения жесткости отвода; а— угол попорота.
Податливость П-образного компенсатора (рнс. 51, а) можно получить из (10.21). приняв угол поворота и=я/2 и выполнив преобразования:
Ьп “ ~т~ [i~ 1,42р* 3'14р«“ 2'28р«гк)+°'67iK -1 -34Рк +
Аналогичным образом определим податливость Z-образною компенсатора, состоящего только из элементов J, 2, S (рис. 51, б):
бц .= |-?-[р«(за 4 cos а--- sin 2а - 4^.+ *2рка - 2р2 гк х
X (а -(- cos а 1) -f ——1-[/3 " 2р* 0 — cos в)3 -f- 3i р2 (1 — cos а)2 —
Змк 1 к
-3^pn(l-cosa)Jj. (10.23)
Для Z-образного компенсатора, наклоненного под углом 90° к переходу, т. е. при а=п/2 (рис. 51,в), податливость, как следует из (10.23):
6,1 ~ ~ШГ [ L + 3> 14pJ« ~~ 2-28р«1«)+ °'67!- ~1 -34рк
Податливость Г-оОразного компенсатора, состоящего только из элемента > (см. рис. 51, г), определяется по формуле
8Ч = -Г7ГГ —Г • (10.25)
(3EI sma)
При а=я/2
Г
бц - * .
(10.26>
{ЗЕ/)
Отмстим, что все формулы для частных случаев, порченные из общего решения, совпадают с формулами, приведеппьгми в СНиП II-45—75
Обозначим продольное перемещение в месте примыкания трубопровода к компенсатору, т. е. по направлению единичного перемещения Н через Д„. Гогда распор компенсатора
Як = Дк/бц. (10 27>
Зная распор компенсатора при тех же допущениях, что и ранее, опреде-иют максимальный изгибающий момент в сечении, наиболее удаленном от действия силы Нк:
Мкомп = Нк У — —г ¦ (10.28}
Оц
Максимальные продольные напряжения, возникающие в отводе компенса тора, определяют с учетом коэффициента концентрации напряжений тк по формуле
Окомп тк (10.29V
Формулы и графики для определения коэффициента уменьшений жесткости km и коэффициента концентрации напряжений тк для отводов в зависимости ог геометрических параметров приведены в гл. 15.
При определении продольных перемещений следует учитывать внут-pei иее давление только прн положите тьном температурном перепаде. В соот встсттш с предельными состояниями, которые установлены нормами, предельная величина окомп определяется условием
°комп < *2 - (°- Чц °м), (10 30>
1 ie R-J — расчетное; сопротивление, определяемое согласно СНиП 11-45—75; оКц кольцевые напряжения от расчетного внутреннего давления <тм — дополнительные продольные напряжения в компенсаторе от изгиба под дей-твнем поперечных нагрузок.
Следует учесть что при определении [оКоып] по формуле (10 30) для компенсаторов, установленных иа участках трубопроводов, работающих при «ало изменяющемся температурном режиме (на линейной части газопрово-юв, нефтепроводов и нефтспродуктопроводов), допускается согласно нормам принимать вместо расчетного сопротивления Яг нормативное сопротивление RB2
Расчет компенсаторов проводится в следующей последовательности По ПО 30) определяют предельную величину [Окомп]- Далее, возможны два Подхода Для принятой конструкции и изпеетшх геометрических парамет ров компенсатора определяют его податливость 6ц, затем из (10 29) опре леляют его компенсирующую особенность Дк Эта величина, как следует Из (10 29) и (10.30), определяется исходя из предельного состояния.
установленного нормами. По компенсирующей способности определяют расстояние между компенсаторами. Второй подход основан иа выборе параметров компенсатора необходимой компенсирующей способности.
Для трубопроводов больших диаметров продольные перемещения в месте выхода подземного трубопровода на поверхность значительны. Этн перемещения рационально уменьшать, устраивая подземные компенсаторы-уноры.
Сравним компенсирующую способность компенсаторов — трапецеидального и П-образного, выполненных из труб размером 1420x16,5 мм с применением отвода 5D„=710 см. Геометрические размеры компенсаторов: вылет компенсаторов /к = 22 м, длина полки /ц=9 м, для трапецеидального комп нсатора угол поворота а=45° (а=я/4).
Вычисляем изгнбиую жесткость прямой трубы
EI
2,1 • 107 я. [1424 — (142 — 2-1,65)4]
= 3,76- 10й Н-см2.
64
Параметр отвода
1,65-710
0,238.
t [(142—1,65)/2]2 Коэффициент уменьшения жидкости отвода при Ак<0.3
К
0,238
1,65
1,65
- 0,144..
Податливость трапецеидального компенсатора по (10.21)
(--— [710s (з — -|-
1 0,144 V 4
6ll~
~3 7С~1013' l~0l44~(U42 7103 Л
710-2200>-2.2в-710*-2200) +
— 0,67 22003 —1,34-7104 2-2200-7102 — 4-22002-710 -| 900-22002| =
1
8,78-10» +7,13 10е — 4,8-10» + 2,22-10е — 1,37 х
3,76- 10*4 0,144
X Ю10 + 4,36-109) 1,61 10-3 см/Н.
Жесткости компенсатора есть величины, обратные податливости. Жесткости трапецеидального и П-образного компенсаторов соответственно будут равны:
т]к • —— = i-— 1060 Н/см;
бц 9,44- 10-4
jik - ——--1-— -= 620 Н 'см.
61г 1,61 io-s
Из этого примера следует, что жесткость П-образного компенсатора примерно в 1,7 раза меньше жесткости трапецеидального компенсатора. Это означает, что компенсирующая способность П-образного компенсатора больше, чем трапецеидального с тем же вылетом. Это объясняется тем, что длины отподов, играющих определяющую роль в работе компенсаторов (прн прочих равных ус товиях), в трапецеидальном компенсаторе меньше, чем в ll-образном, в данном примере в 2 раза.
