Фазовое состояние природных газовых систем
ГЛАВА III
ФАЗОВОЕ СОСТОЯНИЕ ПРИРОДНЫХ ГАЗОВЫХ СИСТЕМ
Под термином «природный газ» подразумевают смесь летучих углеводородов и углеводородов, находящихся в газовой фазе. Когда говорят о сжиженном природном газе, то выражение «природный газ» относится к компонентам в омеси *. Когда говорят о газовой шапке в пласте, то имеют в виду углеводороды, находящиеся в газовой фазе над нефтью. В этом случае газовая фаза может содержать молекулы некоторых углеводородов, существующих в обычных условиях в виде вьгоококипящих жидкостей 6.
Процесс испарения жидкостей, происходящий в результате увеличения давления, создаваемого газом. — явление, обычное для условий нефтяных месторождений.
Знание фазового состояния углеводородных смесей необходимо для правильного подхода к использованию природных углеводородных систем газ —- жидкость. Цель изучения фазового поведения смесей состоит в том, чтобы, зная состав смеси, иметь возможность предвидеть количественные соотношения жидкой и газовой фаз, находящихся в равновесии, при любых значениях давления и температуры. Правильное представление о поведении индивидуальных углеводородов помогает предсказать свойства вещества, находящегося в однофазном состоянии. Знание природы простых омесей облегчает изучение поведения более сложных систем, к числу которых относятся природные газы.
§ 1. ИНДИВИДУАЛЬНЫЕ ВЕЩЕСТВА. УПРУГОСТЬ ПАРОВ
Индивидуальные вещества в зависимости от температуры и давления могут находиться в парообразном, жидком или твердом состоянии. Если вещество находится в однофазном состоянии, то его объем V будет определяться температурой вещества Т и давлением р. На рис. III. 1 [III. 66] дано соотношение pVT для индивидуального вещества в пространственной системе координат. Фазовое состояние вещества на этом рисунке изображается поверхностями среза. Вследствие того, что пользоваться такими пространственными диаграммами более сложно, чем двухразмерными, обычно при изучении фазового состояния компонентов природного газа применяют графики зависимости давление — объем (проекция диаграммы рис. III. 1 на плоскость с осями давление — объем)'при постоянной температуре (рис. 111.3) и давление— температура (рис. III. 2) при постоянном объеме.
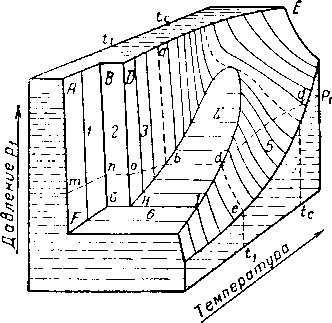
Рис. III. 1. Пространственная диаграмма давление — объем — температура для индивидуального вещества [111.66].
/ — твердое состояние: 2 — твердое состояние + жидкость; 3 — жидкость; 4 — жидкость + пар; 5 — пар; б —твердое состояние + пар.
Условия, при которых в одно и то же время часть вещества мйжет существовать в газообразном, а часть в жидком состоянии, выделены на рис. III. 1 площадью HbCdl. Линии, проведенные внутри этой площади, параллельны плоскости основания диаграммы, поэтому проекции линий СЬН или Cdl на плоскость с координатами давление — температура обращаются в одну кривую (НС на рис. III. 2), известную как кривая давле-
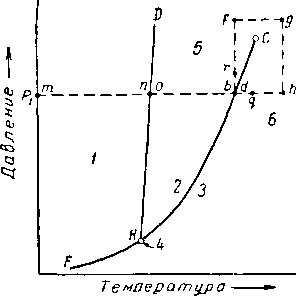
Рис. III. 2. Диаграмма давление — температура.
/ _ твердое состояние: 2 — жидкость;
3 — пар; 4—-тройная точка; 5 — сжатая жидкость; 6 — перегретый пар или газ.
«ия насыщенного пара. Поверхность, соответствующая одновременному существованию вещества в жидком и твердом состоянии, BDHG проектируется на рис. III. 2 в виде линии HD, а одновременного существования твердого тела и газа ¦— в виде линии HF. Рассмотрим состояния, через которые пройдет метан, если его температура будет увеличиваться при постоянном давлении р\ (рис. III. 1). В точке т метан будет находиться в твердом состоянии. В точке п начинает образовываться жидкость, и при подведении тепла при постоянной температуре и давлении метан превращается полностью в жидкость в точке О. Дальнейшее повышение температуры сопровождается уменьшением плотности жидкой фазы до точки 6, в которой начинается испарение метана. Процесс испарения происходит при постоянной температуре и кончается в точке d, когда вся жидкость переходит в газообразное состояние. Дальнейший подъем температуры между dag приводит лишь к увеличению объема метана без каких-либо фазовых изменений.
В точке Н одновременно существуют все три фазы При этом индивидуальный компонент может находиться в равновесном трехфазном состоянии только при значениях давления и температуры, соответствующих этой точке.
Линии, соответствующие постоянной температуре (такие, как abde на рис. III. 1), могут быть нанесены как изотермы (рис. III 3) на графике, выражающем зависимость объема от давления. Данные изменения плотности насыщенных фаз (представляющие величины, обратные удельным объемам) приведены на рис. III. 4. Необходимо отметить, что при увеличении температуры удельный объем жидкой фазы увеличивается (плотность уменьшается), а объем газообразной фазы, наоборот, уменьшается (плотность растет), причем в критической точке С их удельные объемы и плотности становятся одинаковыми. В точке, соответствующей критической температуре и критическому давлению, становятся одинаковыми и все другие свойства обеих фаз.
Если на графике рис. III. 4 провести линию среднего значения плотностей насыщенного жидкостью газа и насыщенной газом жидкости, то эта линия пересечет кривую плотности в критической точке. Этот факт известен под названием правила прямолинейного диаметра, а методика предложена Кайлететом и Матиасом (Cailletet and Mathias) в 1886 г. [III. 12]. Изучение явления и обзор свойств углеводородов в критической точке сделаны Кобе и Линном (Кове and Lynn) [III. 38].
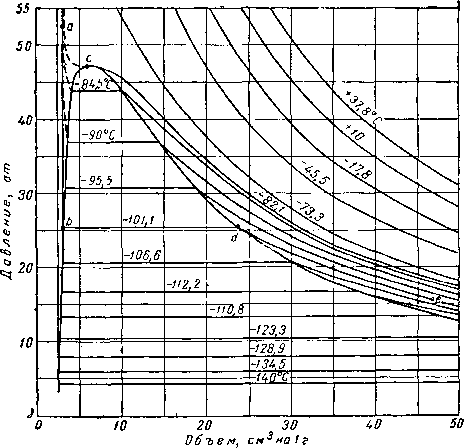
Рис. III. 3. Диаграмма давление — объем для метана [111.42].
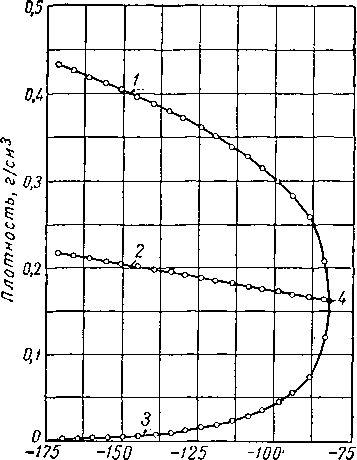
Температура, °С
Рис. 111.4. Ортобарическая плотность метана [111.37].
/ — насыщенная жидкость; 2 — средняя плотность; 3 — насыщенный пар; 4 — критическая точка.
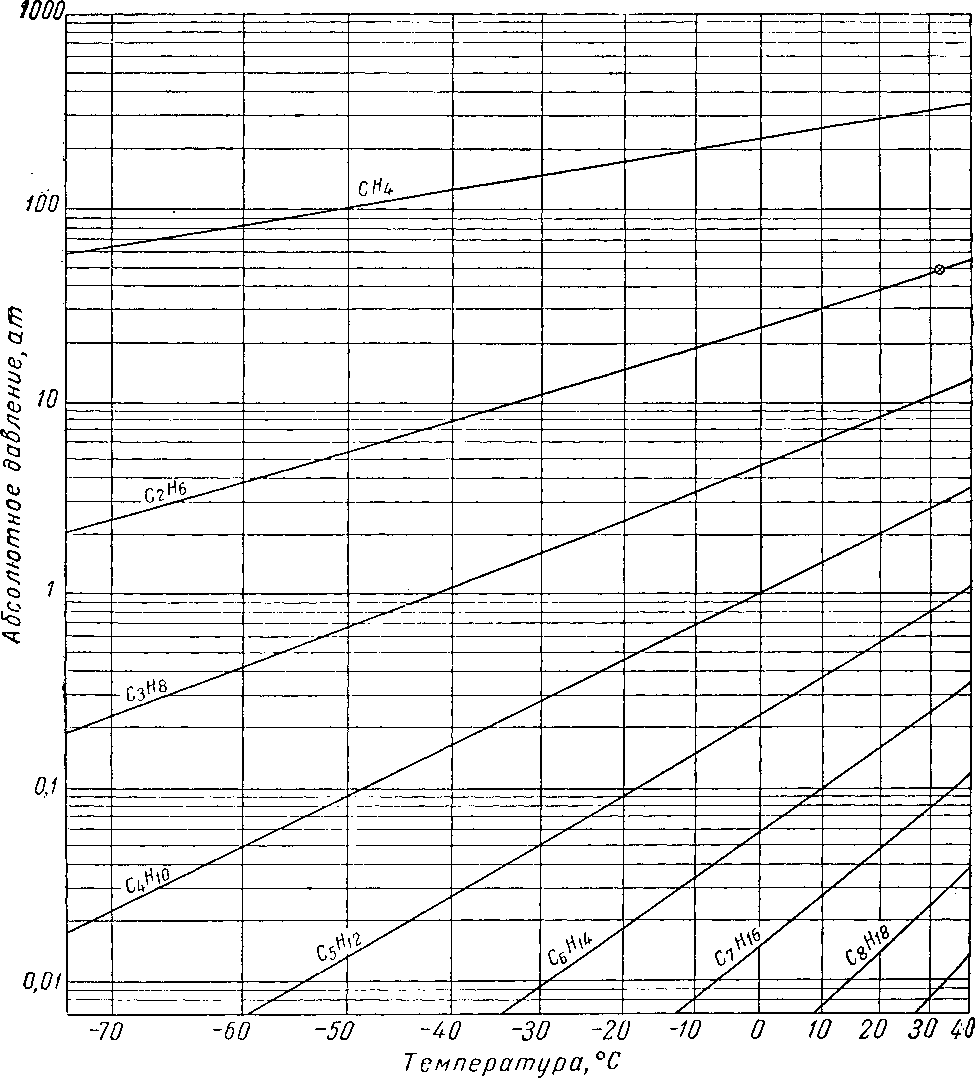
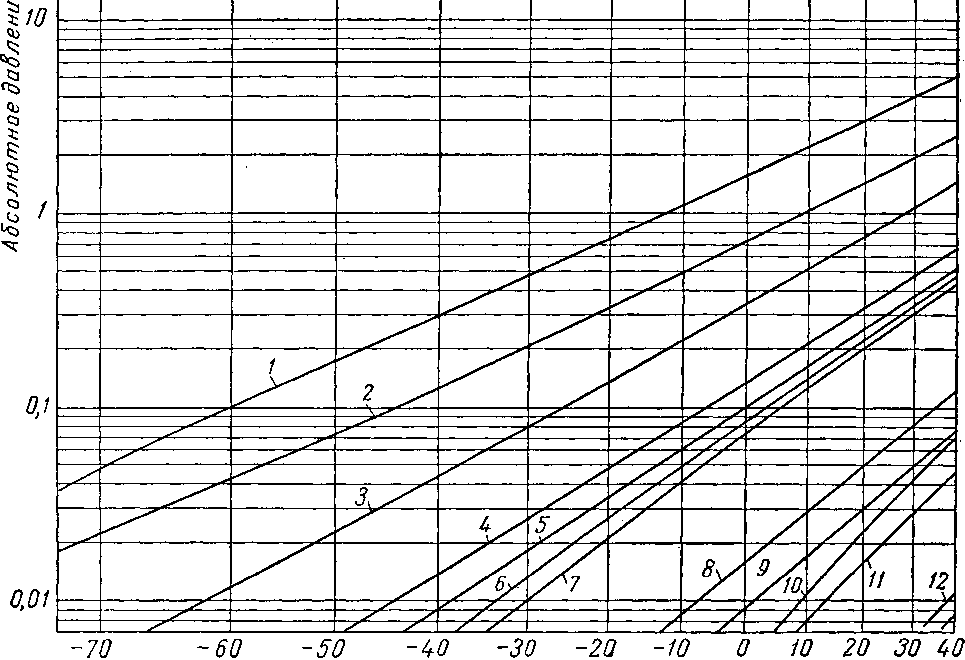
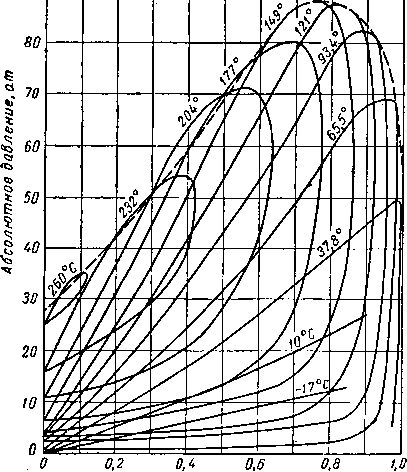
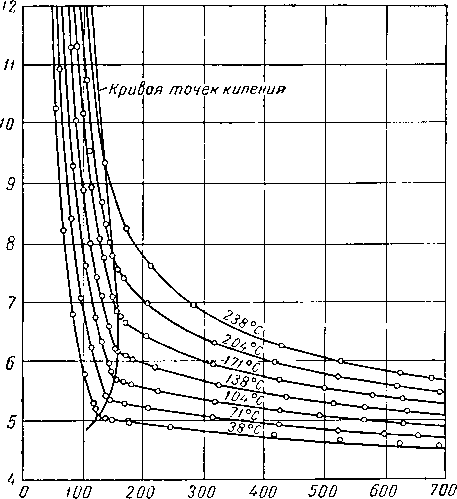
Наиболее важные свойства индивидуальных веществ выражаются кривой упругости пара, представляющей зависимость температуры кипения от давления. Индивидуальные углеводороды встречаются в различных технологических процессах или в лабораторных исследованиях, поэтому необходимо знать характер кривых упругости пара. На рис. III. 5 и III. 8 приведены кривые упругости пара различных легких углеводородов, встречающихся в газовой промышленности.
Г e мпература, °C
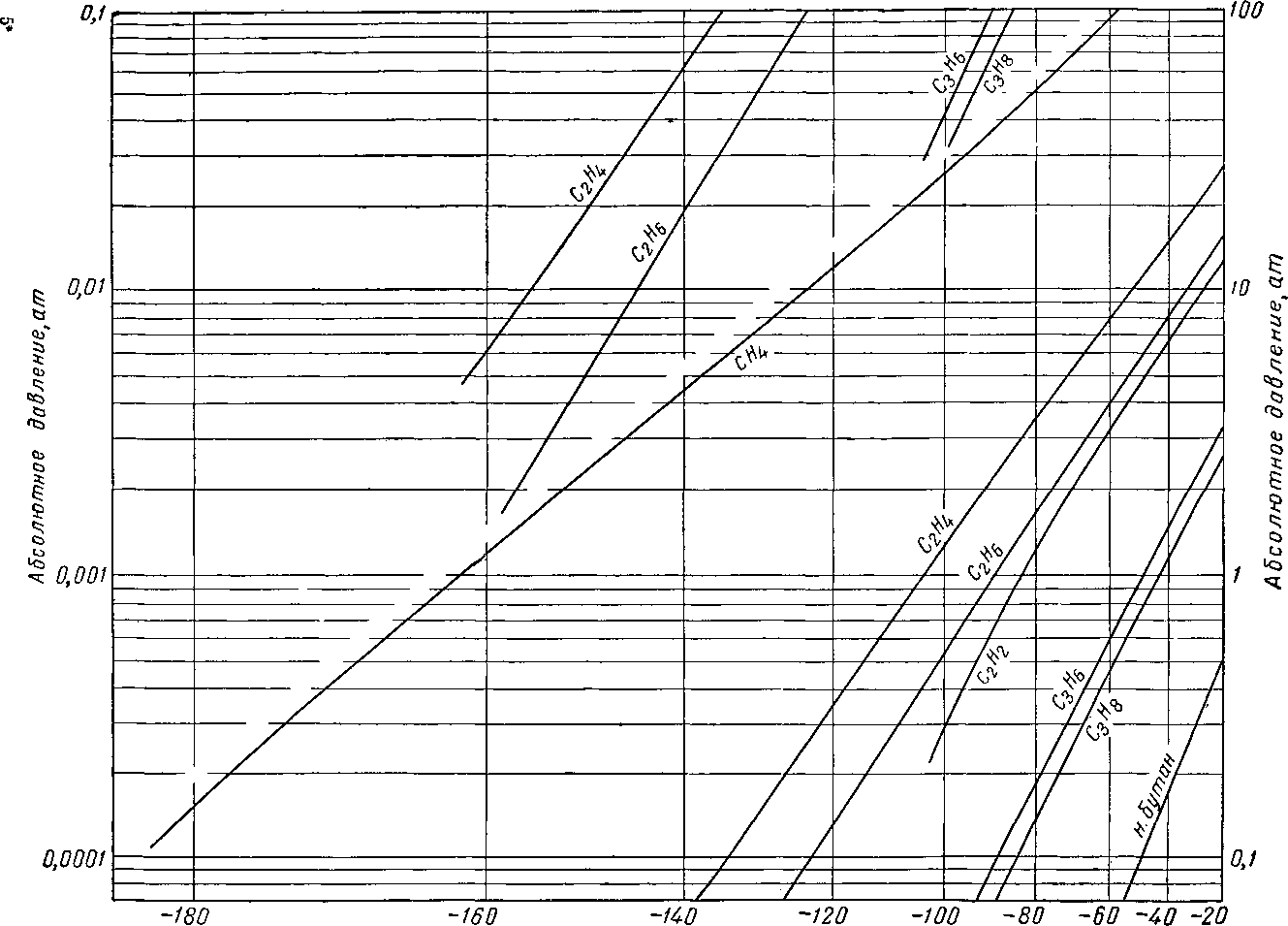
Рис. III. 7. Упругость паров для газов при низких температурах.
CD
UO 50 60 70 80 90 100 150 200 250 300 350 Ш 500
Температура, °С
Абсолютное даВление,ат
метановых углеводородов.
roo
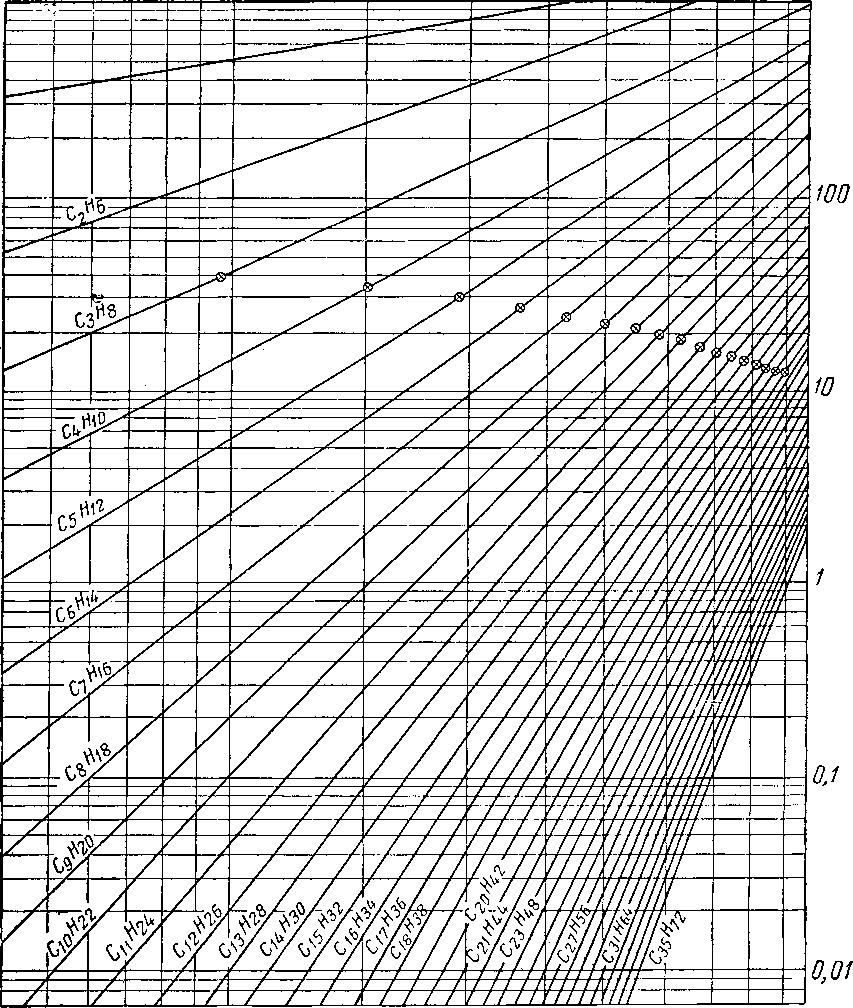
Рис. HI. 6. Упругость паров метановых
j _ изобутан, 2-метилпропан; 2 — нсопснтан, 2,2-диметилпропан;
5 — диизопропил, 2,3-диметилбутан; 6 — 2-метилпентая; бутил, 2,5-диметилгексан; № — 2, 2, 3, 3-тетраметилбутаи;
метилоктан; 14 — 2,7-диметилоктан;
UO 50 60 70 80 90 100 150 200 250 300 350 Ш 500
moo
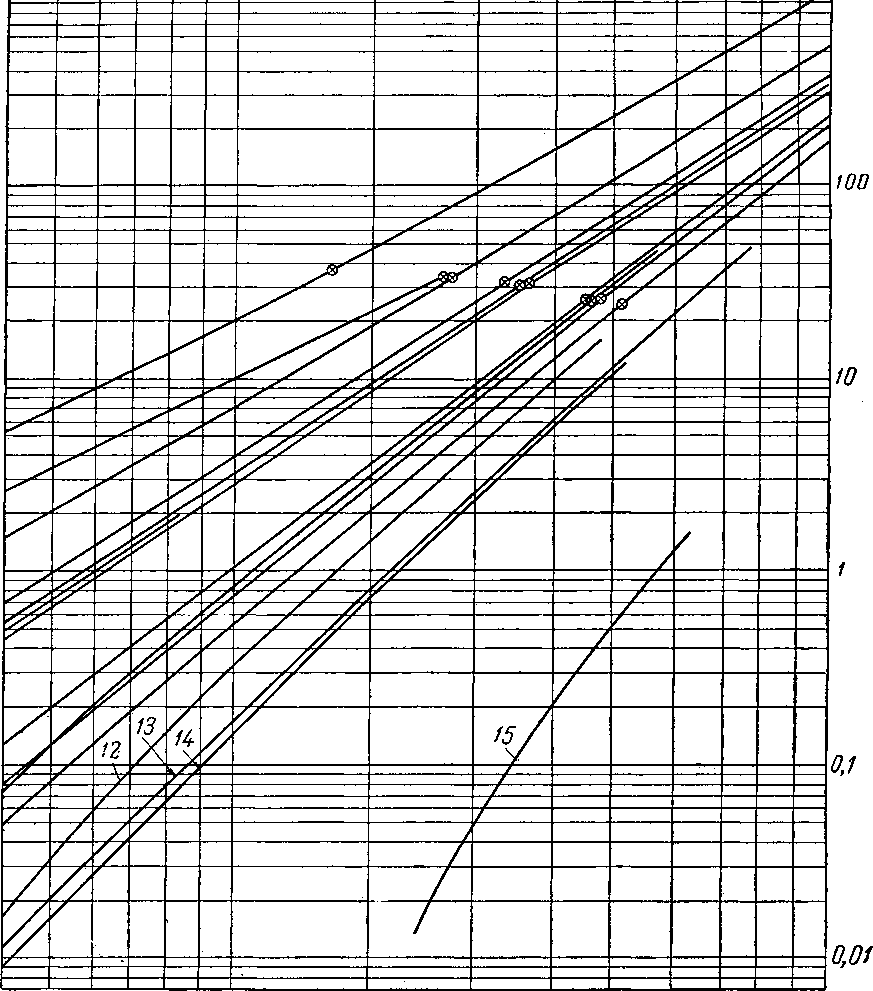
Абсолютное даВление,ат
углеводородов изомерного строения.
3 — нзопентан, 2-метилбутан: 4 — неогексан, 2,2-диметилбутап;
7 — 3-метилпентан; S — изооктан, 2. 2, 4-триметилпентан; 9 — диизи» // — 2. 2. 4,4-тетраметилпентан; 12 — 3-3-ДЧЭТИЛпентан; 13 — 2.6-ди-15 2-метилгептэдекац.
-70 -60 -50 -UO -30 -20 -10 0 10 20 30 У)
100
Абсолютное давление, am

Рис. III. 8. Упругость паров
/ — этилен С2Н4 На; 2 — ацетилен С2Н2; 3 — пропилен С*Н8; 4 — аллен С3Н3; пропадиен; 5 — метилацетилен СзН4; ц«с-2-бутен-2(С4Н8); II — бутии-С4Нв1; 12 — иентен-1 С 8Н1в; 13 — пентадиен- СвНв1.4 ; 14 — 2-метилбутадиен
19 — гексен-СвН,г2 ; 20 н-гептен-1 CyHi4; 21 — гептен С7Н143; 22 — 3.4-ДИэтилгексаДиен-1,5 С юНм;
27 — ундекен-1 СцНаа; 28 — ундекен-1
&Q 50 60 70 80 90 100 150 200 250 300 350 ЬПО 50В
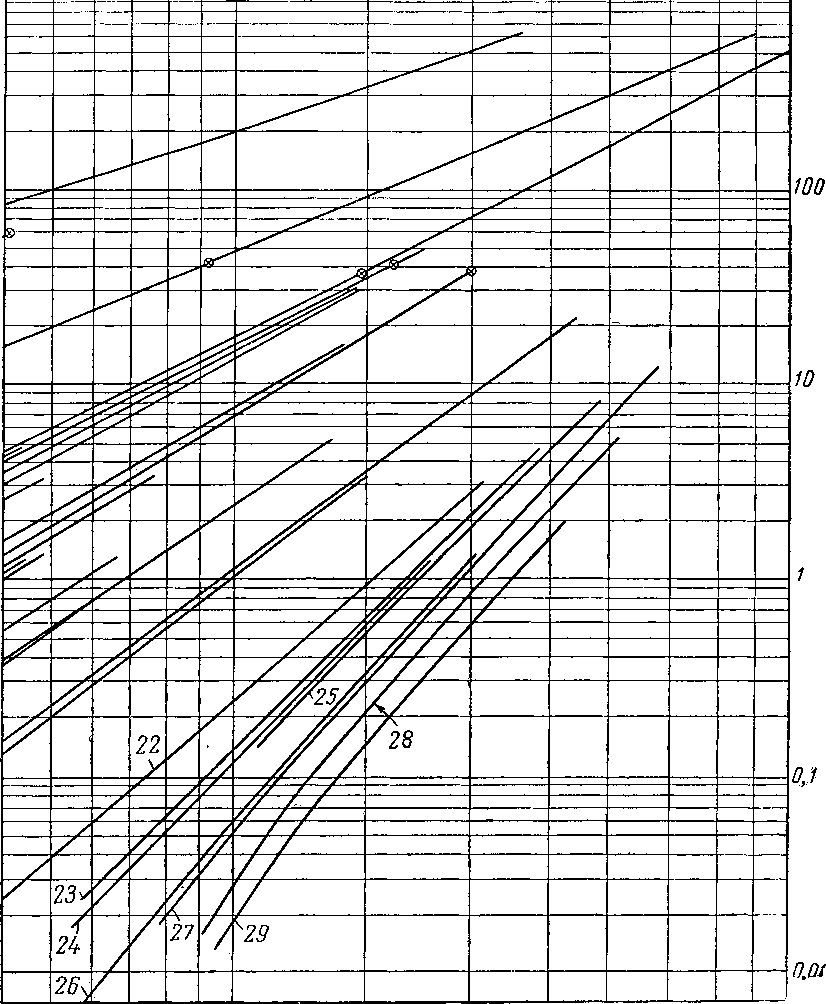
Абсолютное давление ат
Т емлература,°С
непредельных углеводородов.
6 — изобутилен, 2-метилдропан С4Н„ ; 7 —бутен-1 С„118; 8 — бутадиен-СчНв 1, 3; 9 — гронс-бутен-2 (С4Ня); 10—
С5НЯ; 15 — пентен-2 С,Н1Л; 16 — 2-метилбутен-2 С,Н,,,; 17 — 2,5-диметилгексадиен-1,5 CiHlt; is — гексен-СвН121; 23 — диизоамилен С,„Н2(,, 24 — декадиен- С1вН,в 3,7; 2Ь — декен - С10Н20; 26 — декии-С10Н181;
29 — ундекин-1 С i г1'1*»-
Правило фаз, впервые сформулированное Уиллардом Гиббсом (J. Willard Gibbs) в 1876 г. [III. 14, III. 21], является важнейшим инструментом изучения фазового состояния. Это правило применяется к системам, находящимся в условиях равновесия. Состояние равновесия между фазами может быть достигнуто или путем длительного выдерживания системы при постоянных давлениях и температуре, или путем интенсивного перемешивания системы. В условиях равновесия каждая фаза системы однородна по своему составу. Отдельные ком. попенты из одной фазы в другую не переходят. В газовой и нефтяной промышленности большое количество систем газ — жидкость практически находится в состоянии равновесия. Но даже если система не находится в состоянии равновесия, законы, управляющие равновесием, накладывают на систему определенные ограничения. Если разные фазы находятся в равновесии друг с другом, то говорят, что фазы находятся в состоянии полного взаимного насыщения.
Правило фаз обычно выражается следующим уравнением:
C + 2 — P = F, (III. 1)
где С — число независимых компонентов; Р — число фаз; F — число переменных величин, необходимых для определения состояния системы в условиях равновесия, или число степеней свободы.
Кейс (Case) [III. 14] указывал, что «правило фаз является простым средством решения некоторых химических и физических задач с помощью простых алгебраических действий» и что «число независимых уравнений должно быть равно числу переменных, чтобы из этих уравнений можно было найти значения этих переменных». Степени свободы для системы учитывают температуру, давление и состав фаз. Для системы, состоящей из двух или более фаз, концентрация входящего в нее компонента не относится к числу переменных правила фаз, хотя концентрация в данной фазе является переменной правила фаз.
Индивидуальные вещества, находящиеся в трехфазном состоянии, имеют нуль степеней свободы; это состояние выражается инвариантной (единственной) тройной точкой на соответствующей диаграмме. Индивидуальные вещества, находящиеся в двухфазном состоянии (например, пар и жидкость), имеют одну степень свободы. Так, на кривой упругости пара (рис. III. 2) давление или температура полностью определяют состояние системы. Например, при температуре 38° С пропан, находящийся в равновесном двухфазном состоянии, имеет давление 13,2 ат, плотность жидкой фазы составляет 0,477 г/см\ а плотность паровой фазы 0,027 г/см3. При этом поверхностное натяжение на границе раздела фаз равно 5,5 дин/см. Для определения всех свойств системы при условии, что система двухфазная, достаточно задаться одним лишь значением температуры. Необходимо отметить, что правило фаз касается только природы фаз и не зависит от количества вещества.
Двухкомпонентные системы, находящиеся в двухфазном состоянии, имеют две степени свободы. В этом случае состояние системы будет определяться температурой и давлением. Для определения состояния трехкомпонентной системы, существующей одновременно в виде жидкости и пара, необходимо знать температуру, давление и какое-либо переменное, характеризующее состав фаз. Этой величиной может быть концентрация одного компонента в какой-либо фазе или (что бывает чаще) отношение концентрации одного компонента к концентрации другого компонента. Для определения системы природного газа, состоящего из семи компонентов и находящегося в двухфазном состоянии, требуется знание семи переменных: температуры, давления и пяти значений концентрации компонентов в какой-либо фазе. Обычно известны только давление и температура многокомпонентных смесей и неизвестны концентрации компонентов в фазах. При определении фазовых соотношений смеси по температуре и давлению удобнее исходить из предположения, что смеси подчиняются законам идеальных растворов.
§ 3. НЕПРЕРЫВНОСТЬ ПАРОВОЙ И ЖИДКОЙ ФАЗ
Термины «пар» и «жидкость» удобно использовать для того, чтобы разграничить более плотную фазу от менее плотной. Однако при критических условиях разница между паровой и жидкой фазами исчезает.
В 1869 г. Томас Андрьюс (Thomas Andrews) [III. 3] прочёл лекцию «о непрерывности газообразного и жидкого состояния вещества», в которой указал, что «обычнее газовое состояние и обычное жидкое состояние являются по существу резко отдельными формами материи существования одного и того вещества и из одного состояния в другое можно перевести вещество путем постепенного перехода без разрыва непрерывности».
В подтверждение этой мысли рассмотрим изменение состояния метана (рис. III. 2). В точках, лежащих на линии НС (рис. 111.2), пар и жидкость существуют одновременно. Если от этой смеси в точке bd отводить тепло, то количество жидкости в смеси будет увеличиваться. Когда же вся смесь превратится в жидкость, температура начнет понижаться. Поэтому вполне естественно, что площадь, расположенная выше и левее кривой НС, соответствует жидкому состоянию. Область же, расположенная по другую сторону от кривой НС, соответствует парообразному состоянию и на рисунке обозначена как пар. Чтобы проиллюстрировать положение о том, что термины «пар» и «жидкость» служат для характеристики менее плотной и более плотной фаз в случае, когда вещество находится в двухфазном состоянии, а не для описания однофазного состояния вещества, рассмотрим жидкость в точке Ь (рис. III. 2) и поведение системы при изменении условий по траектории brfghqd. В точке Ь система находится в жидком состоянии. При движении системы по вышеуказанной траектории не имеется никаких фазовых изменений. Находится ли вещество в точке d в состоянии пара? Если да, то каким образом жидкость из точки Ь переходит в парообразное состояние в точке d без каких-либо изменений?
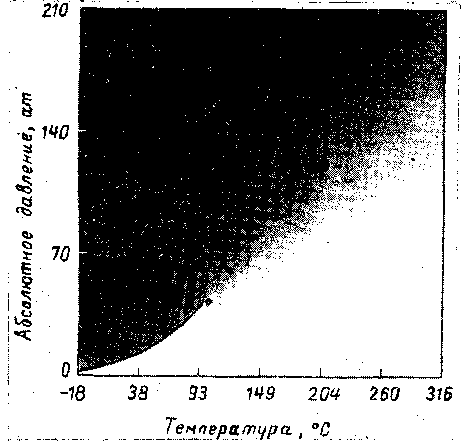
Чтобы иллюстрировать непрерывность паровой и жидкой фаз в закритической области, на рис. III. 9 приведена диаграмма давление — температура р—Т, на которой фазы различаются интенсивностью окраски. Чем слабее окраска, тем менее плотной является фаза. Резкое различие в фазах наблюдается лишь вдоль кривой и исчезает в критической точке.
Состояние чистого вещества, находящегося в закритической области при высоком давлении, удобнее назвать однофазным, так как применение терминов «пар» или «жидкость» без указания значений плотности или других свойств может привести к заблуждению. В об*
ласти на рис. III. 2, обозначенной «жидкость», вещество может быть названо сжатой жидкостью, а при температурах, превышающих температуры, соответствующие кривой давления насыщенного пара, — перегретым паром. Однако по мере приближения условий, в которых находится вещество, к критическим (критическая температура и давление) эти термины становятся менее определенными. Термины «газ» и «пар» являются равнозначными. Термин «пар» может иметь значение, обозначающее близость вещества к жидкому состоянию, а термин «газ», наоборот, отдаленность состояния вещества от условий образования жидкости. Иногда термин «газ» используется для названия состояния вещества, находящегося при температуре выше критической, а термин «пар» для обозначения состояния вещества, находящегося при температуре ниже критической, т. е. состояния, при котором вещество путем повышения давления можно перевести в жидкость.
Рис. III. 9. Непрерывность парообразного и жидкого состояний [111.28].
Одним из первых фазовое состояние смеси веществ в критической области исследовал Кюнен (Kuenen) в 1892 г. [III. 39, 111.28]. Он изучил фазовое состояние смеси углекислого газа с метилхлоридом. Кюнен заметил, что изменения фазовых состояний смесей веществ отличаются от изменений фазовых состояний индивидуальных веществ. Эти аномальные явления он назвал ретроградными [111.28]. В качестве иллюстрации на графике рис. III. 10 показано изменение состояния угле-
от точки К до точки В не вызывает появление второй фазы, а соответствует однофазному состоянию вещества. В точке В, названной точкой кипения, в жидкости появляются пузырьки пара, находящиеся в равновесии с жидкостью. При дальнейшем уменьшении давления содержание пара возрастает, достигая 20% по объему в точке F. Точки кривой ABC называются точками кипения смеси.
С другой стороны, увеличение давления при постоянной температуре от точки J до точки Е также соответствует однофазному состоянию вещества. Начиная с точки Е, в паровой фазе начинают образовываться капельки жидкости, находящиеся в равновесии с паровой фазой. Дальнейшее увеличение давления, начиная от точки Е, приводит к увеличению количества жидкости, конденсировавшейся из паровой фазы. Уменьшение давления от точки L до D также приводит к появлению капелек жидкости в паровой фазе. Кривая EJDC называется кривой точек росы. Уменьшение давления от точки М до точки С приводит к внезапному изменению состояния вещества. Из однофазного состояния в точке М вещество переходит в точке С в двухфазное, состоящее примерно на 50% из пара и на 50% из жидкости. Это получается потому, что свойства пара вдоль кривой точек росы и свойства жидкости вдоль кривой точек кипения меняются таким образом, что становятся в точке С одинаковыми. Точка С называется критической точкой смеси. Физически критическую точку найти очень трудно, и поэтому эта точка быстрее находится графически как точка пересечения кривых точек кипения и точек росы с линиями процентного содержания жидкости в смеси.
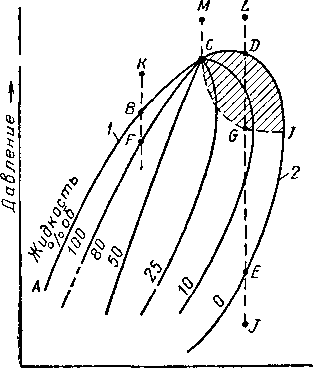
Температура
Рис. III. 10. Диаграмма фазового состояния смеси.
водородной смеси. Внутри кривой ABCDITE смесь находится в двухфазном состоянии (пар и жидкость). Вне этой кривой вещество находится в однофазном состоянии. Уменьшение давления при постоянной температуре
Сжатие индивидуальных веществ, находящихся в парообразном состоянии, до кривой давления насыщенного пара приводит к образованию капелек жидкости, т. е. поведение системы от точки J до точки Е является обычным для индивидуального вещества. Необычным является поведение смеси веществ при переходе из точки L в точку G через точку D. В этом случае в отличие
от индивидуальных веществ при снижении давления из паровой фазы образуется жидкость. Явление образования жидкости при изотермическом расширении однофазного вещества называется ретроградной конденсацией [III. 28]. При расширении от точки D до / максимально увеличивается процентное содержание жидкой фазы в точке G при данной температуре системы. При дальнейшем уменьшении давления жидкая фаза начинает нормально испаряться целиком, переходя в точке Е в паровую фазу. Во время увеличения давления в смеси от точки G до D при постоянной температуре жидкая фаза также испаряется. Этот процесс испарения жидкости, происходящий при повышении давления, йазывает-ся ретроградным испарением. Этот термин применяется при испарении жидкости, происходящем в процессе сжатия системы пар — жидкость. Терминами «ретроградная конденсация» и «ретроградное испарение» можно характеризовать и изобарический процесс для смеси, в котором изменение фазового состояния обратно изменению фазового состояния, имеющего место при тех же условиях для индивидуального вещества. На рис. III. 10 заштрихованная площадь CDIGC представляет собой единственную область диаграммы, соответствующую ретроградным явлениям.
В веществе, находящемся вблизи критической точки, происходит изменение цвета. Это явление известно под названием критической опалесценции [111.70]. Видимо, молекулярная агрегация, хотя и недостаточна для разделения смеси на фазы, все же вызывает рассеяние света. При уменьшении давления от значения, соответствующего однофазному состоянию, до давления, соответствующего граничной кривой вблизи критической точки, система окрашивается в красновато-коричневый цвет в проходящем свете или в светло-голубой цвет в отраженном свете. В небольших пределах изменения давления окраска сохраняется в обеих фазах. Сравнительно более интенсивно окрашены смеси, содержащие более высококипящие углеводороды. Интенсивность окраски является наибольшей при критической температуре и еще может наблюдаться при температуре, отличающейся от критической на 17—22°С.
ГАЗОВ в жидкостях
В литературе имеются данные о растворимости газообразных компонентов в жидкостях. При определении растворимости газов испарением жидкостей пренебрегали. Однако было установлено, что летучестью жидкости при высоких давлениях пренебрегать нельзя и, следовательно, в этом случае необходимо рассматривать состав обеих фаз системы. До 1896 г. Виллард (Villard) [111.72] провел уникальные эксперименты, в которых он наблюдал испарение брома, йода и парафина при повышении давления, создаваемого метаном, до 280 ат. Эти эксперименты указывали на возможность растворения жидкостей и твердых тел в газах. Мергам и Кобе {Markham and Kobe) приводят сведения о растворимости газов в жидкостях при низких давлениях [III. 41а].
В работе Дау и Калкина (Dow and Calkin) [III. 18] исследована растворимость природного газа в нефти. Изучению растворимости метана в различных углеводородных жидкостях посвящена работа Сэджа и Леси (Cage and Lacey) [111.59]. Фролих (Frolich) с соавторами определяли растворимость метана, водорода и азота в различных жидких смесях [III. 20]. Скоч (Schoch) с соавторами исследовал влияние химической природы растворителя на растворимость метана [111.65].
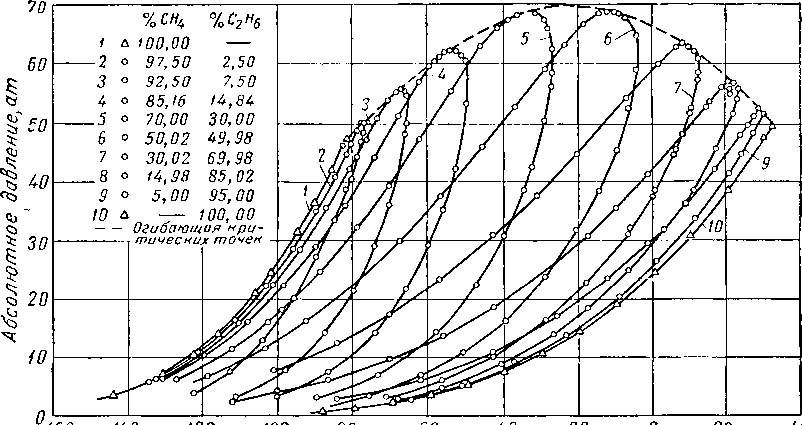
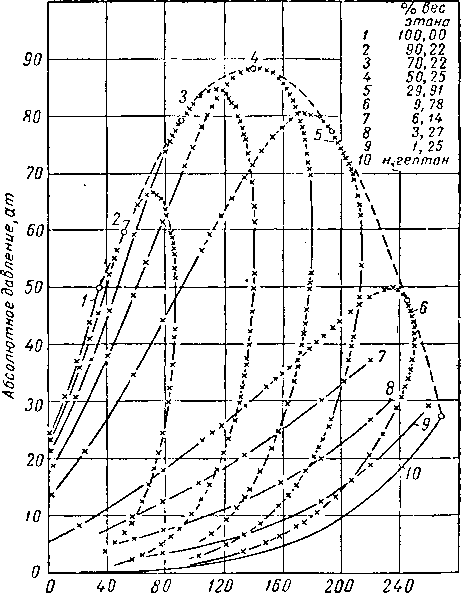
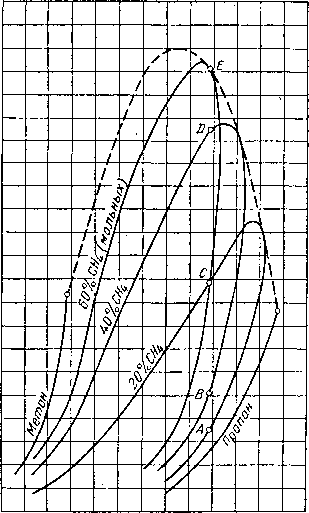
На рис. III. 11 показано поведение всех возможных смесей системы метан — этан по данным Блюмера, Гами и Парента [III. 8], на рис. III. 12 поведение системы метан — пропан по данным Сэджа, Леси, Скаафсма [III. 58], а также Акерса, Бюрнса и Файрчилда [III. 1], а на рис. III. 13 систем этан — гептан по данным Кея [111.30]. Критические температуры двух индивидуальных веществ соединяются кривой, проходящей через критические точки, соответствующие различным смесям этих двух веществ. Кривые давления насыщенного пара и огибающая кривая критических точек ограничивают область двухфазного состояния для всех концентраций смесей двух веществ.
Необходимо указать, что область двухфазного состояния смеси, содержащей сравнительно небольшое количество одного компонента, на графике типа рис. III. 11 представляется узкой полосой, ограниченной соответствующими кривыми. Бинарная смесь, состоящая примерно из одинаковых количеств компонентов, существенно расширяет свои границы. Диаграмма двухфазного состояния бинарной смеси компонентов с резко отличающимися температурами кипения распространяется на более широкую область. Поэтому для смесей, содержащих метан, диаграммы двухфазного состояния р—Т будут более широкими.
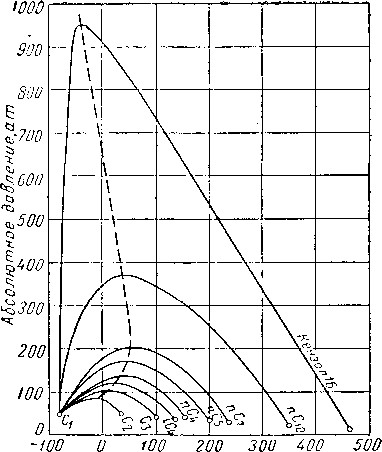
Критическое давление смеси выше критических давлений входящих в нее индивидуальных компонентов. На рис. III. 14 представлены огибающие кривые бинарных систем, содержащих метан. Чем больше разница в точках кипения двух веществ, тем выше будет подниматься критическое давление бинарной системы по сравнению с критическими давлениями обоих компонентов. Смеси метана с деканом [III. 60] будут находиться в двухфазном состоянии при давлениях выше 350 ат. Данные Рзаза и Катца [III. 57] показывают, что двухфазная область смеси метана с углеводородной фракцией, выкипающей в интервале температур 297—309° С (молекулярный вес 247), может превысить давления 700 ат. Огибающие критические кривые для различных бинарных систем даны на рис. III. 15.
Обычно принято представлять данные фазового состояния бинарных систем в виде изотерм на диаграмме давление — состав системы или изобар на диаграмме температура — состав системы, как это сделано для бинарных систем на рис. III. 16, III. 17 и III. 18. Значения плотности насыщенных пара и жидкости системы этан — гептан, полученные Кеем (Kay) [Щ. 30], приведены на рис. III. 19.
-160 -КО -120 -100 -80 -60 -ЬО -20 0 20 ЬО
Рис. III. 11. Диаграмма фазового состояния смесей метан — этан [III. 8].
по 100 90 80 70 ВО 50 40
Ю U
280
80 120 /60 200 Температура, °С
Абсолютное давление,ат
-120 -80 -40 0 40 80 120
Температура °С
30 20 10
О
Рис. III. 12. Диаграмма фазового состояния смесей метан — пропан [III.
58, III. 1, III 53].
Рис. III. 13. Диаграмма фазового состояния смесей этан — гептан [III. 30].
Т емпература, ° С
Рис. III. 14. Огибающие критических точек бинарных систем, содержащих метан [III. 57].
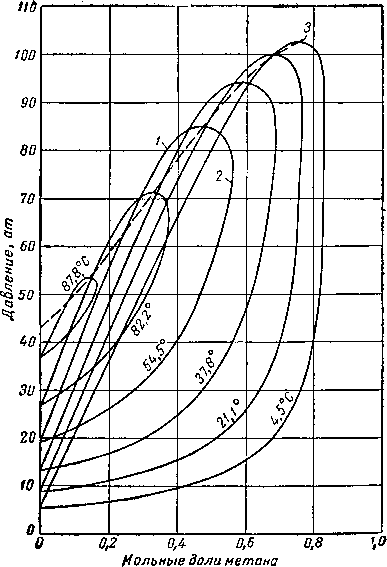
Рис. III. 16. Диаграмма давление — состав для системы метан—пропан [111.53].
1 — кривая точек кипения; 2 — кривая точек росы; 3 — огибающая критических точек.
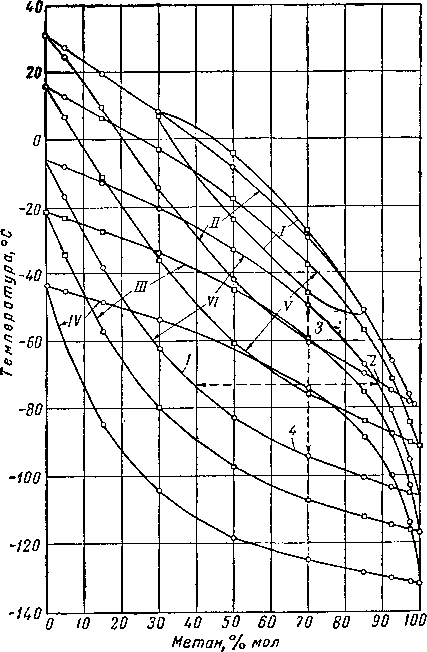
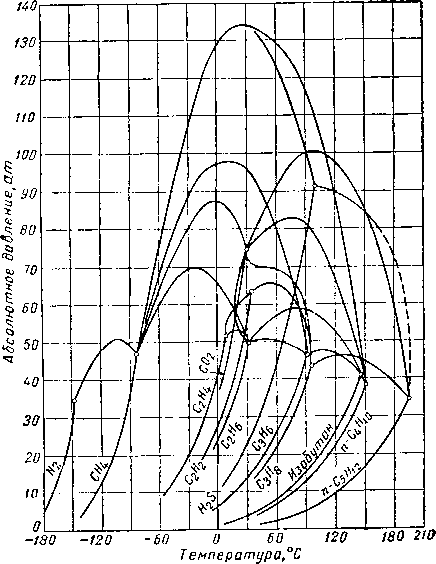
Рис. III. 1'5. Огибающие критических точек для различных систем [I. 16, I. 17, I. 9, III. 62, I. 2,
III. 17, III. 7, III. 8, III. 48, 111.43].
Рис. III. 17. Диаграмма температура — состав для системы метан —этан.
1 — насыщенная жидкость; 2 — насыщенный пар; 3~ точка росы; 4 — точка кипения. Абсолютные давления в ат: Г— 63; 77 — 49; 77/- 14; IV — 7, V — 35, VI — 21.
Этан, % мол
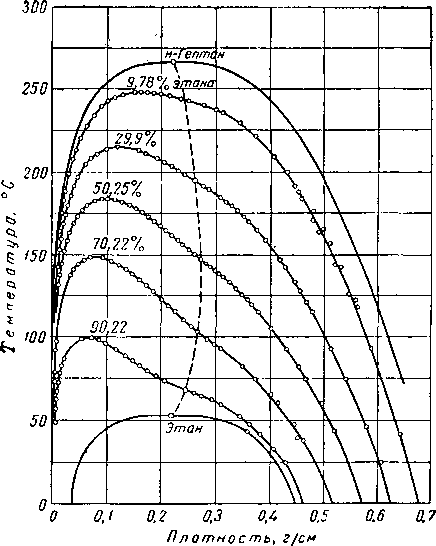
Рис. III. 18. Диаграмма давление — состав для системы этан — гептан [III. 30].
Рис. III. 19. Плотность фаз для системы этан — гептан [111.30].
§ 7. ТРОЙНЫЕ И МНОГОКОМПОНЕНТНЫЕ СИСТЕМЫ
Тройные системы являются промежуточными между бинарными и многокомпонентными и потому имеют некоторые дополнительные свойства по отношению к первым и обладают уже в некоторой степени сложностью последних.
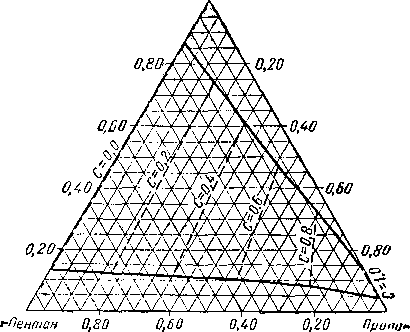
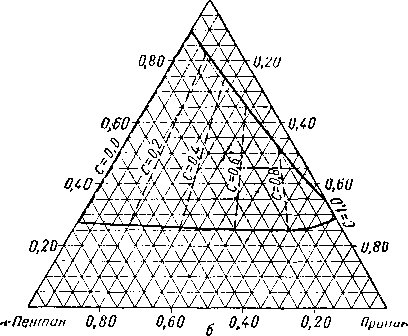
Из тройных систем наибольший интерес представляют системы метан — пропан — пентан [III. 133] и метан бутан — декан [III. 51, III. 52], изученные Седжем, Леси (Sage and Lacey) и соавторами. Фазовое состояние тройных систем при постоянных давлении и температуре удобно изображать в виде треугольных диаграмм. Такие диаграммы для трех значений давления приведены на рис. III. 20. Эти диаграммы показывают, что увеличение давления приводит к сокращению двухфазной области. Огибающие критические кривые для различных систем, характеризующихся параметром, численно равным отношению концентрации пропана к суммарной концентрации пропана и пентана, приведены на рис. III. 21. Диаграмма давление — состав для этой системы приведена на рис. III. 22.
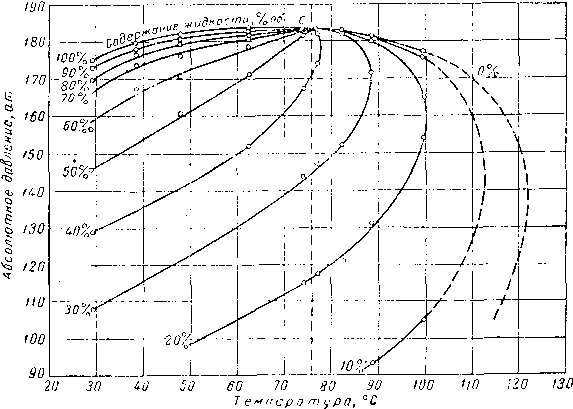
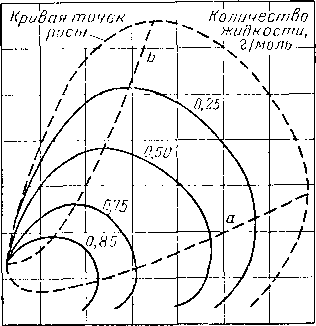
При исследовании системы метан — бутан — декан Ример, Седж и Леси (Reamer, Sage and Lacey) [111.52] приводили эксперименты при давлении и температуре, достигающих давлений и температур, существующих в газовых пластах высокого давления. Поведение этой системы иллюстрируется диаграммами, приведенными на рис. 111.23, 111.24 и 111.25. Существует лишь небольшое число фазовых диаграмм для сложных смесей, построенных на основании экспериментальных данных в форме количественного соотношения жидкости и газа, находящихся в равновесии. На рис. 111.26 представлена диаграмма, полученная Катцем, Винком, Давидом, использовавшими для ее составления визуальные наблюдения за поведением смеси природного газа с природным газолином, помещенной в камеру со смотровым окном. Состав смесей, использованный при построении указанной выше диаграммы, а также диаграмм, приводимых ниже, дается в табл. III. 1 [III. 29, 1.37]. Фазовое поведение смеси углеводородов, отобранных из газовой скважины, определялось Бакли и Лайтфутом (Buckley and Lightfoot) [III. 11] с помощью сепаратора. Результаты этих экспериментов, выражающих количество конденсировавшейся жидкости, представлены на рис. III. 27. Изучение фазового поведения проб конденсата и нефти будет рассмотрено ниже.
Рис. III. 20. Диаграмма фазового состояния системы метан — пропан — пентан при 71° С [III. 17].
а — абсолютное давление 35 ат, Т = 71° С: Ь — абсолютное давление 70 ат, Т = 71° С; с — абсолютное давление 105 am, Т = 71° С;
г.= .
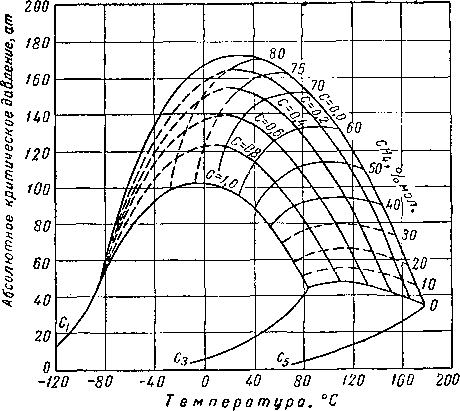
Рис. III. 21. Огибающие критических точек для системы метан—пропан— пентан [III. 13; III. 17]. с „ -?•- .
а
Метам
Сз-}-пСв
Метан
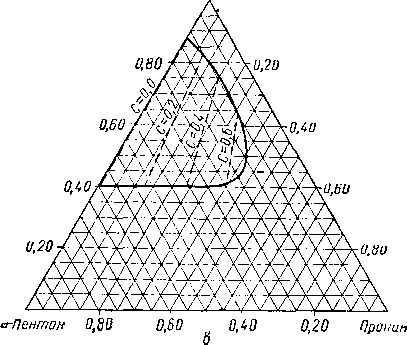
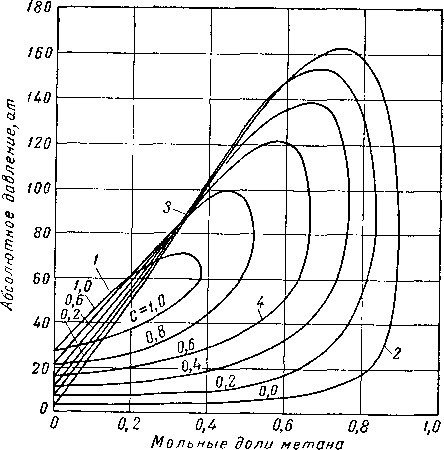
Рис. 111.22. Диаграмма давление — состав для системы метан — пропан — пентан [III. 17].
I — метан — пропан; 2 — метан — «-пентан; 3 — кривая
Сз
точек кипения; 4 — кривая точек росы; С = -р,—j—7^—
Рис. III. 24. Диаграмма давление — объем для системы, состоящей из
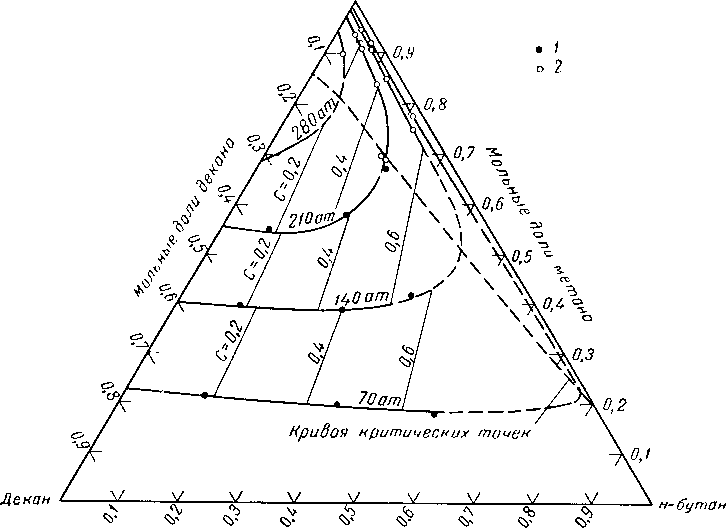
Мольнь/е доли н-бутано Рис. III. 23. Состав сосуществующих фаз для системы метан — н-бутан — декан
при 138° С [111.52].
1 — по объемным измерениям; 2 — по данным состава фаз.
Объем, смЗ/моль W
Давление, ат
0,4265 мольных долей метана, 0,249 к-бутана и 0,288 декана; С = 0.4Ю [III. 52].
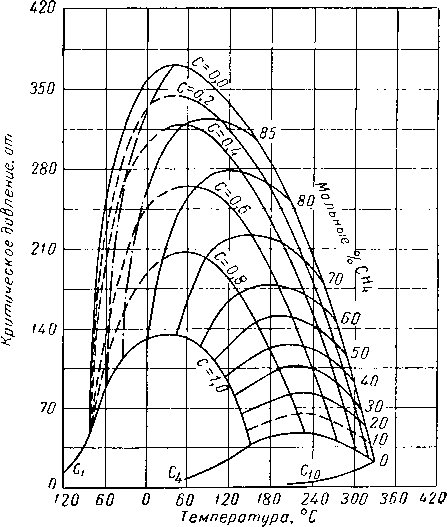
Рис. III. 25. Критические условия для системы метан— н-бутан — декан [I. 17, III. 52, III, 60].
С,
С =
ь
Рис. III. 26. Диаграмма фазового состоянии смеси природного газа и природного газолина fill. 29].
Содержание жидкости, °/0 об
а —1 в координатах давление — содержание жидкости; Ь—в координатах давление — температур:).
Таблица III. 1
Состав природных углеводородных смесей
| Исследователи | ||||
| Эй- |
||||
| Компонент | Катц, | и | Вей- |
лертс и |
| Винк и | науг и | |||
| Давид |
фут | Бредли |
торы | |
Содержание, % мол.
|
Углекислый газ ..... . | — | — | 0,13 |
0,74 |
|
Азот........... | — |
— | 0,76 |
1,38 |
|
Метан.......... | 59,7 |
94,11 | 53,91 |
76,48 |
|
Этан........... | 8,9 |
2,67 | 14,20 |
7,92 |
| Пропан ......... | 5,0 |
0,89 | 9,64 |
4,30 |
|
Изобутан......... | 4,9 | 0,21 | 1,25 |
1,20 |
|
н-Бутан......... | 4,9 |
0,34 | 4,29 |
1,86 |
|
Изопентан........ | 9,3 | 0,20 | 1,12 |
0,94 |
| н-Пентан ......... | 9,3 |
0,10 | 1,87 |
0,78 |
| Гексаны ......... | — |
0,29 | 2,72 |
1,41 |
| Гексаны + высшие . . . . | 12,2 |
.— | — |
— |
| Гептаны + высшие .... | — |
1,19 | 10,11 |
2,99* |
| Молекулярный пес гептанов + высшие |
100,0 | 100,00 |
100,00 178,5 | 100,00 |
350
300
250 ^ 200 ^ /50 ^ 100
50
-80 -Ь-0 О ЬО 80 120 160 200
Температура,”С
Рис. 111.27. Диаграмма фазового состояния для природного газа [III. II].
Определенные смеси веществ имеют диаграммы фазового состояния, отличающиеся от типичных диаграмм такого рода. Например, эти смеси могут образовывать две жидкие фазы или могут иметь жидкости, выделяющие при испарении пары того же состава, что и жидкость, и поэтому выкипающие при постоянной температуре. Последние смеси описываются как азеотропные (минимум или максимум температуры кипения). Классическим примером этих смесей являются системы вода — углеводороды и вода — этиловый спирт.
Диаграммы, отличные от идеальных, образуют такие смеси, как этан — углекислый газ [III. 40] и ацетилен — этан или ацетилен — этилен [III. 43]. На рис III. 28 представлены данные фазового состояния системы этан — этилен—ацетилен при 4,5° С для трех бинарных смесей, две из которых являются азеотропными.
Нефть при ее деасфальтизации с помощью пропана разделяется на две жидкие фазы [I. 13]. Катц с соавторами [111.73] путем добавления пропана к системе природный газ — нефть получали две жидкие фазы. Боткин, Ример, Седж и Леси [III. 10] при исследовании фазового состояния двух калифорнийских нефтей получили несколько жидких фаз.
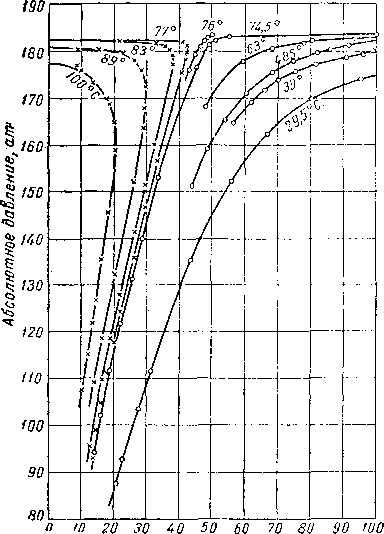
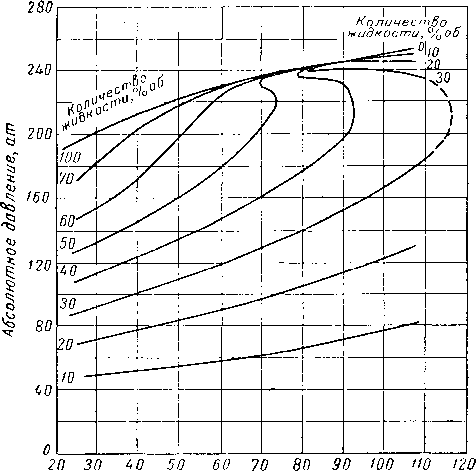
Вейнауг и Бредли (Weinayg and Bradley) [III. 75] наблюдали необычное фазовое поведение природной пластовой смеси (рис. III. 29). При постоянной температуре ниже критической и равной 71° С количество жидкой фазы сначала уменьшается, затем аномально увеличивается и после этого начинает нормально уменьшаться. Вейнауг и Бредли назвали это аномальное поведение системы возобновляющейся конденсацией или испарением. Состав этой системы (табл. III. I) характеризуется высоким содержанием пропана и этана. Аномальное поведение системы может быть, по-види-мому, объяснено намечающимся образованием второй жидкой фазы.
Эйлертс (Eilerts) с соавторами [III. 19] наблюдали образование второй жидкой фазы при —54° С для смеси, имеющей состав, показанный в табл. III. I. При этом смесь находилась при температуре ниже своей критической при давлениях 77—87 ат..
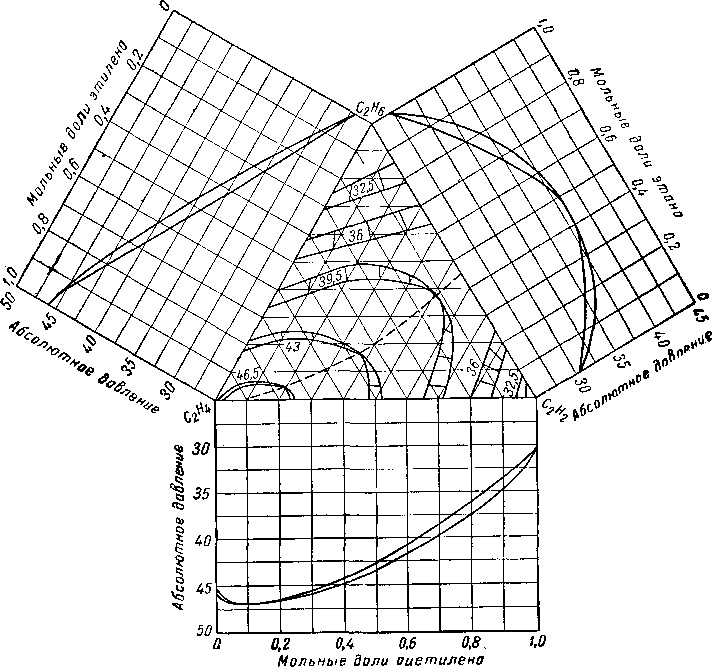
Рис. III. 28. Фазовое равновесие системы этан — этилен — ацетилен при 4,5° С
[III. 43].
Абсолютное давление в ат; цифры на кривых в ат.
1п / == In р —
(III. 7)
RT
(III. 2)
(III. 10)
¦ dp,
Рис. III. 29. Диаграмма фазового состояния, характерная для природной углеводородной смеси [III. 75].
§ 9. КОНСТАНТЫ РАВНОВЕСИЯ
Определение фазового состояния углеводородных смесей осуществляется с помощью констант равновесия системы жидкость — пар. Константа равновесия *=¦? х
где у — молярная доля компонента в паровой фазе; х — молярная доля этого же компонента в жидкой фазе, находящейся в равновесии с паровой фазой.
Константы равновесия соответствуют данному давлению и температуре. Во многих смесях при давлении, значительно меньшем критического, константы равновесия для большинства компонентов не зависят от состава фаз.
У
Очень важным является тот факт, что отношение ~
в довольно широком интервале изменения условий не зависит от состава смеси. Впервые константы равновесия были использованы для расчетов Брауном, Со-удерсом и их коллегами по Мичиганскому университету в 1937 г. [III. 67]. Льюис и Люк предложили метод применения летучести (фугетивности) для определения условий равновесия системы пар — жидкость [III. 41].
Для определения фазового состояния смесей веществ используются законы Рауля и Дальтона. Для данного компонента системы, находящейся в двухфазном состоянии при постоянных значениях температуры и давления:
уР — хр, (III. 3)
где Р — общее давление системы; р — давление насыщенного пара данного компонента.
Преобразование уравнения (III. 3) приводит к выражению этого закона через константу равновесия:
I = ? = (III. 4)
Закон Рауля имеет два недостатка: I) некоторые смеси веществ значительно отклоняются от этого за
T e м п e p a m уp a,°С
кона вследствие их химической природы; 2) этот закон применим для случая, когда температура смеси ниже значений критических температур всех входящих в нее компонентов; упругость паров смеси должна быть известна. Вследствие того, что критическая температура метана равна —82° С, закон Рауля очень редко может быть применен для природных газовых смесей, содержащих метан. Для смесей пропана, бутанов, пентанов и т. д. закон Рауля справедлив при температурах до 66° С и абсолютных давлениях до 7 ат.
Если в законе Рауля заменить давление на летучесть, то растворы могут быть рассмотрены как идеальные:
%fL ~ yfV’ (Ш- 5)
где 1ь — летучесть жидкого индивидуального компонента при равновесных значениях давления и температуры; fv—летучесть парообразного индивидуального компонента при равновесных значениях давления и температуры.
Идеальные константы равновесия были получены на основании равенства [III. 67]
У fr
К = ~=~. (III.6)
* fv
Было найдено, что летучесть можно определять экстраполированием и для области Температур, превышающих критические. Летучесть определяется из данных pVT по следующим термодинамическим формулам.
Определение летучести:
где z—коэффициент сжимаемости.
На рис. III. 30 приведена обобщенная диаграмма летучести природных газов, на которой даны значения коэффициента активности [III. 25], равного отношению f/р при различных значениях приведенных давлений и температур. Эти значения летучести могут быть использованы для определения идеальных констант равновесия [III. 67].
Если имеются значения констант равновесия, экспериментально определенные по составу паровой и жидкой фаз, то они могут быть использованы вместо идеальных констант равновесия. Работа Катца и Хегмута (Kalz and Hachrmith), опубликованная в 1937 г., была посвящена изучению констант равновесия для систем природный газ — нефть.
На рис. III. 31 приведено сравнение констант по закону Рауля с экспериментальными константами равнове-
где R— газовая постоянная; Т — абсолютная температура; V— удельный объем.
Это выражение равнозначно следующему равенству:
RTd (In /) == Vdp. (II!. 8)
При постоянной температуре, когда другие виды энергии, кроме тепла и компрессии, могут не приниматься в расчет, летучесть может определяться из выражения свободной энергии
dF = Vdp — RTd (In /). (III. 9,.
Выражение (III. 7) или (III. 8) может быть приведено к форме, удобной для расчета летучести жидких
и газообразных веществ, графическим методом:
*y-V)dp,
1п / = 1п р -
Р
• 1 — г
Р
сия. На этом графике представлены данные для системы природный газ — нефть при температуре 49° С, а также данные для бинарной системы метан — пропан, взятые из работы Седжа и Леси, и для системы этан — гептан,
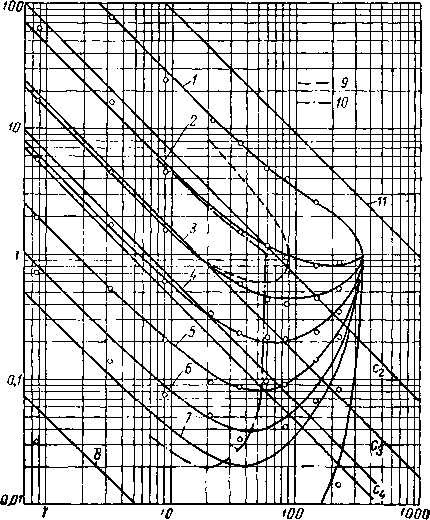
Абсолютное давление, am Рис, III. 31. Сравнение закона Рауля с экспериментально измеренными константами равновесия при 49° С [111.27].
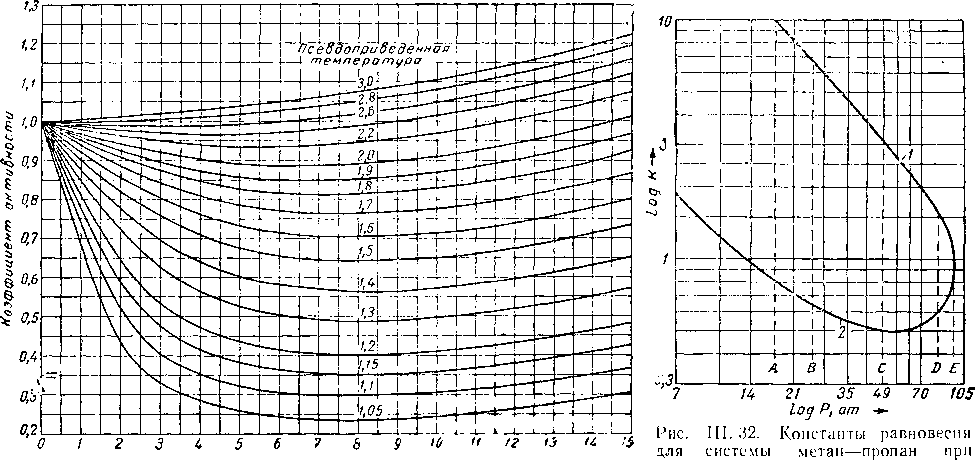
Рис. III. 30. Летучесть
Исевдоприведенное давление (фугетивность) природных газов [IV. 16,
383 С [III. 58].
1 — метан; 2 — пропан.
/ — метан; 2 —этан; 3 - пропан; 4 — бутаны; ,5 — пен-таны; 6 — гексаны; 7 — гептаны; 8 — гептаны +, 9 — по данным Седжа и Леси; 10 — по данным Кея; Ц закону Рауля.
<>Ч
III. 251. взятые у Кея. В
логарифмических координатах закон Рауля представляется прямыми линиями с коэффициентом пропорциональности, равным—1, и проходящими через значение давления, равного давлению насыщенного пара при принятой температуре. Для пропана и бутанов при давлениях ниже давления насыщенного пара экспериментальные константы равновесия отличаются от закона Рауля. При давлениях, превышающих давления насыщенного пара, экспериментальные константы равновесия сходятся в одной точке при К — I. Так, для пропана в метане при давлении 70 ат и температуре 49° С значение действительной константы равновесия равно 0,6, в то время как закон Рауля дает значение, равное 0,24. Подобный характер влияния давления подчеркивает, что константы равновесия изменяются в зависимости от состава фаз и значительно отклоняются от закона Рауля. Температура 49° С превышает критические температуры для метана и этана, поэтому проведенные для них линии на основании закона Рауля ненадежны при всех значениях давления.
Для лучшего понимания критических явлений и фазовых изменений можно пользоваться данными поведения бинарной системы. На рис, III. 32 приведена кривая констант 'равновесия для метана и пропана при 38° С. Эта кривая построена по данным исследования системы метан — пропан (см. графики на рис, III. 12, III. 16 и III. 17),
Для определения состава фаз тронных систем, помимо температуры и давления, требуется знать величину третьей переменной, в качестве которой может быть использован параметр, характеризующий состав смеси. Это позволит получить точки давлений сходимости, как показано на рис, III. 21 или III. 25.
До Настоящего времени исследовано большое число простых углеводородных систем, содержащих метан. Поэтому имеется достаточное количество данных для решения вопросов, связанных с такими системами. Многие вопросы, связанные с более сложными системами, могут быть решены с помощью изучения поведения бинарных и тройных систем. Данные для сложных систем и методы оценки их констант равновесия изложены в главе VI.
