Свойства нефтявых газовых коллекторов
Нефтяные и газовые коллекторы способны содержать в себе жидкости и газы и пропускать их сквозь себя. Жидкости и газы содержатся в порах и трещинах песчаников, доломитов, известняков, сланцев, мела и других пористых сред. Часть общего объема породы, представляемая пустотами, называется пористостью породы, Свойство лористой среды пропускать сквозь себя жидкости и газы называется проницаемостью. Из других свойств пористой среды следует указать на способность ее удерживать в состоянии капиллярного равновесия некоторое количество воды. Кроме того, следует указать на крайне сложную структуру порового пространства.
По существующим представлениям накопление нефти или газа происходит в пористой среде, предварительно заполненной водой. При этом нефть или газ не полностью вытесняют воду из лор пласта. Оставшаяся в пористой среде вода называется связанной. Знание пористости и доли порового объема, занятого связанной водой, необходимо для подсчета запасов нефти или газа и решения ряда вопросов проектирования, разработки и эксплуатации месторождений.
Пористость, проницаемость, нефтеводонасыщенность определяют обычно по образцам пористой среды, вырезанным из кернов, полученных при бурении скважин. Содержание связанной воды может быть также определено косвенным методом по кривым капиллярного давления. Некоторые свойства пород в зонах, прилегающих к скважинам, могут быть изучены с помощью электрокаротажа.
Многие породы, в частности песчаники, сложены из отдельных частичек, образующих жесткую структуру вследствие действия горного давления вышележащих пород, а также наличия между ними цементирующего материала. Размеры зерен песчаников большинства пористых сред колеблются в пределах 0,06—2 мм. Часто песчаники содержат некоторое количество более тонкозернистого материала, например глин, которые влияют на пористость и проницаемость этих пористых сред.
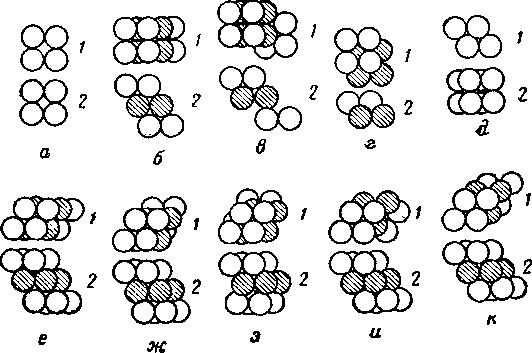
а_кубическая К* 1; 6 — орторомбическая К* 2 со сквозной порой; в — орто
ромбическая № 2 с закрытой порой; г — ромбоэдральная № 3; <Э^-орто ромбическая № 4; е — тетрагональная сфенондальняя № 5 со сквозной порой; ж _ тетрагональная сфеиондальная К* 5 с закрытой порой (/); з —тетраго нальная со сквозной порой; и — ромбоэдральная № б с открытой порой к — ромбоэдральная 6 с закрытой порой. У— вид сверху; 2 вид спереди.
Таблица II. 1 Коэффициенты пористости среды, представленной сферическими частицами различной укладки
Рис. II. 1. Типы упаковок сферических частиц одинакового диамет
| Вариант укладки |
Коэффициент пористости, доли единицы | Число точек кон-та кта, приходящихся на одну сферу |
Расстояние между слоями сфер |
| Кубическая . . . |
0,476 | 6 |
D* |
| Орторомби ческая | 0,3954 |
8 | 0,866 D |
| Ромбоэдральная . |
0,2595 | 12 |
0,707 D |
|
Орторомбическая . |
0,3954 | 8 |
D |
|
Тетрагональная | |||
| сфеноидальная . | 0,3019 | 10 |
0,866 D |
|
Ромбоэдральная . |
0,2595 | 12 |
0,816 D |
* D—диаметр сферических частиц. Данные взяты из [П. 49].
При изучении пористости зернистых материалов сначала определяют пористость сред, составленных из сферических частиц одинакового размера, уложенных различным образом. В табл. II. 1 и на рис. II. 1 показаны различные варианты укладки однородных сфер, имеющих пористость от 25,95 до 47,6%.
В реальных пористых средах частицы могут располагаться более компактно, чем это показано в табл. 11,1, даже при отсутствии цементирующего материала. Песчаник на выходах пласта Вилкокс (в горах Арбакл, в Оклахоме) имеет пористость 15% (проницаемость 400—900 мд). Этот носчаник не имеет цементирующего материала и рассыпается на отдельные зерна, после того как извлекается из обнажения.
Пористость образца, полученного после вторичной упаковки этого песка, равна 32,5—34%. Это указывает на то, что частицы в реальном песчанике уложены особым образом, в результате чего пористость может составлять 15%. Такая сравнительно низкая пористость песка, по-видимому, объясняется формой и размерами отдельных частиц, процессами их седиментации и действием горного давления.
О характере внутреннего строения нефтеоодержащих пористых сред можно примерно судить по внешнему виду кернов, отобранных при бурении скважин. На рис. II. 2 показан внешний вид кернов, отобранных из характерных нефтесодержащих отложений, а на рис. II. 3 представлены фотографии поверхности образцов доломитов Хьюготон, имеющих различные пористости [1.36].
Для исследования внутренней структуры кериов может быть применен следующий метод. Керны насыщаются каким-либо материалом с низкой температурой плавления (воском, пластмассой, металлическими сплавами и др.). Материал керна растворяется кислотами, а оставшийся наполнитель воспроизводит внутреннее пространство пористой среды. На рис. II. 4 показаны фотографии характерных пористых сред, обработанных подобным способом. На рис. II. 4, а показано поровое пространство образца известняка Арбакл, отобранного с глубины 1043,4—1044,6 м из скважины на промысле Силика в Канзасе. Пластмасса показана здесь черным цветом. Пустоты представляют собой объем, ранее занятый известняковым скелетом. Светлые оттенки, имеющиеся в большом количестве на фотографии, соответствуют (по данным анализа) гипсу и кварцу. Некоторые частицы этого материала покрыты слоем пластмассы, что завышает пористость, определяемую этим методом.
На рис. II. 4, в показан тот же известняк Арбакл. Объем, первоначально занятый известковистым материалом, растворен кислотой и представлен на фотографии темными участками. Паровое пространство этого образца имеет ячеистую структуру. Однако подобная обработка кернов не является удовлетворительной для известняка Арбакл.
Дело в том, что в образце, по-видимому, имеются в большом количестве нитевидные поры, которые при кислотной обработке кернов разрушаются.
На рис. II. 4, с представлено поровое пространство песка Вудбайн с месторождения Ист Техас. Светлая окраска на фото соответствует пластмассе и дает представление о структуре порового пространства керна. Черный цвет соответствует пустотам, образованным в результате обработки материала образца плавиковой кислотой. Из этого рисунка видно, что распределение пористости в песчанике более равномерное, чем в известняках, рассмотренных ранее. Данные анализа этого керна отсутствуют, тем не менее можно считать, что проницаемость его составила бы около 2100 мд, а пористость 25%.
На рис. II. 4, d изображена структура порового пространства керна из отложений Клирфорк промысла
Н. Монахенс в Западном Техасе. Белый цвет соответствует пластмассе, которой первоначально было заполнено поровое пространство керна. Темный цвет соответствует пустотам, первоначально занятым известковистым материалом. Отличительной чертой этого образца является «аличие леигочной (длинные извилистые поро-вые каналы) структуры порового пространства. Было обнаружено, что образцы такого типа имеют или очень низкую пористость, или вообще не имеют 'никакой эффективной пористости.
На рис. II. 4, е показана структура порового пространства девонского образца, отобранного из скважины промысла Фуллертон с глубины 2610 м. Эффективная пористость его 11,2%, а проницаемость 2890 мд. Детальное рассмотрение фотографии показывает, что высокое значение проницаемости образца является результатом высокой степени сообщаемостн его пор.

Рис. II. 2. Внешний вид кернов из скважин. й _ бартлесвилский песчаник, округ Кливленд, штат Оклахома с глубины 2242 м; b — девон, округ Ли. штат Нью-Мехико. с глубины 3707 м; с — ннжиий Фрио, округ Ньюекс. Техас, с глубины 2165 м; d — Елленбургер, округ Аптон Техас, с глубины 3965 м\ е — конгломерат Волфкамп. округ Крокет, с глубины 1847 м; f— иижний миоаеи, округ Керн. Калифорния, с глубины 5150 м.


Рис. II. 3. Доломит Хьюготон различной пористости (все фотографии выполнены в одном масштабе).
Данные анализа кернсв
|
1 | 2 |
3 | 4 |
5 | 6 | 7 | |
| Пористость, % . . . . |
0,49 | 7,27 | 9,67 | 10,25 | 13,29 |
16,6 | 23,6 |
|
Проницаемость, мд . Содержание связан | 0,073 | 0,025 | 0,645 | 1,17 v |
13,62 | 168,0 | 634,0 |
| ной воды, % . . . . |
85,0 | 64,0 | 17,8 |
28,5 | 25,4 | 11,4 | 12,8 |
8 — трещина постоянного размера; 9 — трещина переменного размера.


Рис. II. 4. Фотографии структуры порового пространства различных образцов. а и Ь— известняк Арбакл; с — песок Вудбайн; b извест-няк Клнрфорк; е — девонский известняк.


.Пористость экстрагированного сухого образца представляет собой отношение объема его пустот к объему всего образца (часто умножается на 100, чтобы получить значение пористости в процентах). При определении пористости следует различать два ее вида: эффективную пористость, равную отношению объема только открытых пор (без учета замкнутых пор) ко всему объему породы, и абсолютную пористость, определяемую отношением объема всех пустот (включая и замкнутые) к общему объему породы. Несоответствие значений этих видов пористости присуще известнякам или другим породам с большим количеством цемента, которые могут иметь пустоты, не сообщающиеся между собой. Как правило, разница значений этих видов пористости если и имеется, то очень незначительная.
Для определения пористости и проницаемости обычно применяются образцы Диаметром 20—25 мм и длиной 25—40 мм, получаемые из кернов, отобранных во время бурения скважин. Предварительно керны экстрагируются в аппарате Сокслета органическим -растворителем и высушиваются.
Общий объем образца пористой среды может быть определен по следующей методике: 1) взвешивание сухого керна; 2) насыщение керна под вакуумом жидкостью с известной плотностью; 3) взвешивание насыщенною керна.
Пористость подсчитывается по формуле
„ (объем пор)100
Пористость = -5- =
к объем кериа
_ (вес жидкости в порах керна) 100 ~ (плотность жидкости) х (объем керна)^ ^
Пример.
Вес сухого керна 19,810 г, вес керна, насыщенного тетрахлорэтаном, 22,413 г, вес жидкости в порах керна
2,603 г, платность жидкости рш = 1,600 г/см3. Общий объем керна 9,05 см3.
2,603 х 100
Пористость =
600 х 9,05
= 17,96%.
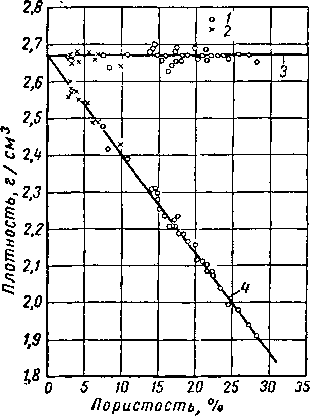
Рнс. II. 5. Плотность зерен породы и кернов в целом.
/ — песок: 2 — известняк; 3— плотность зерен породы; 4 — плотность керна в
По данным, получаемым по этому методу, опреде ляется объемный вес в целом, а также плотность зереи твердого тела, слагающего керн. На рис. II. 5 приведены типичные данные плотности кернов, отобранных из месторождений Оклахомы. Из этого ,рисунка видно, что плотность зерен пароды составляет 2,67 г/см3, а плотность кериа в целом в зависимости от величины пористости изменяется, принимая при пористости, равной нулю, значение, равное 2,67 г/см3. Этот график позволяет утверждать, что значения эффективной и абсолютной пористости для исследованных образцов практически одинаковы.
Эта методика определения пористости трудоемка, но при отсутствии специального оборудования может быть использована. Более предпочтительны экспресс-методы определения пористости, пригодные для массовых измерений. В настоящее время имеется большое количество методов исследования кернов [II. 4]. Наиболее простым методом определения пористости является метод, в котором объем твердого тела измеряется с помощью газа. Оригинальный метод определения пористости Уошберна—Бантиига неоднократно видоизменялся [II. 67, II. 5].
По методу Горного бюро (рис. II. 6) объем твердого тела определяется по разнице объемов воздуха в камере высокого давления при отсутствии и при наличии в ией керна. Объем бомбы и трубок между кранами С и 8 определяется заранее, а количество воздуха, содержащегося в этом объеме при определенном давлении (порядка 15 ат), измеряется с помощью газовой бюретки
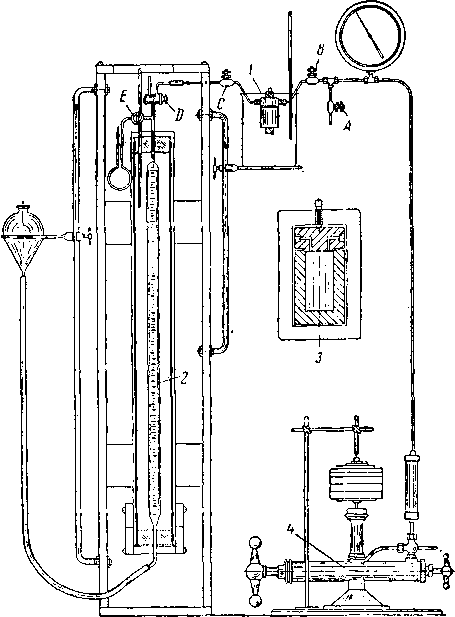
Рис. 11.6. Порозиметр Горного бюро [11.67].
/ — измерительная камера высокого давления; 2 — газовая бюретка; 3 — общий вид измерительной камеры; 4—* грузовой манометр.
при атмосферном давлении. Общий объем керна определяется с помощью ртутного пикнометра. Таким образом, пористость керна находится как отношение разницы общего объема керна и объема минерального скелета к общему объему керна.
В парозиметре Кобе (рис. II. 7) [II. 55, II. 5] объем минерального скелета керна и его общий объем определяются тем же самым прибором, что и в порозиметре Горного бюро. При этом общий объем керна определяется по разнице отсчетов шкалы микропресса с керном и без керна в 'измерительной камере. Определение проводится при атмосферном давлении.
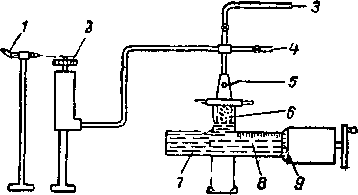
Рис. II.7. Порозиметр Кобе [П-55].
1 — окуляр; 2 — грузовой манометр; 3 — подвод газа; 4—сообщение с атмосферой; 5—смотровое окно; 6 — образец породы; 7 — ртутная емкость; 8 — поршенек; 9 — микрометрическая шкала мнкропресса.
Объем минерального скелета керна определяется посредством сжатия воздуха в измерительной камере ртутью от.атмосферного давления до некоторого давления, задаваемого прибором типа грузового манометра, с керлом и без керна в 'измерительной камере. Разность объемов ртути по шкале микропресса и значение объема газовой камеры при .нулевом отсчете микропресса позволяют рассчитать объем минерального скелета керна. Пористость подсчитывается аналогично предыдущему случаю.
В зависимости от природы применяемого газа значения пористости несколько изменяются. Это вызвано тем, что различные газы по-разному адсорбируются на твердой поверхности в зависимости от давления и температуры. Наиболее подходящим газом для этой цели является гелий, так как он не адсорбируется на твердой поверхности и имеет 'наименьшее отклонение от идеального газа.
Существует также метод определения пористости кернов, основанный на вдавливании ртути в поры керна. Этот метод сравнительно неточен, особенно для кернов низкой проницаемости, так как ртуть не полностью заполняет наиболее узкие поры керна при давлении 100 ат и более. Для этой цели применяются приборы, аналогичные изображенному на рис. II. 7. Перед заполнением керна ртутью он вакуумируется. После этого ртуть вводится в камеру до определенного уровня и отмечается показание микрометра. Далее над уровнем ртути создается давление газа и часть ртути входит в поры керна.
Уровень ртути с помощью микропресса снова приводится в первоначальное положение. По разности отсчетов я определяют объем ртути, вошедший в керн. Общин объем керна определяется по разнице показаний микропресса при наличии и отсутствии керна в измерительной камере.
В табл. II. 2 приведены результаты опытов Бурдайна, Гоурнея и Ричертса (Burdine, Gournay, Reichertz) [II. 15] по определению пористости кернов методом вдавливания ртути (при давлении 100 ат).
Объем порового пространства кернов, заполненных ртутью при давлении 100 am
|
№ керна |
Проницаемость по газу, мд |
Заполнение порового пространства ртутью, % | № керна | Проницаемость по газу, мд | Заполнение порового пространства ртутью, % |
|
171С | 17 |
76 | 190А |
93 | 80 |
|
164С | 86 |
69 | 174В |
36 | 71 |
|
171В | 2,6 |
85 | 173С |
20 | 78 |
|
261А | 0,5 |
56 | 311В |
52 | 68 |
|
174С | 38 |
75 | 192А |
1440 | 82 |
|
164В | 41 |
78 | 169В |
30 | 55 |
|
3I1A | 67 |
53 | 171Д |
22 | 85 |
|
I61B | 7 |
72 | 295А |
20 | 81 |
|
173Д | 16 |
77 | 261В |
0,01 | 60 |
|
163 А | 29 |
78 | 686 |
46 | 57 |
|
681 | 81 |
61 | 867 |
88 | 77 |
|
866 | 88 |
73 | 683 |
16 | 62 |
|
680 | 38 |
61 | 696 |
75 | 61 |
|
682 | 20 |
59 | 14564 |
112 | 80 |
|
826А | 140 |
85 | 13302 |
5 | 68 |
Примечание. Данные взяты нз [II. 15].
Данные, приведенные в этой таблице, показывают, что значения пористости, определенные этим методом, будут •занижены.
Метод определения пористости по плотности зерен, слагающих керн, состоит во взвешивании экстрагированного и высушенного керна и измерении его общего объема. Объем минерального скелета керна определяется делением веса керна на 2,67. Так как плотность различных минералов различна, то время от времени ее значение необходимо определять экспериментально.
В пяти лабораториях были проведены точные измерения пористости группы естественных и искусственных образцов [II. 22]. На рис. II. 8 представлены сравнительные результаты этих измерений для песчаника проницаемостью 20 мд.
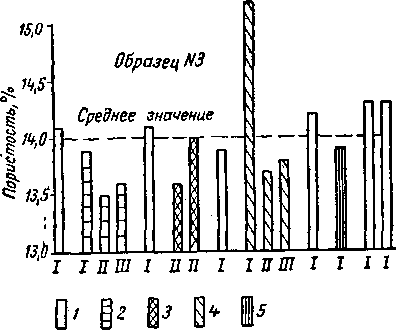
Рис. II. 8. Сравнение результатов измерений пористости, проведенных в пяти различных лабораториях [II. 22].
1. 2. 3, 4 и 5 — соответственно лаборатории А. В. С и Е. I — газ; 11 — вода; 111 — органическая ЖИД' кость
§ 3. ПРОНИЦАЕМОСТЬ И ЕЕ ИЗМЕРЕНИЕ
Проницаемостью называется -способность пористых сред пропускать через себя жидкости и газы. За единицу проницаемости принято дарси. Одна тысячная дарси — миллидарси.
Проницаемость К определяется из уравнения
К /—dp\ > { dL j ’
(II. 1)
1 — X 1 спз , сек 1 см
qu I— dL ~A
fir)-
К =
:дарси,
1 am
где q — объемная скорость в см3/сек; А — площадь поперечного сечения керна в см2; |х — вязкость жидкости —dp
(газа) в cri3-,-j?-—перепад давления на единицу длины
керна в ат/см\ К — проницаемость в д.
Керн с поперечным сечением в 1 см2 и длиной 1 см (рис. II. 9) имеет проницаемость, равную 1* д, если объемная скорость фильтрации воды (вязкость = 1 спз) составляет 1 см3/сек под действием Перепада давления, равного 1 ат.
Q ='
I.
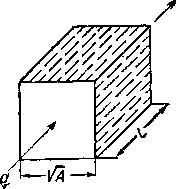
Рис. II. 9.
(II. 3)
-Р§).
(II. 4)
К :
[5],
Проницаемость измеряется путем пропускания жидкости или газа известной вязкости через образец с известными размерами и измерения объемной скорости фильтрации жидкости или газа и перепада давления, под действием которого происходит фильтрация (рис. II. 10). Керн вставляется в плотно подогнанную
(II. 5)
резиновую пробку так, чтобы не было зазора между пробкой и керном. Перепад давления измеряется по манометру, а скорость — диафрагменным расходомером или (когда скорость сравнительно мала) по скорости перемещения воздушного пузырька в калиброванной стеклянной трубке.
Уравнение (II. 1) написано в дифференциальной форме и для приведения к виду, удобному для вычисления проницаемости, должно быть проинтегрировано. В случае фильтрации жидкости объемная скорость постоянна, так как плотность ее во время движения по образцу практически не изменяется. Поэтому при движении жидкости в пористой среде, когда q, А, ц. и К постоянны, уравнение (II. 1) принимает вид:
Для газов объемная скорость q изменяется с изменением давления, и поэтому необходимо подставлять в уравнение (II. 2) значение q, соответствующее среднему давлению в образце, или при интегрировании уравнения (II. 1) следует учитывать, что объемная скорость q изменяется в зависимости от давления. Оба метода дают один и тот же окончательный результат, если газ подчиняется законам идеальных газов. Для перевода объема газа при среднем давлении в объем газа при атмосферном давлении применяют формулу
КА Pi — р2
Р1 ~Н Рг
2Рб
(II. 2)
Используя уравнение (11.2), получим
КЛ , 2
К
2L ц.рб 2QL ц. рб ' А{р\- р|)
2000 QL\i рб
К = . / о-— [мд\.
где К — проницаемость d мд; Q—объемная скорость газового потока в см3/сек; L — длина керна в см; р.— вязкость газа в спз; А — площадь поперечного сечения керна в см2\ рi —давление на входе в керн в ат; Pi — давление на выходе из керна в ат; рб— барометрическое давление в ат.
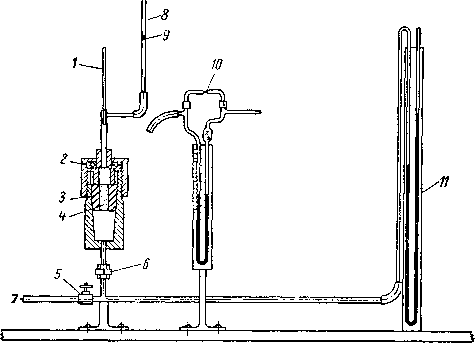
/ — термометр; 2 — шарикоподшипник; 3 — резиновая пробка; 4 — образец породы; 5 — игольчатый вентиль: 6«— соединительная муфта; 7 — вход воздуха; 8—градуированная труб* ка; .9 — вода; 10 — реометр; // — манометр.
В табл. II. 3 приведены данные расчета проницаемости песчаного керна с пористостью 18,2%. Чтобы доказать, что значение проницаемости не зависит от скорости фильтрации, определяли ее при четырех различных скоростях фильтрации.
Если бы 'скорость фильтрации стала слишком большой, то проницаемость уменьшилась бы при расчетах по приведенным выше формулам, так как в этом случае движение газа в образце перестало бы подчиняться закону Дарси.
Существует несколько приборов для определения проницаемости кернов с минимальными затратами вре мени на измерения и расчеты (рис. II. 11).
Проницаемость естественных кернов следует измерять как в направлении напластования, так и перпендикулярно этому направлению, для чего образцы соответствующим образом вырезаются из кернов (см. рис. II. 2, а). Если пласт содержит глинистые прослойки, то проницаемость В перпендикулярном напластованию направлении
Рис. II. 10. Измерение проницаемости.
рическое давление 763 мм рт. ст., температура 20°С, jx]
возд '
0,0181 спз.
|
№ опыта | Pi. мм рт. ст. | Скорость течения воздуха | Перепад давления | (pjf-pf) X X 10—3 | К, мд | ||||
| диа фрагма | перепад давления на диафрагме, мм вод. ст. | Q, см*/сек | Рг. мм рт. ст. изб. | Рг, мм рт. ст. абс. | Pimm рт. ст. абс. | ||||
| 1 | 782 | А | 17 |
0,88 | 1,2 |
764 | 1545 |
1805 | 9,36 |
| 2 | 729 |
А | 15 |
0,80 | 1,1 |
764 | 1492 |
1642 | 9,35 |
| 3 | 276 |
В | 87 |
0,24 | 6,25 |
769 | 1039 |
488 | 9,44 |
| 4 | 180 |
В | 54 |
0,15 | 3,95 |
767 | 943 |
301 | 9,57 |
К = С-
где С =
2П00^р2атРб
2000 X 2,36 X 0,0181 X 760* 763
Л рат 2,58
Pi и рг даны в абсолютных мм рт. ст.
760
= 19,20 X 10е;
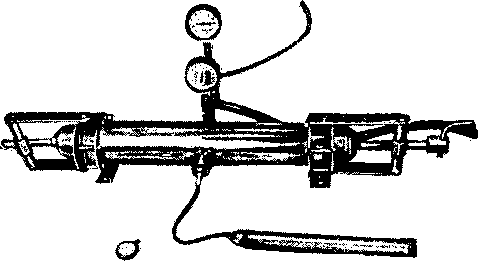
Рис. 11.12. Общий вид прибора Хасслера для измерения проницаемости цельных естественных кернов [11.43].
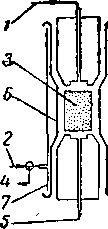
Рис. II. 11. Прибор для определения проницаемости кернов по газу.

J
в
будет меньше, чем проницаемость в направлении напластования. Характерные данные приведены в табл. 11.4.
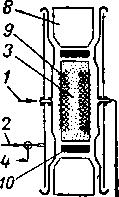
В естественных кернах известняка или доломита (см. рис. 11.2,6) пористость может быть в виде каверн или пустот растворения, которые могут не попасть в образец. В этом случае необходимо определять пористость и проницаемость для всего отобранного керна. На рис. 11. 12 и 11. 13 [11.43] показан прибор для измерения проницаемости таких естественных кернов (то типу прибора Хаослера).
Рис. 11. 13. Схематическое изображение кернодержателя прибора Хасслера [11.43].
а — измерение проницаемости в вертикальном направлении ; Ь — измерение проиица-емости в горизонтальном положении. I — воздух низкого давления (для создания потока); 2 — воздух высокого давления (для аэрообжима); 5*— керн; 4 — вакуум; 5 —к расходомеру; 6 — резиновая трубка; 7 — труба; 8 — металлическая пробка; 9 — сетка; 10 — резиновый диск.
| Объект исследования | Пористо сть, % |
Прони цае мость. мд |
| Бартлесвиллскин песчаник (Оклахома) | 14.7 19,4 17,3 15.8 12.9 |
6,7 48,7 41.5 18,2 21.5 |
| Песчаник Бенойст (Иллинойс) | 16,7 14.2 15.3 12,5 15,1 |
87,5 15,7 58.0 20.0 323 |
| Песчаник Кромвелл (Оклахома) |
13,9 14.2 16.3 10,8 |
171 174 366 51 |
| Песчаник Кипресс (Иллинойс) | 13,7 16,4 20 | 30 249 74 |
|
Еленбергер, доломит (Техас) |
5,4 | 1285 |
| Песчаник Фрио (Техас) |
22,4 18,1 25,1 |
1475 42,2 860 |
| Песчаник Катчелл (Калифорния) | 13,9 14,1 |
965 425 |
|
Песчаник Гленн (Оклахома) |
16,6 16.3 17.3 20 |
9,5 10 105 302 |
| Песчаник миоцена (Луизиана) | 36.1 33.2 39,4 37.3 37,8 34.2 32.2 | 578 1455 745 810 360 980 1040 |
Песчаник Тенслип (Вайоминг)
Песчаник Вилкокс (Оклахома)
Вилкокс
Песчаник Вудбайн (Техас)
Брендфордский песчаник
Примечание. Данные взяты из [II. 35. II. 26, 11.41].
|
Порис тость, % |
Прони цае мость, мд |
| 28,0 |
14,3 |
| 30,5 |
207 |
| 30,2 | 328 |
|
30,2 | 220 |
| 33,9 | 470 |
| 33,6 | 595 |
| 28,9 | 344 |
| 24,9 |
261 |
| 11,8 |
86 |
| 18,0 |
53 |
| 14,0 | 189 |
|
12,9 | 119 |
| 11,3 | 128 |
| 9,3 | 9,7 |
| 19,1 | 99,5 |
| 21,2 | 67 |
| 22,1 |
84 |
| 25,6 |
119 |
| 19,8 |
242 |
| 23,6 | 1650 |
|
23,7 | 2150 |
| 13,1 | 356 |
| 19,2 | 456 |
| 18,1 | 155 |
| 16,9 |
388 |
| 13,4 |
67 |
| 21,9 |
1030 |
| 19,1 | 780 |
|
15,2 | 560 |
| 26,8 | 2110 |
| 25,3 | 276 |
| 23,8 | 111 |
| 22,1 |
3390 |
| 27,7 |
859 |
| 29,0 | 341 |
|
10,4 | 0,77 |
| 12,6 | 1,67 |
| 14,8 | 16,8 |
| 14,2 | 2,7 |
| 16,7 |
55,8 |
Объект исследования
Оолитовый песчаник Родесса (Луизиана)
Песчаник Лос-Анжелос III (Калифорния)
Присутствие глинистого материала в кернах вызывает осложнения при измерении проницаемости. При сушке такого керна глина (особенно бентонитовая) может сократиться в объеме и воздухопраницаемость высушенного керна будет большей, чем могла бы быть проницаемость его по воде. Следует учитывать также, что в пресной воде глины набухают больше, чем в соленой. Поэтому применение пресной воды для измерения проницаемости глинистых кернов может привести к заниженным значениям проницаемости. В табл. II. 5 приведены данные Джонстона и Бисона (Johnston and Beeson) [II. 39] по измерению проницаемости калифорнийских кернов, содержащих глилу.
Обычно проницаемость измеряется при фильтрации через кери воздуха. В связи с этим целесообразно рассмотреть изменение свойств газов в процессе фильтрации их три иизких давлениях в капиллярах малых размеров. Если размер капилляра соизмерим со средней длиной свободного пробега молекул, то газ. движется в этом капилляре быстрее, чем это должно следовать из закона Пуазейля и Дар-си. Теория ламинарного движения предполагает, что скорость движения на стейке твердого тела равна нулю и в слоях движущегося газа имеется напряжение сдвига.
Проницаемость естественных кернов по воздуху, пресной и соленой воде
| Проницаемость, мд | Отношение проницаемостей по пресной н соленой воде, % |
Про-иицаемость, мд |
Отношение проницаемостей по пресной н соленой воде, % |
Проницаемость, мд |
Отношение проницаемостей по пресной и соленой воде, % |
Проницаемость, мд |
Отношение проницаемостей по пресной н соленой воде, % |
||||||||
| по возду ху | по соле ной воде |
по прес ной воде | по возду ху |
по соле ной воде | по прес ной воде |
по воз духу | по соле ной воде |
по прес ной воде | по возду ху |
по соле ной воде | по прес ной воде |
||||
| Скважина А Сцементированная порода | Скважина Б Рыхлая порода | Скважина В Сцементированная порода | Скважина Г Рыхлая порода | ||||||||||||
| 285 |
62 | 2,2 |
3,6 | 660 |
354 | 17 |
4,8 | 368 |
41 | 27 |
66 | 350 |
165 | 115 |
70 |
| 481 |
228 | 11,0 |
4,8 | 655 |
340 | 26 |
7,6 | 445 |
70 | 62 |
89 | 455 |
110 | 105 |
95 |
| 123 |
82 | 5,9 |
7,2 | 680 |
342 | 38 |
11 | 221 |
28 | 8,3 |
29 | 625 |
85 | 25 |
29 |
| 113 |
43 | 1,9 |
4,4 | 296 |
198 | 40 |
20 | 302 |
58 | 54 |
93 | 975 |
540 | 36 |
6,7 |
| 61 |
6,8 | 1,2 |
18 | 374 |
279 | 63 |
23 | 73 |
2,5 | 0,8 |
32 | 1550 |
1140 | 200 |
18 |
| 36 |
0,4 | 0,1 |
25 | 1030 |
485 | 22 |
4,5 | 33 |
4,5 | 5,0 |
111 | 565 |
505 | 210 |
42 |
| 159 |
1.6 | 0,4 |
25 | 192 |
98 | 21 |
22 | 266 |
69 | 50 |
72 | 6890 |
5510 | 330 |
6,0 |
| 72 |
2,3 | 0,7 |
30 | 2111 |
65 | 48 |
74 | 616 |
230 | 168 |
73 | 5000 |
2980 | 155 |
5*2 |
| 310 |
5,0 | 1,5 |
30 | 625* |
242 | 170 |
70 | 262 |
25 | 35 |
140 | 875 |
495 | 28 |
5,7 |
| 328 |
57 | 51,0 |
90 | 420 |
216 | 22 |
10 | 191 |
57 | 50 |
88 | 420 |
415 | 101 |
24 |
| 42 |
23 | 6,4 |
28 | 236 |
112 | 17 |
15 | 283 |
41 | 42 |
102 | 4250 |
2510 | 34 |
1,4 |
| 24 |
24 | 16,0 |
67 | 260 |
129 | 56 |
43 | 130 |
34 | 33 |
97 | 3510 |
2160 | 84 |
3,4 |
| 51 |
16 | 5,6 |
35 | 322 |
168 | 29 |
17 | 304 |
21 | 15 |
72 | 3140 |
2100 | 40 | I 9 |
| 42 |
29 | 4,1 |
14 | 330 |
58 | 8 |
14 | 66 |
32 | 20 |
63 | 3120 |
1950 | 150 |
I 7,7 |
|
35 | 17 |
2,7 | 16 |
560 | 240 |
56 | 23 |
61 | 17 |
15 | 89 |
1120 | 540 |
135 | 25* |
|
41 | 15 |
5,1 | 34 |
214 | 63 |
7 | 11 |
10 | 3 |
4 | 133 |
1870 | 1090 |
355 | 33 |
|
22 | 14 |
4,0 | 29 |
715 | 437 |
15 | 3,4 |
52 | 20 |
20 | 100 |
3810 | 3410 |
1170 | 34 |
|
46 | 16 |
5,7 | 35 |
470 | 305 |
27 | 8,8 |
50 | 22 |
5,4 | 25 |
1530 | 875 |
125 | 14 |
| 92 | 89 |
12,0 | 13 |
535 | 267 |
11 | 4,1 |
117 | 37 |
26 | 70 | ||||
| 178 |
40 | 6,4 |
16 | 405 |
217 | 14 |
6,4 | 230 |
134 | 70 |
52 | ||||
| 20 | 12 |
2,9 | 24 |
325 | 186 |
14 | 7,5 |
14 | 9 |
5 | 55 | ||||
| 14 |
5,9 | 1,8 |
31 | 270 |
101 | 34 |
34 | ||||||||
|
9,8 | 6,1 |
2,8 | 46 |
470 | 240 |
59 | 25 | ||||||||
| 25 |
13 | 3,5 |
27 | ||||||||||||
| 14 |
9,9 | 3,5 |
35 | ||||||||||||
| 36 |
22 | 3,5 |
16 | ||||||||||||
| 104 |
6,7 | 2,1 |
31 | ||||||||||||
| 88 |
11 | 2,3 |
21 | ||||||||||||
| 438 |
360 | 4,9 |
1,4 |
. | |||||||||||
* Сцементированные образцы. Данные взяты из (11.39).
§ 4. ЯВЛЕНИЕ ПРОСКАЛЬЗЫВАНИЯ ГАЗА
Используя в качестве модели стеклянный капилляр, Клинкеиберг (KHnkenberg) [II. 44] вывел уравнение, связывающее проницаемость по газу с проницаемостью по жидкости (или газу высокого давления), средняя длина свободного пробега молекул которой экспериментально мала: где Кг — проницаемость по газу; Кш—проницаемость по жидкости или, по газу высокой плотности; А —средняя длина свободного пробега молекул газа при давлении, при котором измеряется проницаемость; с — коэффициент пропорциональности, приблизительно равный единице; г — радиус капилляра.
Так как средняя длина свободного пробега молекул для идеальных газов обратно пропорциональна давлению, а значение г соответствует определенной пористой сре>-е,
где Ь —коэффициент, постоянный для данной системы газ — твердое тело; рср—среднее давление газа, фильтрующегося через пористую среду.
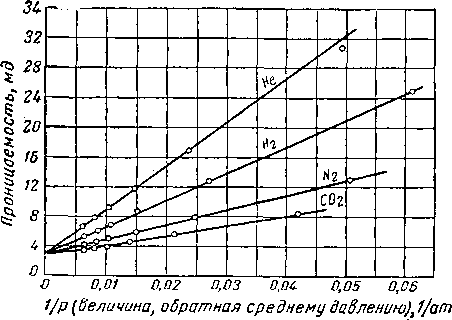
Отсюда следует, что проницаемость по газу обратно пропорциональна давлению газа. Поэтому зависимость проницаемости образца по газу от величины, обратной давлению газа, является прямолинейной. На рис. II. 14
| т,Б6 |
20 W 60 80
О
<ъ 300 s
f
*200
<Ъ
I»
J-(величин а ^обратная среднему Р давлению), 1/ат
Рис. II. 14. Проницаемость образца по воздуху при различных давлениях [II. 44]. Проницаемость образца по жидкости разна 23,66 мд.
представлена подобная зависимость, полученная Клин-кенбергом для образца, имеющего проницаемость по жидкости, равную 23,66 мд. Этот график показывает, что давление газа влияет на величину проницаемости, а также доказывает справедливость положения о том, что эффект проскальзывания имеет место ib случае малой разницы между средней длиной свободного пробега молекул и диаметром поры. Необходимо отметить, что все точки на рис. II. 14 соответствуют давлению 1 ат, т. е. условия определения проницаемости были в данном случае необычными. Результаты этих опытов приведены также в табл. II. 6.
Таблица //. 6
Значения проницаемости керна по воздуху при различных значениях давления
(проницаемость по жидкости 23,66 мд)
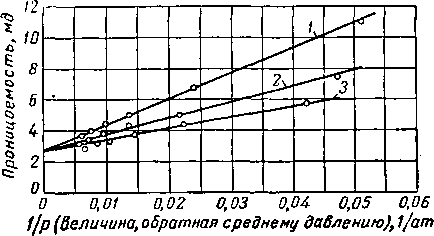
Рис. II 15. Влияние давления на проницаемость пористой среды для различных газов [II. 17] при температуре 25° С.
| Среднее давление, am |
Величина, обратная давлению, 1 /ат | Проницаемое гь, мд | Среднее давление, ат |
Величина, обратная давлению, 1 /ат | Проницае мость, мд |
|
0,01036 | 96,56 |
290 | 1,57 |
0,636 | 26,79 |
| 0,01633 | 61,20 |
197 | 2,657 |
0,3764 | 25,22 |
| 0,05921 | 16.89 |
75,6 | 5,10 |
0,1961 | 24,62 |
| 0,1464 | 6,829 |
46,6 | 9,19 |
0,1088 | 23,93 |
| 0,799 | 1,251 |
28,6 | 20,01 |
0,0499 | 23,65 |
Примечание. Данные взяты из [II. 44].
Калхаун и Юстер (Calhoun and luster) [II. 17] исследовали эффект проскальзывания для различных газов, включая метан, этан и пропан (рис. II. 15 и II. 16). В качестве пористой среды они использовали фильтр из стекла лирекс с проницаемостью по керосину 2,70 мд. Экстраполированное значение проницаемости этого фильтра по различным газам составило (рис. II. 15 И II. 16) 2,75 мд.
Так как данные проницаемости используются в процессах, происходящих в условиях, отличных от тех, при которых она измеряется, желательно иметь значения проницаемости для жидкостей и газов при давлениях, близких к пластовым При повышении давления длина
Рис. II. 16. Влияние давления на проницаемость пористой среды для метана, этана и пропана [II. 17] при температуре 25° С.
/ — метан; 2 — этан; 3 — пропан.
свободного пробега молекул газа уменьшается. Поэтому расход газа через пористую среду будет меньше расхода, который должен получаться соответственно проницаемости, измеренной при атмосферном давлении, так как эффект проскальзывания газа уменьшается с увеличением его давления. Следует помнить, что при низких давлениях эффективная проницаемость пористой среды для газов из-за явления проскальзывания больше, чем проницаемость ее для жидкостей.
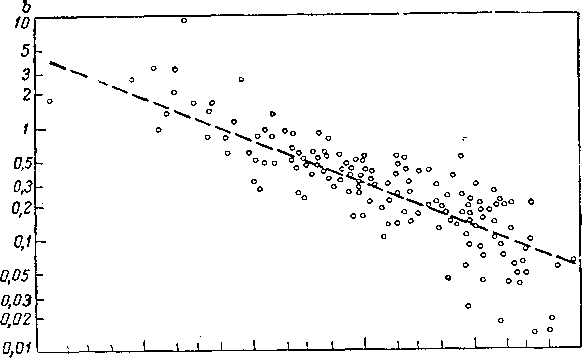
Юотер с сотрудниками [II. 35] исследовали явление проскальзывания для ряда кернов, охарактеризованных значениями пористости и проницаемости по воздуху и по керосину. На рис, II. 17 представлены результаты их опытов в виде зависимости постоянной Ь из уравнения (II. 7) от проницаемости кернов по жидкости. На основании этих экспериментов ими дана эмпирическая зависимость
h = 0.77 К~0'39. (П. 8)
Обычно проницаемость по воздуху измеряется при среднем давлении, несколько большем 1 ат. Используя значения Ь из рис. II. 17 и значение среднего давления Рср(1; 1,5; 2,0; 2,5 и 3 ат), при котором происходит течение воздуха через керн, находим величину поправочного коэффициента. При умножении этого коэффициента на величину проницаемости по воздуху получаем значе-
Рис. II. 17. Зависимость коэффициента Ь от проницаемости кернов
по жидкости.
0,010,02 0,05 0,1 0,2 0,5 1,0 2 5 10 20 50 100 200 50010U0
Проницаемость Кж,мд
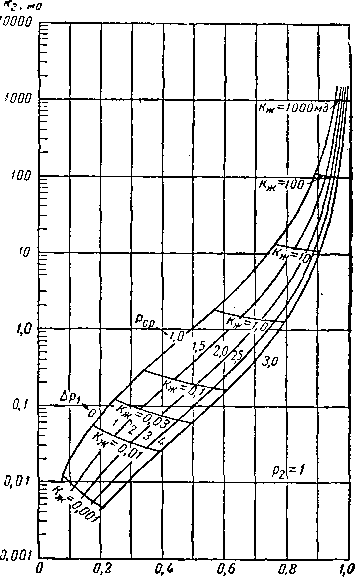
Поправочный коэффициент т = — кг
иие проницаемости для жидкости или проницаемости для газа .при высоком давлении, что иллюстрируется графиком рис. 11.18. Например, при Лш = 0,1 мд из рис. II. 17 коэффициент Ь = 1,91 При давлении, равном
1 ат, имеем
m = у—
г
Проницаемость по газу из рис. II. 18 Лг = 0,291, а проницаемость по жидкости Кж = 0,343 X 0,291 = 0,1 мд. Кривые на рис. II. 18 соответствуют перепадам давления на концах керна Д р, равным 0, 1, 2, 3, 4 ат для случая давления на выходе из керна, равного I ат. Большой разброс точек на графике рис. II. 17 показывает, что сопоставление кернов по проницаемости недостаточно точное. Наиболее целесообразно для этих целей использовать средний диаметр пор, полученный по измерениям капиллярного давления. К сожалению, определение кривых капиллярного давления не входит в обычную методику анализа кернов. Для оценки эффекта проскальзывания газа по измерениям проницаемости, особенно для кернов с низкими значениями проницаемости, определение проницаемости желательно проводить при двух как можно меньших значениях среднего давления. При отсутствии таких данных средний поправочный коэффициент может быть получен из рис. II. 18. Следует, однако, помнить, что действительное значение поправочного коэффициента для конкретных пористых сред может отличаться от этого среднего значения, что подтверждается большим разбросом точек на рис. II. 17.
Значения коэффициента Ь могут быть использованы для вычисления эффективной проницаемости по воздуху
Рис. II. 18. Поправка к воздухопроницаемости на эффект проскальзывания.
¦и при других значениях среднего давления. При определении проницаемости кернов не по воздуху, а по другим газам значение коэффициента Ь для этого газа может быть найцено из соотношения
А 1
(II. 9)
^газ ^газ
где ^ —средняя длина свободного пробега молекул.
Средние длины свободного пробега молекул воздуха и других газов должны браться при одном и том же давлении.
Явление проскальзывания прежде называлось киу-диновским или молекулярным течением. В известном смысле газ частично диффундирует через пористую среду. При меньших давлениях газ диффундирует на большее расстояние, чем при высоких, и тем самым способствует общему течению газа через пористую среду. Явление проскальзывания в условиях неустановившегося течения газа изучалось Валлиском и Ароновским (Wallisk and Aronofsky) [II. 69].
§ 5. ТУРБУЛЕНТНОЕ ТЕЧЕНИЕ2
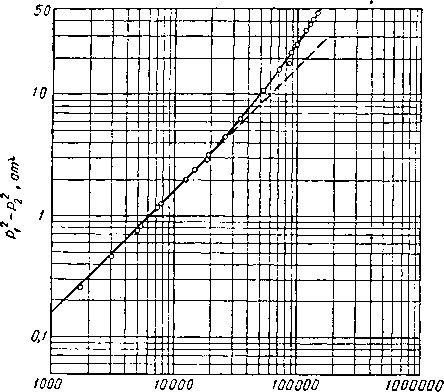
При течении жидкости в пористой среде обычно скорость потока прямо пропорциональна перепаду давления. Начиная с некоторого значения, увеличение скорости перестает соответствовать увеличению перепада давления для жидкости (или разницы квадратов давлений для газа) (рис. II. 19). Это явление было обнаружено Осборном Рейнольдсом в 1901 г. при исследовании течения жидкостей в трубах. Он проводил свои классические эксперименты на стеклянных трубках. В поток воды, движущейся по трубкам, добавлялось красящее вещество. В результате этих опытов было установлено,
V, см/сек
Рис. II. 19. Зависимость скорости от перепада давления при движении воздуха через песчаник Вилкокс [11.20] при t= 15,5°С и р=1 ат.
что струйное течение воды имеет место до тех пор, пока скорость течения прямо пропорциональна перепаду давления. Начиная с момента, когда пропорциональность зависимости скорости течения от перепада давления нарушается, Рейнольдс заметил турбулизацию потока. К такому режиму, когда скорость течения жидкости в трубах пропорциональна перепаду давления, обычно применяются термины струйное, ламинарное или вязкостное течение. Турбулентным называют течение, при котором нарушается эта пропорциональность и когда при течении жидкости в трубе начинает наблюдаться турбулизация потока.

Рис. II. 20. Течение через суженную часть порового канала.
а — ламинарное течение; Ь — переходное течение; с — турбулентное течение.
Фенчер и Льюис (Fancher and Lewis) [11.26] представили данные по течению жидкостей в пористой среде ¦и установили ту же терминологию ламинарного и турбулентного течения. Их данные приведены на рис. 11.21 в виде зависимости коэффициента трения от числа Рейнольдса. Отклонение этой зависимости от «прямолинейной (соответствующей наклону 45°) при высоких значениях скорости течения означает начало турбулизации потока.
При течении жидкостей и газов в пористых средах турбулизация потока наступает раньше, чем при течении в трубах. Однако для сцементированных пористых сред с очень малыми размерами пор и низкими значениями проницаемости трудно визуально наблюдать завихрения или турбулизацию в каналах пористой среды, хотя для такой среды существуют те же соотношения между перепадом давления и скоростью течения. Предлагаются различные объяснения поведения потока при высокоскоростных режимах течения [II. 3, 11.30].
Аномально высокий перепад давления обусловлен инерционными силами, проявляющимися в жидкости, фильтрующейся по узким каналам. В условиях ламинарного течения (рис. II. 20, а) кинетическая энергия жидкости и энергия давления при движении ее из / в
2 и далее в 3 взаимно переходят друг в друга. При высоких скоростях движения (рис. II. 20, с) превращение кинетической энергии в энергию давления при движении из 2 в 3 происходит не полностью, при этом кинетическая. энергия частично затрачивается на вихревое движение жидкости. Эта потеря энергии вызывает (за счет инерционных сил) повышенное падение давления на частице твердого тела в 2. Некоторые авторы применяют термин «турбулентность» к совершенно беспорядочному течению жидкости во времени в данной точке. По этому определению течение жидкости на рис. 11.20, с не может быть названо турбулентным. Если имеет место аномальное течение жидкости, на которое затрачивается повышенная потеря давления, то в этом случае применение термина «турбулентное течение» можно считать справедливым. Промежуточный случай (рнс. 11.20, Ь) соответствует состоянию, при котором увеличение скорости приводит к удлинению плоскости сдвига между слоями без образования вихревого движения, требующего добавочного расхода энергии. В настоящее время общепринято применять термин «турбулентное течение» к таким условиям, при которых зависимость скорости течения жидкости от перепада давления перестает быть линейной (а в случае течения газа не удовлетворяется линейная зависимость старости от разности квадратов давлений на концах керна).
Уравнение Дарси [II. I], справедливое для ламинарного течения, не может быть использовано для описания турбулентного течения. Форшеймером (Forscheimer) было предложено двучленное уравнение, связывающее перепад давления со скоростью течения, справедливое как для ламинарного, так и для турбулентного течения:
где р — давление в ат; L — длина в см; (J- —вязкость в спз; v—скорость в см/сек; К — проницаемость в д; р —плотность в г/см3; Р—коэффициент турбулентности в ат ¦ сек2/г.
Для газов это уравнение лучше выражать через мас-W
совую скорость —= ру, так как для одного и того же А
сечения потока газа его массовая скорость постоянна, что позволяет интегрировать это уравнение. Здесь W—массовая скорость движения в г/сек; А — площадь поперечного сечения потока в см2:
рТГ-?Г + Рр’"’=ы+ p(j)!-
Так как
Мр
то
1 1
где М — молекулярный вес; г ¦— коэффициент сжимаемости; R — газовая постоянная; Т — абсолютная температура.
1 — нефть,
И — вода,
(по данным Фенчера — Льюнса);
площадь поперечного сечения
10*10
10*10
10x10
ют
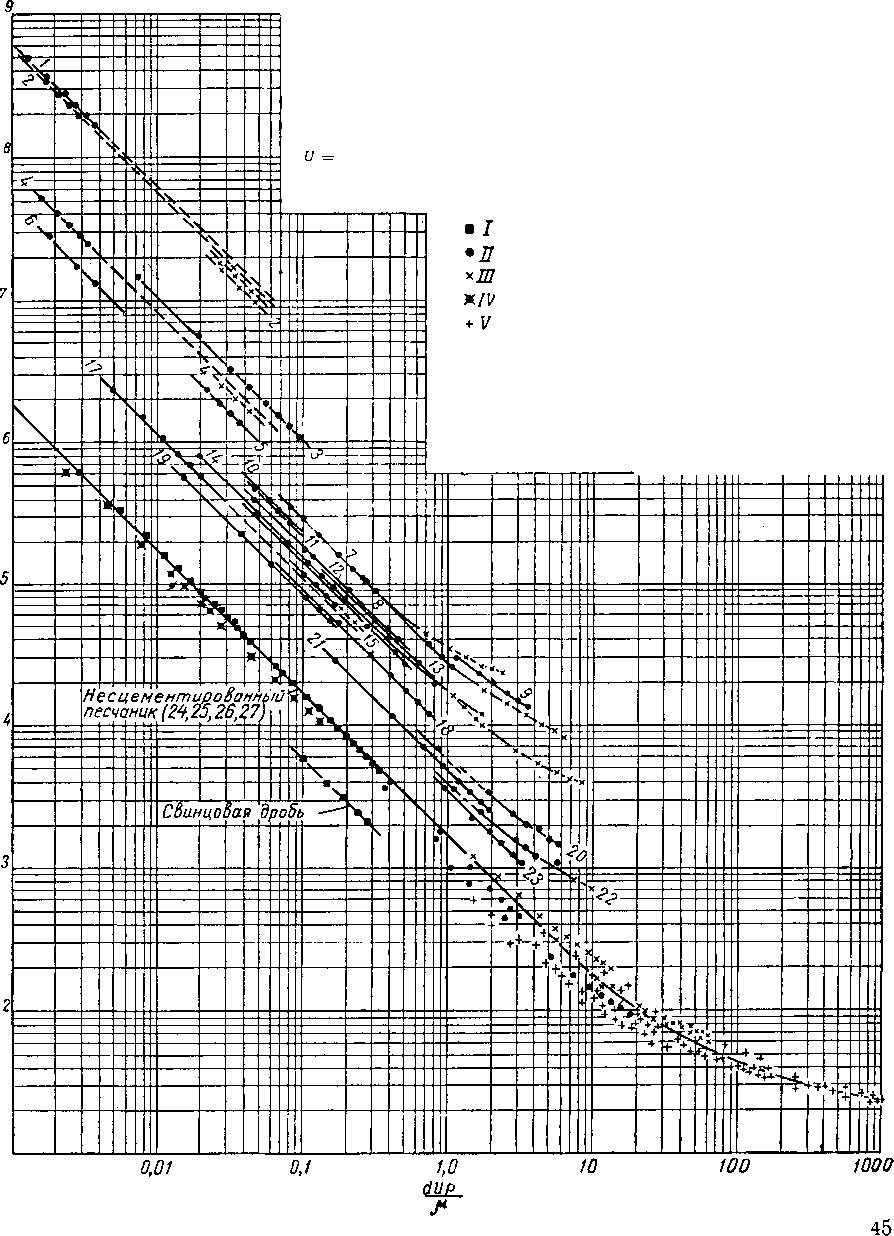
III — воздух IV — нефть (по данным Клоуда); V — газ (по данным Горного бюро)./—коэффициент сопротивления, безразмерный; g “ 981 см/сек2\ d — средний диаметр зереи в см; Д Р — перепад давления в кГ!см2; I — длина образцов в см р — плотность жидкости или газа в Г/слЗ; |i — вязкость в г/см • сек; V — скорость фильтрации;
_объемная скорость
W'W
10*10
| 'З: | N |
| ъ | |
| CSj | |
| II |
|
| ч* | |
10*10
10*10
| Лй образ ца | Песчаник | Пори стость, % |
|
Сцементн рооанные | ||
| / | Бредфордский | 12,5 |
| 2 |
Бредфордский | 12,3 |
| 3 | 3-й Венанго . . . | 16,9 |
| 4 | Керамика А . . . | 37,0 |
| 5 | Робинзон .... | 20,3 |
|
6 | Керамика В . . . |
37,8 |
| 7 |
Вудбайн . .... | 19,7 |
| 8 | Вилкокс..... |
15,9 |
| 9 |
3-й Венанго . . . | 11,9 |
| 10 | Робинзон ..... | 19,5 |
| 11 | Робинзон . • | 18,4 |
| 12 | 3-й венанго . . | 22,3 |
|
13 | Вилкокс ..... |
16,3 |
| 14 | 19,2 | |
| 15 |
3-й Венанго . . | 21,4 |
| 16 | Робинзон .... | 20,6 |
| 17 | Керамика С . . . | 33.2 |
| 18 | 3-й Венанго . . . | 21,9 |
| 19 | Вудбайн ..... |
23,8 |
| 20 |
Вудбайн .... | 26,9 |
| 21 | Вудбайн ..... |
27,7 |
| 22 |
Вудбайн..... | 22,1 |
| 23 | Вудбайн ..... |
28.8 |
| Нес | цементированные | |
|
24 | Флнит ..... |
38,5 |
| 25 |
Оттава ...... | 30.9 |
| 20 | 90—30 Оттава . . |
34,5 |
| 27 |
Лед тот ... | 34,5 |
''is
*
Ч;
г., О О
3.00
гЬ
кии
-я-
0.0070
| 0,0050
| 1 |
О | |||||||
|
-------- | ----- |
|||||||
| о |
ПО | Вист ость - >5,8 % н - 250 мд | ||||||
| | | ||||||||
/ w I Ау
2,00
см^-сен-спз
Рис. II. 22. Определение проницаемости К и коэффициента турбулентности Р для песчаника Вилкокс [11.22].
URTfL{V,A)-VI*^+M- <1,Л4)
На рис. II. 22 представлены данные по фильтрации газа, обработанные в соответствии с этой формулой. Отрезок, отсекаемый прямой на оси ординат, дает величину IfK, а наклон прямой выражает коэффициент Турбулентности Р- В табл. II. 7 представлены значения коэффициента турбулентности для нескольких керноз, полученные этим способом [II. 21]. На рис. II. 23 нанесены значения коэффициента турбулентности в зависимости от проницаемости [11. 42]. На этом же рисунке нанесены линии постоянных значений пористости, полученные из данных Яничека и Катца (Janicek and Katz) [II. 37], основанных на зависимости коэффициента турбулентности от проницаемости и пористости.
Интегрирование этого выражения между точками 1 и 2 дает
Таблица II. 7
Основные характеристики некоторых сцементированных образцов
9,4Х 1010 32 р'/г
Кг =
К
РО,ф‘/.
| Коэф фициент электро сопротив ления, | Пори стость ф, доли еди |
а, см~~^ | Р. СМ—1 | Проницаемость К, мд | De Кг = 0.5), см | Le/L |
| F | ницы |
Тип образца
| Песчаник Вилкокс |
15,5 | 0,175 |
5,21 X 108 | 2,70 X 10е | 192 |
1.37Х Ю7 | 1,64 |
1,26 |
|
17,4 | 0,158 |
4,00 X 108 | 1,01 X 10е | 250 |
1,65х 107 | 1,66 |
3,48 | |
|
16,6 | 0,160 |
6,76x108 | 3,26 X 10е | 148 |
1.24Х Ю7 | 1,68 |
1,33 | |
| Песчаник Бромайд | 36,2 |
Г,110 | 5,00 XI О10 | 9.19ХЮ7 |
2,0 | 2.16Х108 |
1,99 | 1,05 • |
| 36,2 |
0,110 | 4.17ХЮ10 |
6,53 X Ю7 | 2,4 | 2,34 X Ю8 |
1,99 | 1,38 | |
| 62,5 | 0,030 | 1,08х Ю12 |
2,95x10“ | 0,093 |
6,04 X Ю? | 1,36 |
0,00512 | |
|
86,8 | 0,022 |
2,08х Ю12 | 6,43 X Ю1» | 0,048 |
5.12ХЮ7 | 1,38 |
0,053 | |
|
30,0 | 0,123 |
6,67 X 10° | 1,44х Ю7 | 15,0 | 5,30X10» | 1,92 | 1,95 |
|
| Песчаник Барбанк |
39,1 | 0,150 |
9,09 х Ю9 | 4,30 X Ю7 | 11,0 |
5,18х 10е | 2,41 |
0.901 |
|
34,8 | 0,163 |
2,82 х Ю9 | 1,14 х Ю7 | 35,5 |
8,85 х Ю3 | 2,38 |
1,62 | |
| Песчаник Спраберри | 53,8 |
0,080 | 1,03 XI О12 | 6,56 х 10° | 0,097 | 5,73x107 |
2,07 | 0,119 |
| 60,3 | 0,084 | 9,09 X Ю12 | 5,71 X Ю11 | 0,011 |
2,05 X Ю9 | 2,25 |
0,00441 | |
|
Песчаник Ауткроп |
14,4 | 0,206 |
3,20 х 10» | 2,33 X Ю7 | 31,3 | 5,74 x10е | 1,72 |
0,310 |
| 14,4 | 0,206 | 4,78 X 10» | 2,69 X Ю7 |
20,9 | 4,69 x10е |
1,72 | 0,328 | |
| Песчаник Торпедо |
12,1 | 0,227 |
2,36 х Ю8 | 1,92х Ю5 | 424 |
1,93x10’ | 1,66 |
8,11 |
| 13,4 | 0,228 | 1,97 ХЮ8 | 1,57хЮ5 | 508 | 2,23 X Ю7 | 1,74 |
10,0 | |
| Доломит Браун | 49,8 |
0,143 | 2,13x10° |
2,05x107 | 47,0 |
1,31 ХЮ7 | 2,66 | 1,19 |
|
— | 0,160 | 2,55 X 109 | 5,09 X 10е | 39,2 | ||||
| — | 0,125 | 1.98Х Ю10 |
1,06хЮ8 | 5,4 |
||||
|
64,7 | 0,095 |
9,80 X Ю1» | 2,38х Ю9 | 1,02 |
2,20 х Ю8 | 2,48 |
0,111 | |
|
70,2 | 0,095 |
1.33ХЮ1» | 2,70 X Ю8 | 7,5 |
6,24 X 10е | 2,58 |
0,390 | |
|
68,5 | 0,094 |
4,83X10“ | 8,73 X Ю9 | 0,207 | 1,02 хЮ8 | 2,54 |
0,0714 | |
| Известняк Каньон Риф | 142,5 |
0,051 | 8,20x10“ |
3,39 X Ю10 | 0,122 | 1,03хЮ8 |
2,69 | 0,0677 |
| 123,0 | 0,087 | 9.70Х Ю1» | 2,97 X Ю9 | 1,03 |
3,05 X Ю8 | 3,26 |
0,176 |
Примечание. Данные взяты из [11.21].
Для сравнения данных фильтрации в пористой среде со скоростями в условиях турбулентного режима фильтрации эти данные могут быть представлены о виде зависимости коэффициента трения от числа Рейнольдса подобно тому, как это показано иа рис. II. 24 [II. 21]. При этом коэффициент трения определяется из следующего соотношения:
(II. 16)
Re =
$LW2 ’ ( '
где f — коэффициент трения, безразмерная величина; р — плотность жидкости или газа в г/см3; р — давление в кГ/смг; А—площадь поперечного сечения потока в см2; Р — коэффициент турбулентности в см-1; L — длина в см; W — массовая скорость потока в г/сек.
•вязкость жидкости
Число Рейнольдса определяется из уравнения
где К — проницаемость в мд; или газа в спз.
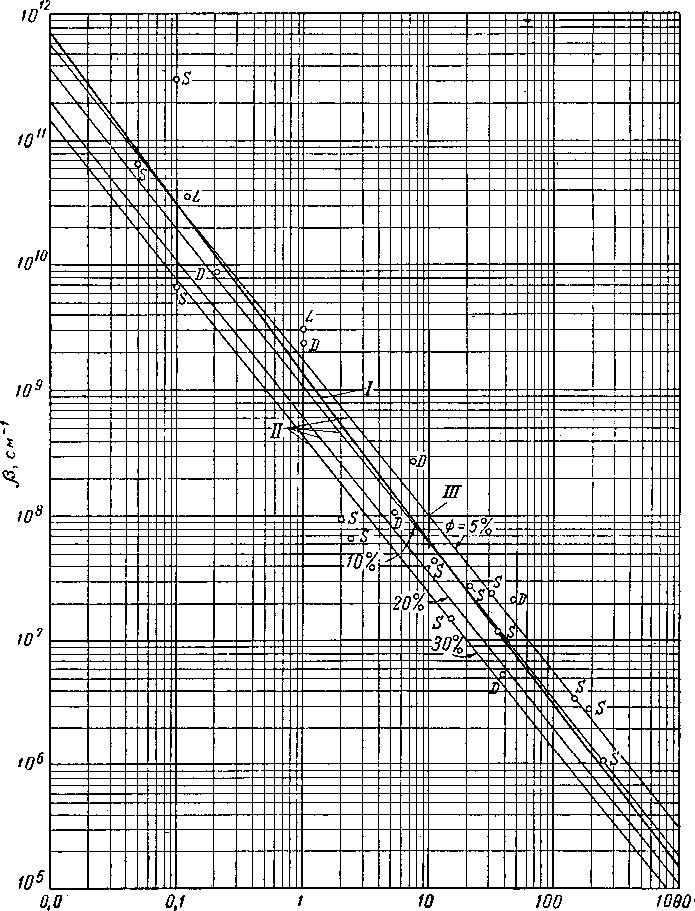
К, мд
Рис. II. 23. Зависимость коэффициента турбулентности от проницаемости
[2; 37, 2; 42].
I — линия, использованная для корреляции данных; II — линии различной пористости [11.37]; III — пористость 5%; D — доломит; L ^ известняк; S —песчаник.
woo
«*>
II
4.
wo
1.0
soo
0,01
0,1
10
|
. —|—Г Т ТТПТ | —1 'Т '1 гпгг | -1-[ 1 '1 1 гтт | Т" г 1 1 1 И L X 1 Z + 2 ; ьЗ Vi ? 5 0 б о 7 |
|
---------- : % “ Чэ | А, о |
09 - | |
| 1 Г » 11111 | \ • 1. » 1-1 J-LL | ¦" 0 о°(Я? 1 III 1.1.11 | оооо®°° ° ° оооооЗ 1 1 1 1 1.1 11 |
fiKW
10
moo
tOjuA
Рис, 11.24. Зависимость коэффициента сопротивления трения от числа Рейнольдса [11.21]
при движении через пористые среды,
/ — песчаник Вилкокс (№ 1-3)- 2 —песчаник Бромайд (№ 4—8); 3 — песчаник Барбанк (№ 9—10)-, 4 — песчаник Спраберрн (J* II— 12) 5 —песчаник Ауткроп (№ 13—14); 6 — песчаник Торпедо (№ 15—16); 7 —доломит Браун (ЛГа 17—22); в—известняк Каньон
(Риф (№ 23—24); 9 — пористые металлы.
1
¦ +
Re =
= 1,0, R = 82,06
8,17
W2
W,
Re =
моль °K On ределить W 8,2 x 10s
1
A =
Пример
Имеется керн диаметром 18,5 мм, длиной 18,5 мм. Его, пористость 15,8%, проницаемость 250 мд. Рассчитать скорость течения воздуха при условии, что давление иа входе в кери составляет 6,8 ата, а абсолютное давление на выходе равно атмосферному (1 ат). Температура воздуха 24° С.
Решение с помощью уравнения (11.14)
Значение коэффициента турбулентности Р из рис. II. 23 равно 8,2Х105 см~К Вязкость воздуха 0,020 спз, а коэффициент сжимаемости может быть взят ¦равным единице.
Таким образом, , данные из расчета следующие: М = 20 г Iмоль, р\ —pf =45,28 ат2, (* =0,020 спз, г = см3 а
Величина 1 • 013 • 420 — переводной коэффициент gc, г • см am • см2 • сек2
Скорость течения W определяем из уравнения (II. 14): 29 X 45,28 X 2,66
2 х 1,0 X 82,06 X 297,2 х 0,020 W X 1,85
T=297,2°K; L=l,85 cm.
= 2,66 cm'3
m
= 0,8096 am ¦сек2/г;
013 • 420 X 1,852
8,2 х Ю5 X 1,85 W2 Решение находим методом подбора величин Предполагая, что W = 0,34 г/сек, будем иметь = 1,29, /=70,6. Значение Re=l,0 является более точным (рис. 11.24). Тогда
Скорость, полученная экспериментально для этого случая, составила 0,23 г/сек, Экспериментальное значение Р равнялось 10,1 Х105, в то время как значение р, полученное из рис. II, 23, составляет 8,2х105 см~‘.
2,66 x 0,020 г0,25’
W2 + 0,2628 W - 0,1272 = 0, W = 0,25 г/сек. Решаем с помощью графика (рис. 11,24) и уравнений (II, 15) и (II. 16):
Р = 8,2 х 105см~х, К = 250 мд, А = 2,66 сма,
[1 = 0,020 спз.
10е X 2,66 X 0,020
P = —(p.8 + 1) 29 00464 г/см3
P 82,055 X 297 X 2 U>UU4D4 г!см >
Pi — Pi = 6,8 — 1 = 5,8 кГ/см2,
64 X 103 X 981 X 0,00464 X 5,8 X 2,662
15,218 W2 + 4W — 1,935 = 0,
8,2 х 10s W х 250
= 3,80 W\
0,8096 W
/ =
Породы, слагающие нефтеносные и газоносные пласты, испытывают давление вышележащих пород, а также давление жидкостей или газа. Эти давления много больше, чем давления, при которых обычно проводятся лабораторные эксперименты. Влияние сжимаемости горных пород на пористость и проницаемость представляет интерес для применения результатов лабораторных экспериментов к вопросам нефтепромысловой практики.
<ь 5
It;
CD Сз
ГО CD =3 <о I
О СЗ
* 5:
> л
>4-0 280 420
Давление, am
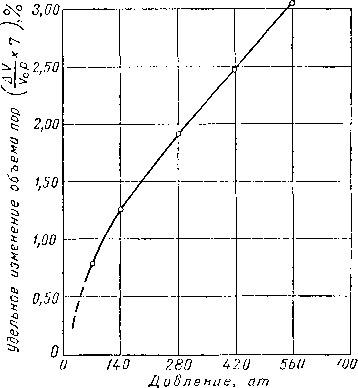
Вопросы сжимаемости горных пород и влияние сжимаемости на пористость и проницаемость были исследованы в работах [II. 19, 11.31, 11.27]. На рис. 25
[II. 31] показана схема прибора для определения сжимаемости горных пород. С помощью этого прибора можно определять сжимаемость породы при увеличении внешнего давления и сохранении внутрипорового объема породы атмосферного давления. Жидкость, выжимаемая при этом из керна, замеряется стеклянной градуированной трубкой. Данные этого типа были получены Карпентером и Спенсером (Carpenter and Spenser) [II. 19] ‘И представлены на рис. II. 26. Иногда наблюдаются гистерезисные явления, иногда песчаннк ведет себя как упругая среда. В пределах 33—63° С никакого влияния температуры на сжимаемость породы не обнаружено. Холл (Hall) [II. 31] также измерял сжимаемость горных пород. Результаты его экспериментов представлены на рис. II. 27 в виде изменения единицы объема пор при изменении давления на I ат.
Кроме того, с помощью прибора, изображенного на рис. II. 25, Холл проводил следующие опыты по определению сжимаемости пористой среды. При поддержании внешнего давления на керн порядка 210 ат определялась разница между количеством жидкости, в действительности полученной из керна, когда давление на жидкость в керне уменьшалось до 105—140 ат, и коли-1,00
0,50
^IQ.
<iL°
| / |
560
700
Рис. II. 26. Сжимаемость песчаника Вудбайн при 63° С [II. 19].
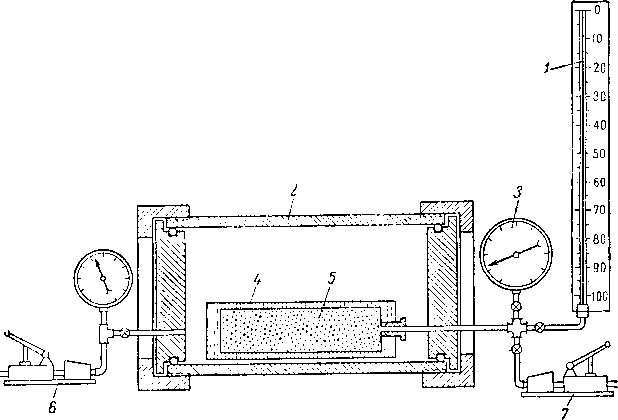
Рис. 11.25. Схема прибора для определения сжимаемости пород [11.31].
WO
с*.
Cj
о
5:
SO
60
<o Ci >*. 4
20
| S, | |||||||||||||||||||||||||||||||
| к |
|||||||||||||||||||||||||||||||
| / | \ |
¦з | |||||||||||||||||||||||||||||
|
s | 3 |
12 | |||||||||||||||||||||||||||||
|
N | ч. | 1 |
9 | 12 | // |
11 | |||||||||||||||||||||||||
| --ч | 10 | ш |
J; | __ | \ | ||||||||||||||||||||||||||
| 2 |
*1 | * | |||||||||||||||||||||||||||||
| Г |
7 | ||||||||||||||||||||||||||||||
| и | |||||||||||||||||||||||||||||||
4 Пористость',%
Рис. 11.27. Уплотнение горных пород в зависимости от давления.
/•—Сан Лндрюс; 2 — Риф; 3 — Тенслип; 4 — Клирфорк; 5 — Каньон риф; 7 — Пело пинто; Н — Бендера; 9 — Бартлесвилл; 10 — Страун; // — Вудбайн; 12 — Торпедо; 13 — Фрио. 1 — известняк; // — песчаник; /// — песчаник (по данным Горного бюро)
§
Рис. 11.28. Эффективная сжимаемость пластовых по-род [П. 31].
L°
/ — пористость в % ; 2 — эффективная сжимаемость поро
ды X 10 (изменение порового объема иа единицу порового объема на атмосферу); / — Сан Аидрюс; 2 ~~ Риф; 3 — Тенслип; 4—Клирфорк; 5 — Каньон Риф; б — Клирфорк (диаметр I"); 7—Клирфорк (диаметр 2"); 8 — Пело пинто; 9 — Бендера; 10 — Торпедо (диаметр 1"); // —Вудбайн; 12 — Торпедо
(диаметр 2"); / — известняк; // — песчаник.
120
100
80
60
U0
20
|
1 | \ | ||||||||||||||||||||||||
| 3 |
|||||||||||||||||||||||||
| X | |||||||||||||||||||||||||
| \ | |||||||||||||||||||||||||
| L | \ | 5 | |||||||||||||||||||||||
| с | |||||||||||||||||||||||||
|
и | о | 9 | |||||||||||||||||||||||
| 5 |
о | ю | 12 |
||||||||||||||||||||||
|
6 | If | ||||||||||||||||||||||||
| о | / | ||||||||||||||||||||||||
| 9 | Л |
||||||||||||||||||||||||
8 Ю 12 /4 16 18 20 22 24 26 Пористость,
Рис. II. 29. Влияние давления обжима иа прониця емость кернов [II. 27].
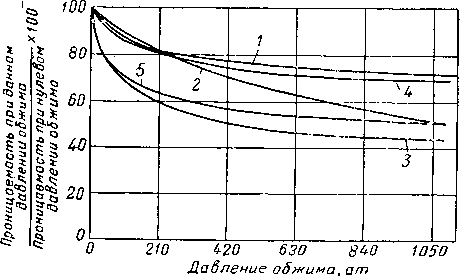
I — К = 3.8С мд; 2 — К — 40.8 мд; 3 — К = 45 мО; 4 - К = = 4,35 мд; 5 — К = G32 мд.
чеством жидкости, которое могло бы быть получено из керна только за счет ее сжимаемости. Это последнее количество жидкости может быть рассчитано по данным ее сжимаемости с учетом поправки на жидкость, нахо>-дящуюся вне керна. На рис. II. 28 приведены результаты исследований Хелла в виде кривой, выражающей зависимость уменьшения единицы порового объема, приходящегося на 1 ат разницы между внешним давлением на керн и давлением на жидкость внутри керна.
Влияние внешнего давления на проницаемость кернов исследовалась Фаттом и Девисом (Fatt and Davis) [II. 27]. В этом случае, пользуясь прибором, аналогичным прибору, изображенному на рис. II. 25, азот при атмосферном давлении пропускали через сухие керны, вставленные в о-правку и обжатые с ботовой поверхности внешним давлением. Данные, приведенные на рис. II. 29, показывают, что при увеличении внешнего давления проницаемость заметно уменьшается.
Метод измерения .коэффициента электрического сопротивления F является одним из методов оценки структуры порового пространства пород-коллекторов. Этот коэффициент был определен Арчи (Archie) [II. 2] как отношение электросопротивления Ro образца пористой среды, насыщенного проводящим раствором, к сопротивлению этого же раствора Rm, имеющего те же размеры и форму, что и образец породы:
/?0
(11.17)
w
Так как течение электричества аналогично потоку жидкости или газа с вязкостью, равной нулю, то в этом случае диаметр пор не является характерной величиной, каковой он является, например, в формуле Пуазейля для случая течения вязкой жидкости. Таким образом, коэффициент электросопротивления зависит только от длины пор и от пористости, а не от проницаемости. Поэтому знание коэффициента электросопротивления позволяет рассчитывать длину пор образцов пористой среды.
г, е е
Ф1.'Т
(II. 18)
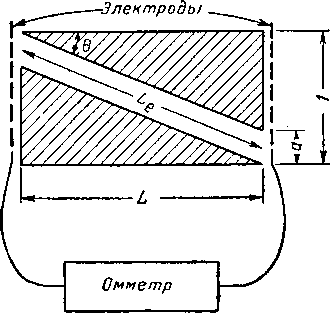
Рис. II. 30. К выводу коэффициента электросопротивления.
[11.20].
/ — люситовая стойка; 2 — фетровая прокладка; 3 — платиновые электроды.
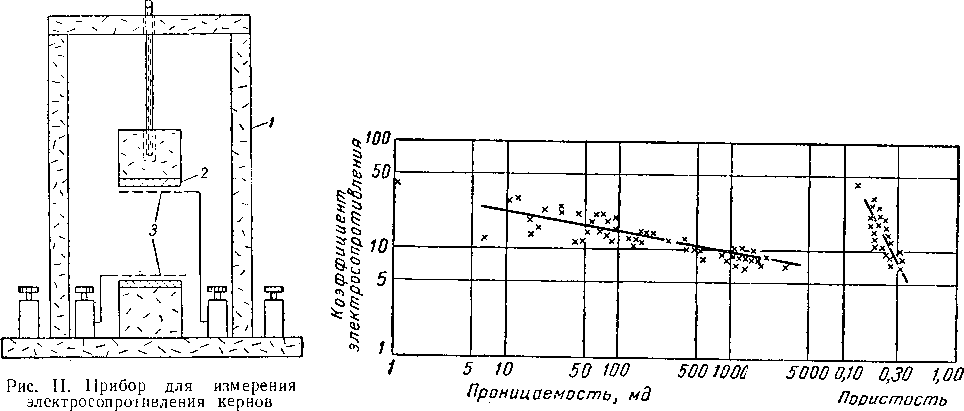
Рис, II. 33. Зависимость коэффициента электросопротивления кернов мексиканского залива от пористости и проницаемости [II. 2].
Величина коэффициента сопротивления F зависит от действительной площади поперечного сечения тгустот образца и от длины пути, отличной от длины образна вследствие непрямолинейности потока. Из рис. II. 30 видно, что сопротивление зависит как от площади сечения пор, отнесенной к общей площади сечения образца, так и от длины пор, отнесенной к длине образца. При этом 1 сопротивление обратно пропорционально площади поперечного сечения пор и прямо пропорционально отношению длины пор к длине керна.
Площадь сечения пор, нормальная к направлению
потока, равна a oos 0 = aj^. Так как пористость равна
Ф=а/1,0, то площадь сечения нормальная к направлению потока, составит ®L/Le. Исходя из этого, сопротивление
' '
' 0L2 ‘
Это уравнение было выведено независимо Уинсау-ером (Winsauer) с соавторами [II. 72] и Корнеллом (Cornell) [II. 20]. Вилли (Wyllie) и Спенглер (Spangler) вывели аналогичное уравнение, основанное на том, что площадь поперечного сечения пропорциональна пористости, а не величине ФЬ/Ье.
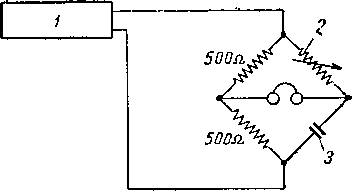
Рис. 11.32. Электрическая схема для измерения электросопротивления [II. 20].
/ — звуковой генератор; 2 — испытуемый керн; 3 — магазин сопротивления.
Значения коэффициентов электросопротивления породы и пористости могут быть использованы для определения коэффициента извилистости Le.'L образцов породы. Типичные данные для сцементированных пористых сред приведены в табл. II. 7. Знание коэффициента извилистости очень важно для понимания движения жидкостей и газов через поровое пространство породы.
Для измерения электросопротивления образца породы этот образец экстрагируется, высушивается и насыщается 0,1 н. раствором КС 1 в дистиллированной воде. Прибор для измерения электросопротивления кернов (рис. II. 31) снабжен платиновыми электродами, кон-тактирующим'и с раствором, насыщающим керн. Электрическая схема для измерения электросопротивления кернов (рис. II. 32) состоит из звукового генератора и мостика Уитстона. Коэффициент электросопротивления вычисляется как отношение сопротивления образца породы к известному сопротивлению такого же объема 0,1 н. раствора КС1.
Пример
Образец породы диаметром 1,84 см и длиной
1,65 см, насыщенный 0,1 н. раствором КС1, имеет при температуре 27,3° С сопротивление 715 ом. Определить коэффициент электросопротивления этого образца.
Решение
0,1 н. раствор КС1 при температуре 27,3° С имеет сопротивление 74,3 ом-м. Поэтому коэффициент электросопротивления •
715 х я X 1,842
F =
15,5.
4 X 1,65 х 74,3
Знание коэффициента электросопротивления пород очень важно при интерпретации данных сопротивления, полученных при электрокаротаже скважин. На рис. II. 33 представлены данные Арчи [II. 2] для песчаников из скважин Мексиканского залива. На рис. II. 34 [I. 14] дано влияние цементации песка и величины пористости на значение коэффициента электросопротивления.
• 1
42
°3
с (о
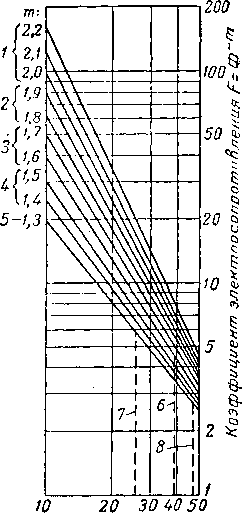
Рис. 11.34. Зависимость коэффициента электросопротивления F от пористости для пород с различной цементацией [I. 14].
/ — высокоцементированые; 2 •-умеренно сцементированные; 3 — слабо сцементированные; 4 — очень слабо сцементированные; 5 — несцементированные; 6 — ромбическая укладка; 7 — гексагональная укладка: 8 — кубическая укладка; 9— коэффи
циент цементации.
Пористость Ф, %
о
*
CJ
у
51
*
О
§
л
Процесс накопления нефти происходит в большинстве случаев в пористых средах, первоначально заполненных водой. В процессе накопления нефти или газа некоторое количество воды будет оставаться в пористой среде. Эта вода называется связанной. Объем пористой среды, занятый связанной водой, нас интересует с точки зрения оценки запасов нефти или газа.
Действительное содержание связанной воды в керне можно узнать, если отбирать керн при бурении с глинистым раствором на нефтяной основе. Из ранних работ, посвященных изучению вопроса о связанной воде, следует отметить работы Пила и Джонеса (Pyle and Jonec) [II. 57] и Шилтхюса (Schilthuis) [II. 63], Результаты их исследований представлены на рис. II. 35 в виде зависимости водонасыщенности кернов от их абсолютной проницаемости.
Количество связанной воды в пористой среде определяется свойствами поверхности твердой фазы и силами, возникающими на границе раздела фаз. Поэтому вопрос о методах определения содержания связанной воды в пористых средах будет рассмотрен после обсуждения вопроса о природе явления омачивания.
/0000
8000
6000
6000.
3000
2000
/ООО
800
600
400
300
200
/00
80
60
40
30
20
/О
8
6
4
3
2
О 10 20 30 40 50 60 70 80 90 /00 Водомасыщенность, % от объег*а пор
Рис. II. 35. Зависимость содержания связанной воды от проницаемости кернов ГП. 63].
I— Анахуак; 2 — Томболл; 3 — Восточный Техас.
§ 9. СМАЧИВАНИЕ ПОВЕРХНОСТИ ТВЕРДЫХ ТЕЛ
(II. 19)
cos 0„
W =
Изоо кто и
I
Изосктон+изонбинолип
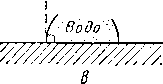
cos 0
= W.
где Sr.T—поверхностное натяжение на границе газ — твердое тело; S,K.T — поверхностное натяжение на границе жидкость — твердое тело; S>K.r—поверхностное натяжение на границе жидкость—газ; 0—угол смачивания.
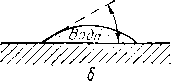
Угол 0 выражает степень смачивания поверхности твердого тела, причем в случае полного смачивания угол, измеряемый в сторону смачивающей фазы, равен 0°, а при полном несмачивании этот угол равен 180°. На рис. 11.37 иллюстрируются результаты
Полное смачивание поверхности или полное его отсутствие можно сравнительно легко представить. Промежуточные значения смачивания требуют уточнения для своей количественной оценки. За меру смачивания поверхности твердого тела жидкостью на границе с газом или другой несмешивающейся жидкостью принимают угол, образованный поверхностью раздела жидкость — газ (жидкость] — жидкостьг) с поверхностью твердого тела [II. 6, II. 29] (рис. II. 36). Поверхностное
Рис. 11.37. Степень смачивания чистого кварца
[п.61.
1 — угол смачивания; 2 ~ воздух; 3 — вода; 4 — изооктан; 5 — изооктан -f- изоквинолин; 6 — изоквннилин. а — полное смачивание (угол смачивания 0°); б — высокая степень смачивания водой (угол смачивания 30°); в — одинаковое смачивание двумя жидкостями (угол смачивания 90°); г ~ низкая стенень смачивания водой и высокая изоквино-лином (угол смэчивания 153°).
натяжение на границах раздела различных фаз находится в равновесии >в соответствии со следующим выражением:
Sr. т = S*. т + S*. г cos
Воздух
^В од о
штшт.

Рис. 11.36. Угол между двумя фазами на твердой поверхности как мера смачивания.
Мзоквинолин
Беннера и Бартелла (Benner and В artel 1) [II. 6, II. 7], показывающие, что действительно можно наблюдать различные значения угла смачивания, находящиеся в пределах 0—180°. Поверхности, смачиваемые водой, называются гидрофильными, а несмачиваемые—гидрофобными.
Тот факт, что вода хорошо смачивает кварц и кальцит, является причиной наличия в большинстве нефтяных 'пластов связанной воды. Адсорбция на поверхности твердой фазы сложных органических веществ, таких, как асфальты, изменяет смачиваемость [11.40]. Поэтому некоторые нефтяные пласты могут содержать малое количество связанной воды или вовсе не содержать ее, когда характеристика смачивания поверхности породы изменена вследствие отложения на ней таких веществ из нефти. Необходимо отметить, что в некоторых случаях вода может остаться в пористой среде в процессе аккумуляции нефти вследствие конфигурации перового пространства породы независимо от характеристики смачивания твердой поверхности. Полагают, что в газоносных пластах порода смочена водой и содержит связанную воду. Хок, Рзаса и Вуд (Hough, Rzasa and Wood) [II. 36] установили, что при некоторых условиях вода не смачивает кончик из нержавеющей стали, который они использовали для измерения поверхностного натяжения воды на границе с метаном при пластовых температурах и давлениях. Вполне возможно, что при определенных условиях вода не будет полностью смачивать на границе с газами и песчаник.
Слобэд и Блюм (Slobad and Blum) [II. 64] предложили метод определения смачиваемости пористых сред, сущность которого заключается в следующем: вода 'вытесняется нефтью и нефть вытесняется воздухом. Зная давления вытеснения 1 в этих двух опытах, а также значения поверхностного натяжения на границах раздела нефть — вода и нефть — воздух, можно определить число смачивания W из соотношения
где 0Н„ — кажущийся угол смачивания на границе нефть—вода; 0Г н —кажущийся угол смачивания на границе газ—нефть; рИ.в, рг-н — давление вытеснения соответственно для случаев вытеснения воды нефтью и нефти воздухом; ог н —поверхностное натяжение на границе газ—нефть; он в — поверхностное натяжение на границе нефть—'вода.
Кажущийся угол смачивания твердой поверхности водой на границе с нефтью 0„ в может быть подсчитан из выражения [II. 21] в предположении, что cos 0r-H.= 1, т. е. нефть полностью смачивает поверхность твердой фазы на границе с воздухом:
При полном смачнвании водой 0 = 0°, а число смачивания W — 1,0. При промежуточном смачивании, когда 0 =90°, W = 0. В табл. II. 8 приведены значения углов смачивания, полученные при помощи данного метода. Слобэд и Блюм (Slobad and Blum) определили также, что обработка кернов в лаборатории может привести к значительному изменению их смачиваемости.
I Давление вытеснения — это минимальное давление, необходимое для вытеснения из пористой среды несмачивающей жидкостью жидкости, смачивающей поверхность этой среды.
¦V. н Pr. н°н. 1
Рн. п°г. н
(II. 21)
(II. 20)
| № керна |
Тип породы | Давление вытеснения, кГУсм2 |
Число смачи ва ния** |
Кажущийся угол смачи* ван и я | № керна | Тип породы |
Давление вытеснения, кГ/см2 | Число смачи ва ния** | Кажу щийся угол смачи вания | ||
| воздух— нефть | нефть— вода | воздух- нефть |
нефть— вода | ||||||||
|
BTL | Девонский известняк | 0,455 |
0,427 | 0,84 |
33° | 1545 |
Искусственный | 0,047 | 0,020 | 0,37 |
68 |
| BTN |
0,476 | 0,434 | 0,81 | 36 |
|||||||
| ВТО |
0,437 | 0,420 |
0,85 | 31 |
1592 | Клирфорк |
0,050 | 0,017 |
0,30 | 73 | |
|
ВТР | 0,448 |
0,273 | 0,54 |
57 | 1593 |
0,038 | 0,022 |
0,53 | 58 | ||
|
1588 | Песчаник Яте | 0,060 | 0,022 |
0,33 | 71 |
1594 | Известняк |
0,111 | 0,022 |
0,18 | 80 |
|
1589 | 0,060 |
0,021 | 0,31 |
71 | 1595 |
0,203 | 0,032 |
0,14 | 82 | ||
|
1590 | 0,060 |
0,022 | 0,32 |
71 | |||||||
| 1591 |
0,070 | 0,028 | 0,36 | 69 |
1620 | Песчаник Тенслип | 0,060 |
0,015 | 0,22 |
78 | |
| 1621 |
0,060 | 0,015 | 0,22 | 78 |
|||||||
| 1542 | Алунд (R А-1139) | 0,049 |
0,017 | 0,32 |
72 | 1622 |
0,048 | 0,008 |
0,16 | 81 | |
|
1543 | 0,049 |
0,020 | 0,36 |
69 | 1623 |
0,060 | 0,019 |
0,28 | 74 | ||
|
1544 | 0,048 |
0,028 | 0,52 |
59 | |||||||
* Испытаниям кернов на смачиваемость предшествовала обычная их экстракция хлороформом, эа исключением кернов из алунда, которые регенерировались нагреванием их до 760° С в течение 3 ч.
** Поверхностное натяжение на границе раздела воздух — нефть равно 24,9 дин/см, нефть — вода—28,0 дик/см. Данные взяты из [II.64.J
Для выяснения неполного вытеснения жидкости из пористой среды необходимо рассмотреть вопрос о поверхностном натяжении на границе раздела жидкость— жидкость или жидкость — газ. Поверхностное натяжение жидкости на границе с газовой фазой измеряется методом капиллярного подъема жидкости в стеклянной трубке малого диаметра (рис. 11.38). Если жидкость омачи-
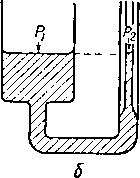
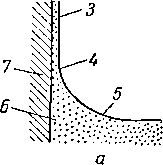
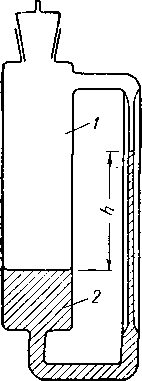
Рис. II. 38. Определение поверхностного напряжения методом капиллярного подъема.
/ — пар; 2 —жидкость: 3 — пленка жидкости, смачивающая стенки капилляра» 4—натяжение в этой точке; 5 — мениск: 6 — жидкость; 7 —стенка капилляра.
вает поверхность стеклянного капилляра, то она подни-мается :в трубке. Вес столба жидкости, превышающего уровень свободной поверхности, уравновешивается силами 'Поверхностного натяжения, приложенными к периметру смачивания поверхности капилляра.
Уравнение равновесия записывается в виде
cos 0а (2кг) = itr2h (рж — рИ) g, (II. 22)
где а—поверхностное натяжение в дин/см; г — радиус трубки в см; h — высота капиллярного подъема в см; Рж и Рп—плотность жидкости и пара соответственно в г/см3; g — ускорение силы тяжести 980,6 см/сек2;
0 — угол смачивания поверхности капилляра жидкостью на границе с собственным паром. В случае полного смачивания 0=0.
Чтобы привести уровень жидкости в кашилляре до уровня свободной поверхности жидкости над уровнем жидкости в 'капилляре, необходимо создать некоторое давление. Величина этого давления определяется из соотношения
2г.Г а = nr*hg (рж — ри) = тт2 (р2 — Pl) gc< (II. 23)
где р — давление в Г/см2; gc — переводной коэффициент, равный 980,6 г • секР/г ¦ см.
Из этого уравнения получим
бс
Разность давления рг — Pi называется капиллярным давлением р0. Если угол смачивания капилляра жидкостью не равен 0°, то
2а cos 6
Рс=—--• (П.25)
Когда на жидкость в капилляре действует некоторое давление, понижающее ее уровень до уровня свободной поверхности, то в этом случае па o6g стороны мениска имеется разность давлений рс.
Для капилляров нецилиндрической формы капиллярное давление может быть выражено через кривизну
мениска:
где RI и R2 — главные радиусы кривизны мениска, показанные на рис. II. 39 [II. 471.
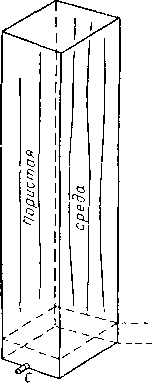
Рассмотрим случай, когда пористая среда насыщена
. / жидкостью (рис. 11.40).
/ / При этом начальная насы-
\ ______/ щенность жидкостью соот-
Д т_ *А ветствует линии А. Позво-
лим жидкости вытекать че-/ ^2 рез отверстие С. При уста-
' ' новлении равновесия насы-
щенность пористой среды
--жидкостью будет соответ-
¦1 ствэвать кривой В. В точке
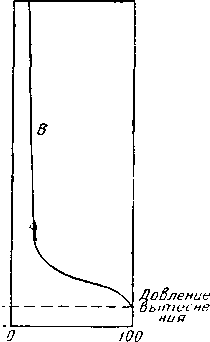
С и ниже насыщенность жидкости будет равна 100%. Только некоторые крупиые поры, расположенные выше \ точки С, будут содержать R' 1 жидкость. Для данного рас-
1 ' цределения пор по разме
рам кривая изменения насыщенности имеет форму, указанную на рисунке. Bepj тикальная часть кривой представляет собой насы-Рис. 11.39. Радиусы кри- Щенность, обусловленную
визны мениска между наличием непрерывных пор
двумя частицами [II- 47]. малого диаметра. Кроме то-
У-твердое тело; 5-жидкось г°- жидкость может удер
живаться в крупных порах, сообщающихся с каналами, радиусы кривизны менисков в которых малы.
К настоящему времени проведено большое количество исследований с целью определения содержания в кернах связанной воды методам капиллярного давления [11.47, 11.68, 11.33, II. 9, 11.70, 11.51, 11.34, 11.62, 11.16]
Насыщенность а
Насыщенность wudxocmu, °/о
Рис. 11.40. Распределение жидкости в пористой среде после ее дренирования.
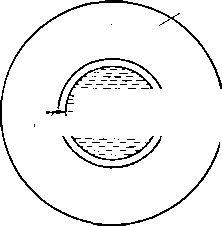
Так как процесс вытеснения воды сходен с процессом, который происходит в пласте во время аккумуляции газа, то иногда он упоминается как метод воспроизведения условий. Типичный прибор для определения содержания связанной воды методом капиллярного давления показан на рис. II. 41. Образец породы, насыщенный водой, приводится в контакт с тонкой пористой пластинкой, предварительно насыщенной водой. В камеру подается давление воздуха или какого-либо газа, и вода начинает вытесняться из керна. При данном давлении
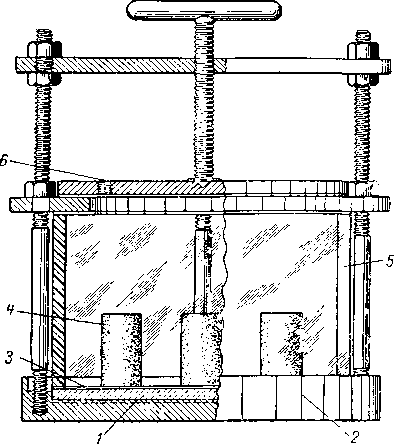
Рис. 11.41. Прибор для определения связанной воды методом капиллярного давления [11.41].
1 — керамическая пластинка; 2 — сосуд для воды; 3 — слой Клииекса; 4 — ксрп; 5 — люснтовап трубка; 6 — отверстие для входа воды, насыщенной воздухом под давлением-
газа образец выдерживается до достижения равновесных условий, после чего взвешиванием определяется содержание в нем воды. Далее образец снова помещается в камеру и давление газа устанавливается на более высоком уровне, чем прежде. Вода вытесняется из керна газом вниз до уровня пористой пластинки подобно тому, как на рис. II. 38, б давление газа приводит к уменьшению высоты капиллярного подъема. Размеры пор пористой пластинки должны быть очень малыми, чтобы уменьшить возможность вытеснения из них жидкости газом даже при сравнительно высоком давлении. На рис. II. 42 приведены типичные кривые капиллярного давления, а на рис. 11.43 и в табл. II. 9 представлены подобные же данные для кернов из скв. А [11.68], вскрывшей миоцен в Луизиане.
Как правило, керны с более высокой проницаемостью имеют более низкие значения ъодонасыщенности.
При увеличении давления воздуха или увеличении капиллярного давления в керне его водонасыщенность уменьшается точно так же, как это наблюдается в пласте по мере удаления от уровня свободной поверхности воды. Обычно в лабораторной практике для определения капиллярного давления используются вода и воздух. В пластовых же условиях капиллярное давление возникает на границе раздела пластовой воды с природным газом высокого давления. Соотношение капиллярных давлений И поверхностных натяжений на этих границах
| Кри- вые |
Пори стость, % |
Прони цае мость, мд | Порода |
| 1 | 22,8 | 175,0 |
Песчаник |
| 2 |
12,8 | 35,0 | » |
| 3 | 16,4 |
21,0 | » |
|
4 | 5,3 | 0,1 |
|
| 5 | 18,8 | 860,0 | Доломит |
| в | 14,7 |
3,8 | » |
Таблица П. 9 Значения водонасыщенности кернов из скв. А
| А |
Высота керна над | Водонасыщенность, % от объема пор | ||||||
| m X о. 01 * |
а О 2 <и го Я X X о 0.0$ С « | А Н О ь CJ X а Is | уровнем свободной поверхности воды, м | Давление, кГ/см2 | по методу перегонки (1) | по соле ности воды (2) |
капил ляр ным мето дом (3) | разность между (3) и (2) |
| 1 |
29 | 17,6 |
23,8 | 4,13 |
89 | 71 |
74 | +3 |
|
2 | 312 |
29,3 | 22,6 |
3,92 | 28 |
23 | 23 |
0 |
| 3 |
382 | 22,3 |
21,3 | 3,71 |
52 | 37 |
37 | 0 |
|
4 | 518 |
28,1 | 20,1 |
3,50 | 29 |
34 | 33 | — 1 |
| 5 |
250 | 23,0 |
18,6 | 3,29 |
53 | 36 |
38 | + 2 |
|
6 | 63 |
16,0 | 16,5 |
2,87 | 73 |
61 | 61 |
0 |
| 7 |
2556 | 27,2 |
15,5 | 2,73 |
36 | 28 |
28 | 0 |
|
8 | 23 |
20,0 | 14,6 |
2,59 | 82 |
59 | 59 |
0 |
| 9 |
319 | 25,7 |
13,1 | 2,31 |
44 | 32 |
27 | —5 |
|
10 | 1830 |
31,1 | 12,2 |
2,17 | 19 |
20 | 19 | — 1 |
| 11 |
550 | 27,1 |
11,3 | 2,03 |
47 | 44 |
40 | —4 |
|
12 | 1490 |
27,2 | 10,7 |
1,82 | 44 |
38 | 38 |
0 |
| 13 |
1118 | 31,0 |
10,1 | 1,89 |
30 | 25 |
24 | — 1 |
| 14 | 1730 |
32,6 | 9,8 |
1,75 | 27 |
23 | 24 | + 1 |
| 15 |
540 | 27,9 |
9,5 | 1,68 |
35 | 29 |
27 | —2 |
|
16 | 1048 |
28,6 | 9,1 |
1,68 | 36 |
34 | 25 |
—9 |
| 17 |
410 | 27,5 |
8,8 | 1,61 |
38 | 37 |
35 | —2 |
|
18 | 1960 |
27,4 | 8,5 |
1,61 | 33 |
34 | 34 |
0 |
| 19 |
2238 | 29,8 |
7,3 | 1,40 |
36 | 34 |
26 | —8 |
|
20 | 1120 |
30,9 | 6,7 |
1,33 | 32 |
28 | 30 | 1 +2 |
| Сред нее | — |
— | — |
— | 43 |
36 | 35 | — 1,3 |
Примечание- Данные взяты из [11. 68].
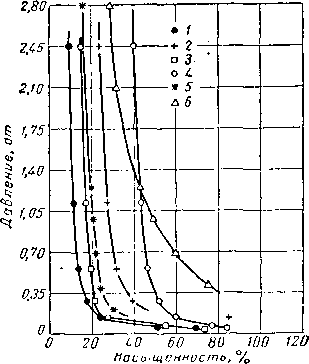
Рис. 11.42. Кривые капиллярного давления.
раздела для условий пласта и лаборатории для одного и того же керна равно
Рс„п C<Jm,cos0™i
где Рс — капиллярное давление; h — высота расположения керна над уровнем свободной поверхности воды в м; рш, рг —плотность жидкости и газа ,в г/см3; g/gc— 1,0 г/г (индексы «пл» и «лаб» относятся соответственно к пластовым и лабораторным условиям).
Например, для керна, отобранного из газового пласта, расположенного в 10 м над свободным уровнем контакта газ—«ода в пористой среде, потребовалось бы в лаборатории для воспроизведения насыщенности капиллярного давления, равного 1 ат,
Торнтон и Маршалл (Thornton and Marschall) [11.68] вычислили лабораторные значения капиллярных давлений для соответствующего положения кернов над свободным уровнем воды (см. табл. II. 9), предположив, что плотности воды и нефти равны 1,076 и 0,508 г/см3 и что давление на уровне свободной поверхности воды равно 0,1 ат.
Содержание связанной воды в кернах зависит главным образом от их проницаемости, Важным фактором
^ (Рж Рг)пл^
Го 7, ’
Салабсо:50лаб
10 X 1 10
лаб
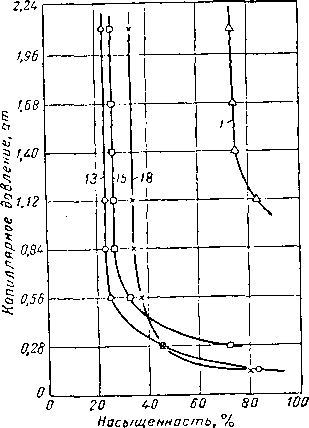
Рис. 11.43. Кривые капиллярного давления для кернов скв. А [II. 68].
Зпл “S 0Пл
(11.27)
слаб алаб COS 0лаб
Др =
1 am.
90

Рис. 11.44. Зависимость содержания связанной воды, определенной методом капиллярного давления, от проницав'
мости сухого керна [1.36].
Значения водонасыщенности взяты при давлении воздуха 2,8 ат.
80
70
I 60
Сэ
§ 50 %
0
1 40
о
л
03 30
20
10
О
0,00! 0,0/ 0,/ 1,0 Ю ЮО W00
Проницаемость сухого керна, мд
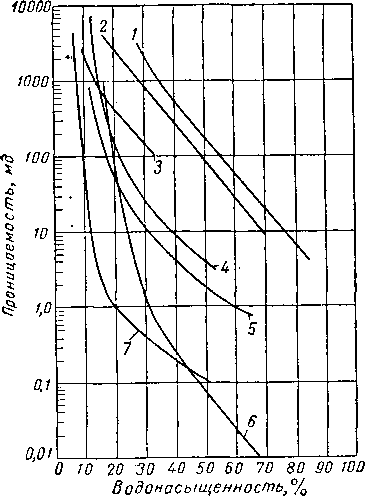
Рис. 11.45. Типичные кривые содержания связанной воды в зависимости от проницаемости.
/ — Анахуак [II. 631; 2 и 3 — миоцен Луизианы [11.68 1: 4 — Восточный Техас [11.63];
5 — песчаник Тенслип II. 70; 6 — доломит
Хьюготон [I.36J; 7 — доломитизированный известняк Ледук [II. 62].
также является структура внутреннего пространства пористой среды.
На рис. 11.44 приведены результаты опытов по определению содержания связанной воды в образцах доломита методом капиллярного давления. Пористость этих кернов представляет собой комбинацию первичной пористости и пористости растворения. В песчаниках содержание связанной воды существенно зависит от количества глинистого материала.
На рис. 11.45 даны типичные кривые зависимости содержания связанной воды от проницаемости по;ристых сред для различных месторождений. Следует помнить, что кривые, приведенные на этом рисунке, дают усредненные значения связанной воды. Несмотря на то, что разброс точек на этих кривых несколько меньше, чем на графике .рис. 11.44, для всех естественных пород этот разброс имеет место. Ричардсон, Перкинс и Особа (Richardson, Perkins and Osoba) [II59] показали влияние геологического возраста пород на характеристики кернов.
Для определения зависимости капиллярного давления от насыщенности часто применяют центрифугу [II. 34, II. 65, II. 50]. В этом случае центробежные силы, приложенные к жидкости, являются аналогом давления, создаваемого газом. На рис. 11.46 [11.65] изображен кер-нодержатель, применяемый в этих экспериментах, а на рис. 11.47 дана зависимость количества воды, вышедшей из керна, от времени для скорости вращения центрифуги, соответствующей давлению воздуха 2,5 ат. Обычно опыты проводятся при нескольких выбранных скоростях вращения центрифуги в течение времени, достаточного для получения равновесия, характеризующегося постоянством количества вытесненной из керна жидкости.
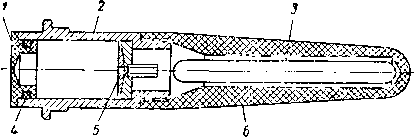
Рис. 11.46. Кернодержатель для определения капиллярного давления с помощью центрифуги [II. 65].
I — изолирующая крышка; 2 — корпус кернодержате-ля; 3 — смотровое окно; 4 — уплотнительное кольцо; 5 —¦ опорный диск; 6 — корпус трубки.
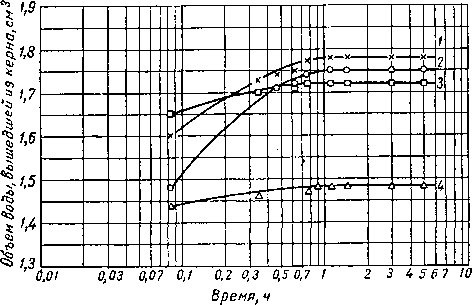
Рис. 11.47. Изменение объема воды, вышедшей из керна, во времени при центрифугировании со скоростью 2300 об/мин в системе вода — воздух [II. 65].
/ — К = \т мд\ 2 — К = 1140 мд\ 5 — А = 2710 мд; 4 — К =
- 2210 мд.
На рис. II. 48, взятом из работы Слобэда, Чамберса и Прина (Slobad, Chambers and Prehn) [11.65], сравниваются результаты, полученные с помощью центрифуги, с результатами, полученными методом капиллярного давления. В некоторых случаях в качестве вытесняющей фазы используются нефть или другие углеводородные жидкости.
Маркс (Marx) [II. 50] предложил метод определения скорости вращения центрифуги, обеспечивающей вытеснение жидкости из керна в условиях лаборатории, эквивалентное вытеснению в пласте. Капиллярные концевые эффекты для модели и пласта будут одинаковыми, если имеет место соотношение
h = ~hm, (11.28)
где /гт — высота образца, помещенного в центрифугу; h — высота модели или пласта; а — ускорение на центрифуге; g — ускорение силы тяжести.
Когда концевые эффекты значительны, соотношение между временем t для пласта или физической модели
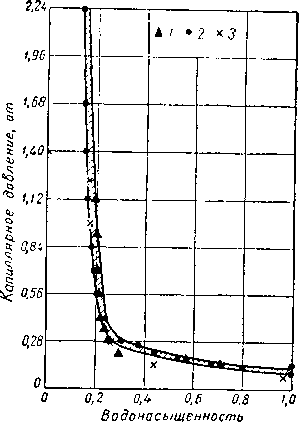
Рис. 11.48. Сравнение кривых капиллярного давления, полученных с помощью центрифуги и обычным капиллярным методом [11.65]. Образец К'иозд=494 мд; Ф=22,5%. Ф = 22,5 % ¦
/ — на центрифуге (1-й опыт); 2 — на центрифуге (2-Й опыт): 3 — капиллярным методом.
и временем tm для центрифугируемого образца может быть получено из выражения
< = (-§-)* - <”-29> Маркс показал, что при центрифугировании образца длиной 2,92 см со скоростью 525 об/мин (расстояние от оси вращения центрифуги до образца равно 16,8 см) в моменты времени, связанные соотношением (11.29), получается та же текущая .насыщенность, что и для модели длиной 154 см. Отношение времен определяется с помощью формул (11.28) и (11.29):
Время, затрачиваемое па центрифугирование, в 2790 раз меньше времени, необходимого для проведения опыта на образце длиной 154 см. Скорость вращения центрифуги вычисляется по формуле
— = I.I18 X Ю-5^2/-, (11.30)
g
где N — скорость вращения центрифуги в об/мич; г—средний радиус центрифуги в см;
/V = 1 / — ---г = 525 об/мин.
У 2,92 16,8 X 1,118 X 1(Г5
10 5 ч
« 5s R * ^ ч* ^ S,
6 jj n,
5е?
sl
2 I-
5s
§
0 §
0)
5
1.6
1,2
0,8
ол
- = 5.
§ 5
ПЭ Сз
0) ч'
5: ^ 0)
I
гь Сз
^ а * ^ I
=3
С
?
0
W0
Таким образом, если давление ртути при вытеснении воздуха ртутью в 5 раз больше давления воздуха при вытеснении воды воздухом, то насыщенность кернов соответствующими фазами (воздухом в первом случае и водой во втором случае) может быть одинаковой, как это видно из рис. 11.49 [11.56]. Преимуществами этого метода являются быстрота проведения эксперимента и возможность создания высоких давлений. Кроме того, он может быть применен для определения капиллярного давления по обломкам и небольшим кусочкам керна. По кривой, соответствующей нагнетанию ртути, может быть рассчитана проницаемость керна по следующей формуле:
Парселл (Purcell) [II. 56] предложил метод измерения капиллярного давления путем нагнетания в керн ртути. При этом используется аппаратура, подобная изображенной на рис. II. 7. Соотношение между капиллярными давлениями на границах раздела ртуть—воздух и вода—воздух равно
капиллярное давление ртуть — воздух капиллярное давление вода — воздух — 480 cos 140°
70 cos 0°
(11.31)
S=100
| О | |||||||||
|
\ | |||||||||
|
\ | |||||||||
| к | |||||||||
| / | |||||||||
| :Х*о-< | |||||||||
| —о- |
20
80
АО*Н2О^60
БО'-Нд-'-ЬО
80
20
100
О
S — насыщенность в %; рс — капиллярное давление, измеряемое по давлению нагнетаемой ртути, в ат.
Коэффициент С может быть определен по стандартному образцу породы и затем использован для работы на небольших кусочках той же породы.
К = 0,66 СФ
(II. 32)
О Р с
где К—проницаемость в мд\ С — коэффициент, зависящий от характера породы (для пласта Полакси равен 0,216, для верхнего песчаника); Ф—пористость в %;
Насыщенность жидкостью
Г ‘Ё
I „2 '
Рис. 11.49. Сравнение кривых капиллярного давления для систем ртуть “ воздух и вода — воздух [11.56].
Песчаник Фрио; К — 170 мд, Ф = 26 % •
§ 12. СООТНОШЕНИЕ МЕЖДУ КОЭФФИЦИЕНТОМ ЭЛЕКТРОСОПРОТИВЛЕНИЯ ПОРОДЫ, КАПИЛЛЯРНЫМ ДАВЛЕНИЕМ И ПРОНИЦАЕМОСТЬЮ
(II. 34)
Ф
A Pf)
32 ?.ц
Возможность существования функциональной связи между коэффициентом электросопротивления, капиллярным давлением и проницаемостью обусловлена тем, что все эти величины определяются размерами пор и структурой порового пространства. Коэффициент электросопротивления породы связан с эффективной длиной пор, а капиллярное давление является функцией распределения пор по размерам. Поэтому эти величины могут быть использованы для определения проницаемости, которая в свою очередь зависит как от длины, так и от диаметра пор. Подобное соотношение особенно необходимо в случае, когда испытывается недостаток в данных по проницаемости и когда имеются небольшие обломки интересующей нас породы.
Закон Пуазейля для течения вязкой жидкости по капиллярам дается в виде
8с*>2, (-
(II. 33)
где v — скорость, измеренная на основании общих размеров образца породы.
Необходимо отметить, что существует менее точная формула для определения эффективной скорости, которая широко применялась как до, так и после появления
v
[П. 18].
Неизвестные величины De, ve и Le могут быть исключены из закона Пуазейля, если вместо них подставить их значения из формул (11.18), (11.34), (11.25), тогда
Эффективная площадь потока при течении жидкости будет той же, что и эффективная площадь при течении через образен электрического тока. Карман (Сагшап) [II. 18] выражает эффективную скорость в виде
работы Кармана. Дюпюи предположил, что
v-b Ф? ’
где ve—эффективная скорость в поровом канале; De — эффективный диаметр порового канала; Д pt — перепад давления; Le — эффективная длина порового канала; —вязкость жидкости.
(a cos 0)2 (— Д pf)
^ flscpI
(II, 35)
Таким образом, скорость течения через поровые каналы, в которых капиллярное давление равно Рс, дается уравнением (11.35), Доля пор такого размера от всего количества пор составляет (1Ф, Объемная скорость течения жидкости или газа через эти поры
Обычно для определения численного значения интеграла требуется графическое интегрирование.
Сопоставляя выражение (11.37) с законом Дарси, представленным уравнением (11,2), можно определить проницаемость:
(a cos О)2 (— Дpj) А 2ц FLp]gc
d<S, (II. 36)
dQ — vAdQ =
(a cos О)2 2 Fgc .
dФ
К-
(II. 38)
где А — площадь поперечного сечения образца.
При интегрировании уравнения (II. 36) получим общую скорость движения по пора.м всех размеров. При этом следует помнить, что рс зависит от насыщенности или от Ф в соответствии с кривой капиллярного давления:
Если К выражено в миллидарси, а в дин/см, пористость в долях единицы и давление в атмосферах, то уравнение (11.38) примет вид:
(а cos 0)2 (— Др^ А d0
0,0494 (a cos О)3F
№
(II. 37)
Q =
(II. 39)
К =
Р2с
2ц FLg(
S 13. ДВУХФАЗНОЕ ТЕЧЕНИЕ. ОТНОСИТЕЛЬНАЯ ПРОНИЦАЕМОСТЬ
При добыче нефти из пласта в пористой среде происходит одновременное течение нефти и газа. При разработке газовых пластов вместе с газом движутся конденсат и вода. Простейший способ изучения двухфазного течения состоит в рассмотрении движения данной фазы в условиях двухфазного потока по сравнению с движением в случае, если эта фаза полностью насыщает поровое пространство. Отношение проницаемости породы для одной из фаз при двухфазном течении к проницаемости породы для этой же фазы при однофазном потоке называется относительной проницаемостью.
Изучению совместного течения в пористой среде двух и более фаз посвящено большое количество исследований [II. 8, II. II, II. 12, II. 32, II. 45, II. 46, II. 48, II. 52,
11.53, 11.54, 11.58, II. 61, II. 74]. В данном разделе лишь кратко рассматривается этот вопрос.
Рассмотрим одновременное течение двух фаз в образце пористой среды (рис. 11.50). При фильтрации жидкости в пористой среде, полностью насыщенной этой жидкостью, определяется проницаемость Кж этой среды для данной жидкости. При совместном течении в пористой среде газа и жидкости (воды или нефти) для вычисления проницаемости среды для каждой из фаз используются соответственно и фазовые скорости. Деление этих фазовых проницаемостей на Кж дает значение относительных л рон иц а ем о сте й.
Основным фактором, от которого зависят относительные проницаемости, является насыщенность порово-го пространства фильтрующимися фазами. На рис. II. 51 представлены типичные кривые относительных проницаемостей для газа и жидкости, одновременно фильтрующихся через сцементированные и 'несцементированные
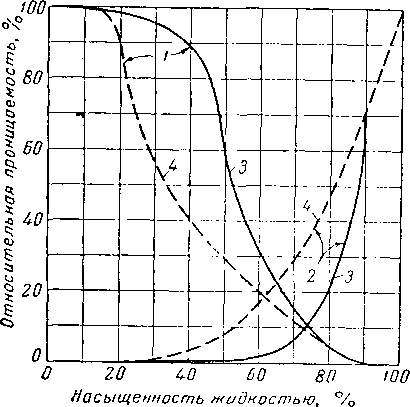
Рис. II. 51. Кривые относительных проницаемостей для сцементированных и несцементированных песков [II. 8].
/ — газ; 2— жидкость; 3 — сцементированный; 4 несцементированный песок-
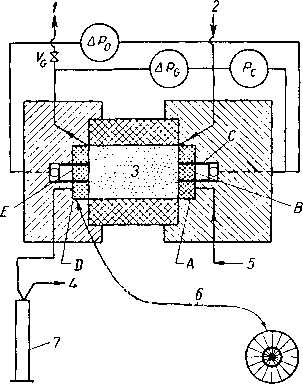
Рис. 11.50. Схема прибора для изучения двухфазного течения [11.54]. I —- выход газа; 2 — вход газа; 3 — керч; 4— в атмосферу; 5 — вход нефти; 6 — фарфоровая пластинка; 7 — мерный цилиндр,
а?
*сГ
Cj
*
<ь
Cl
5з
5:
с*
?
§
5:
¦о
с;
¦ <ъ
80
-о
и
сэ
S:
и
сэ
ST
5:
сэ
?
о;
сэ
5:
¦о
е
и
Cl
5:
е
80
60
60
40
5 20 I
О
о
О 20 40 60 80 100
Нефтенась1щенность,°/Оо5. пор
Рис. II. 52. Кривые относительной проницаемости при вытеснении нефти газом при разных перепадах давления [II. 54].
песчаники. Из этих кривых видно, что газ не будет двигаться до тех пор, пока газонасыщенность не достигнет величины порядка 10—15%. Насыщенность жидкостью порового пространства, при которой жидкость остается еще неподвижной, составляет 30—45%. Обычно сумма относительных проницаемостей, соответствующих определенному значению насыщенности, значительно меньше 100%.
Из других важных факторов, влияющих на величины относительных проницаемостей, следует указать на характер пористой среды, свойства самих фаз и градиент давления. Из рис. II. 52 можно заметить, что увеличение перепада давления приводит к уменьшению насыщенности керна вытесняемой жидкостью ¦. Браувеллом
| Г.............А йР ~ В мм бод.cm п ^i375Л | ||||
| Г» |
a Kg •Х0) |
6750ji /4 | ||
|
а | ||||
| \ | у / | 'п / • / | ||
|
Образец П К~4,18д .....1...... | W*' |
t | ||
Рис. II. 53. Кривые относительной проницаемости при наличии и при отсутствии связанной воды [11.48].
I— газ: 2— нефть; 3 — 15—25 % связанной воды; 4 — без связанной воды.
(Browell) и Катцем (Katz) был предложен независимый метод трактовки двухфазного течения, вносящий ясность в вопрос о влиянии перепада давления на остаточную насыщенность пористой среды жидкостью [II. 10]. Влияние третьей фазы показано на рис. 11.53 [11.48].
Фатт (Fatt) [II. 28] предложил сетчатую модель связанных между собой трубок разных радиусов. Эту модель он использовал для исследования кривых капиллярного давления и для объяснения явления относительной проницаемости.
tазонасыщенность, % оЬ. пор 100 80 ВО 40 20 О
J00
40
20
| ......— Ч > | \ | / / | ||
| V \ |
2i | ' / ~7 | ||
|
- | °/ у |
/ / | ||
|
А 3 'ч | -До/ ч - | / V | ||
| о |
ч* д - | wSJ5-- |
0 20 40 60 80 100
Не ср те насыщенность, % об. пор
§ 14. РАСПРЕДЕЛЕНИЕ ПОРИСТОСТИ И ПРОНИЦАЕМОСТИ
Балнес (Bulnes) [II. 13] использовал статистические методы обработки данных анализа кернов доломитизи-рованного известняка Фуллертон. Для любого интервала значений пористости имеется определенное возможное распределение проницаемости, как это показано на рис. II. 54. На рис. II. 55 представлена кривая, выражающая зависимость вероятной проницаемости, превышающей I мд, от пористости доломитизированного известняка Фуллертон. Подобные методы анализа жернового материала дают более полную оценку продуктивного порового пространства пласта.
Проницаемость, мд
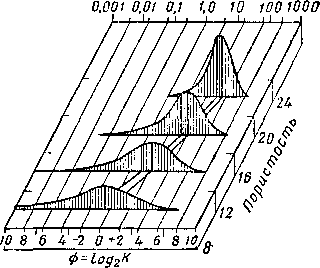
Рис. 11.54. Распределение проницаемости в зависимости от пористости для кернов Вессон [II. 13],
Метод оценки пористости по обломкам породы путем исследования как этих обломков, так и образцов породы был разработан Катцем, Тарнером, Гриммом, Еланбасом
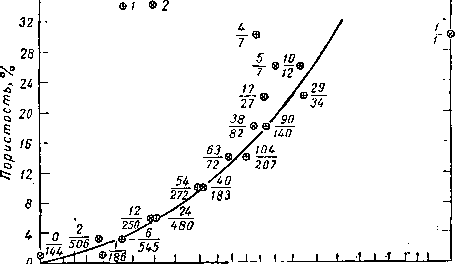
“0,01 0,t / to 2030 SO 60 70 SO 90 99 39,999,99
Содержание керноВ с, проницаемостью,преВышаннцей
Рис. 11.55. Процентное содержание кернов с проницаемостью, превышающей I мд, для доломитизнро-ваиного известняка Фуллертон [II. 13].
/ — вторая зона (1883 анализа кернов); 2—третья зона (13^2 анализа кернов).
С5 Qi | * >* ^
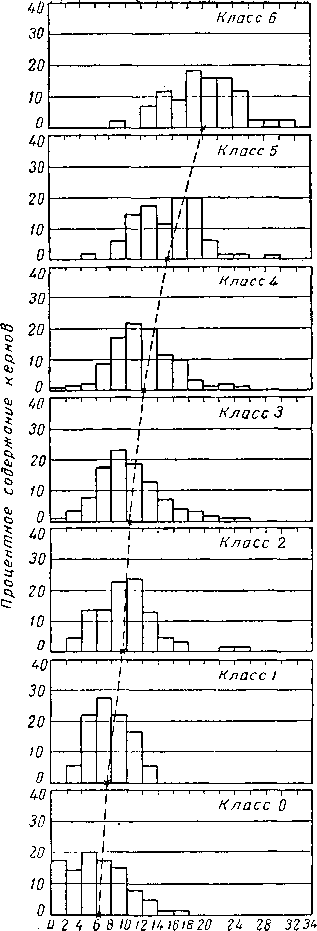
Пористость. %
Рис. 11.57. Распределение пористости кернов по классам [11.36].
Р
С*. * Qj
О 2 4 6 8 W 12 1U /6 18 20 2224- 26 28 30 32 Пористость, %
Ч)
о
5:
Qj
сэ ^ 5: *
1
5: ^
CU 5; хГ СЗ
d *
<3“ qy
Проницаемость, мд 6
Рис. 11.56. Распределение пористости и проницаемости для образцов доломита [11.41].
и Верн [1.36]. Этот метод основан на анализе кер-нового материала нескольких сотен скважин, пробуренных иа доломит Хьюготон. Все керны были разбиты геологами на шесть классов, и каждый керн исследовался с точки зрения его классификации по этой шкале. Для каждого керна были измерены значения пористости и проницаемости, общая закономерность распределения которых показана на рис. 11.56.
Распределение пористости для образцов различных классов приведено на рис. 11.57. Кроме того, был установлен нижний предел проницаемости, .равный 0,03 мд, при котором породу еще можно было считать продуктивной. Далее на диаграммах распределения образцов по пористости для всех типов определены значения нижнего предела пористости, при котором порода была продуктивная. Анализ этих керновых данных позволил пользоваться данными пористости мелких обломков наравне с обычными кернами.
Изучение распределения пор по размерам [II. 12, II. 14] несколько проливает свет на природу пор и их способность содержать промышленную нефть. Интерпретация данных исследования кернов с целью предсказания добычи нефти включает, помимо определения пористости и проницаемости, также и определение их насыщенности [П. 24].
Пористые среды содержат воду (в различной степени минерализованную) независимо от того, присутствуют в них нефть и газ или нет. Наиболее .распространенным компонентом в пластовых водах является хлористый натрий, особенно для пород, отложение которых происходило в морокой воде. Состав первоначальной связанной воды в пористой среде обычно впоследствии изменяется, что вызывается отложением оолей, приносимых грунтовыми водами. Пласты, имеющие непосредственную связь с поверхностью земли, могут содержать пресную воду. Высокоминерализованные пластовые воды приурочены к пластам, залегающим вблизи пород, содержащих растворимые соли [11.66, 11.38]. В табл. [I. 10 приведены результаты анализа вод пласта Ф.рио по данным Джес-сева и Польшаусена [II. 38].
Стифф предложил метод, позволяющий наглядно сравнивать результаты анализа различных вод [11.66]. Метод заключается в нанесении миллиэквивалентов основных ионов, положительных ионов влево, а отрицательных вправо, как показаио на ;рис. 11.58. Сходные по составу воды будут иметь сходные по виду диаграммы, что облегчает их распознавание.
но I5
Со100^
10 »о .
Fl* ь 10
W
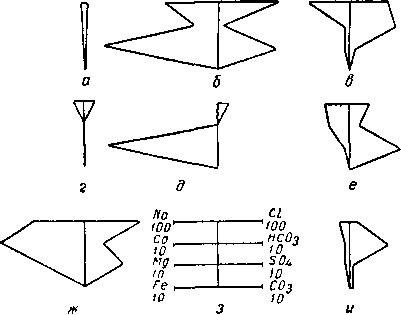
10 15
, сг
'too
не О, 10 J
10 СО.
10
Рис. 11.58. Графическое изображение анализа пластовых вод [11.66].
а — пресная вода; б — морская вода; в — пластовая вода (Вайтмер), промысел Нил, Луизиана; е — пластовая вода (Палакси), промысел Сульфур Блафф, Техас, д — 0,1 н. MgCl2; г —0,1 н. NaC/'. ж — пластовая вода (Арбакл), промысел Блюмер, Канзас;
з —
шкала --------; и — пластовая вода (Лома
Нова), промысел Севен Систерс,
Техас.
Таблица 11.10
Химический анализ вод пласта Фрио
| Кров |
Рассто яние |
Химический | состав. |
% | |||||||
|
Скважина | Месторождение | Глубина, м | ля пласта, м | от кро вли пласта, м | Na + |
Са+ + | Mg+ + |
С1- | so,— |
нсо3~ | С С |
| № 5 Мак-Кинней | Сан....... |
О к р 1258—1260 |
у г С 777 ± | га р р 483 | 1,3802 |
0,1656 | 0,0073 |
2,4244 | 0,0018 |
0,0214 | 1 |
| № I Реквинес | Н. Сан ..... | 1416—1420 |
1037 ± | 383 |
1,3819 | 0,2444 |
0,0058 | 2,5896 |
0,0053 | 0,0116 |
2 |
| № 2 Вила | Бойл...... |
786—790 | 488 ± |
302 | 1,1921 |
0,0344 | 0,0090 |
1,8764 | Нет |
0,0842 | 3 |
| № 1 Хелл Стент | Н. Ринсон .... | 1060—1062 |
702 ± | 362 |
0,7395 | 0,1268 |
0,0050 | 1,2696 |
0,1400 | 0,0110 |
4 |
| № 1 Хелл Стейт | Н. Ринсон .... |
1407—1409 | 702 ± | 707 | 1,0707 |
0,0933 | 0,0078 |
1,7923 | 0,0445 |
0,0078 | 5 |
| № 1 Л. Спир | Развед. скв. . . . | 1648—1658 |
838± | 819 |
1,4249 | 0,1842 |
0,0082 | 2,5049 |
0,0130 | 0,0561 |
6 |
Округ Клиберг
0,0160
0,0111
0,0054
Нет
2,5300
1,4000
1,9000
0,8750
5,4500
0,0201
0,0128
0,0384
0,1068
0,0201
1157
1222
1227
1285
1303
465
209
511
748
594
0,0024
0,0035
0,0010
0,0018
0,0234
1,3756
0,8257
1,0634
0,5809
2,5551
0,2400
0,0738
0,1590
0,0195
0,8168
1591 — 1598 1430
1734—1736
2034
1882—1896
Ранч
9
10
Ранч
Ранч
№ 1 Марк № 3 Кинг Кабеза № 7 Кабеза № 31 Кинг Песо Анчо № 1 Кинг Аррайо
Развед. скв. Силигсон .
Силигсон . Страттон . .
Страттон .
| Кров | Рассто- яние |
Химический | сосга в, |
о/ | |||||||
|
Скважина | Месторождение | Глубина, м | ля пласта, м | от кровли пласта, м |
Na + | Са + + | Mg-!- t- | ci— | so4— |
НС03- | с: с % |
Округ Ньюекс
№ 1 Айсенси № 1 Вебб
I Развед. скв. . [ Флоур Блафф
1820—1824 [1415 2036 1963
410 I 1,94811 0,21481 0,0091 134 I 2,5716| 0,1026 0,0241
I 3,40501 0,00301 0,01401 12 4,1700 0,0020 0,08051 13
Округ Сан Патрицио
1727—1730 |1570±| 160 J 2,9282) 0,2925[ 0,0589 |5,1783| Нет | 0,0148| 14 Округ Рифуджио
№ 2 В. Е. Кирк | Е. Уайт Пойнт . . |
1 О’Коннер
№
№
№
№
№
О’Коннер О’Коннер О’Коннер О'Коннер Грета . .
2 О’Коннер
2 О’Коннер
А—4 О’Коннер
2 Ф. Херд
| 1440 | 1130 + | ЗОЭ | 2,4402 | 0,2345 | 0,0410 | 4,2900 | Нгт | 0,0110 | 13 |
|
1367—1368 | 1130± |
239 | 2,4812 |
0,2022 | 0,0253 |
4,2500 | Следы |
0,0122 | 16 |
| 1523—1528 | 1130± |
399 | 2,5900 |
0,1034 | 0,0115 |
4,2000 | Нет |
0,0256 | 17 |
| 1530 | 1479 ± |
50 | 2,5217 |
0,1454 | 0,0218 |
4,2000 | » |
0,0244 | 18 |
| 1666 | 1365 |
300 | 2,7758 |
0,0626 | 0,0195 |
4,4000 | » |
0,0519 | 19 |
Округ Калхаун
| Из резервуарного парка | Хейсер..... |
1662 Окру |
1585 | 77 г Джексон |
2,4154| 0,0984| 0,0225 | 3,9500 | Нет | | 0,0311 | 20 | |||
| № 1 Иссексон | Разведочная . . . | 1400—1404 |
1390 | 101 |
2,1271 | 0,1832 |
0,0093 | 3,6200 |
Нет | 0,0262 |
21 |
| № 1 Иссексон | Разведочная . . . | 1662—1663 |
1390 | 274 |
1,8229 | 0,1052 |
0,0068 | 3,0000 |
0,0006 | 0,0344 |
22 |
| № 4 М. Браич | Генедо ...... |
2024—2025 | 1539 |
485 | 2,3319 |
0,0652 | 0,0123 |
3,7250 | Нет |
0,0442 | 23 |
| № 1 Спесек | В. Генедо .... | 1668—1675 |
1518 | 159 |
2,3290 | 0,0934 |
0,0232 | 3,8000 |
0,0015 | 0,0488 |
24 |
| № 2 Эдвардс | Маурбро .... | 1592—1595 | 1588 | 11,5 | 2,3616 |
0,1314 | 0,0307 |
3,9500 | Нет |
0,0305 | 25 |
| № В-1 Фор Вей Ранч № А-20 М. Ранч | Н. Ла Ворд . . . |
1594 | 1590 |
5,5 | 2,1598 |
0,1680 | 0,0119 |
3,8000 | » |
0,0183 | 26 |
| Лолита..... |
1950—1951 | 1602 |
349 | 2,5643 |
0,0900 | 0,0173 |
4,1500 | 0,0012 |
0,0293 | 27 |
|
Округ Вартой
№ 5 Кокбарн № 1 Миллер № 1 Из резервуар-ного парка
| Магнет..... |
1688 | 1674 |
14 | 3,0583 |
0,2352 | 0,0376 |
5,2000 | Следы |
0,0817 |
| Луиз...... | 1772—2080 | 1570 | 513 | 1,9957 |
0,0870 | 0,0109 |
3,2400 | » |
0,0390 |
| Пикет Ридж . . . | 1678 | 1617 ± | 61 ± |
2,3100 | 0,2660 |
0,0220 | 4,1000 |
Нет | 0,0290 |
28
29
30
Округ Матагорда
|
№ | Шмидт |
Хамея ..... | 2502 | 2476 | 26 |
3,4965 | 0,4350 |
0,0450 | 6,2800 |
0,0101 | 0,0098 | |
| № | Юнит |
Бакен...... | 2414 | 2350 | 64 ± |
1,9780 | 0,0896 |
0,0174 | 3,1636 |
0,0050 | 0,1647 | |
| Лаки...... |
2608- | -2610 |
2409 | 201 |
1,6968 | 0,0244 |
0,0059 | 2,6053 |
0,0051 | 0,1198 | ||
| Лаки...... |
2722- | -2723 |
2409 | 313 |
0,4616 | 0,0064 |
0,0028 | 0,6560 |
0,0112 | 0,1159 | ||
| Лаки...... |
2866- | -2867 |
2409 | 397 |
0,6424 | 0,0052 |
0,0051 | 0,9042 |
0,0066 | 0,1824 |
||
31
32
33
34
35
Округ Бразория
№ 1 Д. О. Эванс № 1 Мак Кинней № 1 Д. В. Рейнольдс
| Олд Оушен . . . |
3080-3085 | •2683 ± |
402 | — |
— | — |
1,4600 | — |
— |
| Олд Оушен . . . | 3085—3090 |
— | 408 |
— | — |
— | 1,8100 |
— | — |
|
Олд Оушен . . . |
3080—3086 | _ |
403 | 1,0750 |
0,0333 | 0,0021 |
1,6450 | Следы |
0,1348 |
| Олд Оушен . . . | 2963—2967 | 2683 ± | 284 |
1,0779 | 0,0098 |
0,0021 | 1,5769 |
0,0060 | 0,1815 |
| Олд Оушен . . . |
3088—3091 | 409 |
1,4155 | 0,0137 |
0,0064 | 2,1276 |
0,0151 | 0,1507 | |
| Олд Оушен . . . |
3068—3092 | 410 |
0,7180 | 0,0024 |
0,0017 | 0,9928 |
0,0256 | 0,1808 | |
| Чоколейт Байоу . |
3480 | 2700 |
780 | 2,9170 |
0,2244 | 0,0360 |
4,9951 | 0,0037 |
0,0580 |
| Денбари .... | 2015—2020 |
1989 ± | 31± |
1,6625 | 0,0638 |
0,0112 | 2,6500 |
0,0075 | 0,0976 |
| Денбари .... | 1730 | 1708 ± | 22± |
2,7400 | 0,1104 |
0,002,) | 4,3800 |
Нет | 0,0921 |
| Англетон .... |
3227—3229 | 2714 + |
482 | 1,7581 |
0,1688 | 0,0063 |
2,9800 | д |
0,0854 |
| Хастингс .... | 1867 |
1757 | 110 |
3,8852 | 0,1804 |
0,0322 | 6,4000 |
» | 0,0183 |
| Пледжер..... | 2073 ± | 2000 | 46 ± | 0,6890 | 0,0253 | 0,0072 | 1,0900 | » | 0,0665 |
| Сенди Пойнт . . . |
198.1—1981 | 1972 |
9 | 3,6262 |
0,1808 | 0,0338 |
5,9927 | 0,0069 |
0,0244 |
| Сенди Пойнт. . . | 1978—1982 |
1972 | 10 |
3,8899 | 0,2005 |
0,0363 | 6,4537 |
0,0037 | 0,0104 |
Примечание. Данные взяты кз
36
37
38
39
40
41
42
43
44
45
46
47
48
49
№ 1 Андреу № С-1 Блекли № В-1 Моллер № 1 Меттлер № 16 С. Браун . . № 1 М. Мак Фар-ленл
