Глава 13. эксплуатационные расчеты лопастных насосов
Глава 13. ЭКСПЛУАТАЦИОННЫЕ РАСЧЕТЫ ЛОПАСТНЫХ НАСОСОВ
2.9. Методы теории подобна в лопастных насосах
Теория подобия имеет большое значение при проектировании и экспериментальном исслсдовапип лопастных васосов. Теория подобия дает возможность по известной характеристике одного пасоса получить характеристику другого, если проточные полости обоих насосов геометрически подобии, а также пересчитать характеристику иасоса с одной частоты вращения на другую. Это облегчает экспериментальное исследование лопастного насоса, давая возможность получить характеристику мощного натурного насоса сутей испытания его уменьшенной модели или же испытывать натурный пасос на частоте вращения, отличающейся от той частоты вращения, па которой насос эксплуатируется.
Используя теорию подобия можно выбрать модельный насос, проточная полость которого геометрически подобна полости проектируемого пасоса (натурного), рассчитать соотношения размеров этих насосов и, следовательно, получить размеры рабочих органов проектируемого насоса. Пересчитав по теории подобия характеристику модельпого иасоса, можпо получить характеристику проектируемого ьасоса. Такой способ проектирования насоса широко применяется.
Приведенные ниже формулы пересчета параметров насоса справедливы при соблюдении следующих условий.
1. Геометрическое подобие проточных полостей пасоса, включающее также подобие шероховатостей поверхности стенок внутренних каналов, зазоров в щелевых уплотнениях и толщин лопаток рабочего колеса.

2. Кинематическое подобие на границах потоков. Границами потока являются, в частности, его сечсние у входа в насос и движущиеся лопатки колеса. Для выполнения условий кинематического подобия на границах потоков необходимо, чтобы средн^ скорость жидкости ув-, у входа в пасос была пропорциональна окружной скорости рабочего колеса и\
t»BX с\э и = лОп/бО tv nL,
гдо п — частота вращении рабочего колеса; L — характерный размер пасоса, например диаметр колеса.
Подача насоса равна произведению скорости vhX на площадь нормального сечения потока у входа в иасос, которая пропорциональна линейному размеру L во второй степени. Отсюда Q лг vBXL2 ^5 nL3, шла
![]()
(2.33)
где ипдексом 1 обозначены величины для первого насоса, индексом 2 — для второго пасоса, геометрически подобного первому.
3. Динамическое подобие потоков. Динамическое подобие напорных установившихся потоков требует равенства Re, которое у лопастных насосов обычно принимают равным UjDj/m.
Следствием выполнения этих условии являются:
1) кинематическое подобие во всех точках потоков; при отом лгобыо скорости жидкости
2) равенство числа Эйлера Ей, которое для напорного движения равно gAHcriu2 и, следовательно, пропорциональность -разности статических напоров ДЛГСТ скорости жидкости во второй степени п ilg.
Режимы работы насоса, при которых выполняются описанные условия, называются подобными.
Теория подобия позволяет установить формулы пересчета параметров лопастных насосов, определяющие зависимость подачи, папора, моментов сил и мощности геометрически подобных насосов, работающих па подобных режимах, от их размеров и частоты вращения.
Подача насоса пересчитывается по уравнению (2.33).
Напор насоса согласно уравнению (2.1)
Я = ДЯсг + Д^/(2.?),
где Д И а = г« — га + (рп — Рв)/( PS) и 4^/(2 g) — разность соответственно ста-Точсских и скоростных напоров поели пасоса и до него.
Эти разности напоров пропорциональны скорости жидкости во второй степепи и l/jj
ДЯст vi!g\ Ду2/<2 g) со v'ig,
поэтому напор пасоса
Я оо i2lg.
Припимая gi = и учитывая уравнение (2.34), получаем
Момент сил взаимодействия потока со стенками каналов М с\з счз pi^L3 (см. п. 1.20). Отсюда получим формулу пересчета момента сил
(2.36)
Мощность, передаваемая от вала па рабочее колесо,
» аМву
где Д/„ — момент сел, с которым жидкость действует ва рабочее колесо (в том числе сил дисковой» трс-ппя).
Учитывая уравнение (2.36), находим JVacvpn3Z5. (2.37)
Мощность насоса превышает мощность ЛГ„ на велочипу мощпости» расходуемой на трение в уплотнении нала о подшипниках. Эта мощность но уравнению (2.37) не пересчитывается. Однако если насос не слишком мал, то потери на трепио в уплотнениях вала н н подшипниках малы и для приближенного пересчета мощности насоса можно применять уравнение (2.37). Следовательно,
![]()
(2.38)
При соблюдении всех условий подобия расход в щелевых уплотнениях насоса пропорционален его подаче, гидравлические потери в насосе, которые для подобных режимов пронорциопальны скорости жидкости во второй степени, пропорциональны напору насоса, дисковые потери мощности пронорциопальны мощности NB. Отсюда на основании уравнении (2.10), (2.11) н (2.7) следует равенство для подобных режимов объемного и гидравлического КПД и приближенное равенство механического КПД:
*1о1 —Л02! Лмех 1 ^ Лм« 2! tli^ Ла- (2 39)
Приведенный выше пыиод формул пересчета пе связан с особенностями рабочего процесса лопастного пасоса, поэтому формулы справедлива не только для лопастных насосов, но и для других видов гид-ромапшп (в том числе двигателей), имеющих вращающиеся рабочие органы или цикличный рабочий процесс.
Геометрическое подобие щелевых уплотнений, шероховатости стенок и толщины лопаток не всегда выполняется. Обычно у более крупных насосов зазоры в уплотнениях, шероховатость и толщина лопаток относительно меньше, чем у малых. Равенство Ие для модели и натуры также не всегда удается выполнить. Однако если эти отклонения от подобия невелики, то формулы (2.33), (2.35), (2.36), (2.38) и
(2.39) дают достаточпо точные результаты. *
Формулы пересчета для одного и того же насоса, работающего на разных частотах вращения {Ls — L2), принимают вид:
QifQi = nt/n2', (2,40)
(2.41)
(2.42)
Н1/Нг = (п1/п.г)2;
Так как обычно при изменении частоты вращения насоса равенство Re пе выдерживается, то формула (2.41) дает приближенный результат. По этой же причине, а также потому, что мощность трения в подшипниках и уплотнениях вала по уравнению (2,42) пе пересчитывается, формула (2.42) также приближенна. Опыты показывают, что формула (2.41) является более точной; при достаточпо больших значениях Re = toi?|/v > Ю6 ее можно применять даже в том случае, если частоты вращения значительно различаются.
2.10. Пересчет характеристик лопастных насосов на другую частоту вращепия
Предположим, что имеется характеристика насоса при частоте вращения гаь а двигатель этого насоса работает при частоте вращения п2, отличной от Bi. Для того чтобы судить об эксплуатационных свойствах насоса, необходимо иметь его характеристику при той частоте вращения и,, при которой он фактически будет работать.
Эту характеристику можно получить путем пересчета имеющейся характеристики на новую частоту вращения ка до формулам
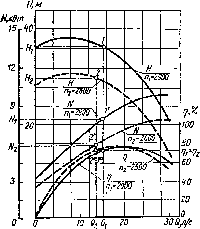
(2.40)—(2.42) и (2.39). Для этого задаются рядом значений подач <?, и но имеющейся характеристике насоса находят соответствующие им папор Нъ мощность и КПД T|i (рис. 2.21). Подставив найденные для частот вращения гс, величины Qu II v А', и г]г в уравпения (2.40)—
(2.42) и (2.39), получают значения подачп Qt, напора Нг, мощности Л~2 и КПД т)2, которые являются координатами точек Рис. 2.21. Пересчет характеристика иасоса характеристики насоса ва другую частоту вращении прк частоте вращения н%.
По этим координатам строят на характеристике ряд точек, соединив которые плавными кривыми, получают искомую характеристику насоса при частоте вращения м2.
Найдем в координатах Q — Я геометрическое место точек режимов, подобных режиму, который определяется точкой 1 (рис. 2.22). Для этого, подставив координаты Q1 и И г точки 1 в уравнения (2.40) и (2.41),.определим напор и подачу при различных значениях частоты вращения. В результате найдем ряд точек' 2, 3, 4, ..., соединив которые плавной линией, получим кривую подобных режимов работы насоса. Покажем, что эта кривая представляет квадратичную параболу с вершиной в начале координат. Для этого подставим в уравнение (2.41) значения Пд/л2, найденные из уравнения (2.40),
Hi/Qi — HilQl — Нз/Ql — ¦¦¦ = Я/Q2 = const — s.
Следовательно, уравнение кривой подобных режимов имеет вид
(2.43)
Для подобных режимов гидравлический и объемный КПД с достаточной степенью точности можно считать одинаковыми. Слодовательпи, кривые подобных режимов являются также кривыми равных обгемвых и гидравлических КПД насоса. Механический КПД для подобных режимов не остается постоянным, поскольку механические потери складываются из потерь как на дисковод трение, так и на трение в уплотнениях вала ы иодшпнншгах. При возрастании частоты вращении мощность дискового трения увеличивается пропорционально гидравлической мощности (или частоте вращения в третьей степени), потери ж о на трение в j. гглотненпях вала и подшипниках растут значительно медленнее, чем птдранлпческая мощность. В результате при увеличении частоты вращения роль потирь на трение в уплотнениях пала и подшипниках в балансе энергии уменьшается, что приводит к увеличению механического и, следовательно, общего КПД.
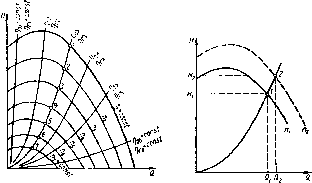
Рис. 2.22. Кривые подобных режи- Рис. 2.23. К определению час-
тоты вращения, при которой характеристика прохЛпт через заданную режимную точку
Предположим, что от насоса требуется получить подачу Q2 при шпоре Нг и что режимная точка 2 с координатами Q.z и //2 не лежит на характеристике насоса, полученной при частоте вращения nL {рис. 2.23). Надо определить такую частоту вращения, при которой пасос сможет обеспечить заданный режим работы, другими словами, определить такую частоту вращения пг, при которой кривая напоров Н = { (Q) характеристика пройдет через заданную точку 2 с координатами Q2 и И3.
Искомую частоту вращения п2 можно определить, используя формулы (2.40) и (2.41) пересчета. Поскольку они справедливы только для подобных режимов, то для того чтобы можно было ими воспользоваться, необходимо найти такой режим (<?,, Нх) работы насоса при частоте вращения щ, который был бы подобен заданному режиму (С?2> Нг)' Выше было показано, что подобные режимы работы насоса лежат на параболе подобных режимов Н = sQ2. Этому уравнению должны удовлетворять координаты заданной точки 2 и искомой точки
1. Положение точки 1 паходим графическим путем. Для этого проводим через задацную точку 2 параболу подобных режимов. Пересечение параболы с кривой напоров Н — f (Q) при частоте вращения дает режимную точку 1 с координатами Q1 и //,. Так как точки 1 и 2 лежат на одной и той же параболе подобных режимов, то режимы
1 и 2 подобны и для них справедливы формулы
я1/я2 = (п1/п2)а.
В этих формулах неизвестна только частота вращепия щ, которую можно определить по любому из уравнений.

2.11. Коэффициент быстроходности
Выше было указано, что в настоящее время широко применяется проектирование оового насоса путем пересчета по формулам подобия размеров существующего насоса. Для того чтобы воспользоваться этим методом, следует выбрать срсди всего многообразия существующих насосов, имеющих высокие техппко-экономические показатели, такой насос, у которого режим, подобный заданному режиму работы проектируемого насоса, был бы близок к оптимальному. Для этого необходимо найти параметр, который служил бы критерием подобия
и, следовательно, был бы одинаков для всех подобных насосов. Определив по заданным Я, Q и и проектируемого насоса этот критерий подобия и сравнив его с критериями подобия имеющихся конструкций, получим возможность подобрать необходимый насос.
В предыдущем параграфе было выяснено, что для подобных насосов, работающих на подобных режимах, справедливы уравнения
QijQi = (n1jnt)(L1jL,'p и BjjBa = [nlLil(ntL3)]\
Эти уравнения можно записать иначе:
QiHnitT) = (?a/{«a-?0 = <?/{«i3) = <}] (2.44)
#i/<ni?i)2 -= Нг!(пъЬ о)2 -- НЦпЬ)2 = /г. (2.45)
Величины q и h одинаковы для подобных насосов, работающих в подобных режимах, и, следовательно, являются критериями подобия. Однако они не могут быть определены для проектируемого насоса, так как неизвестен его размер L.
Для того чтобы исключить из уравнений (2.44) и (2.45) линейный размер L, возведем правую и левую части уравнения (2.44) во вторую степень, а уравнения (2.45) — в третью и разделим уравнения одно на другое:
фпЧ'ЛГРп*#) = п4<?*/Я3= qt/h3, или
Как параметры д в h, так и пу одинаковы для геометрически подобных насосов при работе их еа подобных режимах независимо от плотности перемещаемой жидкости. Следовательно, параметр п7 является искомым критерием подобия. Его можно назвать удельной частотой вращения.
В иасосостроенип большее распространение получил параметр п3, называемой коэффициентом быстроходности и в 3,65 раза больший удельной частоты вращения:
Коэффициент 3,65 пе изменяот физического смысла п5, который, так же как и пу, является критерием (признаком) подобия насосов. Его происхождение историческое.
Входящие в уравнения (2.46) и (2.47) величины имеют следующие размерности: Q в м®/с, Я в м, в в об/мин.
Если пасос, геометрически подобный данпому, при подяте Q = 0,075 м3/с имеет напор 1 и, то согласно уравнению (2.>57) ого коэффициент быстроходности па равен частоте вращения иасоса. Дейстицтельпо
3,65л У"(Щ75 ”« ге'
Па этом основании часто коэффициентом быстроходности называют частоту вращения насоса, геометрически подобного данному, который при напора 1 ц подаст 0,075 м3/с жидкости.
Коэффициент быстроходности различен для разных режимов работы насоса. Назовем коэффициент быстроходности, определенный для оптимального режима, т. с. для режима, соответствующего максимальному значению КПД, коэффициентом быстроходности насоса. Если насосы геометрически подобны, то коэффициенш быстроходности у них одинаковы. Следовательно, рлвснство коэффициентов быстроходности является необходимым признаком подобия насосов. Поскольку ва заданные значения параметров п, Q0I1T и Яопт и, следовательно, дли заданного зпачения коэффициента ^строход-ности можно сконструировать насосы с разными соотношениями размеров, равенство коэффициентов быстроходности пе является достаточным признаком геометрического подобия пасосов. Однако практикой установлены для каждого коэффициента быстроходности соотношения размеров насоса, обеспечивающие оптимальные технико-экопомнческие показатели. Если ограничиться лишь этими, чаще всего применяющимися в насосах соотношениями размеров, то равенство коэффициентов быстроходности становится не только необходимым, но и в известной степени достаточным признаком (критерием) геометрического подобия насосов.
В зависимости от коэффициента быстроходности рабочие колеси лопастных насосов можно разделить на следующие разновидности (табл. 2.1).
1. Центробежные. Центробежные насосы бывают тихоходными а нормальными. Тихоходные пасосы имеют малый коэффициент быстроходности (ns — 50 90). Из уравнения (2.47) слодует,
Таблица 2.1

-2Г а
s*a ©
I
что прв постоянной подаче и частоте вращения (чему соответствует постояпный диаметр горловины рабочего колеса i>0) коэффициент быстроходности тем меньше, чем больше напор. Чтобы получить большой напор, необходимо иметь большой диаметр Ds рабочего колеса, поэтому тихоходные рабочие колеса имеют большое отношение D2/D0 диаметров, доходящее до трех. Лопатки рабочего колеса обычно имеют простую цилиндрическую форму с образующей цилиндра, параллельной оси иасоса.
Нормальными являются колеса, имеющие п3 = 80 ¦+¦ -г- 300. Увеличение быстроходности, связанное с уменьшением па-пора, ведет к уменьшению выходного диаметра рабочего колеса (i>2/i>0 = 2,5 1,4). Для уменьшения гидравлических потерь на
входе в рабочее колесо, значение которых в общем балансе энергии возрастает по мере уменьшения напора насоса, входной участок лопаток выполняется двойной кривизны. Выходной участок имеет дилнндрическую форму.
2. Полуосевяе (в3 — 250 + 500; D2/D0 = 1,4 + 0,9). Уменьшить отношение Dt/D0 до значения, близкого или меньшего единицы, можно только в том случае, если выходную кромку лопаток наклонить к оси. Кроме того, наклон выходной кромки обеспечивает более плавную форму лопатки, что уменьшает гидравлические потери в рабочем колесе. Чтобы получить на разных струйках, имеющих разный диаметр выхода, одинаковый напор, приходится лопатку выполнять двойной кривизны не только па входе, но и на выходе.
3. Осевые, или пропеллерные (пе - 500 -*¦ 1000; D^/D0 г» 0,8). При дальнейшем увеличении быстроходности наклон выходной кромки лопаток возрастает, и она становится почти перпендикулярной к оси насоса. При этом частицы жидкости движутся через рабочее колесо приблизительно ыа постоянном расстоянии от его оси. В отличив от большинства центробежных насосов колесо осевого насоса не имеет наружного обода.

В табл. 2.1 приведены также характеристики лопастных насосов. По мере увеличения коэффициента быстроходности кривая напоров U = / (ф) становится более крутой. Мощность при иодач!, равной пулю, увеличивается с ростом быстроходности. Бели у насосов с тихоходными и нормальными колесами мощность возрастает с увеличением подачи, то у насосов с полуосевымп колесами она почти не изменяется с изменением подачи, а у насосов с осевыми колесами с увеличением подачи уменьшается. Чем больше коэффициент быстроходности, тем круче падает кривая КПД по обе стороны от оптимального режима и, следовательно, тем меньше стаповится диапазон подач, в котором работа насоса экономически выгодпа. Однако из-за увеличения крутваны кривой напоров характеристики диапазон оптимальных напоров при увеличении быстроходности возрастает.
Так как папор лопастного насоса не зависит от рода перекачиваемой жидкости (см. п. 2.6), удельная частота вращепия и коэффициент быстроходности также не зависят от рода жидкости.
Многоступенчатый насос представляет собой несколько последовательно соедипегатых одноступенчатых насосов (ступеней), поэтому для него принято определять коэффициент быстроходности ступени, а не всего насоса, для чего в уравнения (2.46) и (2.47) следует подставлять напор одной ступени.
Рабочее колесо насоса двустороннего входа можно рассматривать как два параллельно соединенных колеса, поэтому при определении коэффициента быстроходности такого насоса значение подачи, входящее в уравнения (2.46) и (2.47), следует брать равным Qf2, где Q — подача насоса.
2.12. Расширение области применения
центробежных насосов обточкой рабочих колес
Предположим, что от насоса требуется получить подачу Q' и напор Н' и режимная точка А с координатами Q' и И' лежит ниже характеристики пасоса (рис. 2.24). Пусть двигатель насоса не имеет регулировки частоты вращения (например, асинхронный двигатель с короткозамкнутым ротором). Для того чтобы работа насоса соответствовала режимной точке А, следует так изменить его характеристику, чтобы она прошла через эту точку. Если нельзя решить эту задачу изменением частоты вращения пасоса, то применяют обточку рабочего колеса но наружному диаметру. При уменьшении наружного диаметра рабочего колеса 02 окружная скорость щ па выходе из колеса уменьшается, что ведет к уменьшению напора. Следовательно, при обточке колеса кривая характеристики насоса понижается и при некотором значении Dt пройдет через заданную режимную точку.
/ /
Рис. 2.24. 11араболл обточек
Опыты показывают, что для расчета характеристики центробежного насоса, получающейся после обточки его рабочего колеса, можно приближенно принять пропорциональность подачи первой степени, а напора второй степени наружного диаметра рабочего колеса:
Q)Q' = Яа/Я*; (2.48) II/II' = (Di/Di)2. (2.49)
Эти зависимости получены эмпирически. Опыты показывают также, что для режимов, удовлетворяющих уравнениям (2.48) и
(2.49) КПД насоса приблизительно одинаков, если обточка рабочего колеса не слишком велика.
Подставив в уравнение (2.49) отношевие D^/Dq, найденное из уравнения (2.48), получим
Hfll' — (Q(Q')2 или HjQ1 = H'KQ'f = coast = с,
откуда
Следовательно, режимы, удовлетворяющие уравнениям (2.48) и
(2.49), располагаются в поле Н — Q на параболо, имеющей вершину в начале координат. Будем называть эту параболу параболой обточек. При обточке рабочего колеса по наружному диаметру геометрическое подобие нарушается, поэтому парабола обточок не имеет ничего общего с параболой подобных режимов.
Определим, до какого диаметра необходимо обточить рабочее колесо, чтобы характеристика насоса прошла через режимную точку с координатами Q' и Н'. Проведем через эту точку параболу обточек (см. рис. 2.24). На пересечении этой параболы с характеристикой насоса находим режимную точку В с координатами Q и Н. Для точек Л и В справедливы уравнения (2.48) и (2.49). Подставив в любое из этих уравнений координаты точек Л и В и зная диаметр D2 рабочего колеса до обточки, определяем диаметр D“t обточенного колеса.
При больших обточках рабочего колеса КПД насоса уменьшается, что ограничивает обточку. Предельная величина обточки рабочего колеса зависит от коэффициента быстроходпости ns.
200
0,11
300
0,09
350
0,07
0,20
(Dj—D’)/Da
Насос выгодно эксплуатировать только в области высоких КПД и больших высот всасывания [малых кавитационных запасов (см. п. 2.19)], поэтому должна использоваться не вся характеристика па-соса, а только часть ее. Минимальная подача рабочего участка характеристики пасоса определяется допустимым снижением КПД по сравнению с максимальным; максимальная подача — допустимым снижением КПД или, чаще, допустимым повышением кавитационного запаса, который при подачах, больших оптимальной, резко возрастает (см. рис. 2.15). Пусть кривая 1 па рис.
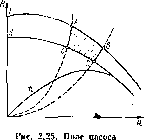
2.25 является характеристикой насоса с необточенным колесом. Участок АВ характеристики является рабочим. Построим характеристику насоса при максимальной обточке рабочего колеса (кривая II) и нанесем на пей границы С и D рабочего участка. Соединив точки А и С, а также точки В и D, получим четырехугольник ABDC. Все режимные точки четырехугольника молено получить, применяя промежуточную обточку рабочего колоса. Режимы, лежащие в пределах четырехугольника, удовлетворяют требованиям, предъявляемым как по значению КПД, так и по высотам всасываиия и, следовательно, являются рабочими. Четырехугольник ABDC называется полем насоса.
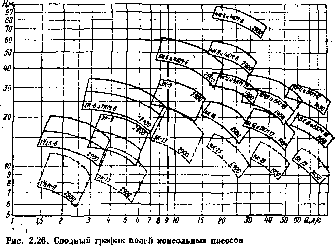
На рис. 2.26 изображен сводный график полей консольных насосов, построенный в логарифмических координатах. Такие трафики прилагаются к каталогам насосов, выпускаемым промышлен-ностыо, и облегчают выбор насоса (но заданным значениям подачи и напора находят на сводном графике режимную точку и соответствующую ей марку в частоту вращения насоса).
2.13. Насосная установка и ее характеристика
На рос. 2.27 изображена схема насосной установки. К насосу 7, приводимому от электродвигателя 6, жидкость поступает из приемного резервуара 1 по подводящему трубопроводу 12. Насос нагнетает жидкость в напорный резервуар 2 по напорному трубопроводу • 3. На напорном трубопроводе имеется регулирующая задвижка 8, при помощи которой изменяется подача насоса. Иногда на напорном трубопроводе устанавливают обратный кланан 10, автоматически перекрывающий напорный трубопровод при остановке пасоса и препятствующий благодаря этому возникновению обратного тока жидкости из напорного резервуара. Если давление в приемном резервуаре отличается от атмосферного или насос расположен ниже уровня жидкости в приемном резервуаре, то на подводящем трубопроводе устанавливают монтажную задвижку 11, которую перекрывают при остановке или ремонте насоса. В начале подводящего трубопровода часто предусматривают приемную сетку 13, предохраняющую насос от попадания твердых тел, и пятовой клапан 14, дающий возможность залить насос н подводящий трубопровод жидкостью перед пуском. Работа насоса контролируется по расходомеру 4, который измеряет подачу насоса, по манометру 5 и вакуумметру или манометру 9, дающим возможность определить напор насоса.
Назовем уровни свободной поверхности жидкости в приемном и напорном резервуаре приемным и напорным уровнями-, разность Яг высот напорного и проемного уровней — геометрическим напором насосной установки.
Для того чтобы перемещать жидкость по трубопроводам установки из приемного резервуара в напорный, необходимо затрачивать энергию на подъем жидкости на высоту Нс, па преодоление разности давлений р’ — р' в резервуарах и на преодоление суммарных гидравлических потерь 2АИ всасывающего и напорного трубопроводов. Таким
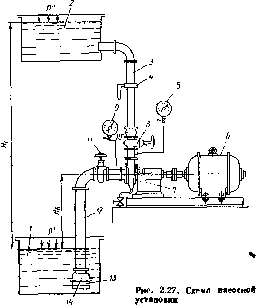
образом, энергия, необходимая для перемещения единицы веса жидкости из приемного резервуара в напорный по трубопроводам установки, ели потребный напор установки..
я„01Р=яг + г^?1+2:*ц=ли+2*„ (2.51)
где Яст = //г + (р" ~ p')/(pg) ~ статический напор установки.
Характеристикой насосной установки называется зависимость потребного напора от расхода жидкости. Геометрический напор Яг, давления р" и р' и, следовательно, статический напор Яст от расхода обычно не зависят. При турбулентном режиме гидравлические потери пропорциональны расходу во второй степени:
где к — сопротивление трубопроводов пасосной установки.
На рис. 2.28 справа изображена характеристика насосной установки, слева — схема установки. Уровни, па которых размещены элементы установки, на схеме вычерчены в масштабе оси напоров графика. Уровень в приемном резервуаре совмещен с осью абсцисс. Так как статический напор установки от подачи насоса ые зависит, характеристика пасоспой установки представляет суммарную характеристику подводящего и напорного трубопроводов 2йп = kQ'!, смещенную вдоль осп напоров на величину Пст.
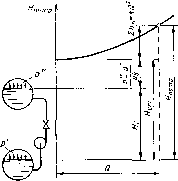
3 Рис. 2.28. Характеристика насосной установки
2.14. Работа насоса на сеть
Насос данной насосной установки работает на таком режиме, при котором потребный напор равен напору насоса, т. е. при котором энергия, потребляемая при движении жидкости по трубопроводам установки (потребный напор) равна энергии, сообщаемой жидкости насосом (напор насоса).
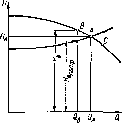
Рие. 2.29. Определение режима работы насос» на сеть
Для определения режима работы насоса следует па одном и том же графике в одинаковых масштабах нанести характеристику пасоса и пасосной установки (рис. 2.29). Равенство напора иасоса г, потребного напора установки получается для режима, определяемого точкой Л пересечении характеристик. Покажем, что пасос не может работать в режиме, отличном от режима А. Предположим, что насос работает в режиме В. В этом случае папор, сообщаемый насосом жидкости, равеи Нв движении жидкости но трубопроводам установки, И в потр</^в- Таким образом, энергия, расходуемая при движении жидкости по трубопроводам установки, меньше энергии, сообщаемой ей насосом. Избыток энергии в жидкости идет на приращение ее кинетической энергии. Следовательно, скорость жидкости увеличивается. Увеличение скорости приводит к увеличению расхода, которое будет происходить до тех пор, пока он сравняется с Qa• Если подача насоса больше Qa (точка С), то сообщаемый насосом напор мепьше потребляемого. Недостаток энергии восполняется за счет собственной кинетической энергии жидкости. Это приводит к уменьшению скорости движения
, папор, расходуемый при
и, следовательно, к уменьшению расхода до Qa-
Рассмотрим частные случаи насосных установок.
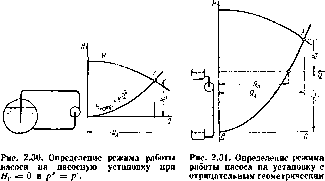
1. Приемный и напорный уровни совпадают. При этом геометрический напор установки Нт = 0, р’ — р' и характеристика насосной
напором
установки представляет собой кривую Наотр = kQ2 (рис. ^30). Весь напор затрачивается на преодоление гидравлического сопротивления в системе. Наносим на характеристику установки характеристику насоса. Пересечение кривой напоров И = / (Q) пасоса с характеристикой установки Яп01р = / (Q) дает рабочую точку А, определяющую режим работы насоса.
2. Напорный уровень находится ниже приемного (рис. 2.31). Геометрический напор при этом отрицателен, поэтому его следует откладывать впиз от оси абсцисс графика. Пусть р’ = р'. Приемный уровень схемы установки совмещаем с осью абсцисс. Построив от прямой ВС вверх кривую потерь = kQ2, получим характеристику установки. На пересечении кривой папоров характеристики насоса с характеристикой насосной установки находим точку А, которая определяет режим работы насоса. Точка пересечения характеристики установки с осью абсцисс дает расход Q0 в трубопроводе при отсутствии насоса. Включение пасоса увеличило расход в системе на величину Qa — Qo-
2.15. Неустойчивая работа насосвон установка (понпаж)
В некоторых случаях работа насоса является неустойчивой: подача резко изменяется от наибольшего значения до нуля, напор колеблется в значительных пределах, наблюдаются гидравлические удары, шум и сотрясения всей машины в трубопроводов. Это явление называется помпажем. Помпаж происходит у насосов, имеющих кривую напоров Н = /(<?) с 8ападающей левой ветвью (рис. 2.32), т. е. кривую напоров, имеющую максимум при Q > 0. Такую характеристику имеют обычно тихоходные насосы.
Рассмотрим неустойчивую работу Bc.toca по схеме, изображенной на рис. 2.32. Насос 1 подает жидкость по трубопроводу S в резервуар 5, откуда она поступает по трубе 4 к потребителю. Пусть в начальный момент резервуар заполнен жидкостью до уровня а. Прп этом насос работает в режиме, определяемом точкой А. Если расход жидкости, отводимый к потребителю, меньше подачи насоса QA, то уровень жидкости в резервуаре повышается, характериствка установки смещается вверх и подача насоса в соответствии с кривой напоров U = f (Q) уменьшается до тех пор, пока рабочая точка не займет положения М. Если при этом подача насоса превышает расход, который сбрасывается из резервуара 5 по трубе 4, то уровень в резервуаре повысится ещо больше и характеристика установки пройдет выше характеристики насоса. При этом потребный напор Станет больше напора насоса, в результате чего произойдет срыв подачи. Под действием обратного тока жидкости обратный клапан 2 закроется. Насос будет работать при подаче Q = 0 и напоре Нв. Из-за отсутствия притока жидкости в резервуар 5 уровень жидкости в нем будет понижаться (жидкость продолжает вытекать из резервуара 5 по трубе 4). После того как уровень понизится до высоты, соответствующей напору Н0, насос снова вступит в работу. Подача резко, скачкообразно, возрастет до Qb, соответствующей рабочей точке В. Уровень в резервуаре опять начнет постепенво подниматься и явление повторится.
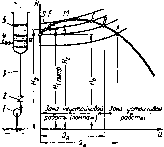
Рве. 2.32. К определению зоны нв-
Срыв подачи насоса и переход его на холостой режим работы могут получиться и при неизменной характеристние установки (уровень в резервуаре 5 постоянен), если характеристика установки пересекает характеристику насоса в двух точках (точки С и D характеристики). Это может возникнуть при снижении частоты вращения (например, из-за временного падения напряжения электросети, цнта-ющеЙ двигатель). Прн этом характеристика насоса понизится и произойдет срыв подачи до нуля. При последующей повышении частоты вращения насос будет продолжать работать ори холостом режиме (Q =s 0), так как напор, создаваемый им при Q = 0, меньше статического напора установки. По этой же причине помпаж может возникнуть при параллельной работе насосов, если напор при нулевой подаче одного из насосов меньше напора второго насоса при его одиночной работе на сеть (например, если на рис. 2.38 II01 ¦< Нр). В этом случае временное снижение частоты вращения насосов может привести к срыву подачи первого насоса до нуля.
Покажем, что насос вс. может работать в режимах, расположенных левее точки М касания характеристики насоса и насосной установки (см, рис. 2.52). Пусть режим работы насоса отклонится от режима, характеризуемого точкой D, в сторону больших подач (точка Е). При этом потребный напор НЕ потр меньше напора сообщаемого жидкости насосом (Я Е потр < #/,;)• В жидкости имеется избыток эвергви, который идет ва приращение ее кинетической энергии. При этом скорость жидкости увеличивается до тех пор, пона расход не достигнет значения, соответствующего режимной точке С. При отклонении режима насоса от режима, характеризуемого топкой D, в сторону меньших подач потреопьгп ва-1юр больше напора насоса. Недостаток энергии в жидкости приведет к ее замедлению и, следовательно, к падению подачи до пуля. Таким обрапом, ори отклонении режима работы насоса от равновесного резкпма (точка D) он не возвращается в первоначальное положение. Следовательно, режимы работы насоса, лежащие левее тотки М, неустойчивы. Такпи же способом можно показать, что режимы, расположенные правее точки М, являются устойчивыми и насос в них может работать. Режимы, расположенные между точками М и В, опасны в связи с возможностью возникновения помиажа, так как при этих ре* жимах характеристика устяпоски пересекает характеристику пасоса в двух точках, поэтому границей устойчивых режимов является точка Вх а не точка М'
Характеристики насосов, не имеющих неустойчивой области, на-зывают стабильными. Насосы, применяемые для подачи жидкости прн переменных режимах, должны иметь стабильные характеристики.
2.16. Регулирование режима работы насоса

Данной характеристике насоса и насоспой установки соответствует только одна рабочая точка. Между тем, требуемая подача может изменяться. Для того чтобы изменить режим работы насоса, необходимо изменять характеристику насоса либо насосвой установки. Это изменение характеристик для обеспечения требуемой подачи называется регулированием. Регулирование центробежных и малых осевых насосов может осуществляться либо при помощи регулирующей задвижки (изменяется характеристика насоспой установки) или изменением частоты вращения (изменяется характеристика пасоса). Иногда малые осевые насосы регулируют перепуском части расхода из напорного трубопровода во всасывающий. Работа установки со средними и крупными осевыми насосами, имеющими поворотные лопасти, регулируется изменением угла установки лопастей рабочего колеса, при котором меняется характеристика насоса.
Регулирование задвижкой (дросселированием). Предположим, что пасос должен иметь подачу не Qa, соответствующую точке А пересе-чепия характеристики насоса с характеристикой пасосной установки, a Qb < Qa (рис. 2.33). Этой подаче соответствует рабочая точка В характеристика насоса. Чтобы характеристика насосной установки пересекалась с кривой напоров Н = / (Q) в точке В, необходимо увеличить потери напора в установке. Это осуществляется прикрытием регулирующей задвижкн, установленной на напорном трубопроводе. В результате увеличения потерь напора в установке характеристика пасосной установки пойдет круче и пересечет кривую напоров II — } (Q) насоса в точке В. При этом режиме потребный напор установки складывается из напора Яду, расходуемого в установке ври эксплуатации с полностью открытой задвижкой, и потери напора ha в задвижке. Таким образом, регулирование работы ыасоса дросселированием вызывает дополнительные потери энергии, снижающие КПД установки, поэтому этот способ неэкономичен. Однако благода ря исключительной простоте регу лированве дросселированием полу чило наибольшее распространение Регулирование изменением часто ты вращения насоса. Изменение час тоты вращения насоса ведет к изме нению его характеристики и, следо вательно, рабочего роясима (рис. 2.34). Для регулирования изменением частоты вращения необходимы двигатели с переменкой частотой вращения (электродвигатели постоянного тока, паровые и готовые турбины и двигатели внутреннего сгорания). Наиболее распространенные асинхронные электродвигатели с короткозамкнутым ротором практически пе допускают иаменения частоты вращения.
Применяется также изменение частоты вращения включением сопротивления в цепь ротора асинхронного двигателя с фазовым ротором, а также гидромуфтой, установленной между двигателем и насосом.
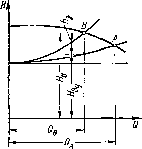
Регулирование работы пасоса изменением его частоты вращения более экономично, чем регулирование дросселированием. Даже применение гидромуфт и сопротивления в цепи ротора асинхроппого двигателя, связанное с дополнительными потерями мощности, экономичнее, чем регулирование дросселированием.
Регулирование перепуском. Оно осуществляется перепуском части жид-косин, подаваемой насосом, из напорного трубопровода во всасывающий по обводному трубопроводу, на котором установлена задвижка (ом. схему установки па рис. 2.36, задвижка 2). При изменении степени открытия этой задвижки изменяются расход перепускаемой жидкости и, следовательно, расход во внешней сети. Эноргйя жидкости, проходящей по обводному трубопроводу, теряется, поэтому регулирование ооропуском неэкономично.
Регулирование поворотом лопастей. Оцо применяется в средних и крупных поворотнолопастных осевых насосах. При повороте лопастей изменяется характеристика насоса и, следовательно, режим его работы (рис-. 2.35). КПД пасоса при повороте лопастей изменяется незначительно, поэтому этот способ регулиропания значительно экопомичнее регулирования дросселированием.
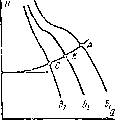
Рие. 2.35. Регулирование работы осевого пасоса изменением угла уетапошш лопастей
Рпе. 2.34. Регулирование работы насоса изменением частоты вращения
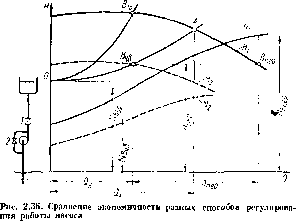
Сравпить экономичность регулирования работы насоса различными cnc’C'i-баии uponyj всего но потребляемой насосом мощности- Пусть кривая 0,1 (рис, 2.36) является характеристикой насосной установки при полностью от-крытой регулирующей задвшкке 1, а кривые Н1 и ,V, — кривыми паио;>л ч мощности характеристики пасоса прв частоте вращения ’h- Рея.им работы кл-соса определяется точкой А. Подача иасоса равна QМеньшую подачу QB можно получить следуюшдмо способами.
| Н -- | |
| У(а |
|
| _ Усв\ | |
| \ \ | |
|
хК\ | |
| Q |
1. Дросселированием. Прикрывая регулирующую задвижку 1, емешзсм рсжшшую точку uacoca вдоль еп> характеристики из Л в бдр. Мщцдссть, потребляемая насосом при работе на этом режиме, найдем но припой мощпости .V;. Она равна .VBnp.
2. Изменением частоты вращения. При уыеныиепии частоты вращения режимная точка смещается вдоль характеристика насоспои установив из А в Вч в. Этому режиму работы соответствует частота вращения пг. Мощность насоса определяется по кривом мощности Д"4, построенной для частоты вращения п2. Она равпа ^'Вцв.
3. Перепуском. Перепуск осуществляется открытием аадБижкп 2. Так как ери регулировании перепуском характеристика пасосной установки ее изменяется (задвижка 1 остается открытой полностью), то при расходе насоспои установки QB напор пасоса, равный потребному пааору установки, определяется ординатой //дар характеристики ОА насоспой установки. При этом наиоро режим пасоса соответствует точке 6пер. Жидкость, подаваемая насосом, частично уходит do впепппото сеть (QB), частично возвращается в подводящий трубопровод (qnep). Мощность насоса при работе на режиме Впср равна Nв аер.
Из рис. 2.3G следует, что наименьшая мощность получается ври ретулпро- • вании изменением частоты вращения, несколько больше мощность при регулировании дросселированием, самая большая — при регулировании перепуском:

NЕ < А'ддр < Л1 впер- Згот результат справедлив лишь для насосов, у которых с увеличением подачи мощность увеличивается (тихоходные в нормальные центробежные насосы). Еелп с увеличением иодачн мощность уменьшается (например, в осевых насосах), то регулирование перепуском акономичнее регулирования дросселированием.
2.17. Последовательная п параллельная работа насосов на сеть
Последовательоое соединение насосон обычно применяется для увеличения напора в тех случаях, когда один пасос ие может создать требуемого напора. При этом подача насосов одинакова, а общий напор равен сумме напоров обоих насосов, взятых при одпой и той же подаче. Следовательно, суммарная характеристика насосов I + II (рис. 2.37) получается сложением ординат кривых капоров I и II обоих насосов. Пересечение суммарной характеристики насосов с характеристикой пасоспой устаповки даст рабочую точку А, которая определяет подачу Q и суммарный напор Н\ + Иц обоих насосов. Проведя через точку А вертикальную прямую получим на пересечении ее с кривыми напоров I и II напоры насосов Нх и Нц.
При последовательном соединении насосов жадность, иодводп-мая к пасосу II, имеет значительное давление. При этой давление в насосе II может превысить велвчнну, допустимую по условиям прочности. В этом случае насос II следует размещать отдельно от насоса I, в такой точке напорного трубопровода, в которой давление жидкости снижается до безопасного для насоса II значения. Эту ючку можно определить, построив пьезометрическую линию напорного трубопровода.
Параллельное соединение насосов обычно применяют для увеличения подачи. Насосы, работающие параллельно на один длинный трубопровод, обычно устанавливают близко один от другого, в пределах одного машинного зала. На рис. 2.38 слева показана схема такой установки двух насосов. Так как насосы II и I находятся близко одни
от другого, а трубопровод, в* который оии работают, длинный, можно пренебречь сопротивлением подводящих и напорных трубопроводов до узловой точки О. Пусть приемные уровни обоих насосов одинаковы. При этом напор насосов одинаков, так как одинаково давление в точке О, создаваемое обоими насосами. Заменим оба насоса одним, имеющим подачу, равную сумме подач обоих насосов, взятых ?рв одинаковой напоре. Нро такой замене режим работы насосной установки не изменится. Для получения характеристики этого насоса или суммарной характеристики двух насосов, следует сложить абсциссы точек кривых напора // = / (Q) обоих насосов, взятых при
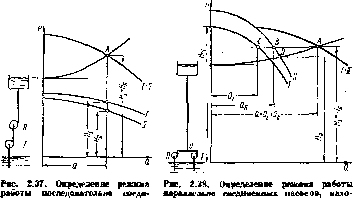
ненных насосов дшцпхея на близком расстоянии
одной и той же ординате. Ипымн словами, следует сложить кривые напоров I и II обоих насосов по горизонтали. Пересечете суммарной характеристики I II с характеристикой насосной установки даст рабочую точку А. Абсцисса точки А равпа суммарной подаче обоих насосов Q\ + ордината — напору насосов Hi — Нц. Проводя через точку А горизонтальную прямую, получим на пересечении с кривыми I и Ц напоров режимные точки С и В насосов I и II.
Определим режим работы двух разпых параллельно соединенных насосов, установленных на значительном расстоянии один от другого (рис. 2.39). При этом нельзя пренебречь сопротивлением подводящей и напорной линий до точкя В соединения трубопроводов. Пусть приемные уровни насосов находятся на разпых отметках. В точке В поставим пьезометр. Высота жидкости в нем равна пьезометрическому папору рв'(Рё) в сеченан В. Принимая за плоскость сравнения приемный уровень насоса I и пренебрегая скоростным налогом, получаем полный напор жидкости в сечении В:
y = zu+pBl(pg).
Для решения поставленной подачи изобразим зависимости полного напора ij в сечешш В от расхода жидкости по трубопроводам устаиовкп. Ось абсцисс графиков совместим с приемный уровнем насоса 1. Напишем уравнения движения жидкости по трубопроводам АВ, СВ л ВО.
Трубопровод АВ. Напор насоса I расходуется на подъем жидкости от уровня Л до уровня В на высоту zb, создание в точке В пьезометрического напора pn/'ipg) и преодоление гидравлических потерь
Лай в трубопроводе АВ (скоростным напором в сечении В пренебрегаем):
или, согласно нению (2.52),
y = H\ — hAB-
Hi -т pa!(pg) -b hAB
урав-
(2.53)
Для построения зависимости у от расхода жидкости в трубопроводе АВ следует, согласно уравнению (2.53), пз ординат характеристики [ насоса 1 вычесть гидравлические потери D трубопроводе АВ, пропорциональные расходу во второй степепи. В результате получим кривую 3В) которую назовем характеристикой насоса I, приведенной к точке В .
Трубопровод СВ. Напор насоса II расходуемся па подъем жидкости от уровня С до уровня В на высоту Zb — zc, создание в точке В пьезометрического штора рв/ipg) и преодоление гидравлических потерь hc-в в трубопроводе СВ :
JIn = (zu — zc) -V рв!(рё) + Лев, отсюда
y — JJ\\-\-ZQ—Лев • (2.54)
Для построения зависимости у от расхода по трубопроводу СВ необходимо к ординатам характеристики насоса II прибавить высоту Zc, или, другими словами, построить характеристику насоса II от его приемного уровня (уровень С) и от ординат получившегося графика П вычесть гидравлические потери в трубопроводе СВ. В результате получаем характеристику ИВ насоса II, приведенную к точке В.
Трубопровод BD. Уравнение Бернулли для сечений В и D имеет вид (скоростиьш напором в сечении В пренебрегаем):
гь -Ь PDf(pg) = 2d + Лвс.
Отсюда у —Zd + ^BD-
Для построения кривой BD зависимости у от расхода г. трубопроводе BD необходимо и постоянной величине г-о прибавить гид;»:; и-личсские потери в трубопроводе BD, пропорциональные расходу во второй степеип.
Расход в трубопроводе BD равеп сумме расходов в трубопроводах АВ и СВ:
Qbd-Q\-\-Qii-
(2.50)
Построим кривую 1В Ч- 11В зависимости у от суммарною расхода в трубопроводах АВ и СВ. Для этого необходимо для каждого значения у суммировать абсциссы приведенных характеристик \В я 11В (суммировать кривые [# и [I# по горизонтали). Насоспая установка работает при таком значении у, при котором расход, в трубопроводе BD равен сумме расходов в трубопроводах АВ и СВ, т. е. при котором абсциссы суммарной характеристики I# Н- 315 и кривой BD одинаковы. Этому удовлетворяет точка М пересечения этих кривых. Абсцисса точки М равна расходу в трубопроводе BD. Ордината раина у. Зная величину у, можно иантга по приведенным характеристикам 3# и ПЯ расходы Qf и Qu жидкости в трубопроводах АВ н СВ, равные подачам насосов I и II, а по известным подачам Qi п Qu по характеристикам I и П насосов найти их папоры Нх и Нц.
2.18. Работа пасоса еа разветвленный трубопровод
На рис. 2.40 изображена схема установки с разветвленной сетью. Насос подлет жидкость в два резервуара С и D, расположенные на разпых уровнях. Требуется определить режим работы пасоса и расходы в обоих ответвлениях.
Возможны два случая работы пасоса па сеть. *
1. Уровень жидкости в пьезометре, установленном в точко В, выше уровня жидкости в резервуаре D (у > Zp). В этом случае жидкость от точки В движется как в резервуар С, так и в резервуар D.
2. Уровень ишдкосш в пьезометре ниже уровня жидкости в резервуаре I) (у < ги). В этом случае жидкость по трубопроводу BD движется в направлении от точки D к точко В.
Разберем сначала первый случай работы пасоса па сеть. Напишем уравпепия движения жидкости по трубопроводам АВ, ВС и BD.
Трубопровод АВ. Напор насоса, установленного па трубопроводе, тратится на подч,еи жидкости па высоту zB, создание в точке В пьезометрического напора рв!(№) к на преодоление гидранличссиих потерь }гЛц в трубопроводе АВ (скоростным напором в сечении В пренебрегаем):
Построим график зависимости между напорол у в узловой точке В и расходом в трубопроводе АВ, Для этого, согласно уравнению (2.57), необходимо из ординат характеристики Н = j (Q) насоса вычесть гидравлические потери в трубопроводе АВ. В результате получим штриховую линию В — характеристику насоса, приведенную к точке В.
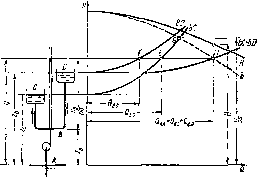
Рис. 2.40. Определение режима работы насоса на разветвленную есть (первый случай)
Трубопровод ВС. Из уравнения Бернулли, написавпого для сечений В в С, получим
ZB-fPB/(pg)=2j-ffcflC ЕЛИ y^Zc-rltDC-
(2.г>8)
Прибавив к постоянной величине zc гидравлические потери hBC в трубопроводе ВС, пропорциональные расходу во второй степени, получим график ВС зависимости между у и расходом в трубопроводе ВС.
Трубопровод BD. Уравнение движения жидкости по трубопроводу BD такое же, как и для трубопровода ВС:
y=*zD + liBD- (2.59)
Прибавив к постоянной zD ординаты кривой зависимости гидравлических потерь hnn в трубопроводе BD от расхода, полупим кривую BD, представляющую собой зависимость между у и расходом в трубопроводе ВТ).
Расход в трубопроводе АВ равен сумме расходов в трубопроводах ВС и BD-.
Qab = Qbc 'г Qdd.
(2.60)
Построим кривую ВС 4- BD зависимости у от суммы расходов в трубопроводах ВС и BD. Для этого необходимо суммировать кривые ВС и BD по горизонтали. Насосная установка работает при таком значении у, при котором расход в трубопроводе АВ равен сумме расходов в трубопроводах ВС и BD, т. е. при котором абсциссы суммарной кривой ВС 4- BD и приведенной характеристики насоса В одинаковы. Этому удовлетворяет точка М пересечения этих кривых.
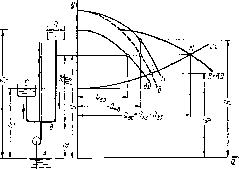
Рис. 2.41. Определение режима работы насоса на разветвленную сеть (второй случай)
Абсцисса точки М равна расходу в трубопроводе АВ и, следовательно, подаче насоса. Ордината равна у. Зная подачу насоса, по его характеристике Н = / (Q) определяем напор Н. Зная напор у в точке В, можно найти расходы в трубопроводах ВС и BD. Для этого следует через точку М провести горизоптальпую линию до пересечения с кривыми ВС и BD. Абсциссы точек пересечения Е и ? дадут искомые расходы в ответвлевиях ВС и ВТ).
Перейдем ко второму случаю работы насоса на сеть, при котором уровень жидкости в пьезометре ниже уровня жидкости в резервуаре D (рис. 2.41).
Методика решения этой задачи одинакова с методикой решения предыдущей задачи. Уравнения движения жидкости по трубопроводам АВ и ВС во втором случае пе отличаются от уравнений в нервом случае. Следовательно, кривые В а ВС зависимости напора у в точке В от расходов в трубопроводах АВ и ВС во втором случае строятся так же, как и в первом.
Рассмотрим движение жидкости по трубопроводу BD. Уравнение Бернулли для сечений D и В имеет вид:
Яо = *я + рв/р?-Мпо или y = zn~!iBD. (2.(51)
Следовательно, для построения кривой BD зависимости у от расхода в трубопроводе BD необходимо от постоянной zD вычесть ординаты кривой зависимости гидравлических потерь в трубопроводе BD о-r расхода.
Расход 1з трубопроводе ВС равен сумме расходов в трубопроводах АВ и BD-,
Qbc-Q.<b + Qbd. (2.62)
Построим кривую В -\- BD зависимости у от суммы расходов в трубопроводах АВ и BD. Для этого сложим кривые В и BD по горизонтали. Установка работает при таком значении у, при котором сумма расходов в трубопроводах А В и BD (абсцисса точки кривой В -\-BD) равна расходу в трубопроводе ВС. Этому условию соответствует точка М пересечения кривых ВС и В 4- ВО. Абсцисса этой точки равна расходу в трубопроводе ВС, ордината — у. Но известному значению у определяем по кривым В и BD расходы Qad 0 Qbd в трубопроводах АВ и BD. По известной подаче насоса (расход <?ав) находим его напор II по характеристике II = f (Q).
Из приведенного следует, что для определения режима работы насоса иа разветвленную сеть необходимо предварительно узпать направленно движения жидкости по трубопроводу BD. Методика анализа следующая. Стропм зависимости В и ВС напора у в узловой точке В от расходов в трубопроводах АВ и ВС, как указано выше. Предположим, что трубопровод BD перекрыт. В этом случае расходы в трубопроводах АВ и ВС одинаковы. Этому удовлетворяет точка G пересечения кривых В и ВС. Ордината точки G определяет положение уровня жидкости в пьезометре при перекрытом трубопроводе BD. Если точка выше уровня жидкости в резервуаре D (гдз > zD, рис. 2.40), то при открытии трубопровода BD жидкость потечет от точки В в резервуар D — первый случай работы. Если же г/о < гц (см. рис. 2.41), то при открытии трубопровода BD жидкость потечет из резервуара D к точке В — второй случай работы.
