Теоретические исследования фильтрации в пласте с трещинами гидравлического разрыва
ТЕОРЕТИЧЕСКИЕ ИССЛЕДОВАНИЯ ФИЛЬТРАЦИИ В ПЛАСТЕ С ТРЕЩИНАМИ ГИДРАВЛИЧЕСКОГО РАЗРЫВА
2.1. ИССЛЕДОВАНИЯ СТАЦИОНАРНОГО ПРИТОКА К ТРЕЩИНЕ ГИДРОРАЗРЫВА
В случае линейной фильтрации несжимаемой жидкости распределение давления p в пласте и в трещине стационарное и определяется уравнением Лапласа [7, 9, 92]:
Api = 0, i = r, f. (2.1)
Здесь индекс i = r соответствует пласту, индекс i = f - трещине. Обычно предполагается, что пласт имеет постоянную толщину h и проницаемость kr; скважина, расположенная в начале координат, пересекается симметричной вертикальной трещиной, параллельной оси Ох; включение, моделирующее трещину гидроразрыва, характеризуется проницаемостью kf (рис. 2.1). Трещина считается недеформируемой.
На линии раздела областей давление и нормальная составляющая скорости должны быть непрерывны [81,85]:
Pr = Pf kr = kf ¦ (2.2)
on on
Здесь n - направление нормали к границе трещины.
Впервые приток к скважине, пересеченной естественной вертикальной прямолинейной трещиной неограниченной длины, в условиях стационарной фильтрации ис-
Пласт
41
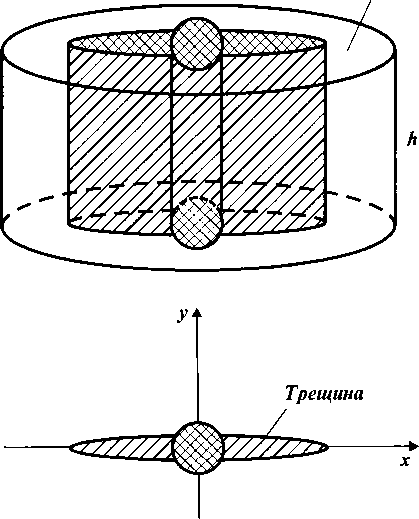
Рис. 2.1. Две области фильтрации: пласт и вертикальная трещина
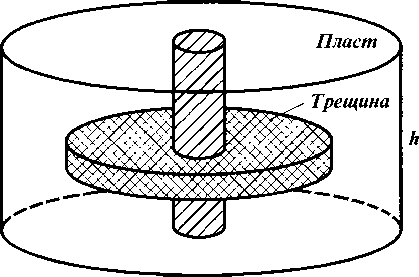
Рис. 2.2. Скважина с горизонтальной дисковидной трещиной гидроразрыва
следовался М. Маскетом [71]. В зависимости от соотношения проницаемостей пласта и трещины и ширины трещины получено распределение притока из пласта в трещину и давления вдоль нее.
Необходимость оценки эффективности гидравлического разрыва пласта вызвала появление работ по созданию методов расчета производительности скважин, пересеченных трещинами гидроразрыва [5, 57, 61, 66, 68, 73, 80, 86, 93, 95, 98-100, 103, 157, 177, 205, 206]. Наряду с вертикальными рассматривались горизонтальные осесимметричные дисковидные трещины (рис. 2.2) [5, 57, 61, 95, 98, 99, 103, 157, 205].
Для того, чтобы получить аналитическое выражение для расчета притока однородной жидкости к скважине с горизонтальной трещиной от удаленного контура питания радиусом Rc, принимались различные допущения. Предполагалось, что трещины являются бесконечно проводящими (идеальными), т.е. kf ^ да, поэтому давление на контуре трещины постоянно и равно забойному [5, 95]. Истинное распределение линий тока вне трещины заменялось на несколько искаженное [5, 95]. М.И. Швидлером [95] получена приближенная формула притока к идеальной горизонтальной трещине радиусом 1, расположенной в центре пласта, при условии, что 0,05 < 1/R < 0,1, 0,02 < h/R < 0,1:
R '
Здесь |j. - вязкость жидкости, pc и pw - давление на удаленном контуре пласта и на забое скважины соответственно. В работе А. Бана, А.Ф. Богомоловой, В.А. Максимова, В.Н. Николаевского, В.Г. Оганджанянца, В.М. Рыжика [5] предложена приближенная формула для эффективного радиуса скважины с горизонтальной дисковидной трещиной, расположенной в центре пласта постоянной толщины, определенного как радиус эквивалентной совершенной скважины: re « 1exp[-0,221(1/h - 0,11)-1]. Стационарный приток к горизонтальной трещине гидроразрыва исследовался также в работах [157, 205]. J.H. Hartsock, J.E. Warren [157] задача решалась в конечно-разностной форме, учитывалось влияние анизотропии пласта по проницаемости, смещение трещины вдоль вертикали относительно центра пласта, оценивалась эффективность создания нескольких дисковидных трещин.
В [61, 80, 98-100, 103] рассматривались трещины конечной проводимости, т.е. заполненные проппантом. В предположении, что течение в горизонтальной трещине радиальное, а в вертикальной - плоскопараллельное, Ю.М. Шехтманом [98-100] получены распределения давления в пласте, в центре которого расположена горизонтальная или вертикальная трещина гидроразрыва. Принятая гипотеза о характере течения в трещине позволила сформулировать граничные условия для внешней задачи, описывающей фильтрацию в пласте, и решать ее независимо от расчета течения в трещине. Представленные результаты показали, что введение в трещину заполнителя приводит к снижению дебита до 25 %. В работе Н.С. Пискунова [80] для описания притока к горизонтальной трещине была сформулирована и решалась задача сопряжения (2.2). Исследовалось распределение давления в двух смежных областях: в пласте и в трещине. Показано, что эффект гидравлического разрыва существенным образом зависит от проницаемости песка, заполняющего трещину. Эффект от гидроразрыва более значителен в пластах малой мощности. В.И. Щуров, А.Ф. Трубина [103] для анализа притока к центральной скважине с горизонтальной трещиной посередине в круговом однородном пласте использовали электролитическое моделирование. Данные электромоделирования показали, что в результате гидроразрыва можно ожидать увеличения дебита в 2-3 раза, эффект от гидроразрыва возрастает с увеличением радиуса трещины, однако при больших значениях радиуса его увеличение мало сказывается на приросте дебита. Фактически встречающееся в промысловой практике повышение дебита в 5 раз и более связано с уменьшением проницаемости в призабойной зоне скважины.
В работе W.J. McGuire, V.J. Sikora [177] с использованием электроаналогового компьютера исследована производительность скважин с вертикальными трещинами гидроразрыва в ограниченном пласте с непроницаемыми границами. Определялся коэффициент продуктивности скважины в
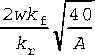
зависимости от относительной проводимости трещины
и ее полудлины 1. Здесь w - половина раскрытия трещины, А -площадь зоны дренирования скважины.
Задача о притоке к вертикальной трещине эллиптической формы конечной проводимости в однородном пласте с удаленным
контуром питания
рассмотрена M. Prats [206], В.В. Кадетом, В.И.
Селяковым [37]. Получено аналитическое
решение задачи для пласта и для трещины с
учетом условий сопряжения (2.2), исследовано
распределение давления в пласте вокруг
трещины в зависимости от ее полудлины и
параметра a = nkr . Введен
эффек-
2kfw
тивный радиус скважины, пересеченной трещиной гидроразрыва, ге как радиус эквивалентной цилиндрической скважины, который может использоваться для расчета коэффициента продуктивности. В случае трещины бесконечной проводимости a = 0 и re = 1/2. Показано существование предельной длины трещины, превышение которой не приводит к увеличению коэффициента продуктивности скважин [37]. В работе [5] вычислен эффективный радиус скважины с n идеальными, звездообразно отходящими вертикальными трещинами гидроразрыва re = = 21/22/n.
В работе А.Ф. Зазовского, Г.Т. Тодуа [35] исследована задача о притоке к вертикальной трещине конечной проводимости, длина которой намного больше толщины пласта, при различном раскрытии трещины: постоянном, параболическом выпуклом, линейном и параболическом вогнутом. Показано, что создавать очень длинные трещины не всегда целесообразно, так как фильтрационный поток в трещину при ее большом гидравлическом сопротивлении локализуется вблизи скважины, а удаленная часть трещины не оказывает влияния на значение коэффициента продуктивности. В зависимости от формы раскрытия трещины рассчитаны отношения коэффициентов продуктивности скважины после и до гидроразрыва для трещин предельной длины. Выявлено существенное влияние формы раскрытия на коэффициент продуктивности.
В связи с задачей извлечения глубинного тепла Земли из сухих горных пород А.Ф. Зазовским, А.В. Лемехой, Р.П. Федоренко [33, 34] рассматривается задача о циркуляции жидкости в плоской трещине гидроразрыва, сообщающейся при помощи двух скважин (добывающей и нагнетательной) с теплообменником, находящимся на поверхности земли. Исследуются нелинейные эффекты, связанные с зависимостью гидравлической проводимости циркуляционной системы от раскрытия трещины и, следовательно, от давления нагнетания и отбора жидкости. Выявлена возможность частичного или даже полного смыкания поверхностей трещины в окрестности отбирающей скважины в зависимости от режима течения жидкости.
Некоторые задачи о возмущении плоского фильтрационного потока трещинами различного происхождения рассматривались также в [1, 20, 90, 91]. Основным математическим аппаратом в этих работах является метод комплексного потенциала [12, 13, 24-26, 56, 78, 79].
2.2. ИССЛЕДОВАНИЯ НЕСТАЦИОНАРНОГО ПРИТОКА К ТРЕЩИНЕ ГИДРОРАЗРЫВА
Интерпретация поведения давления на разных стадиях притока сжимаемой жидкости в скважину после проведения гидроразрыва осуществляется на основе решений задач нестационарной фильтрации [9, 75]. В этом случае фильтрация жидкости в пласте и в трещине описывается уравнением упругого режима [7, 102]
*Pi = ^, i= Г, f (2.3)
k1 dt
где ф; и ci - пористость и эффективная сжимаемость пласта и трещины соответственно. В упрощенной постановке трещина предполагается идеальной и учитывается как линейный сток (источник), на котором задано постоянное давление или отбор жидкости [113, 131, 136, 149-152, 182, 196, 197, 207, 208, 211, 216, 234].
В работе A.C. Gringarten, H.J. Ramey Jr. [149] развит аппарат функций Грина применительно к задачам неустановившейся фильтрации. Получены функции мгновенного источника в ограниченных и неограниченных пластах для точечного и распределенных источников различной геометрии. A.C. Gringarten, H.J. Ramey Jr., R. Raghavan [150-152] применяют эти результаты для определения поля давления вокруг вертикальной и горизонтальной трещин. Рассматриваются как трещины бесконечной проводимости, так и с равномерным распределением потока через границы трещины. Выделены периоды фильтрации, различающиеся по характеру зависимости забойного давления от времени. Для горизонтальной трещины характерны четыре периода: первый, обычно очень непродолжительный, - радиальная фильтрация в трещине, второй - вертикальная линейная фильтрация от кровли и подошвы пласта к трещине, третий - переходный и четвертый -радиальная фильтрация в пласте к трещине. В [150] вычислен радиус влияния ri - расстояние от оси скважины, начиная с которого функция псевдоскин-фактора, обусловливающая отличие фильтрации в пласте от радиальной, пренебрежимо мала. Показано, что скин-эффект не зависит от времени и пренебрежим на расстояни-
коэффициент анизотро-
ях более
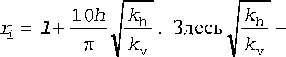
пии пласта. Согласно данным [151, 152], для вертикальной трещины в квадратном пласте с непроницаемыми границами характерны три основных периода фильтрации: линейное течение в трещине, псевдорадиальное течение в пласте и псевдостационар-ное течение от границ пласта к трещине. В случае неограниченного пласта выделяются периоды линейной и псевдорадиальной фильтрации, а также переходный период между ними. График зависимости забойного давления от времени в безразмерных переменных, соответствующий периодам линейной и псевдостацио-нарной фильтрации, характеризуется различными наклонами прямой в логарифмических координатах. Для периода линейной фильтрации p ~ Vt, при псевдостационарной фильтрации p ~ t. Среднему периоду псевдорадиального течения соответствует график прямой в полулогарифмических координатах. В случае вертикальных трещин, вскрывающих неограниченный пласт не на всю толщину, доля вскрытой толщины влияет лишь на характеристику начального периода линейной фильтрации и не существенна для периода псевдорадиального течения [211].
В работах E. Ozkan, R. Raghavan [196, 197] решения задач не-установившейся фильтрации, обусловленной точечным или линейным источником (вертикальная трещина, горизонтальная скважина), в неограниченном, прямоугольном или круговом пласте получены методом преобразования Лапласа. Разработаны методы исследования скважин, основанные на анализе изображений наблюдаемых зависимостей.
В работах H. Cinco-Ley [125], H. Cinco-Ley, V.F. Samaniego [126], H. Cinco-Ley, V.F. Samaniego, N. Dominguez [128] рассматриваются симметричные вертикальные трещины конечной проводимости, вскрывающие однородный пласт на всю толщину. Трещины предполагаются прямоугольными с непроницаемыми тор-
цами. Приток осуществляется только через боковые поверхности трещины. Течение в трещине предполагается одномерным:
fyfUCf dpf kf dt
(2.4)
dx
d2pf + ц q(x,t)
kf 2wh
с начальными и граничными условиями
I _ I k dpt
pfI y_±w _ pr y_±w , kf _
dy
dpr
dy
y_ ±w _ 0.
(2.5)
x ±l
x 0
dpf
pf t 0 p0, f
dx
y_ ±w
qw ц dp
4whkf dx
k
Здесь
2krh dpr
(2.6)
qX,t) _ -
Ц dy
y_0
поток из пласта в трещину.
Для решения задачи (2.3)-(2.6) в [128] применяется полуанали-тический метод, который состоит в следующем: трещина разбивается на 2N одинаковых сегментов, и предполагается, что в течение одного временного шага поток в каждый сегмент постоянный. Это позволяет применить известные методы [149] для получения аналитических решений для каждого сегмента трещины. Результирующие распределения давления в пласте и в трещине находят путем суммирования полученных соотношений по сегментам и по времени. Неизвестные потоки для каждого сегмента определяют исходя из граничных условий (2.5), путем решения системы алгебраических уравнений методом Ньютона.
Выделяют четыре стадии течения жидкости в неограниченном пласте в окрестности вертикальной трещины (рис. 2.3). Основным является линейное течение вдоль трещины из ее удаленных частей к скважине. Затем это течение дополняется плоскопараллельным потоком из пласта в трещину через ее поверхности (так называемый билинейный период). Этот период характеризуется зависимостью p ~ tft. Постепенно линейное течение из пласта в трещину становится основным, и потоком от краев трещины можно пренебречь. На заключительной стадии приток жидкости идет из удаленных от скважины областей - это так называемый псевдора-диальный период. Для определения проводимости трещины и ее длины наиболее важна информация о первых двух периодах фильтрации. Исходное представление о направлении потоков в пласте и в трещине в билинейном периоде позволяет упростить уравнения (2.3)-(2.6) и исследовать задачу аналитически методом преобразования Лапласа. Показано, что в безразмерных переменных динамика давления в билинейном периоде практически зависит только от одного параметра - безразмерной проводимости трещины 2kfwlkrl [128]. В частности, этой величиной определяется начало периода линейной фильтрации, когда p ~ Int. Для определения параметров пласта, таких как проницаемость, пьезопроводность, обычно используются данные о поведении давления на более поздней стадии - в псевдорадиальном периоде или независимые измерения, например, до проведения гидроразрыва.
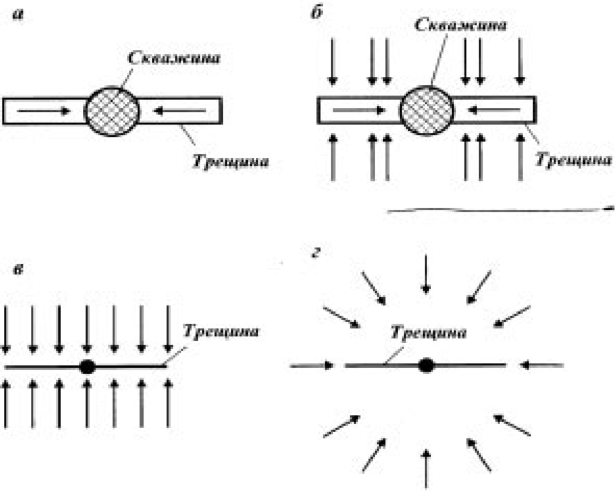
Рис. 2.3. Четыре стадии неустановившегося течения жидкости в окрестности вертикальной трещины гидроразрыва.
Фильтрация: а - линейная в трещине, 6 - билинейная, в - линейная в пласте, г -псевдорадиальная
В пластах с низкой и сверхнизкой проницаемостью продолжительность периодов неустановившейся фильтрации значительно выше, чем в более проницаемых пластах. Поэтому методы определения коэффициента продуктивности скважин по индикаторным кривым при стационарном режиме отбора жидкости могут использоваться лишь для высоко- и среднепроницаемых пластов. Внедрение гидроразрыва пластов с низкой и сверхнизкой проницаемостью сделало необходимым введение и использование методов расчета коэффициентов продуктивности по данным неустано-вившегося притока. В работе [181] предложена методика определения коэффициентов продуктивности для скважины с вертикальной трещиной гидроразрыва, расположенной в центре замкнутого прямоугольного элемента пласта. При фиксированных соотношениях длин сторон элемента пласта построены графики расчетных зависимостей безразмерного перепада давления на скважине от времени для заданных значений безразмерной проводимости трещины и отношения полудлины трещины к длине расчетного элемента. Коэффициент продуктивности определяют для нужного момента времени, исходя из рассчитанного безразмерного перепада давления. В [181] рассматривается однофазная фильтрация нефти, поэтому получаемые коэффициенты продуктивности могут использоваться только при давлениях выше давления насыщения. Для оценки дебита скважин при забойном давлении ниже давления насыщения, когда имеет место двухфазная фильтрация нефти и газа, используются специальные корреляционные зависимости [241]. В работе M.J. Economides, K.G. Nolte [137] представлена пошаговая процедура построения коэффициентов продуктивности при неустановившейся фильтрации нефти и газа к скважине с трещиной гидроразрыва с учетом зависимостей [241].
Методике использования кривых восстановления давления для идентификации параметров пласта и трещины посвящены работы [120, 122, 137, 138, 145, 151, 161, 163, 210, 214]. Фактические данные об изменении давления и дебита в графическом виде (обычно в логарифмических координатах) сопоставляются с результатами расчетов. В [118] эта задача решается с учетом зависимости проницаемости пласта и проводимости трещины от давления.
D. Malekzadeh, F.U. Khan, J.J. Day [172] для определения параметров пласта и трещины предлагают использовать решение задачи о вертикальной, бесконечно проводящей трещине в замкнутом пласте [152] и в качестве определяющего параметра выбрать не проводимость трещины, как в [126, 128], а ее эффективную длину, учитывая при этом скин-эффект, загрязнение пласта вокруг трещины и т.д. D. Tiab [234] на основе этого же аналитического решения предложил новую методику определения скин-фактора, проницаемости пласта и полудлины трещины без подгонки графических зависимостей давления от времени по промысловым данным. Для расчетов им используются некоторые характерные точки на экспериментальных графиках зависимостей безразмерного давления p и произведения —— t от безразмерного времени t
dt
в логарифмических координатах.
В некоторых случаях не удается решить задачу идентификации параметров пласта и трещины в рамках модели однородного пласта, так как вид реальных зависимостей давления от времени оказывается отличным от теоретического. Один из способов решения задачи предложен R.A. Beier [113], им получены соответствующие зависимости для различных периодов фильтрации в рамках модели пласта, имеющего фрактальную структуру. Пористость и проницаемость фрактальной сети определяются выражениями:
ф(г)= k(r) = к0(Г L0ydtQ / ds-1).
Здесь г - расстояние от забоя скважины, L0 - масштаб длины, ds и df - параметры сети. В частности, для однородного двумерного пласта ds = df = 2. Для пласта, имеющего фрактальную структуру, давление на контуре бесконечно проводящей трещины изменяется в зависимости от времени по степенному закону: для периода линейной фильтрации p ~ ^~(*/2)(1-Шб, при псевдорадиальной фильтрации p ~ t^ds/2.
Аналитические зависимости, используемые для идентификации параметров пласта и трещины, получены с учетом различных упрощающих предположений, поэтому R.G. Agarwal, R.D. Carter, C.B. Pollock [106, 107], W.J. Lee, S.A. Holditch [170] предлагают решать эту задачу путем численного моделирования. Рассматривается двумерная однофазная фильтрация реального газа. В результате конечно-разностной аппроксимации задача определения поля давлений на каждом временном слое сводится к системе линейных уравнений, которая решается прямым или итерационным методом. Трещина моделируется ячейками небольшой ширины высокой проницаемости и пористости. В окрестности скважины, концов трещины, а также вдоль трещины в направлении, нормальном к ее оси, используются мелкие расчетные ячейки. Сопоставляя промысловые данные о поведении давления с графиками [107] либо с численным решением задачи о притоке жидкости из скважины с трещиной при работе скважины на излив и при воспроизведении истории [170], определяют длину и проводимость трещины, а также проницаемость коллектора. Учитывая, что промысловые данные обычно допускают неединственную интерпретацию, предпочтительно использовать данные о проницаемости пласта, определенные другим независимым методом. Проведенный в [170] анализ промысловой информации показал, что в большинстве случаев рассчитанная после гидроразрыва длина трещин составляет лишь 70 % от запроектированной длины, что объясняется несовершенством теоретических моделей и технологических операций.
Определение проницаемости пласта по данным минигидроразрыва позволяет значительно сократить продолжительность исследования скважины. Мини-гидроразрыв часто проводят перед проведением гидроразрыва с целью уточнения технологии. При этом жидкость разрыва закачивают с постоянным расходом до достижения давления разрыва; через 20-30 мин закачка прекращается, забойное давление снижается, а трещина смыкается. Специальная математическая модель, учитывающая распространение трещины и материальный баланс жидкости, позволяет оценить утечки жидкости разрыва в пласт и по поведению давления определить проницаемость пласта и сопротивление поверхности трещины [175].
Автомодельные решения задачи о вытеснении пластовой жидкости более вязкой жидкостью разрыва при глубокопроникающем гидравлическом разрыве пласта получены Ю.Н. Гордеевым [15], Ю.Н. Гордеевым, А.Ф. Зазовским [17, 148], Ю.Н. Гордеевым, В.М. Ентовым [16]. Исследовано распределение давления в окрестности растущей трещины, оценены утечки жидкости разрыва в пласт. В рамках модели Т.К. Perkins, L.R. Kern [204] показано, что при создании вертикальных трещин, когда основной вклад в перераспределение потока жидкости в трещине вносят фильтрационные утечки, а не изменение ее объема под действием градиента давления, технологически и экономически выгоднее использовать жидкости разрыва небольшой вязкости. Это связано с тем, что с увеличением вязкости жидкости разрыва уменьшается скорость ее течения в трещине, а следовательно, и скорость распространения трещины. Поэтому возрастают время, необходимое для создания трещины заданной длины, и потери жидкости вследствие ее утечек в пласт. Высоковязкие жидкости следует использовать лишь на стадии закрепления трещин.
Для описания процесса вытеснения пластовой жидкости жидкостью разрыва в окрестности трещины J.S. Torok, S.H. Advani [237] получено аналитическое решение одномерной задачи о продвижении границы раздела ньютоновской пластовой жидкости и неньютоновской жидкости псевдопластического типа, закон движения которой имеет вид: vn = —к Vp. Здесь v - скорость
^ eff
фильтрации, |j.eff - эффективная вязкость. В простейшем случае при некоторых рациональных значениях показателя степени n движение границы раздела описывается степенной зависимостью от времени. Аналогичная задача в более общей постановке исследовалась Yi Tongchun, J.M. Peden [236]: ими рассмотрено поршневое вытеснение пластовой жидкости жидкостью разрыва, подчиняющейся степенному закону, с учетом трех различных зон фильтрации: фильтрационной корки вокруг трещины, зоны проникновения фильтрата в пласт и зоны, занятой пластовой жидкостью. Учитываются динамика образования фильтрационной корки и условия сопряжения на границах зон. Задача решается численно конечно-разностным методом.
Высокая скорость фильтрации в трещинах гидроразрыва приводит к проявлению нелинейных эффектов и вызывает отклонение закона фильтрации от закона Дарси [246]. Эффект нелинейности оценивается в [133], где используется двучленный закон фильтрации в следующем виде [7, 9]: dpf
= ^ + ppv2. (2.7)
дх
kf
Здесь v - скорость фильтрации, p - плотность жидкости. Параметр р для трещин гидроразрыва определяется корреляционной зависимостью р = b/kf ([kf] = мкм2, [р] = МПа-с2/кг), в которой
эмпирические коэффициенты а и b зависят от размеров зерен проппанта [133] (см. табл. 2.1).
Анализ уравнений фильтрации к скважине с трещиной гидроразрыва с учетом нелинейного закона (2.7) проводился на базе конечно-разностного подхода S.A. Holditch, R.A. Morse [162] и так называемым “полуаналитическим” методом K.H. Guppy, H. Cinco-Ley, H.J. Ramey, V.F. Samaniego [154], основы которого описаны в работе [126]. Показано, что нелинейный член надо учитывать, если скорость фильтрации превышает некоторое пороговое значение. Неучет нелинейного эффекта приводит к существенному занижению проводимости трещины, определяемой по данным неус-тановившейся фильтрации [155]. Предложена методика определения истинных значений проводимости трещины с учетом кажущихся (заниженных) ее значений и расхода жидкости.
В настоящее время гидроразрыв применяется для интенсификации скважин не только в низкопроницаемых, но и в средне- и высокопроницаемых пластах. В этом случае безразмерная проводимость трещины 2kfw/kr1 мала, и эквивалентный радиус скважины, обычно используемый в приближенных расчетах, определяется не полудлиной трещины, а ее проводимостью [226]:
re = 0,28(2kfw/kr). (2.8)
Таблица 2.1
| Размер зерен, меш |
a | b |
| 8-12 | 1,24 | 332 |
| 10-20 | 1,34 |
263 |
| 20-40 |
1,54 | 265 |
|
40-60 | 1,60 | 110 |
Эта зависимость справедлива при 2kfw/krl < 1. Заметим, что при неограниченном возрастании величины 2kfw/krl эффективный радиус стремится к 1/2. Зависимость (2.8) может служить обоснованием технологии TSO (tip-screen-out), позволяющей создавать достаточно широкие короткие трещины в средне- и высокопроницаемых пластах.
В результате импульсного гидроразрыва образуется несколько трещин, радиально расходящихся от забоя скважины. Исследование нестационарного притока к скважине с двумя ортогональными симметричными трещинами в однородном пласте на основе двумерной однофазной конечно-разностной модели проведено H. Al-Hashim, M. Kissami, H.Y. Al-Yousef [109]. Для таких систем в случае конечной проводимости трещин не наблюдаются периоды билинейного и линейного течения из пласта. Для бесконечно проводящих трещин период линейной фильтрации имеется при любых соотношениях полудлин трещин yf/xf. Полудлина трещины, рассчитываемая по результатам исследования линейного периода фильтрации, равна сумме полудлин в двух ортогональных направлениях: 1 = xf + yf, независимо от отношения yf/xf. Период псевдо-радиальной фильтрации начинается тем раньше, чем меньше различаются полудлины трещин и чем ниже их проводимость. Показано, что при высоких значениях безразмерной проводимости 2kfw/kr(xf + yf) одна трещина с полудлиной l = = xf + yf позволяет получить более высокий дебит, чем две ортогональные трещины с полудлинами xf и yf. С другой стороны, при низкой безразмерной проводимости две ортогональные трещины оказываются предпочтительнее, чем одна трещина суммарной длины.
2.3. ОСОБЕННОСТИ ПРИТОКА К ТРЕЩИНАМ ГИДРОРАЗРЫВА ПЕРЕМЕННОЙ ПРОВОДИМОСТИ
Асимметричные трещины и трещины переменной проводимости рассматриваются C.O. Bennett, A.C. Reynolds, R. Raghavan, J.E. Elbel [116], C.O. Bennett, N.D. Rosato, A.C. Reynolds, R. Raghavan [117], H. Cinco-Ley, V.F. Samaniego [127], M. Soliman [227, 228] путем численного моделирования. При исследовании скважины на неустановившемся режиме фильтрации в начальный период времени давление определяется проводимостью ближайшей к забою части трещины. Если проводимость монотонно убывает от скважины к концу трещины и изменяется не более чем в 20 раз, то на поздней стадии трещина ведет себя как постоянно проводящая с проводимостью, равной среднему арифметическому. В общем случае на поздней стадии динамика давления зависит от распределения проводимости вдоль трещины, причем это распределение не может быть выявлено по данным исследования скважины, так как трещина ведет себя как однородная с эквивалентной проводимостью, отличной от среднего значения. Если внутри трещины имеется низкопроницаемое включение (“пробка”), то эффективная длина трещины снижается. Если это включение находится вблизи скважины, скин-эффект может привести к значительному снижению ее эффективного радиуса [127, 215]. Обратное не всегда имеет место: заканчивание трещин высокопрочным крупнозернистым проппантом (т.е. создание в призабойной зоне трещины высокопроницаемого включения) не всегда позволяет получить значительный прирост производительности скважины. При проектировании гидроразрыва наиболее выгодно стремиться к осуществлению в трещине режима постоянного градиента давления, а не к созданию трещин постоянной проводимости.
Для асимметричных трещин различие длин крыльев существенно влияет на поведение давления в окрестности трещины, если
безразмерная проводимость удовлетворяет условию 0,1 < 2kfw/kr1 < 100, а отношение длины меньшего крыла трещины к длине большего менее чем 0,3.
2.4. ИССЛЕДОВАНИЯ ПРИТОКА К ТРЕЩИНАМ ГИДРОРАЗРЫВА В НЕОДНОРОДНЫХ ПЛАСТАХ
Анализ фильтрации к скважине, пересеченной трещиной гидроразрыва и находящейся во включении, проницаемость которого отлична от проницаемости основного пласта, проведен C.-C. Chen, R. Raghavan [123], W. Chu, G.D. Shank [124], H. Cinco-Ley, V.F. Samaniego [127]. В работах [123, 124] рассматривается круговое включение, в центре которого находится скважина; при этом вертикальная трещина либо выходит за пределы этого включения, либо целиком содержится внутри него. Включение небольших размеров может моделировать загрязненную призабойную зону. Если полудлина трещины хотя бы в 2 раза превышает радиус включения, то скин-эффект, обусловленный загрязнением призабойной зоны, становится несущественным и не влияет на коэффициент продуктивности скважины после гидроразрыва.
Область пониженной проницаемости вытянутой формы, окружающая трещину, может возникнуть вследствие проникновения в пласт фильтрата жидкости разрыва [127]. При проведении гидроразрыва в карбонатных коллекторах используются не только химически нейтральные жидкости, но и кислоты, растворяющие породу [137]. В последнем случае вокруг трещины может образоваться так называемая зона проникновения кислотного раствора, отличающаяся от остального пласта более высокой проницаемостью [159]. Задача о стационарном притоке к трещине бесконечной проводимости, расположенной внутри загрязненной зоны, характеризующейся пониженной проницаемостью, рассмотрена M. Prats [206]. Нестационарная фильтрация исследовалась H. Cinco-Ley, V.F. Samaniego [127], L.P. Roodhard, P.A. Fokker, D.R. Davies, J. Slyapobersky, G.K. Wong [215], D.W. Wong, A.B. Harrington, H. Cinco-Ley [248]. Расчеты показали, что наличие загрязненной зоны реального размера и проводимости практически не приводит к снижению эффективного радиуса скважины с трещиной гидроразрыва.
Модель трещинообразования в слоистом пласте, описывающая одновременное развитие серии трещин от различных интервалов перфорации, представлена в работе [114]. Особенности поведения скважин с трещинами гидроразрыва в слоистых пластах исследовались C.O. Bennett, R. Raghavan, A.C. Reynolds [115], R.G. Camacho, R. Raghavan, A.C. Reynolds [121], M.E. Osman [192], M.E. Osman, J.H. Abou-Kassem [193, 194], R.B. Sullivan, W.J. Lee, S.A. Holditch [232]. Рассматривалась неустановившаяся фильтрация слабосжимаемых жидкостей в слоистом пласте с разобщенными слоями, вскрытыми общим забоем. Предполагалось, что слои различаются по толщине hj, проницаемости kj, пористости фу и сжимаемости cj. Трещины гидроразрыва в каждом слое характеризуются своей длиной j раскрытием 2wj, проницаемостью kfj, пористостью фф сжимаемостью cfj и не сообщаются. Показано, что в неограниченном пласте доля дебита жидкости каждого слоя в начальный период времени определяется соответствующей по-лудлиной трещины, а на поздней стадии - проводимостью про-пластка [192]. В [193, 194] рассмотрена задача о притоке слабо-сжимаемой жидкости к скважине с вертикальной трещиной гидроразрыва, расположенной в центре прямоугольного слоистого пласта с непроницаемыми границами; предполагается, что трещина параллельна одной из границ пласта. Выделены четыре режима фильтрации, различающиеся характером зависимости забойного давления от времени: билинейный, линейный, псевдорадиальный и псевдостационарный. Продолжительность некоторых из этих периодов фильтрации может существенно сокращаться в зависимости от длины и проводимости трещины [193].
Для сопоставления течения в слоистом и в однослойном пластах в [115, 121] предлагается ввести эквивалентные полудлину 1 и проводимость 2kfw трещины:
2
n
l — SCRDjlj; j=1
n
U-
. J—1
CRD — S CRDj ; 2kfw —
j=1
2kfjw jhjC RDj
- kj - k
~; - j— ф—; - —^r~
RDj
- j ф jCjl фсц
фс — — S ф fjhj; h — S j k — — S kjhj.
Здесь j - номер пропластка, j — 1,n . Если в слоистом пласте создается единая трещина, а при расчете ее длины используются только усредненные параметры, то рассчитанная длина будет отличаться от реальной в CRD раз. В слоистом пласте целесообразно подбирать параметры трещин гидроразрыва для каждого слоя индивидуально. В случае двухслойного пласта максимум коэффициента продуктивности скважины достигается, если длины и проводимости трещин в каждом слое удовлетворяют условию
Cf2 h2 — CRD 21 . C — ^kfjW j
~ ; C f j ~“ *
Cf1 h1 C RDl\ k1j
2.5. ИССЛЕДОВАНИЯ ЭФФЕКТИВНОСТИ ГИДРОРАЗРЫВА В ГОРИЗОНТАЛЬНЫХ СКВАЖИНАХ
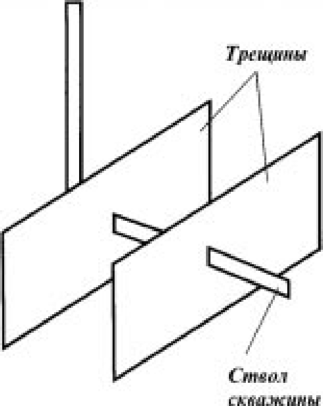
Исследованиям эффективности гидроразрыва в горизонтальных скважинах посвящены работы R. Raghavan, S.D. Joshi [209], M. Soliman, J.L. Hunt II, M. Azari [229], M. Soliman, J.L. Hunt II, W. El-Rabaa [230], R. Suprunowicz, R.M. Butler [233]. Если горизонтальная скважина пробурена параллельно направлению минимального горизонтального напряжения, то трещина гидроразрыва окажется ортогональна ее стволу (рис. 2.4). В такой ситуации особую актуальность имеет заканчивание трещины высокопрочным крупнозернистым проппантом и создание в прилегающей к забою части трещины высокопроницаемой зоны, так как при радиальном течении в трещине вблизи горизонтальной скважины существуют более высокие перепады давления, чем при плоскопараллельном течении вдоль трещины к вертикальной скважине.
В ограниченном пласте для трещин бесконечной проводимости при заданных свойствах пласта и жидкости с учетом естественной анизотропии можно найти оптимальное количество параллельных одинаковых трещин, ортогональных оси горизонтальной скважины, превышение которого не приводит к увеличению продуктив-
Рис. 2.4. Горизонтальная скважина, пересеченная трещинами гидроразрыва, перпендику
лярными ее стволу
ности скважины [229, 230]. В случае неограниченного пласта вклад трещин, пересекающих концевые участки горизонтального ствола, в суммарный дебит скважины значительно выше, чем вклад ближайших к центру трещин. Поэтому при наличии технологических возможностей в некоторых случаях целесообразно создание более длинных трещин гидроразрыва в удаленных частях ствола скважины. В ограниченном пласте трещины могут равномерно распределяться по площади дренирования. В работе [209] на основе принципа суперпозиции разработана процедура расчета эффективного радиуса горизонтальной скважины, пересеченной несколькими трансверсальными трещинами гидроразрыва, в предположении, что расстояния между трещинами превышают их длину, а приток из пласта осуществляется только через трещины.
Влияние вертикальных трещин, проходящих через горизонтальные скважины, на процесс конусообразования в водонефтяных и газонефтяных зонах исследовалось в [233], где, в частности, сопоставляются значения предельного безводного и безгазового дебита при различных конфигурациях системы “горизонтальная скважина - вертикальные трещины”. Показано, что вертикальная трещина, направленная вдоль оси горизонтальной скважины и простирающаяся в газовую шапку, приводит к стремительному загазовыванию скважины при работе на дебитах выше критического, однако значение предельного безгазового дебита в этом случае лишь незначительно ниже, чем для горизонтальной скважины при отсутствии трещины. Вертикальные трещины, перпендикулярные стволу скважины, увеличивают эффективную проницаемость системы как в вертикальном, так и в латеральном направлении, поэтому интенсифицируют фильтрацию нефти и газа или воды одновременно; при этом дебит нефти горизонтальной скважины, пересеченной трещинами, часто превышает дебит нефти горизонтальной скважины без трещин. В частности, может оказаться более высоким и предельный безгазовый дебит. Поскольку течение жидкости в окрестности горизонтальной скважины происходит не только в продольном, но и в вертикальном направлении, подчеркивается важность учета анизотропии при анализе фильтрационных процессов.
2.6. ОПТИМИЗАЦИЯ ПАРАМЕТРОВ ТРЕЩИН ГИДРОРАЗРЫВА
Проектирование гидроразрыва с целью достижения максимальной производительности скважин требует специального изучения влияния различных параметров трещины и пластовой системы на величину дебита. Как было показано выше, увеличение длины или проводимости трещины, а следовательно, и затрат на проведение гидроразрыва не приводит к пропорциональному возрастанию дебита скважины. Учитывая конечную проницаемость трещины, можно определить предельную длину, превышение которой практически не приводит к приросту дебита [37, 43]. Для трещины фиксированной длины увеличение ее раскрытия или проницаемости при превышении некоторых значений проводимости также дает незначительный эффект [137]. Вопросы оптимизации размеров и проводимости одиночной трещины рассмотрены C.O. Bennett, N.D. Rosato, A.C. Reynolds, R. Raghavan [117], M.J. Eco-nomides, K.G. Nolte [137], J.L. Elbel [140, 141], S.A. Holditch, J.W. Jennings, S.H. Neuse, R.E. Wyman [160], R.A. Morse, W.D. Von Gon-ten [183], M. Prats [206]. При фиксированном объеме трещины, определяемом расходом проппанта, и при прочих равных условиях максимальная накопленная добыча жидкости при установившейся фильтрации достигается при безразмерной проводимости CfD = = 2kfw/krl = 1,26 [206]. Этот критерий справедлив для средне- и высокопроницаемых пластов (kr > 0,001 мкм2). В низкопроницаемых пластах продолжительность периода неустановившегося притока, в течение которого приведенный критерий неприменим, составляет несколько лет. Расчеты показали, что для пластов с проницаемостью от 10-6 до 10-4 мкм2 оптимальное значение безразмерной проводимости составляет CfD = 3 [140]. При фиксированных объеме и длине трещины сильное влияние на коэффициент продуктивности имеет распределение проницаемости упаковки проппанта вдоль трещины [171]. Как уже было указано [117], дебит скважины после гидроразрыва в начальный период времени определяется проводимостью ближайшей к забою части трещины, а по прошествии длительного периода - средним арифметическим значений проводимости вдоль трещины.
Другими факторами, определяющими выбор оптимальных размеров трещин гидроразрыва, являются расположение скважин и ориентация трещин относительно сетки скважин [137, 141, 160, 169, 172, 178]. На основе простых аналитических моделей определяются оптимальные соотношения между размерами неравномерной прямоугольной сетки размещения скважин и длиной трещин гидроразрыва при условии, что трещины параллельны одной из линий сетки скважин. При неизменной площади области дренирования скважины изменение формы этой области, т.е. соотношения сторон прямоугольника, позволяет увеличить накопленную добычу жидкости (рис. 2.5). В случае квадратной сетки скважин эффективны более короткие трещины, чем в случае прямоугольной сетки. При прямоугольной сетке скважин выгодно направление трещин вдоль большей стороны прямоугольника. Чем больше различаются расстояния между скважинами в двух взаимно ортогональных направлениях и чем больше длина трещин, тем выше темп отбора жидкости. Знание ориентации трещин особенно актуально при создании протяженных трещин, когда длина трещины приближается к расстоянию между скважинами, а также при заводнении пластов, когда при неблагоприятной ориентации трещин возможны преждевременные прорывы воды в добывающие скважины [169].
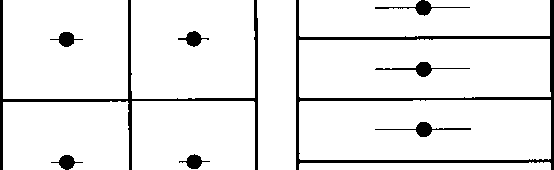
Рис. 2.5. Схемы расположения скважин с трещинами гидроразрыва:
1 - скважина; 2 - трещина
Влияние неоднородности пласта на оптимизацию длины трещин и расположения скважин рассматривалось D.N. Meehan [178] на основе условного моделирования. Неизвестное случайное поле проницаемости строилось с учетом всех достоверно известных точек. При этом воспроизводились как среднее значение проницаемости, так и ковариационная функция. Показано, что масштаб неоднородности, радиус корреляции и анизотропия проницаемости определяют фильтрационные потоки в пласте с трещиной гидроразрыва. Если радиус корреляции проницаемости меньше четверти длины трещины, то фильтрационное поле ведет себя как однородное. При высокой степени неоднородности фильтрационные потоки зависят от конкретной реализации поля проницаемости, а не от его статистических характеристик. Особенно важен радиус корреляции неоднородности в направлении трещины. Если радиус корреляции неоднородности в направлении трещины велик по сравнению с длиной трещины, то корреляция в ортогональном направлении несущественна.
При оптимизации гидроразрыва необходим комплексный подход, когда помимо фильтрационных свойств пласта и трещины учитываются технические и технологические ограничения на давление разрыва, вязкость жидкости, концентрацию проппанта и т.п. Учет многих параметров и выбор допустимых значений при оптимизации гидроразрыва может быть осуществлен с использованием аппарата теории нечетких множеств [111]. Решающим при 62 выборе технологии и параметров трещины является техникоэкономический анализ, учитывающий разнообразные факторы и направленный на максимизацию производительности скважины при минимизации затрат на проведение гидроразрыва [137, 143, 147, 171, 242]. В результате определяется экономический оптимум длины трещины. Наиболее высокую экономическую эффективность дает сочетание передовых технологий гидроразрыва с предварительным и последующим анализом производительности скважины, использованием трехмерного моделирования процесса трещинообразования и проведением расчетов в реальном времени с целью корректировки параметров гидроразрыва.
2.7. ИССЛЕДОВАНИЯ ИНТЕРФЕРЕНЦИИ СКВАЖИН, ПЕРЕСЕЧЕННЫХ ТРЕЩИНАМИ ГИДРОРАЗРЫВА
При комплексном подходе к проектированию гидроразрыва пласта среди прочих факторов необходимо учитывать интерференцию скважин. Если взаимодействуют две скважины и отношение длины трещины, созданной на одной из них, к расстоянию между ними больше некоторой критической величины, то производительность скважин зависит также и от ориентации трещины. Достаточно простые методы определения ориентации трещин, основанные на тестах по интерференции, когда наблюдения за неуста-новившимися фильтрационными процессами ведутся в соседних пьезометрических скважинах, предложены L.F. Elkins, A.M. Skov [142], N.A. Mousli, R. Raghavan, H. Cinco-Ley, V.F. Samaniego [184], A. Uraiet, R. Raghavan, G.W. Thomas [240]. На основе известных решений [126, 128, 152] рассчитывается распределение давления в неограниченном однородном пласте при остановке или включении скважины, пересеченной вертикальной трещиной. По известному расстоянию между активной скважиной и скважиной-наблюдателем определяется динамика пластового давления в соответствующей точке при различной ориентации трещины и сопоставляется с наблюдаемыми значениями. Ориентация трещины оценивается по зависимости, дающей наилучшее совпадение с фактическими результатами. Если отношение расстояния между скважинами к полной длине трещины не более 2, то наличие трещины и ее азимут оказывают существенное влияние на поведение давления. При фиксированном расстоянии между скважинами, если угол между прямой, соединяющей скважины, и осью трещины более 45°, то давление в скважине-наблюдателе слабо чувствительно к величине этого угла. Особенности исследования интерференции в протяженных линейных системах, когда все течение в пласте направлено вдоль линии, соединяющей скважины, рассмотрены в работах [139, 244].
Интерференция скважин в пласте при массовом проведении гидравлического разрыва изучалась И.М. Муравьевым, Го Шан-пин [73] для упругого и жестководонапорного режимов фильтрации методом фильтрационных сопротивлений. Рассматривалась полосообразная залежь с рядной системой расстановки скважин. Показано, что увеличение дебитов рядов эксплуатационных скважин, в которых проводился разрыв, всегда сопровождается снижением дебитов остальных эксплуатационных рядов, а разрыв пласта в нагнетательных скважинах вызывает рост дебитов из всех эксплуатационных скважин. Гидроразрывом только в эксплуатационных скважинах нельзя добиться значительного прироста добычи жидкости без интенсификации нагнетательных скважин.
Влияние интерференции скважин на эффективность гидроразрыва при периодических площадных и рядных системах расстановки добывающих и нагнетательных скважин изучалось В.М. Ентовым, В.В. Мурзенко [28], В.В. Мурзенко [74]. Рассматривалась стационарная однофазная фильтрация в элементах параллельной, пяти- и девятиточечной систем расстановки скважин. В случае трещин бесконечной проводимости решение задачи было получено методом конформных отображений, особенности поведения решения при конечной проводимости трещин исследовались численно методом конечных элементов. Показано, что при стационарной однофазной фильтрации эффекты, связанные с ориентацией трещин, малы. Отмечено существенное увеличение коэффициента продуктивности эксплуатационных скважин в случае, когда трещины созданы во всех скважинах, по сравнению со случаем, когда они созданы только в добывающих или только в нагнетательных скважинах.
2.8. ЧИСЛЕННЫЕ МОДЕЛИ ФИЛЬТРАЦИИ В ПЛАСТЕ С ТРЕЩИНАМИ ГИДРОРАЗРЫВА
Только детальный гидродинамический анализ и математическое моделирование участка пласта или объекта в целом позволяют проанализировать влияние распределения неоднородности пласта и интерференции скважин, определить параметры и оптимальное размещение гидроразрывов на объекте. Наиболее высокая эффективность гидроразрыва может быть достигнута при проектировании его применения как элемента системы разработки с учетом системы размещения скважин и оценкой их взаимовлияния при различных сочетаниях обработки добывающих и нагнетательных скважин.
В общем случае анализ сложных двух- или трехмерных многофазных течений в системе скважин с трещинами гидроразрыва возможен только на основе численного моделирования [2, 59, 67, 89], позволяющего учесть особенности строения объекта [19, 96], свойства жидкостей, расстановку скважин, направление трещин и т.п.
Одновременное моделирование течения в пласте и в трещине конечно-разностными методами сопряжено с большими сложностями (вычислительными и методическими), связанными с необходимостью введения расчетных ячеек, размеры которых различаются на несколько порядков, и использованием мелких временных шагов. Поэтому подход с одновременным моделированием течения в пласте и в трещине при помощи конечно-разностных алгоритмов обычно применяется при решении задач, которые ставятся для отдельно взятой скважины, например для расчета фильтрации и утечек в пласт жидкости разрыва при моделировании возникновения и распространения трещины [218, 219, 221] или для идентификации параметров пласта и трещины по данным неустановившейся фильтрации [106, 162, 170]. При этом фильтрация в пласте полагается двух- или трехмерной. Трещина считается прямоугольной, течение в трещине одномерное, обмен жидкостью между пластом и трещиной осуществляется только через боковые поверхности. Трещина ориентирована вдоль одной из осей разностной сетки и представлена рядом ячеек малой ширины, высокой проницаемости и пористости. В окрестности скважины и трещины необходимо измельчение разностной сетки. Как уже указывалось, такие модели могут использоваться как составная часть комплексной модели возникновения и развития трещины и недостаточно эффективны при моделировании процессов разработки месторождений, когда требуется расчет сложных фильтрационных течений в системе скважин с трещинами гидроразрыва.
Альтернативными являются полностью расщепленные модели, в которых раздельно рассматриваются трещина и пласт. В модели, рассчитывающей геометрию трещины и перенос проппанта, фильтрацию в пласт учитывают упрощенно, путем введения коэффициента утечек. Для пласта используют обычные фильтрационные модели, в которых эффекты, связанные с наличием трещины, учитываются косвенно, путем модификации каких-либо свойств пласта, приписываемых расчетным блокам, содержащим трещину. Причем эти изменения, как правило, вносятся в фильтрационную модель вручную. В частности, распространен подход, когда для скважин с трещинами гидроразрыва задают увеличенный радиус или коэффициент продуктивности. Следует отметить, что этот подход дает удовлетворительные результаты только в случае, когда трещина гидроразрыва содержится внутри одной расчетной ячейки.
A. Settari, R.C. Bachman, K.A. Hovern, S.G. Paulsen [220], A. Settari, Y. Ito, K.N. Jha [222], A. Settari, P.J. Puchir, R.C. Bachman [223] предлагают частичное расщепление моделей пласта и трещины. При этом разностные сетки для пласта и для трещины независимы, а дополнительный модуль - специальный интерфейс -осуществляет “стыковку” моделей, пересчитывая модифицированные параметры скважин и расчетных блоков, внутри которых расположена трещина. В модели пласта трещина не моделируется отдельными расчетными блоками. Важными преимуществами применения независимых разностных сеток являются возможность использования достаточно крупной разностной сетки в модели пласта и более высокая чувствительность модели при расчете процесса роста трещины. При этом повышается вычислительная эффективность программ и снижается требуемый объем памяти. В результате расчета параметров трещины вычисляются проводимости блоков для сеточной модели трещины Ti!im. Предполагается, что трещина направлена вдоль оси x. Затем вычисляется общая проводимость трещины между блоками i и i + 1 модели пласта:
Здесь суммирование производится по всем блокам трещины, расположенным между i и i + 1. Результирующая проводимость вдоль направления трещины Tttto,5 определяется в результате суммирования собственной проводимости пласта T'xii+0 5 и проводимости трещины:
T r f
TT = T . + Tf
^XJH-O5 JXJF05 -LX2b05 *
Для учета в модели пласта зоны проникновения фильтрата жидкости разрыва аналогично модифицируются проводимости в направлении оси y. При моделировании многофазной фильтрации вводятся фазовые проницаемости для пласта krI и для трещины krf, которые зависят от соответствующих насыщенностей S/ и Sj^. Здесь индекс 1 обозначает фазу: нефть, воду или газ. Обычно принимается, что в трещине фазовая проницаемость пропорциональна соответствующей насыщенности. Предполагается, что насыщенности в трещине в добывающей скважине равны насыщенностям в соответствующем блоке расчетной модели пласта, а трещина в нагнетательной скважине заполнена закачиваемым флюидом. В модели пласта для блоков, через которые проходит трещина, вводятся псевдофункции фазовых проницаемостей
k = Txkrz(Sl) + TxkHf(Slf)
Kl= tt .
1 X
Представленный подход использовался, в частности, для исследования производительности газоконденсатных скважин с трещинами гидроразрыва [220]. Показано, что гидроразрыв - эффективное средство для восстановления продуктивности скважин, призабойная зона которых заблокирована конденсатом. В низкопроницаемых пластах длина трещины является более значимым параметром для максимизации коэффициента продуктивности, чем проводимость. В пластах более высокой проницаемости создание трещин длиной свыше 80-100 м нецелесообразно, при этом существенным фактором становится увеличение проводимости трещины. Повышение степени неоднородности пласта снижает относительную выгоду от проведения гидроразрыва. Значительное снижение коэффициента продуктивности скважины после гидроразрыва может явиться результатом турбулизации потока газа в трещине, особенно в условиях селективной перфорации.
Другая разновидность частично расщепленных моделей, основанная на моделировании трещины гидроразрыва как совокупности точечных источников (стоков), находящихся в расчетных ячейках, через которые проходит трещина, предложена L.X. Nghiem [188], L.X. Nghiem, P.A. Forsyth Jr., A. Behie [189]. Интенсивности этих источников определяются при помощи специальных формул притока, что в конечном счете сводится к подбору или аналитическим оценкам коэффициентов продуктивности, которые впоследствии вводятся в традиционные численные модели фильтрации. В работе [188] получены такие формулы притока в предположении, что трещина идеальная, т.е. имеет бесконечную проводимость, а давление вдоль трещины постоянно. Поток внутрь или из трещины для каждого разностного блока, содержащего трещину, рассчитывается через разность давлений в трещине и в блоках, окружающих данный. Метод источников широко используется при численном моделировании месторождений для представления скважин, например, в работах D.W. Peaceman [198200]. Дискретизация уравнений осуществляется так, как если бы источника (стока) не было. Вклад этого источника потом добавляется с учетом типа фильтрации, связанного с ним (линейная, радиальная, эллиптическая и т.д.). При моделировании трещины для каждого блока, пересекаемого ею, вычисляется поток, который втекает или вытекает из содержащейся внутри блока части трещины:
Pf - Pe
ln[(ae + be )/1
i
kh qx1x2 = —2 Xi 2 ц
Здесь предполагается, что трещина направлена вдоль оси x, x12 - расстояние от центра трещины до границ блока; pj - давление на контуре эллипса с полуосями ae и be, конфокального трещине. В случае многофазной фильтрации общий поток и давления вычисляются через суммарную подвижность фаз, которая определяется как среднее гармоническое суммарных подвижностей в соседних блоках. Фазовые потоки выражаются через отношение фазовой
подвижности к суммарной. Модель также позволяет учитывать скин-эффект, обусловленный загрязненной зоной, контур которой конфокален контуру трещины.
Накопленный за 50 лет опыт проведения гидравлического разрыва пласта и развитие теоретических представлений об этом процессе позволили значительно усовершенствовать его технологию [41, 83, 84, 137, 147, 171, 217]. Наряду с созданием новых материалов для гидроразрыва пласта, разработкой новых методов его проведения, актуальной стала проблема комплексного подхода к оценке эффективности гидроразрыва с учетом его влияния не только на производительность отдельной скважины, но и на процесс разработки месторождения в целом. Несмотря на огромное количество исследований фильтрации в пласте с трещинами гидроразрыва, эта проблема далека от своего окончательного решения.
Недостаточно изучены влияние гидроразрыва на добычу углеводородов из неоднородных коллекторов; особенности многофазной фильтрации в окрестности трещин гидроразрыва; влияние ориентации трещин гидроразрыва на продвижение водо- и газонефтяного контакта, а также закачиваемой в пласт воды. Появление новых разновидностей технологии гидравлического разрыва пласта, например таких, как импульсный гидроразрыв, гидроразрыв в горизонтальных скважинах и других, требует создания новых расчетных моделей фильтрации.
Внедрение комплексного подхода к проектированию гидроразрыва пласта, основанного на учете разнообразных факторов, таких как проводимость пласта, система расстановки скважин, механика трещины, характеристики жидкости разрыва и проппанта, технологические и экономические ограничения, привело к тому, что наряду с моделями трещинообразования возникла необходимость создания моделей фильтрации в системе скважин с трещинами гидроразрыва.
eAaNOa aAaOUa lEaOQeNeeeNeQ Qieeea q eeaeeNgea eeeieOgaa
